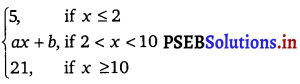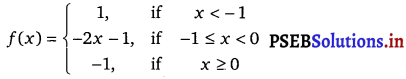Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.1 Textook Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.1
Question 1.
Prove that the function f(x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.
Solution.
The given functions is f(x) = 5x – 3
At x = 0, f(0) = 5 × 0 – 3 = – 3
\(\lim _{x \rightarrow 0}\) f(x) = \(\lim _{x \rightarrow 0}\) (5x – 3)
= 5 × 0 – 3 = -3
∴ \(\lim _{x \rightarrow 0}\) f(x) = f(0)
Therefore, f is continuous at x = 0.
At x = – 3, f(- 3) = 5 × (- 3) – 3 = -18
\(\lim _{x \rightarrow-3}\) f(x) = \(\lim _{x \rightarrow-3}\) (5x – 3)
= 5 × (- 3) – 3 = – 18
∴ \(\lim _{x \rightarrow-3}\) f(x) = f(- 3)
Therefore, f is continuous at x = – 3.
At x = 5, f(x) = f(5) = 5 × 5 – 3
= 25 – 3 = 22
\(\lim _{x \rightarrow 5}\) f(x) = \(\lim _{x \rightarrow 5}\) (5x – 3)
= 5 × 5 – 3 = 22
\(\lim _{x \rightarrow 5}\) f(x) = f(5)
Therefore, f is continuous at x = 5.

Question 2.
Examine the continuity of the function f(x) = 2x2 – 1 at x = 3.
Solution.
The given functions is f(x) = 2x2 – 1
At x = 3, f(3) = 2 × 32 – 1 = 17
\(\lim _{x \rightarrow 3}\) f(x) = \(\lim _{x \rightarrow 3}\) (2x2 – 1)
= 2 × 32 – 1 = 17
∴ \(\lim _{x \rightarrow 3}\) f(x) = f(3)
Thus, f is continuous at x = 3.

Question 3.
Examine the following functions for continuity.
(a) f(x) = x – 5
(b) f(x) = \(\frac{1}{x-5}\) x ≠ 5
(c) f(x) = \(\frac{x^{2}-25}{x+5}\)
(d) f(x) = |x – 5|
Sol.
(a) The given function is f(x) = x – 5
x – 5 is a polynomial, therefore it is continuous at each x ∈ R.
(b) The given function is f(x) = \(\frac{1}{x-5}\)
At x = 5, f(x) is not defined.
when x ≠ 5, \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) \(\frac{1}{x-5}=\frac{1}{c-5}\)
∴ f is not continuous at x = 5.
∴ f is continuous at x ∈ R – {5}.
(c) The given function is f(x) = \(\frac{x^{2}-25}{x+5}\)
At x = – 5, function f is not defined.
∴ f is discontinuous at x = – 5.
At x = c ≠ – 5
\(\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c} \frac{x^{2}-25}{x+5}\) = x – 5
and f(c) = c – 5
∴ f is continuous for all x ∈ R – {- 5}
(d) The given function is f(x) = |x – 5|
At x = 5, f(5) = |5 – 5| = 0
\(\lim _{x \rightarrow 5}\) |x – 5| = 0
∴ f is continuous at x = 5
At x = c > 5, \(\lim _{x \rightarrow c}\) |x – 5| = c – 5 [c > 5]
Also, f(c) = c – 5
∴ f is continuous at x = c > 5.
Similarly at x = c < 5
\(\lim _{x \rightarrow c}\) |x – 5| = 5 – c, f(c) = 5 – c
∴ f is continuous at x = c < 5
Thus, f is continuous for all x ∈ R.

Question 4.
Prove that the function f(x) = xn is continuous at x – n, where n is a positive integer.
Solution.
The given function is f(x) = xn.
It is evident that / is defined at all positive integers n, and its value at n is nn.
Then, \(\lim _{x \rightarrow n}\) f(n) = \(\lim _{x \rightarrow n}\) (xn) = nn
\(\lim _{x \rightarrow n}\) f(x) = f(n)
Therefore, f is continuous at n, where n is a positive integer.

Question 5.
Is the function f defined by f(x) =  continuous at x = 0? At x = 1? At x = 2?
continuous at x = 0? At x = 1? At x = 2?
Solution.
The given function f is f(x) = 
At x = 0, it is evident that f is defined at 0 and its value at 0 is 0.
Then, \(\lim _{x \rightarrow 0}\) f(x) = \(\lim _{x \rightarrow 0}\) x = 0
∴ \(\lim _{x \rightarrow 0}\) f(x) = f(0)
Therefore, f is continuous at x = 0.
At x = 1, f is defined at 1 and its value at 1 is 1.
The left hand limit of f at x = 1 is lim f(x) lim x – 1
\(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) x = 1
The right hand limit of f at x = 1 is
\(\lim _{x \rightarrow 1^{+}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) (5) = 5.
∴ \(\lim _{x \rightarrow 1^{-}}\) f(x) ≠ \(\lim _{x \rightarrow 1^{+}}\) f(x)
Therefore, f is not continuous at x = 1.
At x = 2, f is defined at 2 and its value at 2 is 5.
Then, \(\lim _{x \rightarrow 2}\) f(x) = \(\lim _{x \rightarrow 2}\) (5) = 5 ‘
∴ \(\lim _{x \rightarrow 2}\) f(x) = f(2)
Therefore, f is continuous at x = 2.

Direction (6 – 12): Find all points of discontinuity of f, where f is defined by
Question 6.
f(x) = 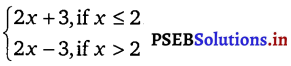
Solution.
The given function is f(x) = 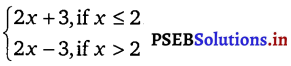
It is evident that the given function f is defined at all the points of the real line.
Let c be a point on the real line. Then, three cases arise.
I. c < 2; II. c > 2;
III. c = 2
Case I. c < 2
Then, f(c) = 2c + 3
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (2x + 3) = 2c +3
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < 2. Case II. c > 2
Then, f(c) = 2c – 3
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (2x – 3) = 2c – 3
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 2.
Case III. c = 2
Then, the left hand limit of f at x = 2 is
\(\lim _{x \rightarrow 2^{-}}\) f(x) = \(\lim _{x \rightarrow 2^{-}}\) (2x + 3)
= 2 × 2 + 3 = 7
The right hand limit of f at x = 2 is
\(\lim _{x \rightarrow 2^{+}}\) f(x) = \(\lim _{x \rightarrow 2^{+}}\) (2x – 3)
= 2 × 2 – 3 = 1
It is observed that the left and right hand limits of f at x = 2 do not coincide.
Therefore, f is not continuous at x = 2.
Hence, x = 2 is the only point of discontinuity of f.

Question 7.
f(x) = 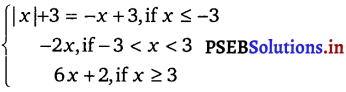
Solution.
The given function is f(x) = 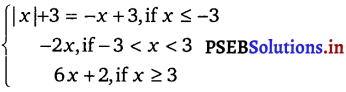
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
If c < – 3, then f(c) = – c + 3
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (- x + 3) = – c + 3
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < – 3.
Case II:
If c = – 3, then f(- 3) = – (- 3) + 3 = 6
\(\lim _{x \rightarrow-3^{-}}\) f(x) = \(\lim _{x \rightarrow-3^{-}}\) (- x + 3)
= – (- 3) + 3 = 6
\(\lim _{x \rightarrow-3^{+}}\) f(x) = \(\lim _{x \rightarrow-3^{+}}\) (- 2x)
= – 2 × (- 3) = 6
∴ \(\lim _{x \rightarrow-3}\) f(x) = f(- 3)
Therefore, f is continuous at x = – 3.
Case III:
If – 3 < c < 3, then f(c) – 2c and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (- 2x) = – 2c \(\lim _{x \rightarrow c}\) f(x) = f(c) Therefore, f is continuous in (- 3, 3).
Case IV:
If c = 3, then the left hand limit of f at x = 3 is \(\lim _{x \rightarrow 3^{-}}\) f(x) = \(\lim _{x \rightarrow 3^{-}}\) (- 2x) = – 2 × 3 = – 6
The right hand limit of f at x = 3 is \(\lim _{x \rightarrow 3^{+}}\) f(x) = \(\lim _{x \rightarrow 3^{+}}\) (6x + 2) = 6 × 3 + 2 = 20
It is observed that the left and right hand limits of f at x = 3 do not coincide.
Therefore, f is not continuous at x = 3.
Case V:
If c > 3, then f(c) = 6c + 2 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (6x + 2) = 6c + 2
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 3.
Hence, x = 3 is the only point of discontinuity of f.

Question 8.
f(x) = 
Solution.
The given function is f(x) = 
It is known that, x < 0 ⇒ |x| = – x and x > 0
⇒ |x| = x
Therefore, the given function can be rewritten as
f(x) = 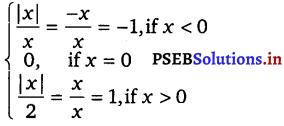
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
If c < 0, then f(c) = – 1
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (- 1) = – 1
⇒ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < 0.
Case II:
If c = 0, then
the left hand limit of f at x = 0 is \(\lim _{x \rightarrow 0^{-}}\) f(x) = \(\lim _{x \rightarrow 0^{-}}\) (- 1) = – 1
The right hand limit of f at x = 0 is \(\lim _{x \rightarrow 0^{+}}\) f(x) = \(\lim _{x \rightarrow 0^{+}}\) (1) = 1
It is observed that the left and right hand limits of f at x = 0 do not coincide.
Therefore, f is not continuous at x = 0.
Case III: If c > 0, then f(c) = 1
\(\lim _{x \rightarrow 0^{-}}\) f(x) = \(\lim _{x \rightarrow 0^{-}}\) (1) = 1
∴ \(\lim _{x \rightarrow 0^{-}}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 0.
Hence, x = 0 is the only point of discontinuity of f.

Question 9.
f(x) = 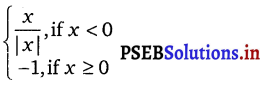
Solution.
The given function is f(x) = 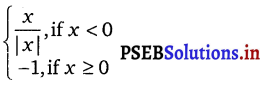
It is known that, x < 0 ⇒ |x| = – x
Therefore, the given function can be written as
f(x) = 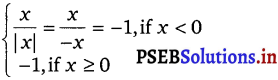
⇒ f(x) = – 1 for all x ∈ R
Let c be any real number.
Then, \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (- 1) = – 1
Also, f(c) = – 1 = \(\lim _{x \rightarrow c}\) f(x)
Therefore, the given function is a continuous function.
Hence, the given function has no point of discontinuity.

Question 10.
f(x) = 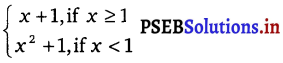
Solution.
The given function is f(x) = 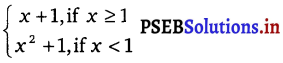
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
If c < 1, then f(c) = c2 + 1 and lim f(x) = lim(x2 + 1) = c2 + 1
X ~+ c x->c
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < 1.
Case II:
If c = 1, then f(c) = f(1) = 1 + 1 = 2.
The left hand limit of f at x = 1 is
\(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (x2 + 1)
= 12 + 1 = 2
The right hand limit of f at x = 1 is
\(\lim _{x \rightarrow 1^{+}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) (x + 1)
= 1 + 1 = 2
∴ \(\lim _{x \rightarrow c}\) f(x) = f(1)
Therefore, f is continuous at x = 1
Case III:
If c > 1, then f(c) = c + 1
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x +1) = c + 1
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 1.
Hence, the given function f has no point of discontinuity.

Question 11.
f(x) = 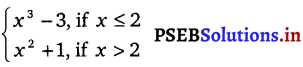
Solution.
The given function is f(x) = 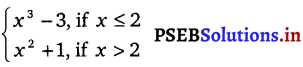
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
If c < 2, then f(c) = c3 – 3 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x3 – 3) = c3 – 3
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < 2.
Case II:
If c = 2, then f(c) = f(2) = 23 – 3 = 5
\(\lim _{x \rightarrow 2^{-}}\) f(x) = \(\lim _{x \rightarrow 2^{-}}\) (x3 – 3)
= 23 – 3 = 5
\(\lim _{x \rightarrow 2^{+}}\) f(x) = \(\lim _{x \rightarrow 2^{+}}\) (x2 + 1)
= 22 + 1 = 5
∴ \(\lim _{x \rightarrow 2}\) f(x) = f(2)
Therefore, f is continuous at x = 2.
Case III:
If c > 2, then f(c) = c2 + 1
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x2 + 1) = c2 + 1
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 2.
Thus, the given function f is continuous at every point on the real line.
Hence, f has no point of discontinuity.

Question 12.
f(x) = 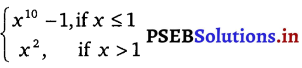
Solution.
The given function f is f(x) = 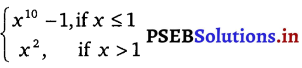
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
If c < 1, then f(c) = c10 – 1 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x10 – 1) = c10 – 1
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < 1.
Case II:
If c = 1, then the left hand limit of f at x = 1 is
\(\lim _{x \rightarrow 1^{-}}\) (x) = \(\lim _{x \rightarrow 1^{-}}\) (x10 – 1)
= 110 – 1 = 1 – 1 = 0
The right hand limit of f at x = 1 is
\(\lim _{x \rightarrow 1^{+}}\) (x) = \(\lim _{x \rightarrow 1^{+}}\) (x2)
= 12 = 1
It is observed that the left and right hand limit of f at x = 1 do not coincide.
Therefore, f is not continuous at x = 1.
Case III:
If c > 1, then f(c) = c2
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x2) = c2
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 1.
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.

Question 13.
Is the function defined by
f(x) = 
a continuous function?
Solution.
The given function f is 
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
If c < 1, then f(c) = c + 5 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x + 5) = c + 5
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < 1.
Case II:
If c = 1, then f(1) = 1 + 5 = 6
The left hand limit of f at x = 1 is \(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (x + 5) = 1 + 5 = 6
The right hand limit of f at x = 1 is \(\lim _{x \rightarrow 1^{+}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) (x – 5) = 1 – 5 = – 4
It is observed that the left and right hand limits of f at x = 1 do not coincide. Therefore, f is not continuous at x = 1.
Case III:
If c > 1, then f(c) = c – 5 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x – 5) = c – 5
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 1.
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.

Direction (14 – 16) : Discuss the continuity of the function f, where f is defined by
Question 14.
f(x) = 
Solution.
The given function is 
The given function is defined at all points of the interval [0, 10].
Let c be a point in the interval [0, 10].
Case I:
If 0 < c < 1, then f(c) = 3 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (3) = 3
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous in the interval (0, 1).
Case II:
If c = 1, then f(3) = 3
The left hand limit of f at x – 1 is
\(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (3) = 3
The right hand limit of f at x = 1 is
\(\lim _{x \rightarrow 1^{+}}\) f(x) \(\lim _{x \rightarrow 1^{
+}}\) (4) = 4
It is observed that the left and right hand limits of f at x -1 do not coincide.
Therefore, f is not continuous at x = 1.
Case III:
If 1 < c < 3, then f(c) = 4 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) f(4) = 4
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points of the interval (1, 3).
Case IV:
If c = 3, then /(c) = 5
The left hand limit of / at x = 3 is
\(\lim _{x \rightarrow 3^{-}}\) f(x) = \(\lim _{x \rightarrow 3^{-}}\) (4) = 4
The right hand limit of / at x = 3 is
\(\lim _{x \rightarrow 3^{+}}\) f(x) = \(\lim _{x \rightarrow 3^{+}}\) (5) = 5
It is observed that the left and right hand limits of f at x = 3 do not coincide.
Therefore, f is not continuous at x = 3.
Case V:
If 3 < c ≤ 10, then f(c) = 5 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (5) = 5
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points of the interval (3, 10).
Hence, f is not continuous at x = 1 and x = 3.

Question 15.
f(x) = 
Solution.
The given function is f(x) = 
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
If c < 0, then f(c) = 2c
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (2x) = 2c
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Case II:
If c = 0, then f(c) = f(0) = 0
The left hand limit of f at x = 0 is
\(\lim _{x \rightarrow 0^{-}}\) f(x) = \(\lim _{x \rightarrow 0^{-}}\) (2x)
= 2 × 0 = 0
The right hand limit of f at x = 0 is
\(\lim _{x \rightarrow 0^{+}}\) f(x) = \(\lim _{x \rightarrow 0^{+}}\) f(0) = 0
∴ \(\lim _{x \rightarrow 0}\) f(x) = f(0)
Therefore, f is continuous at x = 0.
Case III:
If 0 < c < 1, then f(x) = 0 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (0) = 0
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points of the interval (0, 1).
Case IV:
If c = 1, then f(c) = f(1) = 0
The left hand limit of f at x = 1 is
\(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (0) = 0
The right hand limit of f at x = 1 is
\(\lim _{x \rightarrow 1^{+}}\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) (4x) = 4 × 1 = 4
It is observed that the left and right hand limits of f at x = 1 do not coincide.
Therefore, f is not continuous at x = 1.
Case V:
If c < 1, then f(c) = 4c and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (4x) = 4c ∴ \(\lim _{x \rightarrow c}\) f(x) = f(c) Therefore, f is continuous at all points x, such that x > 1.
Hence, f is continuous only at x = 1.

Question 16.
f(x) = 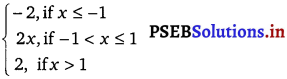
Solution.
The given function is f(x) = 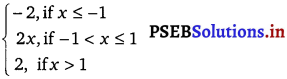
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
If c < – 1, then f(c) = – 2 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) f(- 2) = – 2
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < – 1.
Case II:
If c = – 1, then f(c) = f(- 1) = – 2
The left hand limit of f at x = – 1 is
\(\lim _{x \rightarrow-1^{-}}\) f(x) =\(\lim _{x \rightarrow-1^{-}}\) (- 2) = – 2
The right hand limit of f at x = – 1 is
\(\lim _{x \rightarrow-1^{+}}\) f(x) = \(\lim _{x \rightarrow-1^{+}}\) (2x)
= 2 × (- 1) = – 2
∴ \(\lim _{x \rightarrow-1}\) f(x) = f(- 1)
Therefore, f is continuous at x = – 1.
Case III:
If – 1 < c < 1, then f(c) = 2c \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (2x) = 2c ∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points of the interval (- 1, 1).
Case IV:
If c = 1, then f(c) = f(1) = 2 x 1 = 2.
The left hand limit of f at x = 1 is \(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (2x) = 2 x 1 = 2
The right hand limit of f at x = 1 is \(\) f(x) = \(\lim _{x \rightarrow 1^{+}}\) 2 = 2
⇒ \(\lim _{x \rightarrow 1}\) f(x) = f(c)
Therefore, f is continuous at x = 2.
Case V:
If c > 1, then f(c) = 2 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (2) = 2
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 1.
Thus, from the above observations, it can be concluded that f is continuous at all points of the real line.

Question 17.
Find the relationship between a and b so that the function f defined by f(x) = 
is continuous at x = 3.
Solution.
The given function is f(x) = 
If f is continuous at x = 3, then
\(\lim _{x \rightarrow 3^{-}}\) f(x) = \(\lim _{x \rightarrow 3^{-}}\) f(x) = f(3) ……… (i)
\(\lim _{x \rightarrow 3^{-}}\) f(x) = \(\lim _{x \rightarrow 3^{-}}\) (ax + 1) = 3a + 1
\(\lim _{x \rightarrow 3^{+}}\) f(x) = \(\lim _{x \rightarrow 3^{+}}\) (bx + 3) = 3b + 3
Therefore, from Eq. (i), we get
3a + 1 = 3b + 3
⇒ 3a = 3b + 2
⇒ a = b + \(\frac{2}{3}\)
Therefore, the required relationship is given by, a = b + \(\frac{2}{3}\).
Question 18.
For what value of λ, is the function defined by
f(x) = 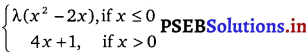
continuous at x = 0 ? What about continuity at x = 1 ?
Solution.
The given finction is f(x) = 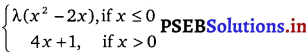
If f is continuous at x = 0, then
\(\lim _{x \rightarrow 0^{-}}\) f{x) = \(\lim _{x \rightarrow 0^{+}}\) f(x) = f(0)
⇒ \(\lim _{x \rightarrow 0^{-}}\) (x2 – 2x) = \(\lim _{x \rightarrow 0^{+}}\) (4x + 1)
= λ (02 – 2 × 0)
⇒ λ (02 – 2 × 0) = 4 × 0 + 1 = 0
⇒ 0 = 1 = 0, which is not possible.
Therefore, there is no value of λ, for which f is continuous at x = 0.
At x = 1,
f(x) = 4x + 1 = 4 x 1 + 1 = 5
\(\lim _{x \rightarrow 1}\) (4x + 1) = 4 x 1 + 1 = 5
∴ \(\lim _{x \rightarrow 1}\) f(x) = f(1)
Therefore, for any values of λ, f is continuous at x = 1.

Question 19.
Show that the function defined by g(x) = x – [x] is discontinuous at all integral points. Here, [x] denotes the greatest integer less than or equal to x.
Solution.
The given function is g(x) = x – [x].
It is evident that g is defined at all integral points.
Let n be an integer.
Then, g(n) = n – [n] = n – n = 0
The left hand limit of f at x = n is
\(\lim _{x \rightarrow n^{-}}\) g(c) = \(\lim _{x \rightarrow n^{-}}\) (x – [x])
= \(\lim _{x \rightarrow n^{-}}\) (x) – \(\lim _{x \rightarrow n^{-}}\) [x] = n – (n – 1) = 1
The right hand limit of f at x = n is
\(\lim _{x \rightarrow n^{+}}\) g(x) = \(\lim _{x \rightarrow n^{+}}\) (x – [x])
= \(\lim _{x \rightarrow n^{+}}\) (x) – \(\lim _{x \rightarrow n^{+}}\) [x] = n – n = 0
It is observed that the left and right hand limits of f at x = n do not coincide.
Therefore, f is not continuous at x = n.
Hence, g is discontinuous at all integral points.

Question 20.
Is the function defined by f(x) = x2 – sin x + 5 continuous at x = π?
Solution.
The given function is f(x)= x2 – sin x + 5.
It is evident that f is defined at x = π.
At x = π, f(x) = f(π) = π2 – sin π + 5
= π2 – 0 + 5
= π2 + 5
Consider \(\lim _{x \rightarrow \pi}\) f(x) = \(\lim _{x \rightarrow \pi}\) (x2 – sin x + 5)
Put x = π + h
If x → π, then it is evident that h → 0
∴ \(\lim _{x \rightarrow \pi}\) f(x) = \(\lim _{x \rightarrow \pi}\) (x2 – sin x + 5)
= \(\lim _{h \rightarrow 0}\) [(π + h)2 – sin (π + h) + 5]
= \(\lim _{h \rightarrow 0}\) (π+ h)2 – \(\lim _{h \rightarrow 0}\) sin (π + h) + \(\lim _{h \rightarrow 0}\) 5
= (π + 0)2 – \(\lim _{h \rightarrow 0}\) [sin π cos h + cos π sin h] + 5
= π2 – \(\lim _{h \rightarrow 0}\) sin π cos h – \(\lim _{h \rightarrow 0}\) cos π sin h + 5
= π2 – sin π cos 0 – cos π sin 0 + 5
= π2 – 0 × 1 – (- 1) × 0 + 5
= π2 + 5
= \(\lim _{x \rightarrow \pi}\) f(x) = f(π)
Therefore, the given function f is continuous at x = π.

Question 21.
Discuss the continuity of the following functions.
(a) f(x) = sin x + cos x
(b) f(x) = sin x – cos x
(c) f(x) = sin x . cos x
Solution.
We know that if g and h are two continuous functions, then g + h, g-h, and g . h are also continuous.
It has to proved first that g(x) = sin x and h(x) = cos x are continuous functions.
Let g(x) = sin x
It is evident that g(x) = sin x is defined for every real number.
Let c be a real number.
Put x = c + h
If x → c, then h → 0
g(c) = sin c
⇒ \(\lim _{x \rightarrow c}\) g(x) = \(\lim _{x \rightarrow c}\) sinx
= \(\lim _{h \rightarrow 0}\) sin(c + h)
= \(\lim _{h \rightarrow 0}\) [sin c cos h + cos c sin h]
= \(\lim _{h \rightarrow 0}\) (sin c cos h) + \(\lim _{h \rightarrow 0}\) (cos c sin h)
= sin c cos 0 + cos c sin 0
= sin c + 0
= sin c
∴ \(\lim _{x \rightarrow c}\) g(x) = g(c)
Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number.
Put x = c + h
If x → c, then h → 0
h (c) = cos c
\(\lim _{x \rightarrow c}\) h(x) = \(\lim _{x \rightarrow c}\) cos x
= \(\lim _{h \rightarrow 0}\) cos (c + h) – \(\lim _{h \rightarrow 0}\) [cos c cos h – sin c sin h]
= \(\lim _{h \rightarrow 0}\) cos c cos h – \(\lim _{h \rightarrow 0}\) sin c sin h
= cos c cos 0 – sin c sin 0
= cos c × 1 – sin c × 0 = cos c
∴ = \(\lim _{x \rightarrow c}\) h(x) = h(c)
Therefore, h is a continuous function.
Therefore, it can be concluded that
(a) f(x) = g(x) + h(x) = sin x + cos x is a continuous function.
(b) f(x) = g(x) – h(x) = sin x – cos x is a continuous function.
(c) f(x) = g(x) x h(x) = sin x × cos x is a continuous function.

Question 22.
Discuss the continuity of the cosine, cosecant, secant and cotangent functions.
Solution.
It is known that if g and h are two continuous functions, then
(i) \(\frac{h(x)}{g(x)}\), g(x) ≠ 0 is continuous.
(ii) \(\frac{1}{g(x)}\), g(x) ≠ 0 is continuous.
(iii) \(\frac{1}{h(x)}\), h(x) ≠ 0 is continuous.
It has to be proved first that g(x) = sin x and h(x) = cos x are continuous functions.
Let g(x) = sin x
It is evident that g(x) = sin x is defined for every real number.
Let c be a real number.
Put x = c + h
If x → c, then h → 0
g(c) = sin c
\(\lim _{x \rightarrow c}\) g(x) = \(\lim _{x \rightarrow c}\) sin x
= \(\lim _{h \rightarrow 0}\) sin (c + h)
= \(\lim _{h \rightarrow 0}\) [sin c cos h + cos c sin h]
= \(\lim _{h \rightarrow 0}\) (sin c cos h) + \(\lim _{h \rightarrow 0}\) (cos c sin h)
= sin c cos 0 + cos c sin 0
= sin c + 0 = sin c
= \(\lim _{x \rightarrow c}\) g(x) = g(c)
Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number.
Put x = c + h
If x → c, then h → 0
h (c) = cos c
\(\lim _{x \rightarrow c}\) h(x) = \(\lim _{x \rightarrow c}\) cos x
= \(\lim _{h \rightarrow 0}\) cos(c + h)
= \(\lim _{h \rightarrow 0}\) [cos c cosh – sin c sin h]
= \(\lim _{h \rightarrow 0}\) cos c cos h – \(\lim _{h \rightarrow 0}\) sin c sin h
= cos c cos 0 – sin c sin 0
= cos c × 1 – sin c × 0 = cos c
∴ \(\lim _{x \rightarrow c}\) h(x) = h(c)
Therefore, h (x) = cos x is a continuous function.
It can be concluded that,
cosec x = \(\frac{1}{\sin x}\), sin x ≠ 0 is continuous.
⇒ cosec x, x ≠ nπ (n ∈ Z) is continuous.
Therefore, cosecant is continuous except at x = nπ, n ∈ Z
sec x = \(\frac{1}{\cos x}\), cos x ≠ 0 is continuous.
⇒ sec x, x ≠ (2n + 1) \(\frac{\pi}{2}\) (n ∈ Z) is continuous.
Therefore, secant is continuous except at x = (2n + 1) \(\frac{\pi}{2}\) (n ∈ Z)
cot x = \(\frac{\cos x}{\sin x}\), sin x ≠ 0 is continuous.
⇒ cot x, x ⇒ nπ (n ∈ Z) is continuous.
Therefore, cotangent is continuous except at x = nπ, n ∈ Z.

Question 23.
Find the points of discontinuity of f, where
f(x) = 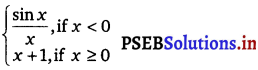
Solution.
The given function is f(x) = 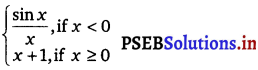
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
If c < 0, then f(c) = \(\frac{\sin c}{c}\) and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\left(\frac{\sin x}{x}\right)=\frac{\sin c}{c}\)
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x < 0. Case II: If c > 0, then /(c) = c + 1 and \(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (x + 1) = c + 1.
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x > 0.
Case III:
If c = 0, then f(c) = f(0) = 0 + 1 = 1
The left hand limit of f at x = 0 is
\(\lim _{x \rightarrow 0^{-}}\) f(x) = \(\lim _{x \rightarrow 0^{-}}\) = 1
The right hand limit of f at x = 0 is ,
\(\lim _{x \rightarrow 0^{+}}\) f(x) = \(\lim _{x \rightarrow 0^{+}}\) (x + 1) = 1
∴ \(\lim _{x \rightarrow 0^{-}}\) f(x) = \(\lim _{x \rightarrow 0^{+}}\) f(x) = f(0)
Therefore, f is continuous at x = 0.
From the above observations, it can be concluded that f is continuous at all points of the real line.
Thus, f has no point of discontinuity.

Question 24.
Determine if f defined by f(x) = 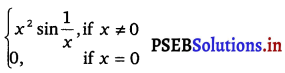
is a continuous function?
Solution.
The given function is f(x) = 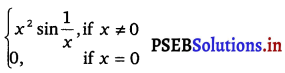
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
If c ≠ 0, then f(c) = c2 sin \(\frac{1}{c}\)
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\left(x^{2} \sin \frac{1}{x}\right)=\left(\lim _{x \rightarrow c} x^{2}\right)\left(\lim _{x \rightarrow c} \sin \frac{1}{x}\right)=c^{2} \sin \frac{1}{c}\)
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x ≠ 0.
Case II:
If c = 0, then f(0) = 0

Therefore, f is continuous at x = 0.
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.

Question 25.
Examine the continuity of f, where f is defined by f(x) = 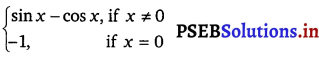
Solution.
The given function is f(x) = 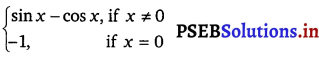
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
If c ≠ 0, then f(c) = sin c – cos c
\(\lim _{x \rightarrow c}\) f(x) = \(\lim _{x \rightarrow c}\) (sin x – cos x) = sin c – cos c
∴ \(\lim _{x \rightarrow c}\) f(x) = f(c)
Therefore, f is continuous at all points x, such that x ≠ 0.
Case II:
If c = 0, then f(0) = – 1
\(\lim _{x \rightarrow 0^{-}}\) f(x) = \(\lim _{x \rightarrow 0}\)] (sin x -cosx)
= sin 0 – cos 0 = 0 – 1 = – 1
\(\lim _{x \rightarrow 0^{+}}\) f(x) = \(\lim _{x \rightarrow 0}\) (sin x – cos x)
= sin 0 – cos 0 = 0 – 1 = – 1
∴ \(\lim _{x \rightarrow 0^{-}}\) f(x) = \(\lim _{x \rightarrow 0^{-}}\) f(x) = f(0)
Therefore, f is continuous at x = 0.
From the above observations it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.

Direction (26 – 29):
Find the values of k so that the function f is continuous at the indicated point.
Question 26.
f(x) = 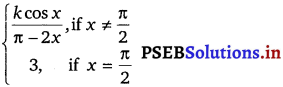 at x = \(\frac{\pi}{2}\).
at x = \(\frac{\pi}{2}\).
Solution.
The given function is f(x) = 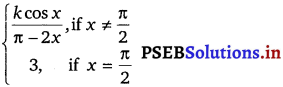
The given function f is continuous at x = \(\frac{\pi}{2}\) if f is defined at x = \(\frac{\pi}{2}\) and if the value of the f at x = \(\frac{\pi}{2}\) equals the limit of f at x = \(\frac{\pi}{2}\)
It is evident that f is defined at x = \(\frac{\pi}{2}\) and f(\(\frac{\pi}{2}\)) = 3.


Question 27.
f(x) = 
Solution.
The given function f is continuous at x = 2, if f is defined at x = 2 and if the value o f f at x = 2 equals the limit of f at x = 2.
It is evident that f is defined at x = 2 and f(2) = k(2)2 = 4k
∴ \(\lim _{x \rightarrow 2^{-}}\) f(x) = \(\lim _{x \rightarrow 2^{+}}\) f(x) = f(2)
⇒ \(\lim _{x \rightarrow 2^{-}}\) (kx2) = \(\lim _{x \rightarrow 2^{+}}\) (3) = 4k
⇒ k × 22 = 3 = 4k
⇒ 4k = 3 = 4k
⇒ 4k = 3
⇒ k = \(\frac{3}{4}\)
Therefore, the required value of k is \(\frac{3}{4}\).

Question 28.
f(x) = 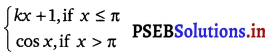 at x = π.
at x = π.
Solution.
The given function is f(x) = 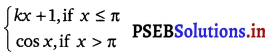
The given function f is continuous at x = π, if f is defined at x = n and if the value of π at x = π equals the limit of f at x = π.
It is evident that f is defined at x = π and f(π) = kπ + 1.
∴ \(\lim _{x \rightarrow \pi^{-}}\) f(x) = \(\lim _{x \rightarrow \pi^{+}}\) f(x) = f(π)
⇒ \(\lim _{x \rightarrow \pi^{-}}\) (kx + 1) = \(\lim _{x \rightarrow \pi^{+}}\) cos x = kπ + 1
⇒ kπ + 1 = cos π = kπ + 1
⇒ kπ + 1 = – 1 = kπ + 1
⇒ k = – \(\frac{2}{\pi}\)
Therefore, the required value of k is \(\frac{2}{\pi}\).
Question 29.
f(x) =  at x = 5
at x = 5
Solution.
The given function is f(x) = 
The given function f is continuous at x = 5, if f is defined at x = 5 and if the value of f at x = 5 equals the limit of f at x = 5.
It is evident that f is defined at x = 5 and f(5) = kx + 1 = 5k + 1.
∴ \(\lim _{x \rightarrow 5^{-}}\) f(x) = \(\lim _{x \rightarrow 5^{+}}\) f(5) = f(5)
⇒ \(\lim _{x \rightarrow 5^{-}}\) (kx + 1) = \(\lim _{x \rightarrow 5^{+}}\) (3x – 1) = 5k + 1
⇒ 5k + 1 = 15 – 5 = 5k + 1
⇒ 5k + 1 = 10
⇒ 5k = 9
⇒ k = \(\frac{9}{5}\)
Therefore, the required value of k is \(\frac{9}{5}\).

Question 30.
f(x) = 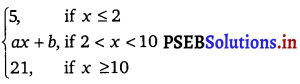
is a continuous function.
Solution.
The given function is f(x) = 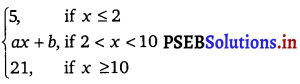
It is evident that the given function f is defined at all points of the real line.
If f is a continuous function, then f is continuous at all real numbers.
In particular, f is continuous at x = 2 and x = 10.
Since, f is continuous at x = 2, then we get
\(\lim _{x \rightarrow 2^{-}}\) f(x) = \(\lim _{x \rightarrow 2^{+}}\) f(x) = f(2)
⇒ \(\lim _{x \rightarrow 2^{-}}\) (5) = \(\lim _{x \rightarrow 2^{+}}\) (ax + b)= 5
⇒ 5 – 2a + b = 5
⇒ 2a + b = 5 ………….(i)
Since, f is continuous at x = 10, then we get
\(\lim _{x \rightarrow 10^{-}}\) f(x) = \(\lim _{x \rightarrow 10^{+}}\) f(x) = f(10)
⇒ \(\lim _{x \rightarrow 10^{-}}\) (ax + b) = \(\lim _{x \rightarrow 10^{+}}\)(21) = 21
⇒ 10a + b = 21 = 21
⇒ 10a + b = 21 …………(ii)
On subtracting Eq. (i) from Eq. (ii),
we get 8a = 16
⇒ a = 2
Putting a = 2 in Eq. (i), we get
2 × 2 + b = 5
⇒ 4 + b = 5
⇒ 6 = 1
Therefore, the values of a and b for which f is a continuous function, are 2 and 1, respectively.

Question 31.
Show that the function defined by f(x) = cos(x2) is a continuous function.
Solution.
Now f(x) = cos x2, let g(x) = cos x and h(x) = x2
∴ (goh) (x) = g(h(x)) = cos x2
Now g and h both are continuous for all x ∈ R
f(x) = (goh) (x) = cos x2 is also continuous at all x ∈ R.
Question 32.
Show that the function defined by f(x) = |cos x| is a continuous function.
Solution.
Let g(x) = |x| and h(x) = cos x
f(x) = (goh) (x) = g(h(x)) = g(cos x) = |cos x|
Now g(x) = |x| and h(x) = cos x both are continuous for all values of x ∈ R
∴ (goh) (x) is also continuous.
Hence f(x) = (goh) (x)
= |cos x| is continuous for all values of x ∈ R.

Question 33.
Examine that sin |x| is a continuous function.
Solution.
Let g(x) = sinx, h(x) = |x|
(goh) (x) = g(h(x)) = g(|x|) = sin |x| = f(x)
Now g(x) = sin x and h(x) = |x| both are continuous for all x ∈ R.
∴ f(x) = (goh)(x) = sin |x| is continuous at all x ∈ R.
Question 34.
Find all the points of discontinuity of f defined by f(x) =|x| – |x + 1|
Solution.
f(x) = |x| – |x + 1|
when x < – 1
f(x) = – x – [- (x + 1)]
= – x + x + 1 = 1
when – 1 ≤ x < 0
f(x) = – x – (x + 1) = – 2x – 1
when x ≥ 0
f(x) = x – (x + 1) = – 1
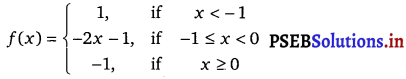
At x = – 1,
LHL = \(\lim _{x \rightarrow 1^{-}}\) f(x) = \(\lim _{x \rightarrow 1^{-}}\) (1) = 1
RHL = \(\lim _{x \rightarrow 1^{+}}\) f (x) = \(\lim _{x \rightarrow 1^{+}}\) (- 2x – 1) = 1
f(- 1) = – 2 (- 1) – 1 = 2 – 1 = 1
∴ LHL = RHL = f(- 1)
⇒ f is continuous at x = – 1.

At x = 0,
LHL = \(\lim _{x \rightarrow 0^{-}}\) (- 2x – 1) = – 1
f(0) = – 1 [Given]
RHL = \(\lim _{x \rightarrow 0^{+}}\) f(x) = \(\lim _{x \rightarrow 0^{+}}\) (- 1) = – 1
LHL = RHL = f(0)
f is continuous at x = 0
⇒ There is no point of discountinuous.
Hence, f is continuous for all x ∈ R.
![]()
![]()
![]()
![]()

![]()
![]()

![]()







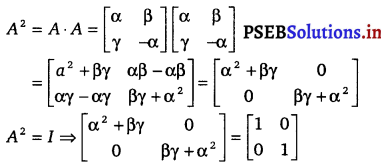














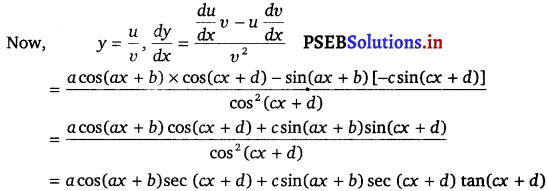

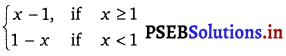

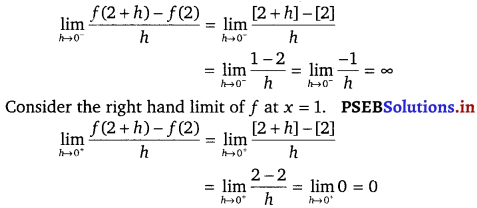














 continuous at x = 0? At x = 1? At x = 2?
continuous at x = 0? At x = 1? At x = 2?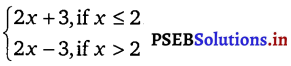
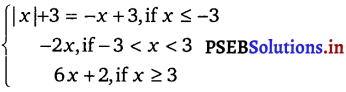

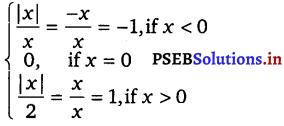
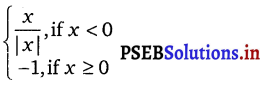
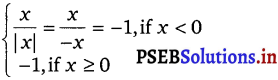
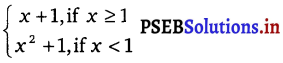
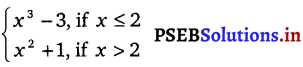
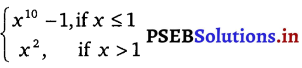



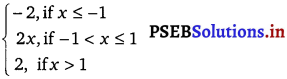

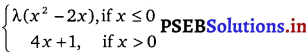
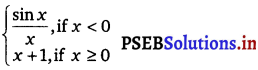
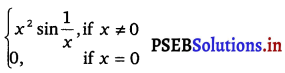

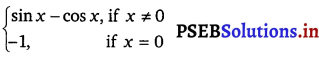
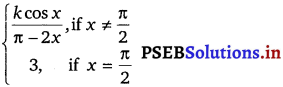 at x = \(\frac{\pi}{2}\).
at x = \(\frac{\pi}{2}\).

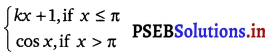 at x = π.
at x = π. at x = 5
at x = 5