Punjab State Board PSEB 12th Class Chemistry Book Solutions Chapter 7 The p-Block Elements Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Chemistry Chapter 7 The p-Block Elements
PSEB 12th Class Chemistry Guide The p-Block Elements InText Questions and Answers
Question 1.
Discuss the general characteristics of group 15 elements with reference to their electronic configuration, oxidation state, atomic size, ionisation enthalpy and electronegativity.
Answer:
General trends in group 15 elements
(i) Electronic configuration : All the elements of group 15 have ns2 np3 (5 valence electrons) electronic configuration in their valence shells.
The s-subshell is completely filled and p-subshell is exactly half-filled. This imparts extra stability to their electronic configuration.
Nitrogen (N7) = [He] 2s2 2p3
Phosphorus (P15) = [Ne] 3s2 3p3
Arsenic (As33 ) = [Ar] 3d10 4s2 4p3
Antimony (Sb51) = [Kr] 4d10 5s2 5p3
Bismuth (Bi83) = [Xe] 4f145d10 6s2 6p3
(ii) Oxidation state : All these elements have 5 valence electrons and require three more electrons to complete their octets. However, gaining electrons is very difficult as the nucleus will have to attract three more electrons. This can take place only with nitrogen as it is the smallest in size and the distance between the nucleus and the valence shell is relatively small. The remaining elements of this group show a formal oxidation state of – 3 in their covalent compounds. In addition to the – 3 state, N and P also show – 1 and – 2 oxidation states.
All the elements present in this group show + 3 and + 5 oxidation states. However, the stability of + 5 oxidation state decreases down a group, whereas the stability of +3 oxidation state increases. This happens because of the inert pair effect.
(iii) Atomic size : On moving down a group, the atomic size increases. This increase, in the atomic size is attributed to an increase in the number of shells.
(iv) Ionisation enthalpy First ionisation enthalpy decreases on moving down a group. This is because of increasing atomic sizes. Ionisation enthalpy of group 15 elements is greater than that of group 14 elements and group 16 elements in the corresponding periods. The order of successive ionisation enthalpies as expected is . △iH1 < △iH2 < △iH3.
Electronegativity : The electronegativity value decreases down the group with increasing atomic size.
Question 2.
Why does the reactivity of nitrogen differ from phosphorus?
Answer:
Nitrogen is chemically less reactive. This is because of the high stability of its molecule, N2. In N2, the two nitrogen atoms form a triple bond. This triple bond has very high bond strength, which is very difficult to break. It is because of nitrogen’s small size that it is able to form pn-pn bonds with itself. This property is not exhibited by atoms such as phosphorus. Thus, phosphorus is more reactive than nitrogen.
Question 3.
Discuss the trends in chemical reactivity of group 15 elements.
Answer:
General trends in chemical reactivity of group 15 elements are as follows :
(i) Reactivity towards hydrogen : The elements of group 15 react with hydrogen to form hydrides of type EH3, where E = N, P, As, Sb, or Bi. The stability of hydrides decreases on moving down from NH3 to BiH3.
(ii) Reactivity towards oxygen : The elements of group 15 form two types of oxides: E2O3 and E2O5 where E = N, P, As, Sb, or Bi. The oxide with the element in the higher oxidation state is more acidic than the other. However, the acidic character decreases on moving down a group.
(iii) Reactivity towards halogens : The group 15 elements react with halogens to form two series of salts: EX3 and EX5. However, nitrogen does not form NX5 as it lacks the d-orbital. All trihalides (except NX3) are stable.
(iv) Reactivity towards metals : The group 15 elements react with metals to form binary compounds in which metals exhibit – 3 oxidation states.
![]()
Question 4.
Why does NH3form hydrogen bond but PH3 does not?
Answer:
Nitrogen is highly electronegative as compared to phosphorus. This causes a greater attraction of electrons towards nitrogen in NH3 than towards phosphourus in PH3. Hence, the extent of hydrogen bonding in PH3 is very less as compared to NH3.
Question 5.
How is nitrogen prepared in the laboratory? Write the chemical equations of the reactions involved.
Answer:
(i) In the laboratory, nitrogen is prepared by treating an aqueous solution of ammonium chloride with sodium nitrite.
NH4Cl(aq) + NaNO2(aq) → N2(g) + 2H2O(Z) + NaCl(aq)
NO and HNO3 are produced in small amounts. These are impurities that can be removed on passing nitrogen gas through aqueous sulphuric acid, containing potassium dichromate.
(ii) Pure nitrogen is also obtained by thermal decomposition of sodium or barium azide.

Question 6.
How is ammonia manufactured industrially?
Answer:
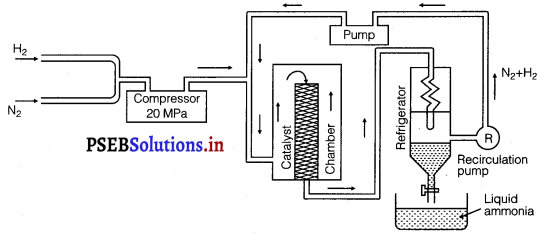
Ammonia is prepared on a large-scale by the Haber’s process.
According to Le-Chatelier’s principle high pressure would favour the production of ammonia. Optimum conditions for production of NH3 are
(i) Temperature—700 K
(ii) Pressure—200 × 105 Pa
(iii) Catalyst—Fe2O3
(iv) Promotor—K2O and Al2O3
![]()
Question 7.
Illustrate how copper metal can give different products on reaction with HNOs.
Answer:
Concentrated nitric acid is a strong oxidising agent. It is used for oxidising most metals. The products of oxidation depend on the concentration of the acid, temperature and also on the material undergoing oxidation.
3Cu + 8HNO3(dilute) → 3CU(NO3)2 + 2NO + 4H2O
Cu + 4HNO3(conc.) → CU(NO3)2 + 2NO2 + 2H2O
Question 8.
Give the resonating structures of N02 and N205.
Answer:
1. Resonating structures of NO2
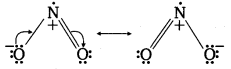
2. Resonating structures of NO2O5
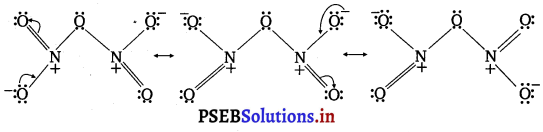
Question 9.
The HNH angle value is higher than HPH, HAsH and HSbH angles. Why?
[Hint : Can be explained on the basis of sp3 hybridisation in NH3 and only s-p bonding between hydrogen and other elements of the group.]
Answer:
It can be explained on the basis of sp3 hybridisaton in NH3 and only s-p bonding between hydrogen and other elements of the group.
![]()
As we move down the group, the size of the central atom goes on increasing and its electronegativity goes on decreasing. As a result, the bond pairs of electrons tend to lie away from the central atom as we move from NH3 to SbH3. In other words, the force of repulsion between the adjacent bond pairs is maximum in NH3 minimum in SbH3. Consequently the bond angle is maximum in NH3 and minimum in SbH3.
![]()
Question 10.
Why does R3P = 0 exist but R3N = 0 does not (R = alkyl group)?
Answer:
N due to the absence of d-orbitals, cannot form pn-dn multiple bonds. Thus, N cannot expand its covalency beyond four but in R3N = O, N has a covalency of 5. So, the compound R3N — O does not exist. On the other hand, P due to the presence of d-orbitals forms pπ-dπ multiple bonds and hence can expand its covalency beyond 4. Therefore, P forms R3P = O in which the covalency of P is 5.
Question 11.
Explain why NH3 is basic while BiH3 is only feebly basic.
Answer:
Since, the atomic size of N (70 pm) is much smaller than that of Bi (148 pm), electron density on the N-atom is much higher than that on Bi-atom. As a result, the tendency of N in NH3 to donate its lone pair of electrons is much higher than that of Bi in BiH3. Thus, NH3 is much more basic than BiH3.
Question 12.
Nitrogen exists as diatomic molecule and phosphorus as P4. Why?
Answer:
Nitrogen owing to its small size has a tendency to form pπ-pπ multiple bonds with itself. Nitrogen thus forms a very stable diatomic molecule, N2. On moving down a group, the tendency to form pπ-pπ bonds decreases (because of the large size of heavier elements). Therefore, phosphorus (like other heavier metals) exists in the P4 state.
![]()
Question 13.
Write main differences between the properties of white phosphorus and red phosphorus.
Answer:
| White, Phosphorus | Red Phosphorus |
| 1. It is a soft and waxy solid. It possesses a garlic smell. | It is a hard and crystalline solid, without any smell. |
| 2. It is poisonous. | It is non-poisonous. |
| 3. It is insoluble in water but soluble in carbon disulphide. | It is insoluble in both water and carbon disulphide. |
| 4. It undergoes spontaneous combustion in air. | It is relatively less reactive. |
| 5. P4 molecules are held by weak van der Waal’s forces. | P4 molecules are held by covalent bonds in polymeric structure. |
| 6. Bums easily in Cl2 forming PCl3 and PCl5. | Combines with Cl2 only on heating. |
Question 14.
Why does nitrogen show catenation properties less than phosphorus?
Answer:
Catenation is much more common in phosphorus compounds than in nitrogen compounds. This is because of the relative weakness of the N—N single bond as compared to the P—P single bond. Since nitrogen atom is smaller, there is greater repulsion of electron density of two nitrogen atoms, thereby weakening die N—N single bond.
Question 15.
Give the disproportionation reaction of H3PO3.
Answer:
On heating, orthophosphorus acid (H3PO3) disproportionates to give orthophosphoric acid (H3PO4) and phosphine (PH3). The oxidation states of P in various species involved in the reaction are mentioned below :
![]()
Thus, H3PO3 (oxidation state +3) oxidises to give H3PO4 (oxidation state + 5) and reduce to produce phosphine (oxidation state – 3)
![]()
Question 16.
Can PCl5 act as an oxidising as well as a reducing agent? Justify.
Answer:
PCl5 can only act as an oxidising agent. The highest oxidation state that P can show is + 5. In PCl5, phosphorus is in its highest oxidation state (+5). However, it can decrease its oxidation state and act as an oxidising agent. e.g.,
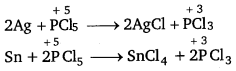
Question 17.
Justify the placement of O, S, Se, Te and Po in the same group of the periodic table in terms of electronic configuration, oxidation state and hydride formation.
Answer:
(i) Electronic configuration : The electronic configuration of the elements of group 16 is given below: .
O8 = [He] 2s2 2p4
S16 = [Ne] 3s2 3p4
Se34 = [Ar]3d10 4s2 4p4
Te52 = [Kr] 4d10 5s2 5p4
PO84 = [Xe] 4f14 5d10 6s2 6p4
All these elements have similar valence shell configuration ns2 np4, hence their position in group 16 with each other is justified.
(ii) Oxidation state : As these elements have six valence electrons (ns2 np4), they should display an oxidation state of – 2. However, only oxygen predominantly shows the oxidation state of -2 owing to its high electronegativity. It also exhibits the oxidation state of -1 (H2O2), zero (O2), and + 2(OF2). However, the stability of the -2 oxidation state decreases on moving down a group due to a decrease in the electronegativity of the elements. The heavier elements of the group show an oxidation state of + 2, + 4, and + 6 due to the availability of d-orbitals.
(iii) Formation of hydrides : These elements form hydrides of formula H2E, where E = O, S, Se, Te, Po. Oxygen and sulphur also form hydrides of type H2E2. These hydrides are quite volatile in nature.
Question 18.
Why is dioxygen a gas but sulphur a solid?
Answer:
Oxygen is smaller in size as compared to sulphur. Due to its smaller size, it can effectively form pπ—pπ bonds and form O2(0=0) molecule. Also, the intermolecular forces in oxygen are weak van der Waal’s, which cause it to exist as gas. On the other hand, sulphur does not form M2 molecule but exists as a puckered structure held together by strong covalent bonds. Hence, it is a solid.
![]()
Question 19.
Knowing the electron gain enthalpy values for O → O– and O → O2- as- 141 and 702 kJ mol-1 respectively, how can you account for the formation of a large number of oxides having O 2- species and not O–?
[Hint : Consider lattice energy factor in the formation of compounds).
Answer:
Stability of an ionic compound depends on its lattice energy. More the lattice energy of a compound, more stable it will be.
Lattice energy is directly proportional to the charge carried by an ion. When a metal combines with oxygen, the lattice energy of the oxide involving O2-ion is much more than the oxide involving O– ion. Hence, the oxide having O2- ions are more stable than oxides having O–. Hence, we can say that formation of O2- is energetically more favourable than formation of O–.
Question 20.
Which aerosols deplete ozone?
Answer:
Freons or chlorofluorocarbons (CFCs) are aerosols that accelerate the depletion of ozone. In the presence of ultraviolet radiations, molecules of CFCs break down to form chlorine-free radicals that combine with ozone to form oxygen.
Question 21.
Describe the manufacture of H2SO4 by contact process?
Answer:
H2SO4 is prepared by contact process. The acid produced by this process is free from arsenic impurities and is of high purity. The process involves the following steps:
Step I: Preparation of sulphur dioxide : Preparation of SO2 by burning of sulphur or roasting pyrites.
S8(s) + 😯2(g) → 8SO2
Step II: Conversion of sulphur dioxide to sulphur trioxide : Sulphur dioxide convert into sulphur trioxide when SO2 react with oxygen in presence of V2O5 at 720 K temperature.
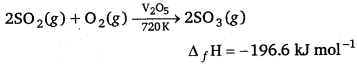
Step III: Formation of oleum : Sulphur trioxide so formed is absorbed in sulphuric acid to form oleum.
SO3 + H2SO4 → H2S2O7
Step IV : Oleum change into H2SO4 :
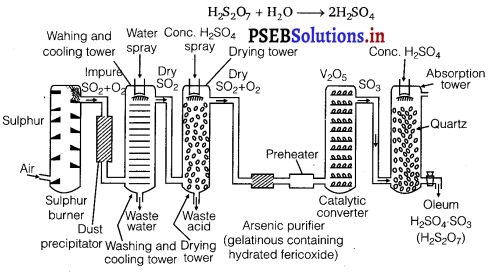
![]()
Question 22.
How is SO2 an air pollutant?
Answer:
Sulphur dioxide causes harm to the environment in many ways:
1. It combines with water vapour present in the atmosphere to form, sulphuric acid. This causes acid rain. Acid rain damages soil, plants, and buildings, especially those made of marble.
2. Even in very low concentrations, SO2 causes irritation in the respiratory tract. It causes throat and eye irritation and can also affect the larynx to cause breathlessness.
3. It is extremely harmful to plants. Plants exposed to sulphur dioxide for a long time lose colour from their leaves. This condition is known as chlorosis. This happens because the formation of chlorophyll is affected by the presence of sulphur dioxide.
Question 23.
Why are halogens strong oxidising agents?
Answer:
The general electronic configuration of halogens is np5, where n = 2 – 6. Thus, halogens need only one more electron to complete their octet and to attain the stable noble gas configuration. Also, halogens are highly electronegative with low dissociation energies and high negative electron gain enthalpies. Therefore, they have a high tendency to gain an electron. Hence, they act as strong oxidising agents.
Question 24.
Explain why fluorine forms only one oxoacid, HOF.
Answer:
Fluorine is known to form only one oxoacid, HOF which is highly unstable. Other halogens form oxoacids of the type HOX, HXO2, HXO3 and HXO4 (X = Cl, Br, I). Fluorine due to its small size, absence of d-orbital and high electronegativity cannot act as central atom in higher oxoacids and hence do not form higher oxoacids.
![]()
Question 25.
Explain why inspite of nearly the same electronegativity, nitrogen forms hydrogen bonding while chlorine does not.
Answer:
Electronegativity of both nitrogen (N) as well as chlorine (Cl) is 3.0. But only nitrogen forms hydrogen bonding not chlorine. The reason is that atomic size of N (atomic radius = 70 pm) is less as compared to chlorine (atomic radius =99 pm) therefore, N can cause greater polarisation of N—H bond than Cl in case of Cl—H bond. Hence, N atom is involved in hydrogen bonding and not chlorine.
Question 26.
Write two uses of ClO2.
Answer:
Uses of ClO2
- It is used for purifying water.
- It is used as a bleaching agent.
Question 27.
Why are halogens coloured?
Answer:
Almost all halogens are coloured. This is because halogens absorb radiations in the visible region. This results in the excitation of valence electrons to a higher energy region. Since, the amount of energy required for excitation differs for each halogen, each halogen displays a different colour.
Different colours of halogens are given below :
Fluorine — Yellow
Chlorine — Greenish yellow
Bromine — Red
Iodine — Violet
![]()
Question 28.
Write the reactions of F2 and Cl2 with water.
Answer:
(i) Fluorine reacts with water to produce oxygen and ozone.
2F2(g) + 2H2O(l) → O2(g) + 4HF(aq)
3F2(g) + 3H2O(l) → 6HF (aq) + O3(g)
(ii) Chlorine reacts with water in presence of sunlight to produce nascent oxygen.

Question 29.
How can you prepare Cl2 from HCl and HCl from Cl2? Write reactions only.
Answer:
HCl can be oxidised to Cl2 by a number of oxidising agents like MnO2, KMnO4.
MnO2 + 4HCl → MnCl2 + Cl2 + 2H2O
C2 can be reduced to HCl by reacting with H2 in the presence of diffused sunlight.
![]()
Question 30.
What inspired N. Bartlett for carrying out reaction between Xe and PtF6?
Answer:
Neil Bartlett observed that PtF6 reacts with O2 to yield an ionic solid, \(\mathrm{O}_{2}^{+} \mathrm{PtF}_{6}^{-}\).
O2(g) + PtF6(g) → \(\mathrm{O}_{2}^{+} \mathrm{PtF}_{6}^{-}\)
Here, O2 gets oxidised to \(\mathrm{O}_{2}^{+}\) by PtF6.
Since, the first ionisation enthalpy of Xe (1170 kJ mol-1) is fairly close to that of O2 molecules (1175 kJ mol-1), Bartlett thought that PtF6 should also oxidise Xe to Xe+. This inspired Bartlett to carry out the reaction between Xe and PtF2. When Xe and PtF6 were mixed, a rapid reaction occurred and a red solid with the formula, Xe+[PtF6]– was obtained.
![]()
Question 31.
What are the oxidation states of phosphorus in the following:
(a) H3PO3
(b) PCl3
(c) Ca3P2
(d) Na3PO4
(e) POF3.
Answer:
We know, the general valency of H = +1, O = – 2, Ca = + 2, Na = +1, F = -1, Cl = -1

Question 32.
Write balanced equations for the following:
(i) NaCl is heated with sulphuric acid in the presence of MnO2.
(ii) Chlorine gas is passed into a solution of Nal in water.
Answer:
(i) 4NaCl + MnO2 + 4H2SO4 → MnCl2 + 4NaHSO4 + 2H2O + Cl2
(ii) Cl2 + Nal → 2NaCl + I2
Question 33.
How are xenon fluorides XeF2, XeF4 and XeF6 obtained?
Answer:
Preparation of XeF2, XeF4 and XeF6 :
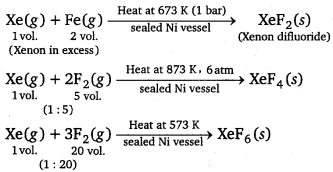
![]()
Question 34.
With what neutral molecule is CIO– isoelectronic? Is that molecule a Lewis base?
Answer:
CIO– has 26 electrons [ 17 (Cl) + 8 (0) + le– (charge)]. The neutral molecule which is isoelectronic with it is C1F (17 + 9) = 26e–. ClF is a Lewis base.
Question 35.
How are XeO3 and XeOF4 prepared?
Answer:
Hydrolysis of XeF4 and XeF6 with water gives XeO3.
6XeF4 + 12H2O → 4Xe + 2XeO3 + 24HF + 3O2
XeF6 + 3H2O → XeO3 + 6HF
In contrast, partial hydrolysis of XeF6 gives XeOF4.
XeF6 + H2O → XeOF4 + 2HF
Question 36.
Arrange the following in the order of property indicated for each set:
(i) F2, Cl2, Br2, I2—increasing bond dissociation enthalpy.
(ii) HF, HCl, HBr, HI—increasing acid strength.
(iii) NH3, PH3, ASH3, SbH3, BiH3—increasing base strength.
Answer:
(i) In the order of increasing bond dissociation enthalpy : Bond dissociation enthalpy decreases as the bond distance increases, so dissociation enthalpy increases as below :
I—I < F—F < Br—Br < Cl—Cl
(ii) In the order of increasing acid strength in water (i.e., aqueous solution) :
As the size of atom increases, then bond dissociation enthalpy of H—X bond decreases. So, acidic strength increases as below :
HF < HCl < HBr < HI
(iii) In the order of increasing base strength :
As we move from NH3 to BiH3, the size of the atom increases. Consequently, the electron density on the central atom decreases, so basic strength increases as below :
![]()
![]()
Question 37.
Which one of the following does not exist?
(i) XeOF4
(ii) NeF2
(iii) XeF2
(iv) XeF6
Answer:
The sum of first and second ionisation enthalpies of Ne are much higher than those of Xe. Thus, F2 can oxidise Xe to Xe2+ but cannot oxidise Ne to Ne2+. In other words, NeF2 does not exist and all the xenon fluorides (XeF2 and XeF6) and xenon oxyfluoride (XeOF4) do exist.
Question 38.
Give the formula and describe the structure of a noble gas species which is isostructural with :
(i) \(\mathrm{ICl}_{4}^{-}\)
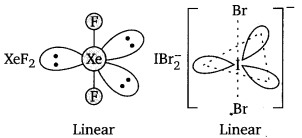
(ii) \(\mathrm{IBr}_{2}^{-}\)
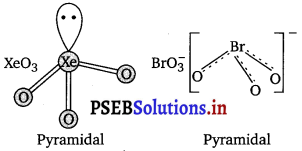
(iii) \(\mathrm{BrO}_{3}^{-}\)
Answer:
(i) In \(\mathrm{ICl}_{4}^{-}\), the central atom “I” has 7 valence electrons and one negative charge. Four of these form single bonds with four Cl atoms (four bond pairs) while the remaining four constitute two lone pairs, so according to VSEPR theory, it should be square planar. \(\mathrm{ICl}_{4}^{-}\) has 7 + 4×7 + 1= 36 valence electrons. A noble gas species having 36 valence electrons is XeF4 (8 + 4 × 7 = 36). Thus, \(\mathrm{ICl}_{4}^{-}\) and XeF4, both are square planar.
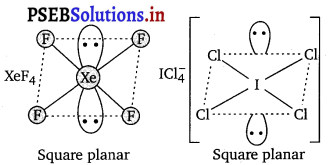
(ii) In \(\mathrm{IBr}_{2}^{-}\), the central atom “I” has 7 valence electrons and one negative charge. Two of these form two single bonds with two Br atoms, while the remaining six constitute three lone pair. Thus, I in \(\mathrm{IBr}_{2}^{-}\) has two bond pairs and three lone pairs, so according to VSEPR theory, it should be linear.
\(\mathrm{IBr}_{2}^{-}\) has 7 + 2×7 + 1=22 valence electrons. A noble gas species having 22 valence electrons is XeF2 (8 + 2 × 7 = 22). Thus, \(\mathrm{IBr}_{2}^{-}\) and XeF2 both are linear.
(iii) In \(\mathrm{BrO}_{3}^{-}\), the central atom “Br” has seven electrons and one negative charge. Four of these electrons form double bonds with oxygen atoms while fifty electrons forms a single bond with O– ion. The remaining two electrons form one lone pair, so according to VSEPR theory, it should be pyramidal.
\(\mathrm{BrO}_{3}^{-}\) has 7 + 3 × 6 + 1 = 26 valence electrons. A noble gas species having 26 valence electrons is XeO3 (8 + 3 × 6 = 26). Thus, \(\mathrm{BrO}_{3}^{-}\) and XeO3 both are pyramidal.
Question 39.
Why do noble gases have comparatively large atomic sizes?
Answer:
The atomic size, in the case of noble gases, is expressed in terms of van der radii whereas the atomic size of other members of the period is either metallic radii or covalent radii. As the van der radii is larger than both metallic as well as covalent radii, therefore the atomic size of noble gas is quite large. Among the noble gases, the atomic size increases down the group due to addition of new electronic shells.
![]()
Question 40.
List the uses of neon and argon gases.
Answer:
(i) Uses of Neon
- It is used in neon discharge lamps and signs which are used for advertising purposes.
- It is used in safety devices for protecting electrical instruments because it has a property of carrying exceedingly high currents under high voltage.
(ii) Uses of Argon
- It is widely used in filling incandescent metal filament electric bulbs.
- It is used for filling radio-valves, rectifiers and fluorescent tubes.
Chemistry Guide for Class 12 PSEB The p-Block Elements Textbook Questions and Answers
Question 1.
Why are pentahalides more covalent than trihalides?
Answer:
In pentahalides, the oxidation state is +5 and in trihalides, the oxidation state is +3. Since the metal ion with a high charge has more polarising power, pentahalides are more covalent than trihalides.
Question 2.
Why is BiH3 the strongest reducing agent amongst all the hydrides of group 15 elements?
Answer:
As we move down a group, the atomic size increases and the stability of the hydrides of group 15 elements decreases. Since, the stability of hydrides decreases on moving from NH3 to BiH3, the reducing character of the hydrides increases on moving from NH3 to BiH3.
![]()
Question 3.
Why is N2 less reactive at room temperature?
Answer:
The two N atoms in N2 are bonded to each other by very strong triple covalent bonds. The bond dissociation energy of this bond is very high. As a result, N2 is less reactive at room temperature.
Question 4.
Mention the conditions required to maximise the yield of ammonia.
Answer:
Ammonia is produced by Haber’s process as
![]()
Yield of ammonia is favoured by high pressure according to Le-Chatelier’s principle. Other conditions, that favour the production of ammonia are as follows:
- High pressure (200 atm or 200 × 105 Pa)
- Temperature approximately 700 K
- Use of a catalyst such as iron oxide mixed with small amounts of Mo or K2O and Al2O3.
Question 5.
How does ammonia react with a solution of Cu2+ ?
Answer:
Ammonia reacts with a solution of Cu2+ by donating a lone pair of electrons.
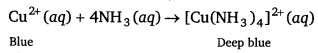
![]()
Question 6.
What is the covalence of nitrogen in N2O5?
Answer:
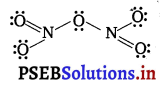
From the structure of N2O5, it is evident that the covalence of nitrogen is 4.
Question 7.
Bond angle in \(\mathbf{P H}_{4}^{+}\) is higher than that in PH3. Why?
Answer:
In PH3, P is sp3 hybridised. Three orbitals are involved in bonding with three hydrogen atoms and the fourth one contains a lone pair. As lone pair-bond pair repulsion is stronger than bond pair-bond pair repulsion, the tetrahedral shape associated with sp3 bonding is changed to pyramidal. PH3 combines with a proton to form \(\mathbf{P H}_{4}^{+}\) in which the lone pair is absent. Due to the absence of lone pair in \(\mathbf{P H}_{4}^{+}\), there is no lone pair-bond pair repulsion. Hence, the bond angle in \(\mathbf{P H}_{4}^{+}\) is higher than the bond angle in PH3.
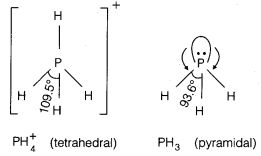
Question 8.
What happens when white phosphorus is heated with concentrated NaOH solution in an inert atmosphere of CO2?
Answer:
White phosphorus dissolves in boiling NaOH in an inert atmosphere of CO2 to give phosphine (PH3) and sodium hypophosphite (NaH2PO2).
![]()
![]()
Question 9.
What happens when PCl5 is heated?
Answer:
All the bonds that are present in PCl5 are not similar. It has three equatorial and two axial bonds. The equatorial bonds are stronger than the axial ones. Therefore, when PCl5 is heated strongly, it decomposes to form PCl3.
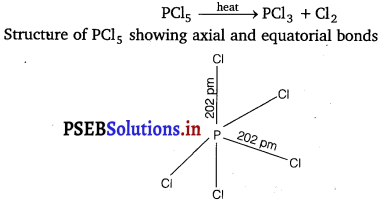
Question 10.
Write a balanced-equation for the hydrolytic reaction of PCl5 in heavy water.
Answer:
Hydrolytic reaction of PCl5 in heavy water (D2O)
PCl5 + D2O → POCl3 + 2DCl
POCl3 + 3D2O → D3PO4 + 3DCl
Therefore, the net reaction can be written as
PCl5 + 4D2O → D3PO4 + 5DCl
Question 11.
What is the basicity of H3PO4?
Answer:
The structure of H3PO4 is as
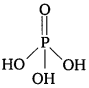
Since there are three OH groups present in H3PO4 its basicity is three i.e., it is a tribasic acid.
![]()
![]()
Question 12.
What happens when H3PO3 is heated?
Answer:
H3PO3, on heating, undergoes disproportionation reaction to form PH3 and H3PO4. The oxidation numbers of P in H3PO3,PH3, and H3PO4 are +3, -3, and + 5 respectively. As the oxidation number of the same element is decreasing and increasing during a particular reaction, the reaction is a disproportionation reaction.

Question 13.
List the important sources of sulphur.
Answer:
Sulphur mainly exists in combined form in the fearth’s crust primarily as sulphates [gypsum (CaSO4∙2H2O), Epsom salt (MgSO4∙7H2O), baryte (BaSO4)] and sulphides [galena (PbS), zinc blends (ZnS), copper pyrites (CuFeS2)].
Traces of sulphur occur as H2S in volcanoes. Organic materials such as eggs, garlic, onion, mustard, hair and wool also contain sulphur.
Question 14.
Write the order of thermal stability of the hydrides of group 16 elements.
Answer:
The thermal stability of hydrides decreases on moving down the group. This is due to a decrease in the bond dissociation enthalpy of hydrides on moving down the group.
Thus, the order of bond dissociation enthalpy is
H2O > H2S > H2Se > H2Te > H2PO
This is also the order of thermal stability.
![]()
Question 15.
Why is H2O a liquid and H2S a gas?
Answer:
H2O has oxygen as the central atom. Oxygen has smaller size and higher electronegativity as compared to sulphur. Therefore, there is extensive hydrogen bonding in H2O, which is absent in H2S. Molecules of H2S are held together only by weak van der Waal’s forces of attraction.
Hence, H2O exists as a liquid while H2S as a gas.
Question 16.
Which of the following does not react with oxygen directly?
Zn, Ti, Pt, Fe
Answer:
Pt is a noble metal and does not react very easily. All other elements, Zn, Ti, Fe, are quite reactive. Hence, oxygen does not react with platinum (Pt) directly.
Question 17.
Complete the following reactions:
(i) C2H4 + O2 →
(ii) 4Al + 3O2 →
Answer:
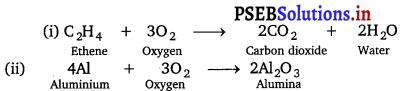
![]()
Question 18.
Why does O3 act as a powerful oxidising agent?
Answer:
Ozone is not a very stable compound under normal conditions and decomposes readily on heating to give a molecule of oxygen and nascent oxygen. Nascent oxygen, being a free redical, is very reactive.
![]()
Therefore, ozone acts as a powerful oxidising agent.
Question 19.
How is O3 estimated quantitatively?
Answer:
Quantitatively, ozone can be estimated with the help of potassium iodide. When ozone is made to react with potassium iodide solution buffered with a borate buffer (pH 9.2), iodine is liberated. This liberated iodine can be titrated against a standard solution of sodium thiosulphate using starch as an indicator. The reactions involved in the process are given below :
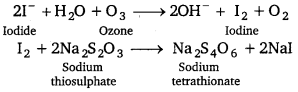
Question 20.
What happens when sulphur dioxide is passed through an aqueous solution of Fe(Ill) salt?
Answer:
When SO2 is passed through an aqueous solution of Fe(III) i.e., ferric salt, it is reduced to Fe(II) i.e. ferrous salt. Here, SO2 acts as a reducing agent.
2Fe3+ + SO2 + 2H2O → 2Fe2+ + \(\mathrm{SO}_{4}^{2-}\) + 4H+
![]()
Question 21.
Comment on the nature of two S-O bonds formed in SO2 molecule. Are the two S—O bonds in this molecule equal?
Answer:
Both the S—O bonds in SO2 are covalent and have equal strength due to resonating/canonical structure. These are equal with bond length = 143 pm. The resonating structures of SO2 are as follows :
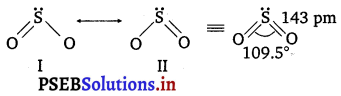
Question 22.
How is the presence of SO2 detected?
Answer:
SO2 is a colourless and pungent smelling gas. Two tests to detect the presence of SO2 are as follows:
(i) SO2 decolourises acidified KMnO4 solution.
![]()
(ii) SO2 changes the colour of acidified potassium dichromate solution from orange to green
![]()
Question 23.
Mention three areas in which H2SO4 plays an important role.
Answer:
Sulphuric acid is an important industrial chemical and is used for a lot of purposes. Some important uses of sulphuric acid are given below:
- It is used in fertiliser industry. It is used to make various fertilisers such as ammonium sulphate and calcium super phosphate.
- It is used in the manufacture of pigments, paints, and detergents.
- It is used in the manufacture of storage batteries.
![]()
Question 24.
Write the conditions to maximise the yield of H2SO4 by contact process.
Answer:
The key step in the manufacture of H2SO4 is catalytic oxidation of SO2 to produce SO3 in presence of V2O5.
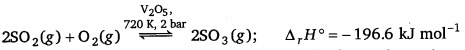
The reaction is exothermic, reversible and the forward reaction results in the decrease in volume. Thus, according to Le-Chatelier’s principle, the forward reaction should be favoured by low temperature and high pressure. But the temperature should not be very low otherwise the rate of reaction will become very slow.
Question 25.
Why is Ka2 << Ka1 for H2SO4 in water?
Answer:
H2SO4 is a strong dibasic acid. It ionises in two steps and has two dissociation constants.
H2SO4(aq) + H2O(l) → H3O+(aq) + \(\mathrm{HSO}_{4}^{-}\)(aq); Ka1 >10
\(\mathrm{HSO}_{4}^{-}\)(aq) + H2O(l) → H3O+(aq) + \(\mathrm{SO}_{4}^{-}\)(aq); Ka2 = 1.2 × 10-2
Ka1 >> K12
Because the negatively charged HSO4 ions have much less tendency to donate a proton to H2O as compared to neutral H2SO4.
Question 26.
Considering the parameters such as bond dissociation enthalpy, electron gain enthalpy and hydration enthalpy, compare the oxidising power of F2 and C2.
Answer:
The electrode potential depends upon the parameters indicated below :
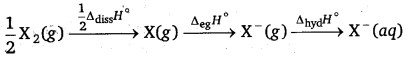
| (Values of kJ mole-1) | △dissH | △egH | △hydH |
| Fluorine | 158.8 | -333 | 515 |
| Chlorine | 242.6 | -349 | 381 |
The two factors, high hydration enthalpy of F-1 ion (515 kJ mol-1) and low F—F bond dissociation enthalpy more than compensate the less negative electron gain enthalpy of fluorine. Due to this, electrode potential of F2 (+2.87 V) is much higher than that of Cl2 (+1.36 V) and hence F2 is a stronger oxidising agent than Cl2.
![]()
Question 27.
Give two examples to show the anomalous behaviour of fluorine.
Answer:
Anomalous behaviour of fluorine
- It forms only one oxoacid as compared to other halogens that form a number of oxoacids.
- Ionisation enthalpy, electronegativity, and electrode potential of fluorine are much higher than expected.
Question 28.
Sea is the greatest source of some halogens. Comment.
Answer:
Sea water contains chlorides, bromides, and iodides of Na, K, Mg, and Ca. However, it primarily contains NaCl. The deposits of dried up sea beds contain sodium chloride and camallite, KCl ∙ MgCl2 ∙ 6H2O. Marine life also contains iodine in their systems. For example, sea weeds contain upto 0.5% iodine as sodium iodide. Thus, sea is the greatest source of some halogens.
Question 29.
Give the reason for bleaching action of Cl2.
Answer:
When chlorine reacts with water, it produces nascent oxygen. This nascent oxygen then combines with the coloured substances present in the organic matter to oxide them into colourless substances.
Cl2 + H2 → 2HCl + [O]
Coloured substance + [O] → Colourless substance
Bleaching action of chlorine creates permanent effect. It bleaches the vegetable or organic matter in the presence of moisture.
![]()
Question 30.
Name two poisonous gases which can be prepared from chlorine gas.
Answer:
Two poisonous gases that can be prepared from chlorine gas are
- Phosgene (COCl2)
- Mustard gas (ClCH2CH2SCH2CH2Cl)
Question 31.
Why is ICl more reactive than I2?
Answer:
ICl is more reactive than I2 because I—Cl bond in IC1 is weaker than I—I bond in I2 due to less bond dissociation energy consequently I-Cl break easily to form halogen atoms which readily bring about the reactions.
Question 32.
Why is helium used in diving apparatus?
Answer:
Air contains a large amount of nitrogen and the solubility of gases in liquids increases with increase in pressure. When sea divers dive deep into the sea, large amount of nitrogen dissolves in their blood. When they come back to the surface, solubility of nitrogen decreases and it separates from the blood and forms small air bubbles. This leads to a dangerous medical condition called bends. Therefore, air in oxygen cylinders used for diving is diluted with helium gas. This is done as He is sparingly less soluble in blood.
![]()
Question 33.
Balance the following equation: XeF6 + H2O → XeO2F2 + HF
Answer:
Balanced equation
XeF6 + 2H2O → XeO2F2 + 4HF
Question 34.
Why has it been difficult to study the chemistry of radon?
Answer:
It is difficult to study the chemistry of radon because it is a radioactive substance having a half-life of only 3.82 days. Also, compounds of radon such as RnF2 have not been isolated. They have only been identified.






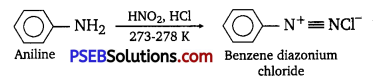

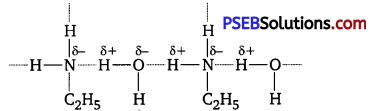

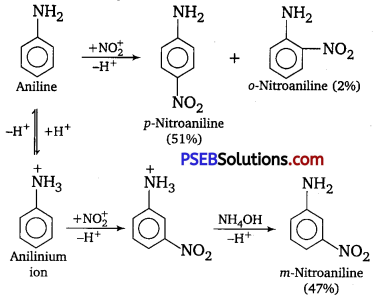

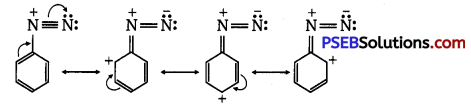
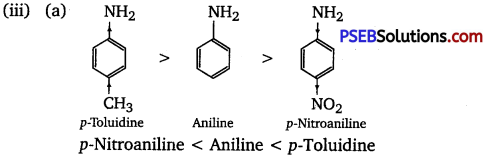
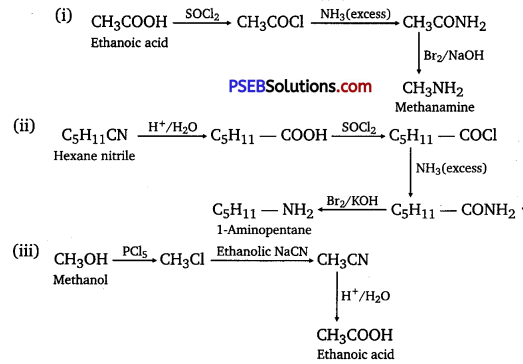
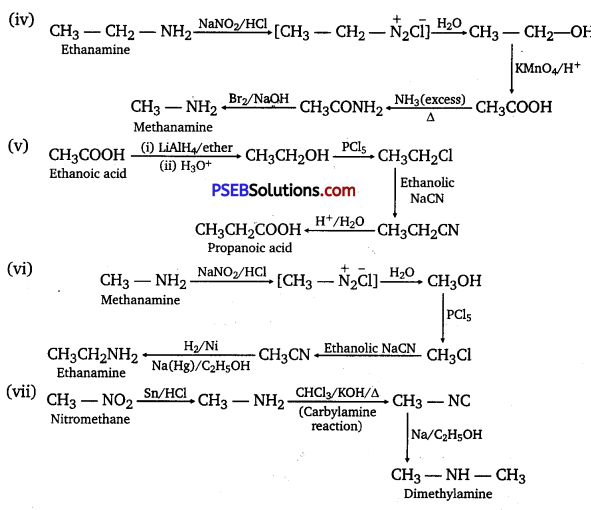
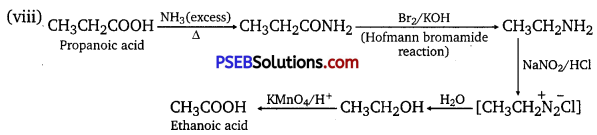
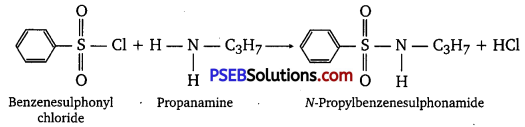
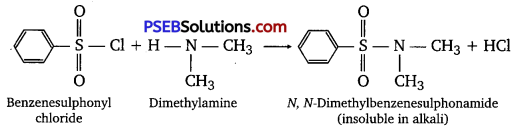
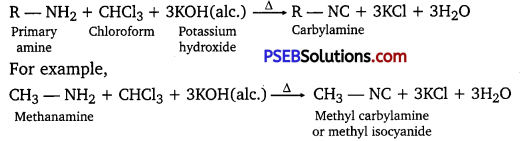
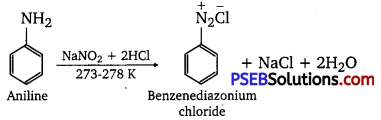
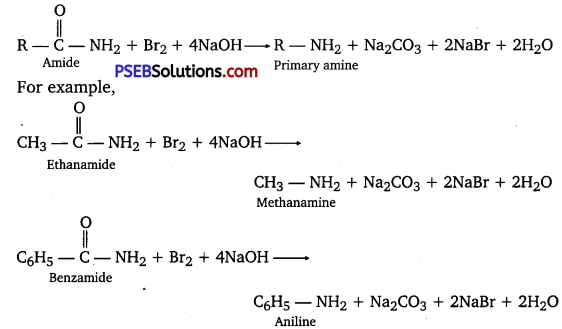
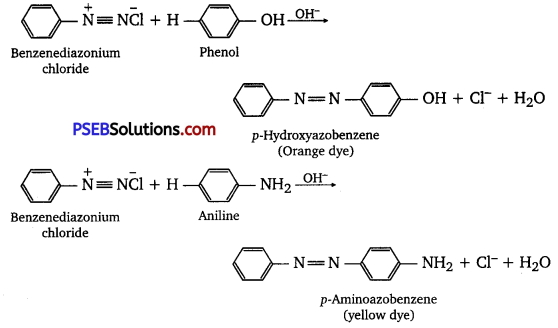
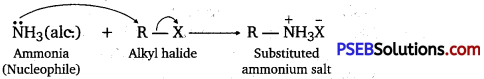
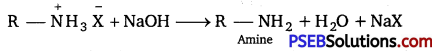




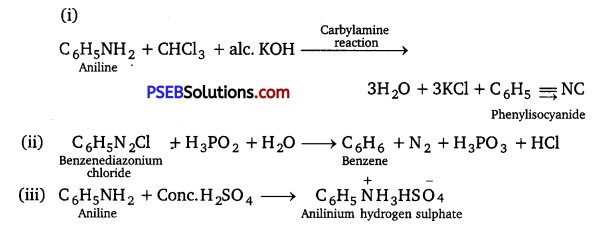
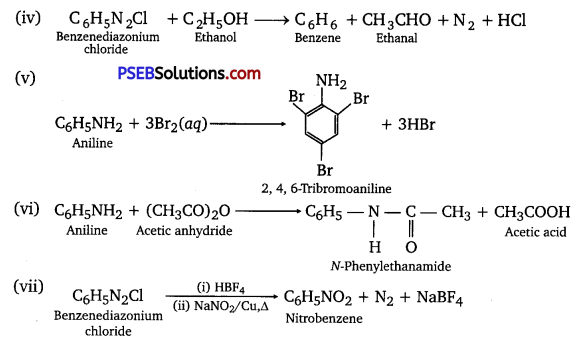
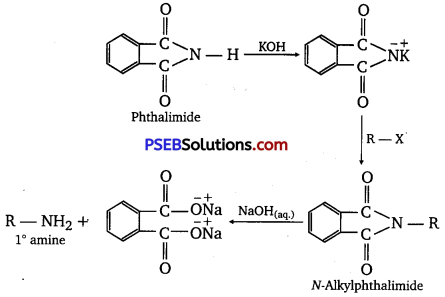

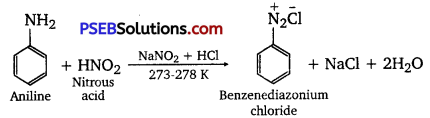
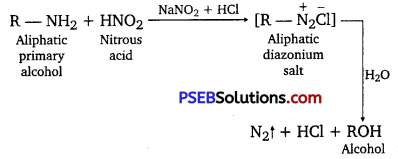
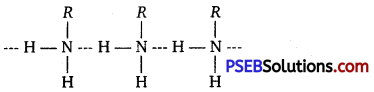
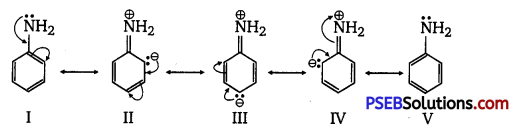
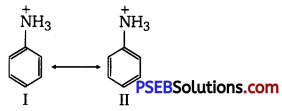



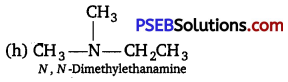


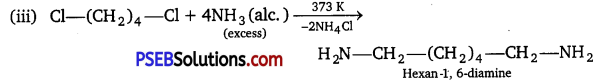
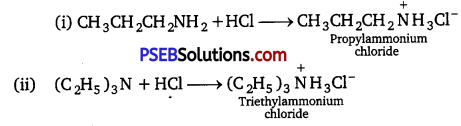
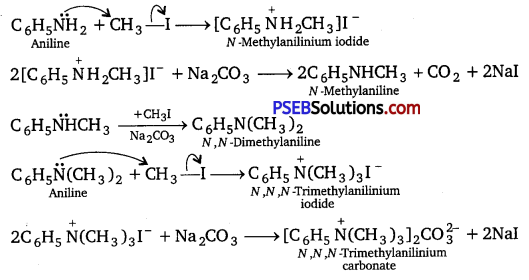




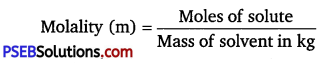
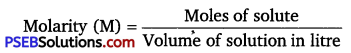
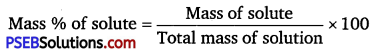
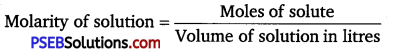

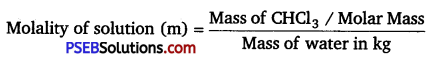


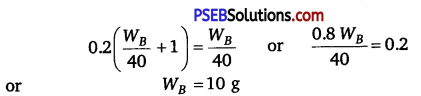

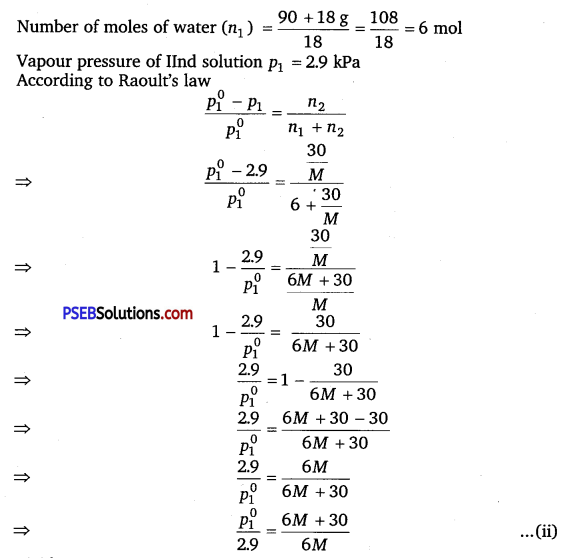


 has polar -OH group and can form H-bond. Thus, it is highly soluble in water.
has polar -OH group and can form H-bond. Thus, it is highly soluble in water.