Bhagya

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 6 Application of Derivatives Ex 6.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.5

Question 1.
Find the maximum and minimum values, if any, of the following functions given by
(i) = (2x – 1)² + 3
(ii) f(x) = 9x² + 12x + 2
(iii) f(x) = – (x – 1)² + 10
(iv) g(x) = x³ + 1
Solution.
(i) The given function is f(x) = (2x – 1)² + 3.
It can be observed that (2x – 1)² ≥ 0 for every x ∈ R.

Therefore, f(x) = (2x – 1)² + 3 ≥ 3 for every x ∈ R.
The minimum value of f is attained when 2x – 1 = 0
⇒ x = \(\frac{1}{2}\)
∴ Minimum value of f = f(\(\frac{1}{2}\))
= (2 . \(\frac{1}{2}\) – 1)² + 3 = 3
Hence, function f does not have a maximum value.

(ii) The given function is f(x) = 9x² + 12x + 2
= (3x + 2)² – 2
It can be observed that (3x + 2)² ≥ 0 for every x ∈ R.
Therefore, f(x) = (3x + 2)² – 2 ≥ – 2 for every x ∈ R.
The minimum value of f is attained when 3x +2 = 0
⇒ x = \(\frac{-2}{3}\)
∴ Minimum value of f = f(\(\frac{-2}{3}\))= (3 . (\(\frac{- 2}{3}\)) + 2)² – 2 = – 2.
Hence, function f does not have a maximum value.

(iii) The given function is f(x) = -(x – 1)² + 10.
It can be observed that (x – 1)² ≥ 0 for every x ∈ R.
Therefore, f(x) = – (x – 1)² + 10 ≤ 10 for every x ∈ R.
The minimum value off is attained when (x – 1) = 0
⇒ x = 1
∴ Minimum value of f = f(1) = -(1 – 1)² + 10 = 10
Hence, function f does not have a minimum value.

(iv) The given function is g(x) = x³ + 1.
We observe that the value of f(x) increases when the value of x increases and f(x) can be made as large as we please by giving large value to x. So, f(x) does not have the maximum value.
Similarly, f(x) can be made as small as we please by giving smaller values of x.
So, f(x) does not have the minimum value.

Question 2.
Find the maximum and minimum values, if any, of the following functions given by
(i) f(x) = |x + 2| – 1
(ii) g(x) = – |x + 1| + 3
(iii) h(x) = sin (2x) + 5
(iv) f(x) = |sin 4x| + 3|
(v) h(x) = x + 1, x e (-1, 1)
Solution.
(i) Given, f(x) = |x + 2 | – 1
We know that, | x + 2 | ≥ 0 for every x ∈ R.
Therefore, f(x) = |x + 2| – 1 ≥ – 1 for every x ∈ R.
The minimum value of / is attained when | x + 2| = 0
⇒ x = – 2
∴ Minimum value of f = f(- 2) = = |- 2 + 2| – 1 = – 1
Hence, function f does not have a maximum value.

(ii) Given, g(x) = – | x + 1| + 3
We know that -| x + 1| < 0 for every x ∈ R.
Therefore, g(x) = -|x + 1| + 3 ≤ 3 for every x ∈ R.
The maximum value of g is attained when |x + 1| = 0
⇒ x = – 1
∴ Maximum value of g = g(- 1) = -|- 1 + 1| + 3 = 3
Hence, function g does not have a minimum value.

(iii) Given, h(x) = sin 2x + 5
We know that, – 1 ≤ sin 2x ≤ 1
⇒ – 1 + 5 ≤ sin 2x + 5 ≤ 1 + 5
⇒ 4 ≤ sin 2x + 5 ≤ 6
Hence, the maximum and minimum values of h are 6 and 4, respectively.

(iv) Given,f(x) = |sin 4x + 3|
We know that, – 1 < sin 4x < 1
⇒ 2 ≤ sin 4x + 3 ≤ 4
2 ≤ |sin 4x + 3| ≤ 4
Hence, the maximum and minimum values of f are 4 and 2, respectively.

(v) h(x) = x + 1, x ∈ (- 1, 1)
Here, if a point x₀ is closest to – 1, then we find \(\frac{x_{0}}{2}\) + 1 < x₀ ∈ (- 1, 1).
Also, if x₁ is closest to 1, then
x₁ + 1 < \(\frac{x_{1}+1}{2}\) + 1 for all x₁ ∈ (- 1, 1).
Hence, function h(x) has neither maximum nor minimum value in (- 1, 1).

Question 3.
Find the local maxima and local minima, if any, of the following functions, Find also the local maximum and the local minimum values, as the case may be :
(i) f(x) = x²
(ii) g(x) = x³ – 3x
(iii) h(x) = sin x + cos x, 0 < x < \(\frac{\pi}{2}\)
(iv) f(x) = sin x – cos x, 0 < x < 2π
(v) f(x) = x³ – 6x² + 9x + 15
(vi) g(x) = \(\frac{x}{2}+\frac{2}{x}\), x > 0
(vii) g(x) = \(\frac{1}{x^{2}+2}\)
(viii) f(x) = \(x \sqrt{1-x}\), x > 0
Solution.
(i) Given, f(x) = x²
⇒ f'(x) = 2x
Now, f'(x) = 0
⇒ x = 0
Thus, x = 0 is the only critical point which could possibly be the point of local maxima or local minima of f.
We have f”(0) = 2, which is positive.
Therefore, by second derivative test, x = 0 is a point of local minima and local minimum value of f at x = 0 is f(0) = 0.

(ii) Given, g(x) = x³ – 3x
⇒ g'(x) = 3x² – 3
Now, g'(x) = 0
⇒ 3x² = 3
⇒ x = ± 1
∴ g'(x) = 6x
⇒ g'(1) = 6 > 0
⇒ g'(- 1) = – 6 > 0
By second derivative test x = 1 is a point of local minima and local minimum value of g at x = 1 is
g(1) = 1³ – 3
= 1 – 3 = – 2.
However, x = – 1 is a point of local maxima and local maximum value of g at x = – 1 is
g(- 1) = (- 1)³ – 3(- 1)
= – 1 + 3 = 2.

(iii) Given, h(x) = sinx + cos x, 0 < x < \(\frac{\pi}{2}\)
∴ h'(x) = – sin x – cos x = -(sin x + cos x)
h'(x) = 0
⇒ sin x = cos x
⇒ tan x = 1
⇒ x = \(\frac{\pi}{4}\) ∈ (0, \(\frac{\pi}{2}\))
h”(x) = – sin x – cos x
= – (sin x + cos x)
h(\(\frac{\pi}{4}\)) = – \(\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\right)=-\frac{2}{\sqrt{2}}=-\sqrt{2}<0\)
Therefore, by second derivative test, x = \(\frac{\pi}{4}\) is a point of local maxima and
and the local maximum value of h at x = \(\frac{\pi}{4}\) is h(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) = √2.

(iv) f(x) = sin x – cos x, 0 < x < 2π
∴ f'(x) = cos x + sin x f'(x) = 0
⇒ cos x = – sin x ⇒ tan x = 1
⇒ x = \(\frac{3 \pi}{4}\), \(\frac{7 \pi}{4}\) ∈ (0, 2π)
f”(x) = – sin x + cos x f”(\(\frac{3 \pi}{4}\)) = \(-\sin \frac{3 \pi}{4}+\cos \frac{3 \pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}>0\)

f”(\(\frac{7 \pi}{4}\)) = \(-\sin \frac{7 \pi}{4}+\cos \frac{7 \pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}>0\)

Therefore, by second derivative test, x = \(\frac{3 \pi}{4}\) is a point of local maxima and the local maximum value of f at x = \(\frac{3 \pi}{4}\) is
f(\(\frac{3 \pi}{4}\)) = sin \(\frac{3 \pi}{4}\) – cos \(\frac{3 \pi}{4}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) = √2.

However, x = \(\frac{7 \pi}{4}\) is a point of local minima and the local minimum value of f at x = \(\frac{7 \pi}{4}\) is
f(\(\frac{7 \pi}{4}\)) = sin \(\frac{7 \pi}{4}\) – cos \(\frac{7 \pi}{4}\)
= \(-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}\)

(v) Given, f(x) = x³ – 6x² + 9x + 15
f'(x) = 3x² – 12x + 9
f'(x) = 0
⇒ 3(x² – 4x + 3) = 0
⇒ 3(x – 1) (x – 3) = 0
⇒ x = 1, 3
Now, f'(x) = 6x – 12 = 6 (x – 2)
f'(1) = 6(1 – 2) = – 6 < 0 ⇒ f'(3) = 6(3 – 2) = 6 > 0
Therefore, by second derivative test, x = 1 is a point of local maxima and the local maximum value of f at x = 1 is
f(1) = 1 – 6 + 9 + 15 = 19.
However, x = 3 is a point of local minima and the local minimum value of f at x = 3 is
f(3) = 27 – 54 + 27 + 15 = 15

(vi) Given, g(x) = \(\frac{x}{2}+\frac{2}{x}\), x > 0

∴ g'(x) = \(\frac{1}{2}-\frac{2}{x^{2}}\)

Now, g'(x) = 0 gives \(\frac{2}{x^{2}}=\frac{1}{2}\)
⇒ x² = 4
⇒ x = ± 2
Therefore, by second derivative test, x = 2 is a point of local minima and the local minimum value of g at x = 2 is
g(2) = \(\frac{2}{2}+\frac{2}{2}\) = 1 + 1 = 2.

(vii) Given, g(x) = \(\frac{1}{x^{2}+2}\)

∴ g'(x) = \(\frac{-(2 x)}{\left(x^{2}+2\right)^{2}}\)
Now, g'(x) = 0
⇒ \(\frac{-2 x}{\left(x^{2}+2\right)^{2}}\) = 0
⇒ x = 0
Now, for values close to x = 0 and to the left of 0, g’(x) > 0.
Also, for values close to x = 0 and to the right of 0, g’(x) < 0.
Therefore, by first derivative test, x = 0 is a point of local maxima and the local maximum value of g(0) is \(\frac{1}{0+2}=\frac{1}{2}\).

(viii) Given, f(x) = x\(\sqrt{1-x}\)

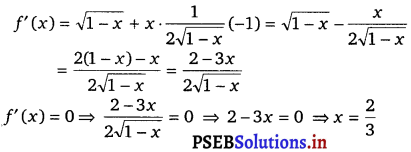
Therefore, by second derivative test, x = \(\frac{2}{3}\) is a point of local maxima and the local maximum value of f at x = \(\frac{2}{3}\) is
f(\(\frac{2}{3}\)) = \(\frac{2}{3} \sqrt{1-\frac{2}{3}}=\frac{2}{3} \sqrt{\frac{1}{3}}=\frac{2}{3 \sqrt{3}}=\frac{2 \sqrt{3}}{9}\).

Question 4.
Prove that the following functions do not have maxima or minima:
(i) f(x) = e^x
(ii) g(x) = log x
(iii) h(x) = x³ + x² + x + 1
Solution.
(i) Given function is f(x) = e^x
⇒ f'(x) = e^x
Now, if f'(x) = 0, then e^x = 0.
But, the exponential function can never assume 0 for any value of x. ,
Therefore, there does not exist c ∈ R such that f'(c) = 0.
Hence, function f does not have maxima or minima.

(ii) Given function is g(x) = log x
⇒ g'(x) = \(\frac{1}{x}\)
Since, log x is defined for a positive number x, g’ (x) > 0 for any x.
Therefore, there does not exist ce R such that g’ (c) = 0.
Hence, function g does not have maxima or minima.

(iii) Given function is h(x) = x³ + x² + x + 1
⇒ h'(x) = 3x + 2x + 1
Now, h(x) = 0
⇒ 3x² + 2x +1 = 0
⇒ x = \(\frac{-2 \pm 2 \sqrt{2} i}{6}=\frac{-1 \pm \sqrt{2} i}{3}\) ∉ R
Therefore, there does not exist c ∈ R such that h'(c) = 0.
Hence, function h does not have maxima or minima.

Question 5.
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals :
(i) f(x) = x³, x ∈ [- 2, 2]
(ii) f(x) = sin x + cos x, x ∈ [0, π]
(iii) f(x) = 4x – \(\frac{1}{2}\) x², x ∈ [- 2, \(\frac{9}{2}\)]
(iv) f(x) = (x – 1)² + 3, x ∈ [- 3, 1]
Solution.
(i) The given function is f(x) = x³
∴ f'(x) = 3x²
Now, f(x) = 0
⇒ x = 0
Then, we evaluate the value of f at critical point x = 0 and at end points of the interval [- 2, 2].
∴ f(0) = 0; f(- 2) = (- 2) 3 = – 8; 012f(2) = (2)³ – 8
Hence, we can conclude that the absolute maximum value of f on [- 2, 2] is 8 occurring at x = 2.
Also, the absolute minimum value of f on [- 2, 2] is – 8 occurring at x = – 2.

(ii) The given function is f(x) = sin x + cos x.
f'(x) = cos x – sin x
Now, f'(x) = 0
⇒ sin x = cos x
⇒ tan x = 1
⇒ x = \(\frac{\pi}{4}\)
Then, we evaluate the value of f at critical point x = \(\frac{\pi}{4}\) and at the end points of the interval [0, π].

∴ f(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}+\frac{2}{\sqrt{2}}=\sqrt{2}\)

f(0) = sin 0 + cos 0 = 0 + 1 = 1
f(π) = sin π + cos π = 0 – 1 = – 1
Hence, we can conclude that the absolute maximum value of f on [0, π] is 2 occurring at x = \(\frac{\pi}{4}\) and the absolute minimum value of f on [0, π] is – 1 occurring at x = π.

(iii) The given function is f(x) = 4x – \(\frac{1}{2}\) x²
f(x) = 4 – \(\frac{1}{2}\) (2x) = 4 – x
Now, f'(x) = 0
⇒ x = 4
Then, we evaluate the value of f at critical point x = 4 and at the end [- 2, \(\frac{9}{2}\)]
∴ f(4) = 16 – \(\frac{1}{2}\) (16) = 16 – 8 = 8

f(- 2) = – 8 – \(\frac{1}{2}\) (4) = – 8 – 2 = – 10

f(\(\frac{1}{2}\)) = \(4\left(\frac{9}{2}\right)-\frac{1}{2}\left(\frac{9}{2}\right)^{2}=18-\frac{81}{8}\)

= 18 – 10.125 = 7.875
Hence, we can conclude that the absolute maximum value of f on is 8 occurring at x = 4 and the absolute minimum value of f on – 10 occurring at x = – 2.

(iv) The given function is f(x) = (x – 1)² + 3
∴ f'(x) = 2(x – 1)
Now, f'(x) = 0
⇒2 (x – 1) = 0
⇒ x = 1
Then, we evaluate the value of f at critical point x = 1 and at the end points of the interval [- 3, 1].
∴ f(1) = (1 – 1)² + 3 = 0 + 3 = 3;
f(- 3) = (- 3 – 1)² + 3 = 16 + 3 = 19
Hence, we can conclude that the absolute maximum value of / on [- 3, 1] is 19 occurring at x = – 3 and the minimum value of f on [- 3, 1] is 3 occurring at x = 1.

Question 6.
Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 – 72x – 18x²
Solution.
The profit function is given as p(x) = 41 – 72x – 18x²
On differentiating both sides w.r.t. x, we get
p'(x) = – 72 – 36x = – 36 (2 + x)
Again, differentiating both sides w.r.t. x, wt ,et
p”(x) = – 36
For maxima or minima, put p(x) = 0
⇒ – 36 (2 + x) = 0
⇒ x + 2 = 0
⇒x = – 2
At x = – 2, p'(-2) = – 36 < 0
∴ x = – 2 is a point of maxima.
Maximum profit, p(- 2) = 41 – 72 (- 2) – 81 (- 2)²
= 41 + 144 – 72 = 113
Hence, the maximum profit that a company can make, is 113 units.

Question 7.
Find both the maximum value and the minimum value of 3x⁴ – 8x³ + 12x² – 48x + 25 on the interval [0, 3].
Solution.
Let f(x) = 3x⁴ – 8x³ + 12x² – 48x + 25
⇒ f'(x) = 12x³ – 24x² + 24x – 48
= 12 (x³ – 2x² + 2x – 4)
= 12 (x² (x – 2) + 2 (x – 2))
= 12(x – 2) (x² + 2)
For maxima or minima put f'(x) = 0
12(x – 2) (x² + 2) = 0
⇒ if x – 2 = 0 ⇒ x = 2 e [0, 3]
And if, x² + 2 = 0
⇒ x² = – 2
⇒x = √- 2
Hence, the only real root is x = 2 which is considered as critical point.
Now, we evaluate the value of f at critical point x = 2 and at the end point of the interval [0, 3].
At x = 2, f(2) = 3 × 2⁴ – 8 × 2³ + 12 × 2² – 48 × 2 + 25
= 48 – 64 + 48 – 96 + 25 = – 39

At x = 0, f(0) = 0 – 0 + 0 – 0 + 25 = 25
At x = 3, f(3) = 3 × 3⁴ – 8 × 3³ + 12 × 3² – 48 × 3 + 25
= 243 – 216 + 108 – 144 + 25 = 16
Hence, we can conclude that the absolute maximum value of f is 25 at x = 0 and the absolute minimum value of f is – 39 at x = 2.

Question 8.
At what points in the interval [0, 2π], does the function sin2x attain its maximum value?
Solution.
Let f(x) = sin 2x
⇒ f'(x) = 2 cos 2x
Now, f'(x) = 0
⇒ cos 2x = 0
⇒ 2x = \(\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \frac{7 \pi}{2}\)

⇒ x = \(\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}\)

Then, we evaluate the value off at critical points x = \(\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}\) and at the end points of the interval [0, 2π].
f(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{2}\) = 1;

f(\(\frac{3 \pi}{4}\)) = sin \(\frac{3 \pi}{2}\) = – 1;

f(\(\frac{5 \pi}{4}\)) = sin \(\frac{5 \pi}{2}\) = 1;

f(\(\frac{7 \pi}{4}\)) = sin \(\frac{7 \pi}{2}\) = – 1;

f(0) = sin 0 = 0;
f(2π) = sin 2π = 0
Hence, we can conclude that the absolute maximum value of f on [0, 2π] is occurring at x = \(\frac{\pi}{4}\) and x = \(\frac{5 \pi}{4}\).

Question 9.
What is the maximum value of the function sin x + cos x?
Solution.
Let f(x) = sin x + cos x
f”(x) = – sin x – cos x = – (sin x + cos x)
Now, f”(x) will be negative when (sin x + cos x) is positive i.e., when sin x and cos x are both positive.
Also, we know that, sin x and cos x both are positive in the first quadrant.
Then, f”(x) will be negative when x ∈ (0, \(\frac{\pi}{2}\))
Thus, we consider x = \(\frac{\pi}{4}\)

f”(\(\frac{\pi}{4}\)) = – (sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\))

= –\(\left(\frac{2}{\sqrt{2}}\right)\) = – √2
∴ By second derivative test, f will be the maximum at x = \(\frac{\pi}{4}\) and the maximum value of f is
f(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\).

Question 10.
Find the maximum value of 2x³ – 24x + 107in the interval [1, 3]. Find the maximum value of the same function in [- 3, – 1].
Solution.
Let f(x) = 2x³ – 24x + 107
⇒ f(x) = 6x² – 24
= 6(x² – 4)
Now, f'(x) = 0
⇒ 6 (x² – 4) = 0
⇒ x² = 4
⇒ x = ± 2
We first consider the interval [1, 3]
Then, we evaluate the value of f at the critical point x = 2 ∈ [1, 3] and at the end points of the interval [1, 3].
f(2) = 2(8) – 24(2) +107 = 16 – 48 +107 = 75
f(1) = 2(1)-24(1)+ 107 = 2 – 24 +107 = 85
f(3) = 2(27) – 24(3) +107 = 54 – 72 +107 = 89
Hence, the absolute maximum value of f(x) in the interval [1, 3] is 89 occurring at x = 3.
Next, we consider the interval [- 3, – 1],
Evaluate the value of f at the critical point x = – 2 ∈ [- 3, – 1] and at the end points of the interval [1, 3].
f(- 3) = 2(- 27) – 24(- 3) +107 = – 54 + 72 +107 = 125
f(- 1) = 2(- 1) – 24(- 1) + 107 = – 2 + 24 +107 = 129
f(- 2) = 2(- 8) – 24(- 2) + 107 = – 16 + 48 +107 = 139
Hence, the absolute maximum value of f(x) in the interval [- 3, – 1] is 139 occurring at x = – 2.

Question 11.
It is given that at x = 1, the function x⁴ – 62x² + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
Solution.
Let f(x) = x⁴ – 62x² + ax + 9
f'(x) = 4x³ – 124x + a
It is given that function f attains its maximum value on the interval [0, 2] at x = 1.
∴ f'(1) = 0
⇒ 4 – 124 + a = 0
⇒ a = 120
Hence, the value of a is 120.

Question 12.
Find the maximum and minimum values of x + sin 2x on [0, 2π].
Solution.
Let f(x) = x + sin 2x
⇒ f'(x) = 1 + 2 cos 2x
Now, f'(x) = 0
⇒ cos 2x = – \(\frac{1}{2}\) = – cos \(\frac{\pi}{3}\)

= cos (π – \(\frac{\pi}{3}\))

= cos \(\frac{2 \pi}{3}\)

2x = 2n ± \(\frac{2 \pi}{3}\), n ∈ Z

x = nπ ± \(\frac{\pi}{3}\), n ∈ Z
⇒ x = \(\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}\) ∈[0, 2π]

Then, we evaluate the value of f at critical points x = \(\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}\) and at the end points of the interval [0, 2π],
∴ f(\(\frac{\pi}{3}\)) = \(\frac{\pi}{3}+\sin \frac{2 \pi}{3}=\frac{\pi}{3}+\frac{\sqrt{3}}{2}\);

f(\(\frac{2 \pi}{3}\)) = \(\frac{2 \pi}{3}+\sin \frac{4 \pi}{3}=\frac{2 \pi}{3}-\frac{\sqrt{3}}{2}\);

f(\(\frac{4 \pi}{3}\)) = \(\frac{4 \pi}{3}+\sin \frac{8 \pi}{3}=\frac{4 \pi}{3}+\frac{\sqrt{3}}{2}\);

f(\(\frac{5 \pi}{3}\)) = \(\frac{5 \pi}{3}+\sin \frac{10 \pi}{3}=\frac{5 \pi}{3}-\frac{\sqrt{3}}{2}\);
f(0) = 0 + sin 0 = 0;
f(2π) = 2π + sin 4π = 2π + 0 = 2π
Thus, maximum value is 2π at x = 2π and minimum value is 0 at x = 0.

Question 13.
Find two numbers whose sum is 24 and whose product is as large as possible.
Solution.
Let one number be x.
Then, the other number is (24 – x).
Let f(x) denote the product of the two numbers.
Thus, we have P(x) = x(24 – x) = 24x – x²
P'(x) = 24 – 2x;
P”(x) = – 2
Now, P’ (x) = 0
⇒ x =12
Also, P”(12) = – 2 < 0
By second derivative test, x = 12 is the point of local maxima of P.
Hence, the product of the number is the maximum when the numbers are 12 and 24 – 12 = 12.

Question14.
Find two positive numbers x and y such that x + y = 60 and xy³ is maximum.
Solution.
The two numbers are x and y such that x + y – 60
⇒ y = 60 – x
Let f(x) = xy³
⇒ f(x) = x(60 – x)³
⇒ f'(x) = (60 – x)³ – 3x (60 – x)²
= (60 – x)² [60 – x – 3x]
= (60 – x)² (60 – 4x)
Also, f(x) = – 2 (60 – x) (60 – 4x) – 4 (60 – x)²
= – 2 (60 – x) [60 – 4x + 2(60 – x)]
= – 2 (60 – x) (180 – 6x)
= -12(60 – x) (30 – x)
Now, f'(x) = 0
⇒ x = 60 or x = 15
When, x = 60 then, f”(x) = 0
When x = 15, then f'(x) – 12(60 – 15) (30 – 15) = – 12 × 45 × 15 < 0 .
∴ By second derivative test, x = 15 is a point of local maxima of f.
Thus, function xy³ is maximum when x = 15 and y = 60 -15 = 45.
Hence, the required numbers are 15 and 45.

Question 15.
Find two positive numbers x and y such that their sum is 35 and the product x²zy⁵ is a maximum.
Solution.
Let one number be x. Then, the other number is y = (35 – x).
Let P(x) = x²y⁵, then
P(x) = x² (35 – x)⁵
∴ P'(x) = 2x (35 – x)⁵ – 5x² (35 – x)⁴
= x (35 – x)⁴ [2(35 – x) – 5x]
= x (35 – x)⁴ (70 – 7x)
= 7x (35 – x)4^{4/sup> (10 – x)}

And p”(x) = 7(35 – x)⁴ (10 – x) + 7x [- (35 – x)⁴ – 4(35 – x)³ (10 – x)]
= 7 (35 – x)⁴ (10 – x) – 7x (35 – x)⁴ – 28x (35 – x)³ (10 – x)
= 7 (35 – x)³ [(35 – x)(10 – x) – x(35 – x) – 4x(10 – x)]
= 7 (35-x)³ [350 – 45x + x² – 35x + x² – 40x + 4x²]
= 7 (35 – x)³ (6x² – 120x + 350)
Now, P'(x) = 0
⇒ x = 0, x = 35, x = 10
When, x = 35, f'(x) = f(x) = 0 and y = 35 – 35 = 0.
This will make the product x²y⁵ equal to 0.
When x = 0, then y = 35 -0 = 35 and the product x2y2 will be 0.
∴ x = 0 and x = 35 cannot be the possible values of x.
When x = 10 then, we have
P'(x) = 7(35 – 10)³ (6 × 100 – 120 × 10 + 350)
= 7(25)³ (- 250) < 0
∴ By second derivative test, P(x) will be the maximum when x = 10 and y = 35 – 10 = 25.
Hence, the required numbers are 10 and 25.

Question 16.
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Solution.
Let one number be x.
Then, the other number is (16 – x).
Let the sum of the cubes of these numbers be denoted by S(x). Then, S(x) = x3 + (16 -x)3
∴ S'(x) = 3x² – 3(16 – x)²;
S'(x) = 6x + 6(16 – x)
Now, S'(x) = 0
⇒ 3x² – 3(16 – x)² = 0
⇒ x² – (16 – x)² = 0
⇒ x² – 256 – x² + 32x = 0
⇒ x =\(\frac{256}{32}\) = 8
Now, S'(8) = 6(8) + 6(16 -8) = 48 + 48 = 96 > 0.
By second derivatives test, x = 8 is the point of local minima of S.
Hence, the sum of the cubes of the numbers is the minimum when the numbers are 8 and 16 – 8 = 8.

Question 17.
A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Solution.

Let the side of the square to be cut-off be x cm (0 < x < 9).
Then, the length and the breadth of the box will be (18 – 2x) cm each and the height of the box is x cm.
Let V the volume of the open box formed by folding up the flaps, then
V = x (18 – 2x) (18 – 2x)
= 4x (9 – x)²
= 4x (81 + x² – 18x)
= 4(x³ – 18x² + 81x)
On differentiating twice w.r.t. x, we get
\(\frac{d V}{d x}\) = 4(3x² – 36x + 81)
= 12(x² – 12x+27)
and \(\frac{d^{2} V}{d x^{2}}\) = 12 (2x – 12) = 24 (x – 6)
For maxima put \(\frac{d V}{d x}\) = 0
⇒ 12(x – 12x + 27) = 0
⇒ x² – 12x + 27 = 0
⇒ (x – 3) (x – 9) = 0
⇒ x = 3, 9
But x = 9 is not possible,
∵ 2x = 2 × 9 = 18
Which is equal to side of square piece.
At x = 3,
\(\left(\frac{d^{2} V}{d x^{2}}\right)_{x=3}\) = 24 (3 – 6) = – 72 < 0

∴ By second derivative test, x = 5 is the point of maxima.
Hence, the side of the square to be cut-off to make the volume of the box maximum possible is 5 cm.

Question 18.
A rectangular sheet of tin 45cm by 24cm is to be made into a box without top, by cutting off square from each comer and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Solution.

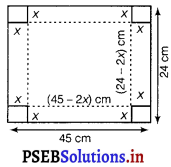
Let the side of the square to be cut off be x cm.
Then, the height of the box is x, the length is 45 – 2x and the breadth is 24 f'(x) 2x.
Let V be the corresponding volume of the box then,
V = x (24 – 2x) (45 – 2x)
V = x (4x² – 138x + 1080)
=4x³ – 138 x² + 1080x
On differentiating twice w.r.t. x,

\(\frac{d V}{d x}\) = 12x² – 276x + 1080

\(\frac{d^{2} V}{d x^{2}}\) = 24x – 276
For maxima put \(\frac{d V}{d x}\) = o
⇒ 12x² – 276x + 1080 = 0
⇒ x² – 23x + 90 = 0
= (x – 18) (x – 5) = 0
⇒ x = 5, 18
It is not possible to cut-off a square of side 18 cm from each corner of the rectangular sheet.
Thus, x cannot be equal to 18.
At x = 5,
\(\left(\frac{d^{2} V}{d x^{2}}\right)_{x=5}\) = 24 × 5 – 276
= 120 – 276
= – 156 < 0
∴ By second derivative test, x = 5 is the point of maxima.
Hence, the side of the square to be cut-off to make the volume of the box maximum possible is 5 cm.

Question 19.
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Solution.
Let a rectangle of length l and breadth b be inscribed in the given circle of radius a.
Then, the diagonal passes through the centre and is of length 2a cm.

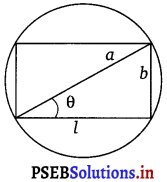
Now, by applying the Pythagoras theorem, we have (2 a)² = l² + b²
⇒ b² = 4 a² – l²
⇒ b = \(\sqrt{4 a^{2}-l^{2}}\)
∴ Area of rectangle, A = l \(\sqrt{4 a^{2}-l^{2}}\)

∴ By the second derivative test, when l = √2a then the area of the rectangle is the maximum.
Since, l = b = √2a, therefore the rectangle is a square.
Hence, it has been proved that of all the rectangles inscribed in the given fixed circle the square has the maximum area.

Question 20.
Show that th right circular cylinder of given surface and maximum volume Is such that its heigh is equal to the diameter of the base.
Solution.

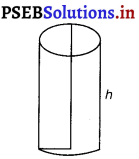
Let r and h be the radius and height of the cylinder, respectively.
Then, the surface area (S) of the cylinder is given by
S = 2πr² + 2πrh
⇒ h = \(\frac{S-2 \pi r^{2}}{2 \pi r}=\frac{S}{2 \pi}\left(\frac{1}{r}\right)-r\)

Let V be the volume of the cylinder. Then,

V = πr²h
= πr² \(\left[\frac{S}{2 \pi}\left(\frac{1}{r}\right)-r\right]=\frac{S r}{2}-\pi r^{3}\)

On differentiating w.r.t. x, we get
\(\frac{d V}{d r}=\frac{S}{2}-3 \pi r^{2}\)

For maxima or mmima put \(\frac{d V}{d r}\) = 0
\(\frac{S}{2}\) = 3πr²
r² = \(\frac{S}{6 \pi}\)

Now, \(\frac{d^{2} V}{d r^{2}}\) = – 6π \(\left(\sqrt{\frac{S}{6 \pi}}\right)\) < 0

∴ By second derivative test, the volume is the maximum when r² = \(\frac{S}{6 \pi}\).

Now, when r² = \(\frac{S}{6 \pi}\), then h = \(\frac{6 \pi r^{2}}{2 \pi}\left(\frac{1}{r}\right)\) – \(\frac{1}{r}\) = 3r – r = 2r.
Hence, the volume is the maximum when the height is twice the radius si.e., when the height is equal to the diameter.

Question 21.
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic cm, find the dimensions of the can which has the minimum surface area?
Solution.

 

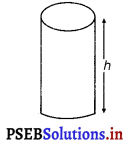
Let r and h be the radius and height of the cylinder, respectively.
Then, volume (V) of the cylinder is given by
V = πr²h = 100
∴ h = \(\frac{100}{\pi r^{2}}\)
Surface area (S) of the cylinder is given by S = 2πr² + 2πrh = 2πr² + \(\frac{200}{r}\)
On differentiating w.r.t. x, we get h
∴ \(\frac{d S}{d r}\) = 4πr – \(\frac{200}{r^{2}}\)
Now, for maxima or minima put \(\frac{d S}{d r}\) = 0

⇒ 4πr = \(\frac{200}{r^{2}}\)

⇒ r³ = \(\frac{200}{4 \pi}=\frac{50}{\pi}\)

⇒ r = \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\)

Again, differentiating w.r.t. x, we get.
\(\frac{d^{2} S}{d r^{2}}\) = 4π + \(\frac{400}{r^{3}}\)

Now, it is observed that when r = latex]\left(\frac{50}{\pi}\right)^{\frac{1}{3}}[/latex], \(\frac{d^{2} S}{d r^{2}}\) > 0.

∴ By second derivative test, the surface area is the minimum when the radius of the cylinder is \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) cm.

when r = \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\), then h = \(\frac{100}{\pi\left(\frac{50}{\pi}\right)^{\frac{2}{3}}}=2\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) cm

Hence, the required dimensions of the can which has the minimum surface area, is given by radius = \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) cm and height = 2 \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) cm.

Question 22.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Solution.
Let a piece of length l be cut from the given wire to make a square.
Then, the other piece of wire to be made into a circle is of length (28 – l) m.
Now, side of square = \(\frac{l}{4}\)
Let r be the radius of the circle. Then, 2πr = 28 – l
The combined area of the square and the circle (A) is given by A = (side of the square)² + πr²

∴ By second derivative test, the area (A) is the minimum when l = \(\frac{112}{\pi+4}\)

Hence, the combined area is the minimum when the length of the wire in making the square is \(\frac{112}{\pi+4}\) cm while the length of the wire in making the circle is 28 – \(\frac{112}{\pi+4}=\frac{28 \pi}{\pi+4}\) cm.

Question 23.
Prove that the volume of the largest cone that can be inscribed in a sphere of radius R, is \(\frac{8}{27}\) of the volume of the sphere.
Solution.
Let r and h be the radius and height of the cone respectively inscribed in a sphere of radius R.
Let V be the volume of the cone.
Then, V = \(\frac{1}{3}\) πr²h
Height of the cone is given by h = R + AB
= R + \(\sqrt{R^{2}-r^{2}}\) [∵ ABC is right angled triangle]

For maxima put
\(\frac{d V}{d r}\) = 0

⇒ \(\frac{2}{3}\) πrR = \(\frac{3 \pi r^{3}-2 \pi r R^{2}}{3 \sqrt{R^{2}-r^{2}}}\)

⇒ 2R = \(\frac{3 r^{2}-2 R^{2}}{\sqrt{R^{2}-r^{2}}}\)

⇒ 2R \(\sqrt{R^{2}-r^{2}}\) = (3r² – 2R²)²
⇒ 4R² (R² – r²)
= (3r² – 2R²)²
⇒ 4R⁴ – 4R²r² = 9r⁴ + 4R⁴ – 12r²R²
⇒ 9r⁴ = 8R²r²
⇒ r² = \(\frac{8}{9}\) R²

∴ By second derivative test, the volume of the cone is the maximum when r² = \(\frac{8}{9}\) R².

When r² = \(\frac{8}{9}\) R², then
h = R + \(\sqrt{R^{2}-\frac{8}{9} R^{2}}=R+\sqrt{\frac{1}{9} R^{2}}=R+\frac{R}{3}=\frac{4}{3} R\)

Therefore, V = \(\frac{1}{3} \pi\left(\frac{8}{9} R^{2}\right)\left(\frac{4}{3} R\right)=\frac{8}{27}\left(\frac{4}{3} \pi R^{3}\right)\)

= \(\frac{8}{27}\) × (volume of the sphere)
Hence, the volume of the largest cone that can be inscribed in the sphere, is \(\frac{8}{27}\) of the volume of the sphere.

Question 24.
Show that the right circular cone of least curved surface and given volume has an altitude equal toJ time the radius of the base.
Solution.
Let r be the radius of the base, h be the height, V be the volume and S be the curved surface area of the cone.
Then, V = \(\frac{1}{3}\) πr²h
⇒ 3V = πr²h
⇒ 9V² = π² r⁴ h²
⇒ h² = \(\frac{9 V^{2}}{\pi^{2} r^{4}}\) ……………..(i)
And S = πrl
⇒ S = πr \(\sqrt{r^{2}+h^{2}}\) (∵ l = \(\sqrt{h^{2}+r^{2}}\))
⇒ S² = π² r² (r² + h²)
= π² r² (\(\frac{9 V^{2}}{\pi^{2} r^{4}}\) + r²) [Using Eq. (i)]

⇒ S² = \(\frac{9 V^{2}}{r^{2}}\) + π² r⁴ …………(ii)

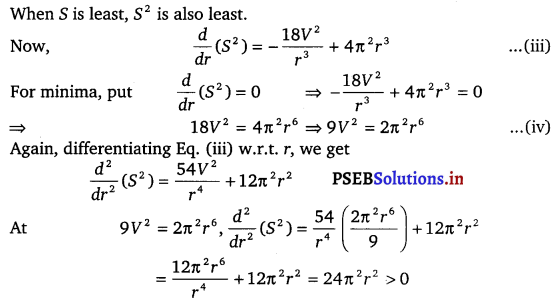
Hence, S² and therefore S is minimum when 9V² = 2π²r⁶
On putting 9 V² = 2π²r⁶ in Eq. (i) we get
2π²r⁶ = π²r⁴h²
⇒ 2r² = h²
⇒ h = √2r
Hence, altitude of right circular cone is √2 times the radius of the base.

Question 25.
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is tan^-1 √2.
Solution.

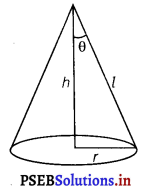
Let θ be the semi-vertical angle of the cone.
It is clear that θ ∈ [0, \(\frac{\pi}{2}\)]
Let r, h and l be the radius, height and the slant height of the cone, respectively.
The slant height of the cone is given as constant.
Now, r = l sin θ and h = l cos θ
The volume (V) of the cone is given by V = \(\frac{1}{3}\) πr² h
⇒ \(\frac{1}{3}\) π (l² sin² θ) (l cos θ)
= \(\frac{1}{3}\) π l² sin² θ cos θ
On differentiating w.r.t. θ, we get
∴ \(\frac{d V}{d \theta}\) = \(\frac{l^{2} \pi}{3}\) [sin² θ (- sin θ) + cos θ (2 sin θ cos θ)]

= \(\frac{l^{3} \pi}{3}[\) [- sin³ θ + 2sin θ cos² θ]

Again, differentiating w.r.t. θ, we get
\(\frac{d^{2} V}{d \theta^{2}}\) = \(\frac{l^{3} \pi}{3}\) [- 3 sin² θ cos θ + 2 cos³ θ – 4 sin² θ cos θ]

= \(\frac{l^{3} \pi}{3}\) [2 cos³ θ – 7 sin² θ cos θ]
For maxima put \(\frac{d V}{d \theta}\) = 0
⇒ sin³ θ = 2 sin θ cos θ v d0
⇒ tan² θ = 2
⇒ tan θ = √2
⇒ θ = tan^-1 √2
Now, when θ = tan^-1 √2, then tan² θ = 2 or sin² θ = 2 cos² θ
Then, we have

\(\frac{d^{2} V}{d \theta^{2}}\) = \(\frac{l^{3} \pi}{3}\) [2 cos³ θ – 14 cos³ θ]
= – 4πl³ cos³ θ < 0 for θ ∈ [0, \(\frac{\pi}{2}\)]

∴ By second derivative test, the volume (V) is the maximum when θ = tan^-1 √2.
Hence, for a given slant height, the semi-vertical angle of the cone of the maximum volume is tan^-1 √2.

Question 26.
Show that the semi-vertical angle of right circular cone of given surface area and maximum volume is sin^-1 (\(\frac{1}{3}\)).
Solution.
With usual notation, given that total surface area S = πrl + πr²

Direction (27 – 29): Choose the correct answer.

Question27.
The point on the curve x² = 2y which is nearest to the point (0, 5) is
(A) (2√2, 4)
(B) (2√2, 0)
(C) (0, 0)
(D) (2, 2)
Solution.
Let d be the distance of the point (x, y) on x² = 2y from the point (0, 5),
then
d = \(\sqrt{(x-0)^{2}+(y-5)^{2}}=\sqrt{x^{2}+(y-5)^{2}}\) ……………(i)

= \(\sqrt{2 y+(y-5)^{2}}\) [Putting x² = 2y]

= \(\sqrt{y^{2}-8 y+25}\)

= \(\sqrt{y^{2}-8 y+4^{2}+9}=\sqrt{(y-4)^{2}+9}\)

d is least when (y – 4)² = 0 i.e., when y = 4
when y = 4 then x² = 2 × 4
⇒ x = ± √8 = ± 2√2
∴ The points (2√2, 4) and (- 2√2, 4) on the given curve are nearest to the point (0, 5).
The correct answer is (A).

Question 28.
For all real values of x, the minimum value of \(\frac{1-x+x^{2}}{1+x+x^{2}}\) is
(A) 0
(B) 1
(C) 3
(D) \(\frac{1}{3}\)
Solution.

The correct answer is (D).

Question 29.
The maximum value of [x (x – 1) + 1]^{\(\frac{1}{3}\)},0 < x < 1 is
(A) \(\left(\frac{1}{3}\right)^{\frac{1}{3}}\)

(B) \(\frac{1}{2}\)

(C) 1
(D) 0
Solution.
Let f(x) = [x (x – 1) + 1]^{\(\frac{1}{3}\)}

∴ f'(x) = \(\frac{2 x-1}{3[x(x-1)+1]^{\frac{2}{3}}}\)

Now, f'(x) = 0
⇒ x = \(\frac{1}{2}\)
Then, we evaluate the value of f at critical point x = \(\frac{1}{2}\) and at the point of the interval [0, 1]
{i.e., at x = 0 and x = 1}.
f(0) = [0 (0 – 1) + 1]^{\(\frac{1}{3}\)} = 1;

f(1) = [1 (1 – 1) + 1]^{\(\frac{1}{3}\)} = 1

f(\(\frac{1}{2}\)) = \(\left[\frac{1}{2}\left(\frac{-1}{2}\right)+1\right]^{\frac{1}{3}}=\left(\frac{3}{4}\right)^{\frac{1}{3}}\)

Hence, we can conclude that the maximum value off in the interval [0, 1] is 1.
The correct answer is (C).

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 14 Environmental Chemistry Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 14 Environmental Chemistry

PSEB 11th Class Chemistry Guide Environmental Chemistry InText Questions and Answers

Question 1.
Define environmental chemistry.
Answer:
Environmental chemistry is the study of chemical and biochemical processes occurring in nature. It deals with the study of origin, transport, reaction, effects, and fates of various chemical species in the environment.

Question 2.
Explain tropospheric pollution in 100 words.
Answer:
Tropospheric pollution occurs due to the presence of undesirable solid or gaseous particles in the air. The major gaseous and particulate pollutants present in the troposphere are :
(i) Gaseous air pollutants : These are oxides of sulphur, nitrogen and carbon, hydrogen sulphide, hydrocarbons, ozone and other oxidants.
(ii) Particulate pollutants : These are dust, mist, fumes, smoke, smog, etc.

Gaseous Air Pollutants
(a) Oxides of sulphur : These are produced when sulphur containing fossil fuel is burnt. S02 gas is poisonous to both animals and plants.
(b) Oxides of nitrogen : These are produced by the reaction of nitrogen and oxygen at high altitudes when lightning strikes.

(c) Hydrocarbons : Incomplete combustion of fuel used in automobiles is the major source for the release of hydrocarbon. These are carcinogenic and cause cancer. They also harm plants.
(d) Oxides of carbon : Carbon monoxide is one of the most serious air pollutants. It is highly poisonous to living beings because it blocks the supplyof oxygen to the organs and tissues. It is produced due to the incomplete combustion of carbon.
Carbon dioxide is the main contributor towards green house effect and global warming. It is released into the atmosphere by respiration, burning of fossil fuels and by decomposition of limestone during cement manufacturing.

Question 3.
Carbon monoxide gas is more dangerous than carbon dioxide gas. Why?
Answer:
Carbon dioxide (CO₂) and carbon monoxide (CO) gases are emitted during the combustion of various fuels. Carbon monoxide is poisonous, whereas carbon dioxide is non-toxic in nature.
Carbon monoxide is poisonous because it is capable of forming a complex with haemoglobin (carboxyhaemoglobin), which is more stable than the
oxygen-heamoglobin complex. The concentration range (3-4% )of carboxyhaemoglobin decreases the oxygen-carrying capacity of blood. This results in headaches, weak eyesight, nervousness, and cardiovascular disorders. A more increased concentration may even lead to death.
Carbon dioxide is not poisonous. It proves harmful only at very high concentrations.

Question 4.
List gases which are responsible for greenhouse effect.
Answer:
The major greenhouse gases are:
1. Carbon dioxide (CO₂)
2. Methane (CH₄)
3. Nitrous oxide (NO)
4. Ozone (O₃)
5. Chlorofluorocarbons (CFCs)

Question 5.
Statues and monuments in India are affected by acid rain. How?
Answer:
Acid rain is a byproduct of various human activities that leads to the emission of oxides of sulphur and nitrogen in the atmosphere. These oxides undergo oxidation and then react with water vapour to form acids.
2SO₂(g) + O₂(g) + 2H₂O(l) > 2H₂SO₄(aq)
4NO₂(g) + O₂(g) + 2H₂O(l) > 4HNO₃(aq)
Acid rain causes damage to buildings and structures made of stone and metal.
In India, limestone is a major stone used in the construction of various monuments and statues, including the Taj Mahal.
Acid rain reacts with limestone as:
CaCO₃ + H₂SO₄ > CaSO₄ + H₂O + CO₂
This results in the loss of lustre and colour of monuments, leading to their disfiguration.

Question 6.
What is smog? How is classical smog different from photochemical smog?
Answer:
Smog is a kind of air pollution. It is the blend of smoke and fog. There are two kinds of smog.
(a) Classical smog
(b) Photochemical smog ^
The two smogs can be differentiated as follows :
table

Question 7.
Write down the reactions involved during the formation of photochemical smog.
Answer:
Photochemical smog is formed as a result of the reaction of sunlight with hydrocarbons and nitrogen oxides. Ozone, nitric oxide, acrolein, formaldehyde, and peroxyacetyl nitrate (PAN) are common components of photochemical smog. The formation of photochemical smog can be summarized as follows:

Burning of fossil fuels leads to the emission of hydrocarbons and nitrogen dioxide in the atmosphere. High concentrations of these pollutants in air results in their interaction with sunlight as follows:

Question 8.
What are the harmful effects of photochemical smog and how can they be controlled?
Answer:
Effects of photochemical smog : Photochemical smog is oxidizing smog owing to the presence of N02 and 03 causing corrosion of metals, stones, rubber, and painted surfaces. The other major components of photochemical smog are PAN, acrolein, and formaldehyde. Both PAN and ozone are eye irritants, while nitric oxide (formed from NO₂) causes nose and throat irritation. At higher concentrations, photochemical smog causes chest pain, headaches, throat dryness, and various respiratory ailments.
Control measures : Photochemical smog results from the burning of fossil fuels and automobile fuels that emit NO₂ and hydrocarbons, which in turn form ozone, PAN and other chemicals. The use of catalytic converters in automobiles is recommended to prevent the release of NO₂ and hydrocarbons into the atmosphere.
Plantation of plants such as Finns, Juniparus, Quercus, Pyrus, and Vitis is also advised as these plants have the capability to metabolize NO₂.

Question 9.
What are the reactions involved for ozone layer depletion in the stratosphere?
Answer:
In the stratosphere, ozone is a product of the action of UV radiations on dioxygen as:

Reaction (ii) indicates the dynamic equilibrium existing between the production and decomposition of ozone molecules. Any factor that disturbs the equilibrium may cause depletion of ozone layer by its decomposition. One such factor is the release of chlorofluorocarbon compounds (CFCs). These are non-reactive, non-flammable molecules that are used in refrigerators, air conditioners, plastics, and electronic industries.
Once released CFCs mix with atmospheric gases and reach the stratosphere, where they are decomposed by UV radiations.

The chlorine free radical produced in reaction (iii) reacts with ozone as:

The radicals further react with atomic oxygen to produce more chlorine radicals as:

The regeneration of causes a continuous breakdown of ozone present in the stratosphere damaging the ozone layer.

Question 10.
What do you mean by ozone hole? What are its consequences? Ans. In Polar regions, stratospheric clouds provide the surface for chlorine nitrate and hypochlorous acid, which react further to give molecular chlorine. Molecular chlorine and H0C1 are photolysed to give chlorine-free radicals.

Hence, a chain reaction is initiated. The chlorine-free radical is continuously regenerated, thereby depleting the ozone layer. This phenomenon is known as the ozone hole.

Effects of depletion of ozone layer : The ozone layer protects the Earth from the harmful UV radiations of the sun. With the depletion of the layer, more radiation will enter the Earth’s atmosphere. UV radiations are harmful because they lead to the ageing of skin, cataract, skin cancer, and sunburns. They cause death of many phytoplanktons, which leads to a decrease in fish productivity. Excess exposure may even causes mutation in plants.
Increase in UV radiations, decreases the moisture content of the soil and damages both plants and fibres.

Question 11.
What are the major causes of water pollution? Explain.
Answer:
Several human activities caused water population which leads to the presence of several undesirable substances in water.
Major water pollutants with their sources have been tabulated as follows:
table

Roles played by major pollutants are :
1. Pathogens : These water pollutants include bacteria and other organisms. They enter water from animal excreta and domestic sewage. Bacteria present in human excreta (for example, Escherichia coli and Streptococcus faecalis) cause gastrointestinal diseases.
2. Organic wastes : These are biodegradable wastes that pollute water as a result of run off. The presence of excess organic wastes in water decreases the amount of oxygen held by water. This decrease in the amount of dissolved oxygen inhibits aquatic life.
3. Chemical pollutants : These are water soluble chemicals like heavy metals such as cadmium, mercury, nickel, etc. The presence of these chemicals (above the tolerance limit) can damage the kidneys, central nervous system, and liver.

Question 12.
Have you ever observed any water pollution in your area? What measures would you suggest to control it?
Answer:
Water pollution arises as a result of various human activities. This includes discharges from waste water treatment plants, run-off from agricultural fields, storm water drainage, etc. Pollutants from these sources enter the water bodies, thereby contaminating the water and rendering it impure.
Industries and chemical factories discharge toxic, heavy metals such as Fe, Mn, Al, etc., along with organic wastes into water. Domestic sewage and animal excreta are also responsible for pathogenic contamination of water.
These pollutants make water unfit for drinking.
Therefore, all industrial and chemical discharges should be made free from toxic metals before allowing them to enter a water body. The concentration of these pollutants should be checked regularly. Compost should be preferred over chemical fertilizers in gardens and agricultural fields to avoid harmful chemicals from entering ground water.

Question 13.
What do you mean by Biochemical Oxygen Demand (BOD)?
Answer:
Biochemical oxygen demand is the amount of oxygen required by bacteria to decompose organic matter in a certain volume of sample of water. Clean water would have a BOD value of less than 5 ppm, whereas highly polluted water has a BOD value of 17 ppm or more.

Question 14.
Do you observe any soil pollution in your neighbourhood? What efforts will you make for controlling the soil pollution?
Answer:
Major sources of soil pollution are industrial wastes and agricultural pollutants such as pesticides, fertilizers, etc.
It is very important to maintain the quality and fertility of soil to ensure and sustain the growth of plants and food crops.
Insecticides like DDT are not soluble in water. For this reason, they remain in soil for a long time contaminating the root crops. Pesticides like Aldrin and Dieldrin are non-biodegradable and highly toxic in nature. They can enter the higher trophic levels through food chains, causing metabolic and physiological disorders. The same is true for industrial wastes that comprises of several toxic metals like Pb, As, Hg, Cd, etc.
Hence, the best way to check soil pollution is to avoid direct addition of pollutants to the soil. Also, wastes should undergo proper treatment. They should be recycled and only then, allowed to be dumped. i

Question 15.
What are pesticides and herbicides? Explain giving examples.
Answer:
Pesticides are a mixture of two or more substances. They are used for killing pests. Pests include insects, plant pathogens, weeds, molluscs, etc., that destroy the plant crop and spread diseases. Aldrin and dieldrin are the names of some common pesticides.
Herbicides are pesticides specially meant for killing weeds. For example, sodium chlorate (NaClO₃), sodium arsenite (Na₃AsO₃) etc.

Question 16.
What do you mean by green chemistry? How will it help in reducing environmental pollution?
Answer:
Green chemistry is a production process that aims at using the existing knowledge and principles of chemistry for developing and implementing chemical products and processes to reduce the use and generation of substances hazardous to the environment.
The release of different harmful chemicals (particulates, gases, organic and inorganic wastes) causes environmental pollution. In green chemistry, the reactants to be used in chemical reactions are chosen in such a way that the yield of the end products is up to 100%. This prevents or limits chemical pollutants from being introduced into the environment. Through the efforts of green chemists, H₂O₂ has replaced tetrachloroethane and chlorine gas in drying and bleaching of paper.

Question 17.
What would have happened if the greenhouse gases were totally missing in the earth’s atmosphere? Discuss.
Answer:
Earth’s most abundant greenhouse gases are CO₂, CH₄, O₃ , CFCs and water vapour. These gases are present near the Earth’s surface. They absorb solar energy that is radiated back from the surface of the Earth. The absorption of radiation results in the heating up of the atmosphere. Hence, greenhouse gases are essential for maintaining the temperature of the Earth for the sustenance of life.
In the absence of greenhouse gases, the average temperature of the Earth will decrease drastically, making it uninhabitable. As a result, life on Earth would be impossible.

Question 18.
A large number of fish are suddenly floating dead on a lake. There is no evidence of toxic dumping but you find an abundance of phytoplankton. Suggest a reason for the fish kill.
Answer:
The amount of dissolved oxygen present in water is limited. The abundance of phytoplanktons causes depletion of this dissolved oxygen. This is because phytoplanktons are degraded by bacteria present in water. For their decomposition they require a large amount of oxygen. Hence, they consume the oxygen dissolved in water. As a result, the BOD level of water drops below 6 ppm, inhibiting the growth of fish and causing excessive fish kill.

Question 19.
How can domestic waste be used as manure?
Answer:
Depending upon the nature of the waste, domestic waste can be segregated into two categories i.e., biodegradable and non-biodegradable. Biodegradable waste such as leaves, rotten food, etc. should be deposited in land fills, where they get decomposed aerobically and anaerobically into manure. Non-biodegradable waste (which cannot be degraded) such as plastic, glass, metal scraps etc. should be sent for recycling.

Question 20.
For your agricultural field or garden you have developed a compost producing pit. Discuss the process in the light of bad ’ odour, flies and recycling of wastes for a good produce.
Answer:
It is essential to take proper care of the compost producing pit in order to protect ourselves from bad odour and flies.
It should be kept covered to minimize bad odour and prevent flies from entering it.
The recyclable waste should not be dumped in the compost producing pit. It should be sent to the industries through vendors for recycling.

Punjab State Board Syllabus PSEB 11th Class Hindi Book Solutions Guide Pdf is part of PSEB Solutions for Class 11.

PSEB 11th Class Hindi Guide | Hindi Guide for Class 11 PSEB

Hindi Guide for Class 11 PSEB | PSEB 11th Class Hindi Book Solutions

प्राचीन काव्य

• Chapter 1 साखी
• Chapter 2 रामराज्य वर्णन
• Chapter 3 सवैये
• Chapter 4 दोहे
• Chapter 5 पदावली

आधुनिक काव्य

• Chapter 6 पवनदूत
• Chapter 7 वह तोड़ती पत्थर, जागो फिर एक बार
• Chapter 8 वीरों का कैसा हो वसन्त?, ठुकरा दो या प्यार करो
• Chapter 9 मानव
• Chapter 10 ऐ वीरो, भारतवर्ष के
• Chapter 11 कहाँ तो तय था
• Chapter 12 वारिसनामा-स्वराज के लिए बहे लहू
• Chapter 13 बुद्धम शरणम् गच्छामि
• Chapter 14 पिघलती साँकलें, तुम-हम

निबन्ध भाग

• Chapter 15 भारत की सांस्कृतिक एकता
• Chapter 16 युवाओं से
• Chapter 17 स्त्री के अर्थ-स्वातंत्र्य का प्रश्न
• Chapter 18 भीड़ में खोया आदमी
• Chapter 19 रसायन और हमारा पर्यावरण
• Chapter 20 एक मिलियन डालर दृश्य
• Chapter 21 शहीद सुखदेव
• Chapter 22 विज्ञापन युग

कहानी भाग

• Chapter 23 प्रेरणा
• Chapter 24 उसकी माँ
• Chapter 25 सेब और देव
• Chapter 26 मजबूरी

लघु कथाएँ

• Chapter 27 अपना-अपना दःख
• Chapter 28 अटूट बंधन
• Chapter 29 हरियाली
• Chapter 30 जन्मदिन
• Chapter 31 रिश्ते
• Chapter 32 नई नौकरी

एकांकी भाग

• Chapter 33 अधिकार का रक्षक
• Chapter 34 टूटते परिवेश

PSEB 11th Class Hindi Book हिन्दी साहित्य का इतिहास

• आदिकाल
• भक्तिकाल

PSEB 11th Class Hindi Book व्यावहारिक व्याकरण

• सन्धि और सन्धिच्छेद
• वाक्य विचार : वाक्य विश्लेषण/संश्लेषण
• रस : शृंगार, हास्य, करुण, शांत, वीर, रौद्र, भयानक, वीभत्स, अद्भुत

PSEB 11th Class Hindi Book रचनात्मक लेखन

• पत्र-लेखन
• अनुच्छेद-लेखन

PSEB 11th Class Hindi Book संप्रेषण कौशल

• पंजाबी वाक्यों का हिन्दी में अनुवाद
• पारिभाषिक शब्दावली (A से I तक)
• संक्षेपिका लेखन / संक्षेपीकरण

Syllabus of Class 11 PSEB Hindi 2021-22

पाठ्यकम (2021 – 22)
विषय : हिंदी
कक्षा : ग्यारहवीं

समय :3 घंटे

शवकिं = 80
आंतरिक मूल्यांकन = 20

विषय वस्तु

भाग – क : अति लघूत्तर प्रश्न (वस्तुनिष्ठ प्रश्न)
संधि : स्वर, विसर्ग तथा व्यंजन
वाक्य विश्लेषण, वाक्य संश्लेषण
पाठ्य-पुस्तक
हिंदी साहित्य का इतिहास (आदिकाल एवं भक्तिकाल)
रस

भाग-ख : पाठ्य-पुस्तक (हिंदी पुस्तक – 11)

भाग-ग : हिंदी साहित्य का इतिहास (आदिकाल एवं भक्तिकाल)

भाग-घ : रचनात्मक लेखन
1. पत्र-लेखन
2. अनुच्छेद लेखन

भाग-ङ : व्यावहारिक ज्ञान
1. पंजाबी वाक्यों का हिंदी अनुवाद
2. पारिभाषिक शब्दावली (A से लेकर I तक)
3. संक्षेपीकरण

भाग-च : रस (शृंगार,करुण,हास्य, शांत, रौद्र ,वीर,अद्भुत,भयानक और वीभत्स)

पंजाब स्कूल शिक्षा बोर्ड द्वारा निर्धारित पाठ्य-पुस्तकें

• हिंदी पुस्तक – 11
• हिंदी भाषा बोध और व्याकरण (ग्यारहवीं और बारहवीं कक्षा के लिए)
• हिंदी साहित्य का इतिहास (ग्यारहवीं और बारहवीं कक्षा के लिए)

Punjab State Board Syllabus Class 11 General English Guide PSEB Pdf, A Panorama of Life PSEB Solutions Class 11, PSEB 11th Class English Book Solutions Guide Pdf download is part of PSEB Solutions for Class 11.

A Panorama of Life PSEB Guide Pdf | Class 11 General English Guide PSEB Pdf

English Guide for Class 11 PSEB Pdf Download | A Panorama of Life Book Pdf

A Panorama of Life PSEB Solutions Class 11

A Panorama of Life Book Pdf Prose

• Chapter 1 Gender Bias
• Chapter 2 The Portrait of a Lady
• Chapter 3 Of Studies
• Chapter 4 Liberty and Discipline
• Chapter 5 A President Speaks
• Chapter 6 The Earth is not Ours
• Chapter 7 Let’s Not Forget the Martyrs
• Chapter 8 Water- A True Elixir
• Chapter 9 The First Atom Bomb
• Chapter 10 No Time for Fear

A Panorama of Life PSEB Guide Pdf Poetry

• Poem 1 Lines Written in Early Spring
• Poem 2 Mother’s Day
• Poem 3 Television
• Poem 4 Upagupta
• Poem 5 Confessions of a Born Spectator
• Poem 6 The Little Black Boy
• Poem 7 A Thing of Beauty is a Joy for Ever

Class 11 General English Guide PSEB Pdf Supplementary Reading

• Chapter 1 An Astrologer’s Day
• Chapter 2 The Tiger in the Tunnel
• Chapter 3 Sparrows
• Chapter 4 The Model Millionaire
• Chapter 5 The Panch Parmeshwar
• Chapter 6 The Peasant’s Bread

PSEB 11th Class English Grammar & Composition

• Reading Comprehension Unseen Passages

PSEB 11th Class English Grammar

• Prepositions
• Determiners
• Modals
• Tenses
• Transformation of Sentences & Removal and Use of ‘Too’
• Active and Passive Voice
• Narration / Direct and Indirect Speech
• Use of Words as Different Parts of Speech
• Translation

PSEB 11th Class English Composition

• Notice Writing
• Message Writing
• Advertisement Writing
• Letter Writing
• Note-Making

PSEB Class 11 English Syllabus

Class – XI
General English

Time: 3hrs

Theory: 80 Marks
IA: 20 Marks
(Listening and Speaking skills-based practical: 18 marks and Book bank: 2 marks)
Total: 100 Marks

Syllabus

Section A

Reading Skills

Two Comprehension unseen passages

Section B

Writing Skills, Grammar & Translation

• Preposition
• Determiners
• Use of the same word as noun, verb, and adjective
• Modals
• Tenses
• Removal and use of too
• Voice
• Narration

Composition

• Note Making
• Message Writing
• Notice Writing
• Advertisement Writing
• Letter Writing (only social and personal)

Section C
(Literature Text Books)

Lessons for Intensive Study

1. Gender Bias
2. The Portrait of a Lady
3. Liberty and Discipline
4. A President Speaks
5. The Earth is not Ours
6. Let’s Not Forget the Martyrs
7. Water- A True Elixir
8. No Time for Fear

Poetry

1. Lines Written in Early Spring
2. Mother’s Day
3. Upagupta
4. Confessions of A Born Spectator
5. The Little Black Boy
6. A Thing of Beauty is a Joy For Ever

Lessons for Extensive Study

1. An Astrologer’s Day
2. The Tiger in the Tunnel
3. Sparrows
4. The Model Millionaire
5. The Panch Parmeshwar
6. The Peasant’s Bread

The books were prescribed & published by the Punjab School Education Board.

• (General English XI) A Panorama of Life
• English Grammar and Composition for XI and XII

Translation from English to Hindi/Punjabi and Translation from Hindi/ Punjabi to English.

From Chapter 18 The Art of Translation given in the book English Grammar And Composition for XI and XII

Note: Following two lessons & one poem has been deleted from the syllabus from the academic session 2020-21 onwards.

• Of Studies
• The First Atom Bomb
• Television

Punjab State Board PSEB 11th Class Chemistry Important Questions Chapter 13 Hydrocarbons Important Questions and Answers.

PSEB 11th Class Chemistry Important Questions Chapter 13 Hydrocarbons

Very Short Answer Type Questions

Question 1.
Why do hydrocarbon molecules with an odd number of carbon atoms have lower melting points than those with an even number of carbon atoms?
Answer:
Molecules with odd number of carbon atoms have lower melting points because they do not fit into crystal lattice easily whereas, hydrocarbons with even number of carbon atoms can fit into crystal lattice easily.

Question 2.
Why do the C—C bonds rather than C—H bonds break during cracking of alkanes?
Since, the bond dissociation energy of C—C bonds (348 kJ mol^-1) is lower than bond dissociation energy of C—H bonds (414 kJ mol^-1), therefore, during cracking of alkanes, C—C bonds break more easily than C—H bonds.

Question 3.
Which of the two frans-but-2-ene or trans-2-ene is non-polar?
Answer:
In frans-but-2-ene, the dipole moments of the two C—CH₃ bonds are equal and opposite and therefore, they cancel out each other. Hence, trans-2-butene is non-polar.

Question 4.
Explain why alkynes are less reactive than alkenes toward addition of Br₂.
Answer:
The three-membered ring bromonium ion formed from the alkyne (A) has a full double bond causing it to be more strained and less stable than the one from the alkene (B),

Also, the carbon’s of (A) that are part of the bromonium ion have more s-character than (B), further making (A) less stable than (B).

Question 5.
Explain the reason for extra ordinary stability of benzene in spite of presence of three double bonds in it.
Answer:
It is due to resonance, 6 π-electrons are delocalised.

Question 6.
How will you demonstrate that double bonds of benzene are somewhat different from that of olefines?
Answer:
The double bonds of olefines decolourise Br₂ in CCl₄ and discharge the pink colour of Baeyer’s reagent with simultaneous formation of a brown ppt. of MnO₂ while those of benzene do not.

Question 7.
n-propylmagnesium bromide on hydrolysis gives propane. Is there any other Grignard reagent which also gives propane? If so, give its name, structure and equation for the reaction.
Answer:
Iso-propylmagnesium bromide, (CH₃)₂CHMgBr,
(CH₃)₂CHMgBr + H₂O → CH₃CH₂CH₃ + Mg(OH)Br

Question 8.
How would you distinguish between
(i) But-l-yne and but-2-yne
(ii) Propene and propyne
Answer:
(i) Upon treatment with ammoniacal solution of AgNO₃, but-l-yne would give white ppt. whereas but-2-yne does not react.
(ii) Upon treatment with ammoniacal solution of AgNO₃, propyne would give white ppt. whereas propene does not react.

Question 9.
Give the structure of the alkene (C₄H₈) which adds on HBr in the presence and in absence of peroxide to give the same product, C₄H₉Br.
Answer:

Question 10.
Convert 1-bromopropane to 2-bromopropane.
Answer:

Short Answer Type Questions

Question 1.
Write hydrocarbon radicals that can be formed as intermediates during monochlorination of 2-methylpropane. Which of them is more stable? Give reasons.
Answer:
2-methylpropane gives two types of radicals

Radical (I) is more stable because it is 3° and stabilised by nine hyperconjugative structures (as it has 9 a-hydrogens). Radical (II) is less stable because it is 1° and stabilised by only one hyperconjugative structure (as it has only 1 a-hydrogen).

Question 2.
Rotation around carbon-carbon single bond of ethane is not completely free. Justify the statement.
Answer:
Rotation around C—C single bond is not completely free and it is restricted due to repulsions between the electron clouds of C—H bonds in the adjacent carbon atoms. Therefore, ethane exists in infinite number of conformations. Out of these, two extreme conformations are staggered and eclipsed.

Question 3.
List the following alkenes in decreasing order of reactivity towards electrophilic addition. ‘
(i) ClCH₂CH = CH₂ (ii) (CH₃)₂C = CH₂ (iii) CH₃CH = CH₂ (iv) CH₂ = CHCl
Explain your order.
Answer:
Electron donating alkyl groups make the rt-bond more electron rich and more reactive. Conversely, electron withdrawing groups such as Cl make the rc-bond more electron deficient and less reactive. The order is

Question 4.
The intermediate carbocation formed in the reactions of HI, HBr and HCl with propene is the same and the bond energy of HC1, HBr and HI is 430.5 kJ mol^-1, 363.7 kJ mol1 and 296.8 kJ mol^-1 respectively. What will be the order of reactivity of these halogen acids?
Answer:
Addition of halogen acids to an alkene is an electrophilic addition reaction.

First step is slow so, it is rate determining step. The rate of this step depends on the availability of proton. This in turn depends upon the bond dissociation enthalpy of the H—X molecule. Lower the bond dissociation enthalpy of H—X molecule, greater the reactivity of halogen halide. Since, the bond dissociation energy decreases in the order; HI (296.8 kJ mol^-1) < HBr (363.7 kJ mol^-1) < HCl (430.5 kJ mol^-1)
Therefore the reactivity of the halogen acids decreases from HI to HCl i.e., HI > HBr > HCl.

Question 5.
An alkyl halide (X) of formula C₆H₁₃Cl on treatment with alcoholic KOH or potassium terf-butoxide gives two isometric alkenes Y and Z(C₆H₁₂). Both alkenes on hydrogenation give 2, 3-dimethylbutane. Predict the structure of X, Y and Z.
Answer:

Long Answer Type Questions

Question 1.
Assign structures to the following:
(i) An alkyne (X) has molecular formula CsHg. It reacts neither with sodamide nor with ammoniacal cuprous chloride.
(ii) A hydrocarbon ‘Y’ decolourises bromine water. On ozonolysis it gives 3-methyl butanal and formaldehyde. Give the name of the compound.
(iii) A hydrocarbon (Z) has molecular formula C8H10. It does not decolourise bromine water and is oxidised to benzoic acid on heating with K₂Cr₂O₇. It can also have three other isomers A, B and C. Write the structures of Z, A, B and C.
Ans. (i) Alkyne X is CsHg. Since, it does not react with sodamide or ammoniacal, cuprous chloride, the triple bond cannot be terminal. ∴ X is CH₃CH₂C = CCH₃ (Pent-2-yne)
(ii) Hydrocarbon ‘Y’ is alkene because it decolourises bromine water. From the products of ozonolysis, the structure of alkene can be predicted.

(iii) Since, it does not decolourise bromine water, it is arene. Its formula is

Question 2.
(i) Arrange the three isomeric pentanes in order of increasing stability at room temperature.
(ii) Give a method of preparation of propane from (a) an alkene (b) an alkyl halide.
(iii) Write the structure of all the alkenes that can be hydrogenated to form 2-methyl butane.
(iv) Why is light or heat necessary to initiate the chlorination reaction?
Answer:
(i) The stability of structural isomers generally increases with increasing branching. Thus,
Pentane, [CH₃(CH₂)₃CH₃] iso-pentane, [(CH₃)₂CHCH₂CH₃] < neo-pentane, [(CH₃)₄C]

(iii) The alkenes must have the same carbon skeleton as 2-methyl butane.

There are three different positions for the double bond; hence the three different alkenes are :

(iv) The Cl—Cl bond must be broken to form Cl radical before the reaction with methane. This homolysis requires energy, which is supplied either by heat or light.

Punjab State Board Syllabus A Rainbow of English 12 Class PSEB Solutions Pdf, General English Class 12 PSEB Solutions, English Guide for Class 12 PSEB Pdf Free Download is part of PSEB Solutions for Class 12.

A Rainbow of English 12 Class Solutions PSEB | General English Class 12 PSEB Solutions

English Guide for Class 12 PSEB Pdf Free Download | General English Class 12 PSEB Book

A Rainbow of English 12 Class PSEB Solutions Pdf

A Rainbow of English 12 Class Guide Prose

• Chapter 1 Hassan’s Attendance Problem
• Chapter 2 The March King
• Chapter 3 Thinking Out of the Box: Lateral Thinking
• Chapter 4 Robots and People
• Chapter 5 On Giving Advice
• Chapter 6 On Saying “Please”
• Chapter 7 The Story of My Life
• Chapter 8 Two Gentlemen of Verona
• Chapter 9 In Celebration of Being Alive
• Chapter 10 Ghadari Babas in Kalapani Jail

A Rainbow of English 12 Class Solutions PSEB Poetry

• Poem 1 Prayer of the Woods
• Poem 2 On Friendship
• Poem 3 The Echoing Green
• Poem 4 Once upon a Time
• Poem 5 Cheerfulness Taught By Reason
• Poem 6 Father Returning Home
• Poem 7 The Road Not Taken
• Poem 8 On His Blindness

General English Class 12 PSEB Solutions Supplementary Reading

• Chapter 1 The School for Sympathy
• Chapter 2 A Chameleon
• Chapter 3 Bholi
• Chapter 4 The Gold Frame
• Chapter 5 The Barber’s Trade Union
• Chapter 6 The Bull beneath the Earth

PSEB 12th Class English Grammar & Composition

• Reading Comprehension Unseen Passages Type-I
• Reading Comprehension Unseen Passages Type-II

PSEB 12th Class English Grammar

• Determiners
• Use of Non-finites (Infinitives, Gerunds and Participles)
• Transformation of Sentences (Simple, Compound & Complex)
• Active and Passive Voice
• Narration / Direct and Indirect Speech
• Translation

PSEB 12th Class English Composition

• Precis Writing
• Application Writing
• Letter Writing Letters to Editor
• Letter Writing Business Letters
• E-Mail Writing
• Explaining Newspaper Headlines

General English Class 12 PSEB Syllabus

Class – XII
General English
(2021-22)

Time: 3hrs

Theory: 80 Marks
IA: 20 Marks
(Listening and Speaking skills-based practical: 18 marks and Book bank: 2 marks)
Total: 100 Marks

Syllabus

Unseen Passages For Testing Reading Skills
Text Book

Section A (Lessons for Intensive Study)

1. Hassan’s Attendance Problem – Sudha Murthy
2. The March King – Katherine Little Bakeless
3. Thinking Out of the Box: Lateral Thinking – Adapted from the article from the Internet
4. On Saying ‘Please’ – A. G. Gardiner
5. The Story of My Life – Helen Keller
6. Two Gentlemen of Verona – A. J. Cronin
7. In Celebration of Being Alive – Dr. Christian Barnard
8. Gadari Babas in Kalapani Jail – Dr. Harish Puri

Section B (Poetry)

1. Prayer of the Woods – Anonymous
2. On Friendship – Khalil Gibran
3. The Echoing Green – William Blake
4. Once upon a Time – Gabriel Okara
5. Father Returning home – Dilip Chitre
6. The Road Not Taken – Robert Frost
7. On His Blindness – John Milton

Section C (Lessons for Extensive Study)

1. The School for Sympathy – E. V. Lucas
2. A Chamelon – Anton Chekhov
3. Bholi – K.A. Abbas
4. The Gold Frame – R.K. Luxman
5. The Barber’s Trade Union – Mulk Raj Anand
6. The Bull beneath the Earth – K.S. Virk

Grammar, Composition & Translation

Grammar

1. Determiners
2. Use of Non-finites (Infinitives, Gerunds, Participles)
3. Transformation of Sentences
4. Voice
5. Narration

Composition

1. Precis writing
2. Letter writing (Official/Business/To Editors)
3. Applications
4. Explaining Newspaper Headlines
5. E-Mail writing

Translation from English to Hindi/Punjabi and Translation from Hindi/ Punjabi to English.

From Chapter 18 The Art of Translation given in the book English Grammar And Composition for XI and XII

Note: Following two lessons & one poem has been deleted from the syllabus from the academic session 2020-21 onwards.

• Robots and People – Isaac Asimov
• On Giving Advice – Joseph Addison
• Cheerfulness Taught by Reason – Elizabeth Barret Browning

Punjab State Board PSEB 11th Class Physical Education Book Solutions Chapter 4 ਯੋਗ Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 11 Physical Education Chapter 4 ਯੋਗ

Physical Education Guide for Class 11 PSEB ਯੋਗ Textbook Questions and Answers

ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਆਸਣ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ ? (How many types of Asanas are there ?)
ਉੱਤਰ-
ਆਸਣ ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ-

1. ਧਿਆਨਾਤਮਿਕ ਆਸਣ (Meditative Asanas)
2. ਆਰਾਮਦਾਇਕ ਆਸਣ (Relaxative Asanas)

ਪ੍ਰਸ਼ਨ 2.
ਯੋਗ ਦੀ ਪਰਿਭਾਸ਼ਾ, ਅਰਥ ਅਤੇ ਮਹੱਤਤਾ ਬਾਰੇ ਦੱਸੋ । (Give definition, meaning and importance of Yoga.)
ਉੱਤਰ-
ਯੋਗ ਦਾ ਅਰਥ (Meaning of Yoga)
ਭਾਰਤ ਦੇ ਵਿਦਵਾਨਾਂ ਨੇ ਆਤਮ-ਸ਼ਕਤੀ ਰਾਹੀਂ ਸੰਸਾਰ ਨੂੰ ਯੋਗ ਵਿਗਿਆਨ ਤੋਂ ਜਾਣੂ ਕਰਵਾਇਆ ਅਤੇ ਉਹਨਾਂ ਵਿਚ ਦੱਸਿਆ ਕਿ ਮਨੁੱਖ ਦਾ ਸਰੀਰ ਅਤੇ ਮਨ ਵੱਖਰੇ ਹਨ ਜੋ ਕਿ ਉਸ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਦਿਸ਼ਾ ਵੱਲ ਖਿੱਚਦੇ ਹਨ ਜਿਸ ਕਰਕੇ ਮਨੁੱਖ ਦੀਆਂ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਸ਼ਕਤੀਆਂ ਦਾ ਵਿਕਾਸ ਰੁਕ ਜਾਂਦਾ ਹੈ । ਸਰੀਰ ਅਤੇ ਮਨ ਨੂੰ ਇਕਾਗਰ ਕਰਕੇ ਪਰਮਾਤਮਾ ਨਾਲ ਇਕਮਿਕ ਹੋਣ ਦਾ ਰਸਤਾ ਦੱਸਿਆ, ਜਿਸ ਨੂੰ ਯੋਗ ਦੇ ਨਾਂ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ।

ਯੋਗ ਸੰਸਕ੍ਰਿਤ ਭਾਸ਼ਾ ਦੇ ਸ਼ਬਦ ‘ਯੁਜ’ ਤੋਂ ਬਣਿਆ ਹੈ ਜਿਸ ਦਾ ਅਰਥ ਜੋੜ ਜਾਂ ਮੇਲ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਰੀਰ ਅਤੇ ਮਨ ਦੇ ਮੇਲ ਨੂੰ ਯੋਗ ਕਹਿੰਦੇ ਹਨ | ਯੋਗ ਉਹ ਕਿਰਿਆ ਜਾਂ ਸਾਧਨ ਹੈ ਜਿਸ ਨਾਲ ਆਤਮਾ ਪਰਮਾਤਮਾ ਨਾਲ ਮਿਲਦੀ ਹੈ ।

ਇਤਿਹਾਸ (History) – ਯੋਗ ਸ਼ਬਦ ਬਹੁਤ ਸਮੇਂ ਤੋਂ ਪ੍ਰਚਲਿਤ ਹੈ। ਗੀਤਾ ਵਿਚ ਵੀ ਯੋਗ ਬਾਰੇ ਬਹੁਤ ਲਿਖਿਆ ਮਿਲਦਾ ਹੈ । ਰਮਾਇਣ ਅਤੇ ਮਹਾਂਭਾਰਤ ਯੁੱਧ ਵਿਚ ਵੀ ਇਸ ਸ਼ਬਦ ਦੀ ਬੜੀ ਵਰਤੋਂ ਹੋਈ ਹੈ । ਇਹਨਾਂ ਪਵਿੱਤਰ ਗ੍ਰੰਥਾਂ ਵਿਚ ਯੋਗ ਨਾਲ ਮੁਕਤੀ (Moksh) ਹਾਸਲ ਕਰਨ ਬਾਰੇ ਵਿਸਥਾਰ ਪੂਰਵਕ ਲਿਖਿਆ ਮਿਲਦਾ ਹੈ । ਇਹਨਾਂ ਵਿਦਵਾਨਾਂ ਵਿਚੋਂ ਪ੍ਰਸਿੱਧ ਵਿਦਵਾਨ ਪਾਤੰਜਲੀ ਹੈ ਜਿਸ ਨੇ ਯੋਗ-ਵਿਗਿਆਨ ‘ਤੇ ਲਿਖਿਆ ਪਰ ਯੋਗ ਦੇ ਅਰਥਾਂ ਵਿਚ ਸਮਾਨਤਾ ਨਹੀਂ | ਪਾਤੰਜਲੀ ਅਨੁਸਾਰ, “ਚਿੱਤ ਦੀ ਵਿਰਤੀ ਤੇ ਨਿਰੋਧ ਹੀ ਯੋਗ ਹੈ ।’

(According to Patanjali, “Yoga has been defined as the Nirodh of the virti of the citta (mind).”) ਗੀਤਾ ਵਿਚ ਭਗਵਾਨ ਕ੍ਰਿਸ਼ਨ ਨੇ ਲਿਖਿਆ ਹੈ ਕਿ ਠੀਕ ਢੰਗ ਨਾਲ ਕੰਮ ਕਰਨਾ ਹੀ ਯੋਗ ਹੈ ।

ਡਾ. ਸੰਪੂਰਨਾਨੰਦ (Dr. Sampurnanand) ਅਨੁਸਾਰ, “ਯੋਗ ਅਧਿਆਤਮਿਕ ਕਾਮਧੇਨੁ ਹੈ ਜਿਸ ਤੋਂ ਜੋ ਮੰਗੋ ਮਿਲਦਾ ਹੈ । ਸ੍ਰੀ ਵਿਆਸ ਜੀ (Shri Vyas ji) ਨੇ ਲਿਖਿਆ ਹੈ, “ਯੋਗ ਦਾ ਅਰਥ ਸਮਾਧੀ ਹੈ।”

ਉਪਰੋਕਤ ਵਿਚਾਰਾਂ ਤੋਂ ਪਤਾ ਚਲਦਾ ਹੈ ਕਿ ਯੋਗ ਦਾ ਸ਼ਬਦੀ ਭਾਵ ਜੋੜਨਾ ਹੈ । ਮਨੁੱਖੀ ਸਰੀਰ ਤੰਦਰੁਸਤ ਅਤੇ ਮਨ ਸ਼ੁੱਧ ਹੋਣ ਨਾਲ ਉਸ ਦਾ ਪਰਮਾਤਮਾ ਨਾਲ ਮੇਲ ਹੋ ਜਾਂਦਾ ਹੈ । ਯੋਗ ਰਾਹੀਂ ਸਰੀਰ ਅਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਮਨ ਦੀ ਇਕਾਗਰਤਾ ਵੱਧਦੀ ਹੈ । ਜਿਸ ਨਾਲ ਆਤਮਾ ਦਾ ਪਰਮਾਤਮਾ ਨਾਲ ਇਕਮਿਕ ਹੋਣਾ ਆਸਾਨ ਹੋ ਜਾਂਦਾ ਹੈ ।

‘‘ਯੋਗ ਵਿਗਿਆਨ ਨਾਲ ਮਨੁੱਖ ਸਰੀਰਕ, ਮਾਨਸਿਕ, ਬੌਧਿਕ ਅਤੇ ਅਧਿਆਤਮਿਕ ਤੌਰ ‘ਤੇ ਪੂਰਨ ਵਿਕਾਸ ਕਰ ਲੈਂਦਾ ਹੈ ।

(Yoga can be defined “Science of healthy and better Living physically, mentally, intellectually and spiritually.”)
ਇਸ ਤਰ੍ਹਾਂ ਆਤਮਾ ਦਾ ਪਰਮਾਤਮਾ ਨਾਲ ਮੇਲ ਯੋਗ ਹੈ । ਇਸ ਮਧੁਰ ਮੇਲ ਦਾ ਮਾਧਿਅਮ ਸਰੀਰ ਹੈ । ਤੰਦਰੁਸਤ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਸਰੀਰ ਦੇ ਸਦਕੇ ਹੀ ਆਤਮਾ ਦਾ ਪਰਮਾਤਮਾ ਨਾਲ ਮੇਲ ਹੋ ਸਕਦਾ ਹੈ ਅਤੇ ਉਸ ਸਰਬ ਸ਼ਕਤੀਮਾਨ ਦੇ ਦਰਸ਼ਨ ਹੋ ਸਕਦੇ ਹਨ | ਯੋਗ ਸਰੀਰ ਨੂੰ ਤੰਦਰੁਸਤ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣਾਉਂਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਯੋਗ ਆਤਮਾ ਪਰਮਾਤਮਾ ਨਾਲ ਇਕਮਿਕ ਕਰਨ ਦਾ ਵੱਡਾ ਸਾਧਨ ਹੈ । ਈਸ਼ਵਰ ਅਲੌਕਿਕ ਗੁਣਕਰਮ ਅਤੇ ਵਿਦਿਆਯੁਕਤ ਹੈ । ਇਹ ਆਕਾਸ਼ ਦੇ ਸਮਾਨ ਵਿਆਪਕ ਹੈ । ਜੀਵ ਅਤੇ ਈਸ਼ਵਰ ਵਿਚ ਇੱਕ ਦੂਸਰੇ ਨਾਲ ਸੰਬੰਧ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਯੋਗ ਇਹਨਾਂ ਸੰਬੰਧਾਂ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਨ ਵਿਚ ਸਹਾਇਕ ਹੁੰਦਾ ਹੈ ।

ਯੋਗ ਦਾ ਮਹੱਤਵ (Importance of Yoga)
ਯੋਗ ਵਿਗਿਆਨ ਦੀ ਮਨੁੱਖੀ ਜੀਵਨ ਲਈ ਬਹੁਤ ਮਹੱਤਤਾ ਹੈ । ਯੋਗ ਭਾਰਤ ਦਾ ਹੀ ਨਹੀਂ, ਸਗੋਂ ਦੁਨੀਆਂ ਦਾ ਪ੍ਰਾਚੀਨ ਗਿਆਨ ਹੈ । ਦੇਸ਼ਾਂ-ਵਿਦੇਸ਼ਾਂ ਵਿਚ ਡਾਕਟਰਾਂ ਅਤੇ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਅਧਿਆਪਕਾਂ ਨੇ ਇਸ ਗਿਆਨ ਦਾ ਸਿੱਕਾ ਮੰਨਿਆ ਹੈ । ਯੋਗ ਨਾਲ ਸਰੀਰ ਅਤੇ ਮਨ ਤੰਦਰੁਸਤ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਇਸਦੇ ਨਾਲ-ਨਾਲ ਨਾੜੀਆਂ ਵੀ ਲਚਕਦਾਰ ਅਤੇ ਮਜ਼ਬੂਤ ਰਹਿੰਦੀਆਂ ਹਨ । ਯੋਗ ਸਰੀਰ ਨੂੰ ਬਿਮਾਰੀ ਤੋਂ ਦੂਰ ਰੱਖਦਾ ਹੈ ਅਤੇ ਜੇ ਕੋਈ ਬਿਮਾਰੀ ਲੱਗ ਜਾਵੇ ਤਾਂ ਉਸ ਨੂੰ ਆਸਣ ਜਾਂ ਯੋਗ ਦੀਆਂ ਦੁਸਰੀਆਂ ਕਿਰਿਆਵਾਂ ਨਾਲ ਠੀਕ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਜਿੱਥੇ ਯੋਗ ਮਨੁੱਖ ਨੂੰ ਤੰਦਰੁਸਤ, ਸੁੰਦਰ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣਾਉਂਦਾ ਹੈ, ਉੱਥੇ ਇਹ ਸ਼ਖ਼ਸੀਅਤ ਨੂੰ ਚਾਰ ਚੰਨ ਲਾ ਦਿੰਦਾ ਹੈ ।

ਸੱਚ ਤਾਂ ਇਹ ਹੈ ਕਿ ਯੋਗ ਸਾਨੂੰ ਉਸ ਦੁਨੀਆਂ ਵਿਚ ਲੈ ਜਾਂਦਾ ਹੈ ਜਿੱਥੇ ਜੀਵਨ ਹੈ, ਤੰਦਰੁਸਤੀ ਹੈ, ਪਰਮ ਸੁੱਖ ਹੈ, ਮਨ ਦੀ ਸ਼ਾਂਤੀ ਹੈ । ਯੋਗ ਤਾਂ ਗਿਆਨ ਦੀ ਉਹ ਗੰਗਾ ਹੈ ਜਿਸ ਦੀ ਹਰੇਕ ਬੂੰਦ ਵਿਚ ਰੋਗ ਨਸ਼ਟ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਹੈ । ਯੋਗ ਪਰਮਾਤਮਾ ਦੇ ਨਾਲ ਮਿਲਣ ਦਾ ਸਰਵਉੱਤਮ ਸਾਧਨ ਹੈ | ਸਰੀਰ ਆਤਮਾ ਅਤੇ ਪਰਮਾਤਮਾ ਦੇ ਮਿਲਣ ਦਾ ਮਾਧਿਅਮ ਹੈ । ਇਕ ਤੰਦਰੁਸਤ ਸਰੀਰ ਦੁਆਰਾ ਹੀ ਪਰਮਾਤਮਾ ਦੇ ਦਰਸ਼ਨ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ | ਯੋਗ ਮਨੁੱਖ ਨੂੰ ਤੰਦਰੁਸਤ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣਾਉਣ ਦੇ ਨਾਲ ਉਸ ਨੂੰ ਸੁਯੋਗ ਅਤੇ ਗੁਣੀ ਵੀ ਬਣਾਉਂਦਾ ਹੈ । ਇਹ ਸਾਡੇ ਵਿਚ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਯੋਗ ਕੇਵਲ ਰੋਗੀ ਵਿਅਕਤੀਆਂ ਲਈ ਹੀ ਲਾਭਕਾਰੀ ਨਹੀਂ, ਸਗੋਂ ਸਵਸਥ ਮਨੁੱਖ ਵੀ ਇਸ ਦੇ ਅਭਿਆਸ ਤੋਂ ਲਾਭ ਉਠਾ ਸਕਦੇ ਹਨ । ਯੋਗ ਹਰ ਇੱਕ ਉਮਰ ਦੇ ਵਿਅਕਤੀਆਂ ਲਈ ਗੁਣਕਾਰੀ ਹੈ ।

ਯੋਗ ਦੇ ਅਭਿਆਸ ਨਾਲ ਸਰੀਰ ਦੇ ਸਾਰੇ ਅੰਗ ਠੀਕ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਨ ਲੱਗ ਪੈਂਦੇ ਹਨ | ਯੋਗ ਅਭਿਆਸ ਨਾਲ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਦਿਮਾਗੀ ਸੰਤੁਲਨ ਵਧਦਾ ਹੈ । ਯੋਗ ਦੀ ਜ਼ਰੂਰਤ ਅੱਜ ਦੇ ਯੁੱਗ ਵਿਚ ਵੀ ਉਨੀ ਹੀ ਹੈ ਜਿੰਨੀ ਪਹਿਲਾਂ ਦੇ ਯੁੱਗ ਵਿਚ ਸੀ । ਸਾਡੇ ਦੇਸ਼ ਨਾਲੋਂ ਬਾਹਰਲੇ ਦੇਸ਼ਾਂ ਵਿਚ ਇਸ ਖੇਤਰ ਵਿਚ ਬਹੁਤ ਉੱਨਤੀ ਹੋਈ ਹੈ । ਉਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਵਿਚ ਮਨ ਦੀ ਸ਼ਾਂਤੀ ਵਾਸਤੇ ਇਸ ਦਾ ਬਹੁਤ ਪ੍ਰਚਾਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਵਿਚ ਯੋਗ ਦੇ ਖੇਤਰ ਵਿਚ ਬਹੁਤ ਵਿਦਵਾਨ ਹਨ । ਇਹ ਧਾਰਨਾ ਵੀ ਗ਼ਲਤ ਹੈ ਕਿ ਅੱਜ-ਕਲ੍ਹ ਦੇ ਲੋਕ ਯੋਗ ਕਰਨ ਦੇ ਕਾਬਲ ਨਹੀਂ ਰਹੇ। ਅੱਜ ਦੇ ਯੁੱਗ ਵਿਚ ਵੀ ਮਨੁੱਖ ਯੋਗ ਤੋਂ ਪੂਰਾ ਲਾਭ ਉਠਾ ਸਕਦਾ ਹੈ ।

ਯੋਗ-ਵਿਗਿਆਨ ਵਿਅਕਤੀ ਦੇ ਸਰਵ-ਪੱਖੀ ਵਿਕਾਸ ਵਿਚ ਇਸ ਤਰ੍ਹਾਂ ਯੋਗਦਾਨ ਦਿੰਦਾ ਹੈ-
1. ਮਨੁੱਖ ਦੀਆਂ ਸਰੀਰਕ, ਮਾਨਸਿਕ ਅਤੇ ਬੁਨਿਆਦੀ ਸ਼ਕਤੀਆਂ ਦਾ ਵਿਕਾਸ (Development of Physical, Mental and Latent Powers of Man) – ਯੋਗ ਗਿਆਨ ਨਾਲ ਮਨੁੱਖ ਅਰੋਗ ਰਹਿ ਕੇ ਲੰਮੀ ਉਮਰ ਭੋਗਦਾ ਹੈ । ਯੋਗ, ਨਿਯਮ ਅਤੇ ਆਸਣ ਵਿਅਕਤੀ ਦੇ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਵਿਕਾਸ ਵਿਚ ਸਹਾਈ ਹੁੰਦੇ ਹਨ | ਆਸਣਾਂ ਵਿਚ ਸਰੀਰਕ ਕਿਰਿਆਵਾਂ ਦੇ ਕਰਨ ਨਾਲ ਮਨੁੱਖ ਦੇ ਸਰੀਰ ਦੇ ਸਾਰੇ ਅੰਗ ਹਰਕਤ ਵਿਚ ਆ ਜਾਂਦੇ ਹਨ । ਇਸ ਨਾਲ ਉਨ੍ਹਾਂ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਇਹਨਾਂ ਦਾ ਸਰੀਰ ਸੰਸਥਾਨਾਂ, ਜਿਵੇਂ ਪਾਚਨ-ਸੰਸਥਾਨ, ਸਾਹ ਸੰਸਥਾਨ ਅਤੇ ਮਾਸਪੇਸ਼ੀ ਸੰਸਥਾਨ ‘ਤੇ ਵੀ ਚੰਗਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ਅਤੇ ਵਿਅਕਤੀ ਦੀ ਕਾਰਜ ਯੋਗਤਾ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ | ਸਰੀਰਕ ਵਿਕਾਸ ਦੇ ਨਾਲ ਮਾਨਸਿਕ ਵਿਕਾਸ ਵੀ ਹੁੰਦਾ ਹੈ | ਪ੍ਰਾਣਾਯਾਮ ਅਤੇ ਅਸ਼ਟਾਂਗ ਯੋਗ ਨਾਲ ਮਨੁੱਖ ਦੀਆਂ ਗੁੱਝੀਆਂ ਤਾਕਤਾਂ (Latent Powers) ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ ।

2. ਸਰੀਰ ਦੀ ਅੰਦਰੂਨੀ ਸਫ਼ਾਈ (Internal cleanliness of Body) – ਯੋਗ ਦੀਆਂ ਛੇ ਅਵਸਥਾਵਾਂ ਨਾਲ ਸਰੀਰ ਸਰਵ-ਪੱਖੀ ਵਿਕਾਸ (All Round Development) ਕਰਦਾ ਹੈ । ਆਸਣਾਂ ਨਾਲ ਜਿੱਥੇ ਸਰੀਰ ਤੰਦਰੁਸਤ ਹੁੰਦਾ ਹੈ, ਉੱਥੇ ਮੁਦਰਾ-ਕਿਰਿਆਵਾਂ ਨਾਲ ਮਨ ਤੇ ਕਾਬੂ ਅਤੇ ਨਾੜੀ ਪੱਠਿਆਂ ਦਾ ਤਾਲਮੇਲ ਰਹਿੰਦਾ ਹੈ | ਪ੍ਰਾਣਾਯਾਮ ਨਾਲ ਸਰੀਰ ਚੁਸਤ ਅਤੇ ਅਰੋਗ ਰਹਿੰਦਾ ਹੈ । ਪ੍ਰਤਿਆਹਾਰ ਨਾਲ ਦਿੜਤਾ ਵਧਦੀ ਹੈ । ਧਿਆਨ ਅਤੇ ਸਮਾਧੀ ਨਾਲ ਮਨੁੱਖ ਦੁਨਿਆਵੀ ਭਟਕਣਾਂ ਤੋਂ ਉੱਪਰ ਉੱਠ ਜਾਂਦਾ ਹੈ ਅਤੇ ਉਸ ਦੀ ਆਤਮਾ ਪਰਮਾਤਮਾ ਵਿਚ ਲੀਨ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਧਿਆਨ, ਸਮਾਧੀ ਦੇ ਨਾਲ ਯਮਾਂ ਅਤੇ ਨਿਯਮਾਂ ਦੀ ਤਰ੍ਹਾਂ ਸ਼ਟਕਰਮ ਵੀ ਸਰੀਰ ਦੀ ਅੰਦਰੂਨੀ ਸਫ਼ਾਈ ਵਿਚ ਸਹਾਈ ਹੁੰਦੇ ਹਨ | ਸ਼ਟਕਰਮਾਂ ਵਿਚ ਧੋਤੀ, ਨੇਤੀ, ਬਸਤੀ, ਤਰਾਟਕ, ਨੌਲੀ, ਕਪਾਲ, ਛਾਤੀ, ਮਿਹਦੇ ਅਤੇ ਅੰਤੜੀਆਂ ਦੀ ਸਫ਼ਾਈ ਕਰਦੀਆਂ ਹਨ । ਆਤਮਾ ਨੂੰ ਪਰਮਾਤਮਾ ਨਾਲ ਮਿਲਾਉਣ ਦਾ ਮਾਧਿਅਮ ਸਰੀਰ ਹੈ ਅਤੇ ਸ਼ਟਰਮਾਂ, ਆਸਣਾਂ ਅਤੇ ਪ੍ਰਾਣਾਯਾਮ ਆਦਿ ਕਿਰਿਆਵਾਂ ਨਾਲ ਸਰੀਰ ਦੀ ਅੰਦਰੂਨੀ ਸਫ਼ਾਈ ਲਈ ਯੋਗ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।

3. ਸਰੀਰਕ ਅੰਗਾਂ ਵਿਚ ਮਜ਼ਬੂਤੀ ਅਤੇ ਉਨ੍ਹਾਂ ਵਿਚ ਲਚਕ ਲਿਆਉਣਾ (Development of Strength and elasticity) – ਇਹ ਅਕਸਰ ਦੇਖਣ ਵਿਚ ਆਉਂਦਾ ਹੈ ਕਿ ਯੋਗਿਕ ਕਿਰਿਆਵਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਵਿਅਕਤੀ ਦੀ ਸਿਹਤ ਉਹਨਾਂ ਵਿਅਕਤੀਆਂ ਨਾਲੋਂ ਕਿਤੇ ਚੰਗੀ ਹੁੰਦੀ ਹੈ ਜੋ ਯੋਗਿਕ ਕਿਰਿਆਵਾਂ ਵਿਚ ਰੁਚੀ ਨਹੀਂ ਰੱਖਦੇ । ਯੋਗ ਨਾਲ ਮਨੁੱਖ ਦਾ ਨਾ ਕੇਵਲ ਸਰੀਰਕ ਵਿਕਾਸ ਹੀ ਹੁੰਦਾ ਹੈ ਸਗੋਂ ਆਸਣਾਂ ਨਾਲ ਜੋੜਾਂ ਅਤੇ ਹੱਡੀਆਂ ਦਾ ਵਿਕਾਸ ਵੀ ਹੁੰਦਾ ਹੈ । ਖੂਨ ਦਾ ਦੌਰਾ ਤੇਜ਼ ਹੋ ਜਾਂਦਾ ਹੈ । ਧਨੁਰ ਆਸਨ ਅਤੇ ਹਲ ਆਸਣ ਰੀੜ੍ਹ ਦੀ ਲਚਕ ਵਧਾਉਣ ਵਿਚ ਸਹਾਇਕ ਹੁੰਦੇ ਹਨ ਜਿਸ ਕਰਕੇ ਮਨੁੱਖ ਜਲਦੀ ਬੁੱਢਾ ਨਹੀਂ ਹੁੰਦਾ । ਇਸ ਤਰ੍ਹਾਂ ਯੋਗ ਕਿਰਿਆਵਾਂ ਨਾਲ ਸਰੀਰ ਵਿਚ ਮਜ਼ਬੂਤੀ ਅਤੇ ਅੰਗਾਂ ਵਿਚ ਲਚਕ ਆਉਂਦੀ ਹੈ ।

4. ਭਾਵਾਤਮਕ ਵਿਕਾਸ (Emotional Development) – ਅਜੋਕਾ ਮਨੁੱਖ ਮਾਨਸਿਕ ਅਤੇ ਆਤਮਿਕ ਸ਼ਾਂਤੀ ਦੀ ਕਾਮਨਾ ਕਰਦਾ ਹੈ । ਅਕਸਰ ਦੇਖਣ ਵਿਚ ਆਇਆ ਹੈ ਕਿ ਅਸੀਂ ਆਪਣੀਆਂ ਭਾਵਨਾਵਾਂ ਦੇ ਰੌਂਅ ਵਿਚ ਵਹਿ ਕੇ ਕਦੇ ਤਾਂ ਉਦਾਸੀ ਦੇ ਸਾਗਰ ਵਿਚ ਡੁੱਬ ਜਾਂਦੇ ਹਾਂ ਅਤੇ ਕਦੇ ਖੁਸ਼ੀ ਦੇ ਮਾਰੇ ਪਾਗਲ ਜਿਹੇ ਹੋ ਜਾਂਦੇ ਹਾਂ | ਕਦੇ ਇੱਕ ਸਾਧਾਰਨ ਜਿਹੀ ਅਸਫਲਤਾ ਜਾਂ ਦੁਖਦਾਈ ਘਟਨਾ ਸਾਨੂੰ ਇੰਨਾ ਗ਼ਮਗੀਨ ਬਣਾ ਦਿੰਦੀ ਹੈ ਕਿ ਸੰਸਾਰ ਦੀ ਕੋਈ ਵਸਤੁ ਸਾਨੂੰ ਚੰਗੀ ਨਹੀਂ ਲੱਗਦੀ | ਸਾਨੂੰ ਜੀਵਨ ਰੁੱਖਾ ਅਤੇ ਭਾਰਾ ਜਿਹਾ ਜਾਪਦਾ ਹੈ । ਇਸ ਦੇ ਉਲਟ ਕਈ ਵਾਰ ਸਾਧਾਰਨ ਜਿਹੀ ਸਫਲਤਾ ਜਾਂ ਖ਼ੁਸ਼ੀ ਦੀ ਗੱਲ ਸਾਨੂੰ ਇੰਨਾ ਪਸੰਨ ਕਰ ਦਿੰਦੀ ਹੈ ਕਿ ਸਾਡੇ ਪੈਰ ਧਰਤੀ ‘ਤੇ ਨਹੀਂ ਟਿਕਦੇ । ਅਸੀਂ ਆਪਣਾ ਮਾਨਸਿਕ ਸੰਤੁਲਨ ਗੁਆ ਬੈਠਦੇ ਹਾਂ । ਇਹਨਾਂ ਗੱਲਾਂ ਵਿਚ ਸਾਡੀ ਭਾਵਾਤਮਕ ਅਪਕਿਆਈ (Emotional Immaturity) ਦੀ ਝਲਕ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ ।

ਯੋਗ ਸਾਨੂੰ ਆਪਣੀਆਂ ਭਾਵਨਾਵਾਂ ‘ਤੇ ਕੰਟਰੋਲ ਰੱਖਣ ਅਤੇ ਸੰਤੁਲਨ ਵਿਚ ਰਹਿਣਾ ਸਿਖਾਉਂਦਾ ਹੈ । ਇਹ ਸਾਨੂੰ ਇਹ ਸਿਖਾਉਂਦਾ ਹੈ ਕਿ ਅਸਫਲਤਾ ਜਾਂ ਸਫਲਤਾ ਖ਼ੁਸ਼ੀ ਜਾਂ ਗ਼ਮੀ ਇਕੋ ਸਿੱਕੇ ਦੇ ਦੋ ਪਹਿਲੂ (Two sides of the same Coin) ਹਨ । ਇਹ ਜੀਵਨ ਗਮਾਂ ਅਤੇ ਖ਼ੁਸ਼ੀਆਂ ਦਾ ਅਨੋਖਾ ਸੰਗਮ ਹੈ । ਗ਼ਮਾਂ ਅਤੇ ਖ਼ੁਸ਼ੀਆਂ ਨਾਲ ਸਮਝੌਤਾ ਕਰਨਾ ਹੀ ਸੁਖੀ ਜੀਵਨ ਦਾ ਰਾਜ਼ ਹੈ । ਸਾਨੂੰ ਆਪਣੇ ਜੀਵਨ ਦੀ ਜਿੱਤ ਅਤੇ ਹਾਰ ਨੂੰ ਸਫਲਤਾ ਅਤੇ ਅਸਫ਼ਲਤਾ ਨੂੰ, ਗ਼ਮ ਅਤੇ ਖ਼ੁਸ਼ੀ ਨੂੰ ਖਿੜੇ ਮੱਥੇ ਪ੍ਰਵਾਨ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਜੇਕਰ ਕਿਸਮਤ ਨਾਲ ਸਫਲਤਾ ਸਾਡੇ ਕਦਮ ਚੁੰਮਦੀ ਹੈ ਤਾਂ ਸਾਨੂੰ ਖ਼ੁਸ਼ੀ ਦੇ ਮਾਰੇ ਆਪਣੇ ਆਪੇ ਤੋਂ ਬਾਹਰ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ । ਇਸ ਦੇ ਉਲਟ ਜੇ ਸਾਨੂੰ ਅਸਫਲਤਾ ਦਾ ਮੂੰਹ ਦੇਖਣਾ ਪੈਂਦਾ ਹੈ ਤਾਂ ਸਾਨੂੰ ਆਪਣਾ ਮੂੰਹ ਲਟਕਾਉਣਾ ਨਹੀਂ ਚਾਹੀਦਾ । ਇਸ ਤਰ੍ਹਾਂ ਯੋਗ ਕਿਰਿਆਵਾਂ ਦਾ ਭਾਵਾਤਮਕ ਵਿਕਾਸ ਲਈ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵ ਹੈ ।

5. ਬਿਮਾਰੀਆਂ ਦੀ ਰੋਕਥਾਮ ਅਤੇ ਰੋਗਾਂ ਤੋਂ ਕੁਦਰਤੀ ਬਚਾਅ (Prevention of Diseases and Immuniza tion) – ਯੋਗ ਕਿਰਿਆਵਾਂ ਨਾਲ ਬਿਮਾਰੀਆਂ ਤੋਂ ਬਚਾਅ ਹੁੰਦਾ ਹੈ । ਜੇਕਰ ਕਿਸੇ ਕਾਰਨ ਬਿਮਾਰੀਆਂ ਲੱਗ ਜਾਣ ਤਾਂ ਉਨ੍ਹਾਂ ਤੋਂ ਛੁਟਕਾਰਾ ਪਾਉਣ ਦੇ ਢੰਗ ਅਤੇ ਰੋਗਾਂ ਤੋਂ ਕੁਦਰਤੀ ਬਚਾਅ ਯੋਗ ਵਿਚ ਸ਼ਾਮਲ ਹਨ । ਰੋਗਾਂ ਦੇ ਕੀਟਾਣੁ (Germs of Bacteria) ਇੱਕ ਮਨੁੱਖ ਤੋਂ ਦੂਜੇ ਮਨੁੱਖ ਦੇ ਸਰੀਰ ‘ਤੇ ਹਮਲਾ ਕਰਕੇ ਬਿਮਾਰੀਆਂ ਫੈਲਾਉਂਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਰੋਗਾਂ ਤੋਂ ਬਚਾਅ ਕਰਨ ਦੇ ਢੰਗ, ਭਾਵ ਰੋਗਾਂ ਦਾ ਮੁਕਾਬਲਾ ਕਿਵੇਂ ਕੀਤਾ ਜਾਵੇ, ਰੋਗਾਂ ਤੋਂ ਛੁਟਕਾਰਾ ਕਿਵੇਂ ਪਾਇਆ ਜਾਵੇ ਅਤੇ ਮਨੁੱਖ ਨੂੰ ਅਰੋਗ ਕਿਵੇਂ ਰੱਖਿਆ ਜਾਵੇ, ਇਹ ਆਸਣ, ਧੋਤੀ, ਨੌਲੀ ਆਦਿ ਜਿਨ੍ਹਾਂ ਨਾਲ ਅੰਦਰੂਨੀ ਅੰਗ ਸਾਫ਼ ਹੁੰਦੇ ਹਨ, ਯੋਗ ਗਿਆਨ ਹੀ ਦੱਸਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਯੋਗ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ? (What precautions are needed to be taken before performing yoga ?)
ਉੱਤਰ-
ਯੋਗ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਹੇਠ ਲਿਖੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ।

1. ਯੋਗ ਆਸਣ ਕਰਨ ਵੇਲੇ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਸੂਰਜ ਨਮਸਕਾਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
2. ਯੋਗ ਆਸਣ ਕਰਨ ਦੀ ਥਾਂ ਸਮਤਲ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਜ਼ਮੀਨ ਤੇ ਦਰੀ ਜਾਂ ਕੰਬਲ ਵਿਛਾ ਕੇ ਯੋਗ ਆਸਣ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ ।
3. ਯੋਗ ਆਸਣ ਕਰਨ ਦੀ ਥਾਂ, ਸ਼ਾਂਤ, ਹਵਾਦਾਰ ਅਤੇ ਸਾਫ਼ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
4. ਆਸਣ ਕਰਦੇ ਸਮੇਂ ਸਾਹ ਨਾਰਮਲ ਅਤੇ ਮਨ ਸ਼ਾਂਤ ਰੱਖਣਾ ਜ਼ਰੂਰੀ ਹੈ ।
5. ਖਾਣਾ ਖਾਣ ਤੋਂ ਘੱਟੋ-ਘੱਟ ਚਾਰ ਘੰਟੇ ਬਾਅਦ ਚਿਤ ਨੂੰ ਏਕਾਗਰ ਕਰਕੇ ਯੋਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
6. ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਆਰਾਮਦਾਇਕ ਅਤੇ ਫਿਰ ਸਭਿਆਚਾਰਕ ਆਸਣ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ ।
7. ਅਭਿਆਸ ਹੌਲੇ-ਹੌਲੇ ਸਰਲਤਾਪੂਰਵਕ ਕਰਨਾ ਅਤੇ ਹੌਲੇ-ਹੌਲੇ ਅਭਿਆਸ ਨੂੰ ਵਧਾਉਣਾ ਹੁੰਦਾ ਹੈ ।
8. ਪ੍ਰਤੀ ਦਿਨ ਅਭਿਆਸ ਸਿਖਿਅਕ ਦੀ ਦੇਖ-ਰੇਖ ਵਿਚ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
9. ਦੋ ਆਸਣਾਂ ਵਿਚਕਾਰ ਥੋੜਾ ਵਿਸ਼ਰਾਮ, ਸ਼ਵ ਆਸਣ ਕਰਕੇ ਕਰਨਾ ਹੁੰਦਾ ਹੈ ।
10. ਸਰੀਰ ਤੇ ਘੱਟੋ-ਘੱਟ ਕੱਪੜੇ ਲੰਗੋਟ, ਨਿੱਕਰ, ਬਨੈਣ, ਪਹਿਨਣਾ ਸੰਤੁਲਿਤ ਤੇ ਹਲਕਾ ਭੋਜਨ ਕਰਨਾ ਹੁੰਦਾ ਹੈ ।
11. ਯੋਗ ਕਰਨ ਸਮੇਂ ਸਾਹ ਅੰਦਰ ਅਤੇ ਬਾਹਰ ਕੱਢਣ ਦੀ ਕਿਰਿਆ ਦੀ ਤਰਤੀਬ ਠੀਕ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
12. ਯੋਗ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਮੌਸਮ ਦੇ ਅਨੁਸਾਰ ਗਰਮ ਜਾਂ ਠੰਡੇ ਪਾਣੀ ਨਾਲ ਨਹਾ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ ਜਾਂ ਫਿਰ ਬਾਅਦ ਵਿਚ ਘੱਟ ਤੋਂ ਘੱਟ ਅੱਧੇ ਘੰਟੇ ਦਾ ਅੰਤਰਾਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਸੂਰਜ ਨਮਸਕਾਰ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਇਸ ਦੇ ਕੁੱਲ ਕਿੰਨੇ ਅੰਗ ਹਨ ? (What is meant by “Surya Namaskara’? How many parts does have in total ?)
ਉੱਤਰ-
ਸੂਰਜ ਤੋਂ ਭਾਵ ਸੁਰਜ ਅਤੇ ਨਮਸਕਾਰ ਤੋਂ ਭਾਵ ਪ੍ਰਣਾਮ ਤੋਂ ਹੈ । ਕਿਰਿਆ ਕਰਦੇ ਹੋਏ ਸੂਰਜ ਨੂੰ ਪ੍ਰਣਾਮ ਕਰਨਾ ਸੂਰਜ ਨਮਸਕਾਰ ਅਖਵਾਉਂਦਾ ਹੈ । ਸੂਰਜ ਨਮਸਕਾਰ ਵਿਚ ਕੁੱਲ 12 ਕਿਰਿਆਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਕਿ ਕਸਰਤ ਕਰਦੇ ਹੋਏ ਪੂਰੇ ਸਰੀਰ ਦੀ ਲਚਕ ਵਧਾਉਣ ਵਿਚ ਮਦਦ ਕਰਦੀਆਂ ਹਨ । ਸੂਰਜ ਨਮਸਕਾਰ ਕਰਨ ਦੀ ਵਿਧੀ ਇਸ ਪ੍ਰਕਾਰ ਹੈ ।

ਸੂਰਜ ਨਮਸਕਾਰ
ਢੰਗ-
ਸਥਿਤੀ-1: ਪ੍ਰਣਾਮਾਸਨ

1. ਜੇ ਸੰਭਵ ਹੋ ਸਕੇ ਤਾਂ ਸੂਰਜ ਵੱਲ ਮੂੰਹ ਕਰਕੇ ਖੜੇ ਹੋਵੋ ।
2. ਪੈਰ ਸਿੱਧੇ ਅਤੇ ਹਥੇਲੀ ਨੂੰ ਛਾਤੀ ਦੇ ਕੇਂਦਰ ਵਿਚ ਅਰਾਮ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਰੱਖੋ ।
3. ਚੇਤਨਾ ਵਿੱਚ ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਲੈਂਦੇ ਰਹੋ ।
4. ਸਰੀਰ ਨੂੰ ਬਿਲਕੁੱਲ ਢਿੱਲਾ ਅਤੇ ਪਿੱਠ ਸਿੱਧੀ ਰੱਖੋ ।

ਲਾਭ : ਇਸ ਸਥਿਤੀ ਵਿੱਚ ਧਿਆਨ ਅਤੇ ਸ਼ਾਂਤੀ ਨੂੰ ਬਣਾਉਣ ਵਿੱਚ ਮਦਦ ਮਿਲਦੀ ਹੈ ।

ਸਥਿਤੀ-2: ਹਸਤ ਉਥਾਂਨਾਸਨ

1. ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਲੈਂਦੇ ਹੋਏ ਬਾਂਹਵਾਂ ਨੂੰ ਉੱਪਰ ਵੱਲ ਲੈ ਕੇ ਜਾਓ । ਬਾਂਹਵਾਂ ਨੂੰ ਮੋਢਿਆਂ ਦੀ ਚੌੜਾਈ ਤੇ ਖੋਲ੍ਹ ਕੇ ਰੱਖੋ ।
2. ਪਿੱਠ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਪਿੱਛੇ ਵੱਲ ਖਿੱਚੋ ਅਤੇ ਹੌਲੀ-ਹੌਲੀ ਬਾਂਹਵਾਂ ਪਿੱਛੇ ਵੱਲ ਲੈ ਕੇ ਜਾਓ ।
3. ਹੌਲੀ-ਹੌਲੀ ਅਭਿਆਸ ਨਾਲ ਕਮਰ ਵਿਚ ਲਚਕਤਾ ਆ ਜਾਵੇਗੀ | ਅਭਿਆਸ ਨਾਲ ਕਮਰ ਵਿੱਚ ਲਚਕਤਾ ਆ ਜਾਵੇਗੀ ।

ਲਾਭ : ਇਸ ਆਸਨ ਨਾਲ ਪੈਰ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਚੰਗੀ ਤਰ੍ਹਾਂ ਖੁੱਲ੍ਹ ਕੇ ਫੈਲ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਬਾਂਹਵਾਂ, ਮੋਢੇ ਅਤੇ ਰੀੜ ਦੀ ਹੱਡੀ ਟੋਨ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਸ ਦੇ ਅਭਿਆਸ ਨਾਲ ਫੇਫੜੇ ਵੀ ਖੁੱਲ੍ਹ ਜਾਂਦੇ ਹਨ ।

ਸਥਿਤੀ-3 : ਪਦਹਸਤਾਨਾਸਨ

1. ਸਾਹ ਬਾਹਰ ਛੱਡਦੇ ਹੋਏ ਅੱਗੇ ਵੱਲ ਨੂੰ ਝੁਕੋ, ਲੱਤਾਂ ਸਿੱਧੀਆਂ ਰੱਖੋ ਅਤੇ ਆਪਣੇ ਹੱਥਾਂ ਦੀਆਂ ਉਂਗਲਾਂ ਨਾਲ ਫ਼ਰਸ਼ ਨੂੰ ਛੂਹਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੋ ।
2. ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਨੂੰ ਕਮਰ ਦੇ ਜੋੜ ਤੋਂ ਓਨਾ ਝੁਕਾਓ ਜਿਸ ਨਾਲ ਕਿ ਦਰਦ ਮਹਿਸੂਸ ਨਾ ਹੋਵੇ ਜਾਂ ਫਿਰ ਜਿੰਨਾ ਝੁਕਿਆ ਜਾ ਸਕੇ ।

ਲਾਭ : ਇਸ ਆਸਣ ਨਾਲ ਪੇਟ ਦੀਆਂ ਕਈ ਬਿਮਾਰੀਆਂ ਤੋਂ ਮੁਕਤੀ ਮਿਲਦੀ ਹੈ ਅਤੇ ਅਰਾਮ ਪਹੁੰਚਾਉਂਦਾ ਹੈ । ਇਹ ਪੇਟ ਦੀ ਵਾਧੂ ਚਰਬੀ ਨੂੰ ਘਟਾਉਂਦਾ ਹੈ ।

ਸਥਿਤੀ-4: ਅਸ਼ਵਾ ਸੰਚਲੇਸਣਨਾ

1. ਹੱਥਾਂ ਦੀਆਂ ਉਂਗਲਾਂ ਨਾਲ ਫ਼ਰਸ਼ ਨੂੰ ਛੁਹਾਉਂਦੇ ਹੋਏ ਖੱਬੀ ਲੱਤ ਮੋੜਦੇ ਹੋਏ ਸੱਜੀ ਲੱਤ ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਸਿੱਧਾ ਲੈ ਕੇ ਜਾਓ।
2. ਰੀੜ ਦੀ ਹੱਡੀ ਤੇ ਸਿਰ ਨੂੰ ਸਿੱਧਾ ਰੱਖਦੇ ਹੋਏ ਪੀਰੇ ਅਰਕ ਬਣਾਓ ਅਤੇ ਉੱਪਰ ਦੇਖੋ ।

ਲਾਭ : ਇਹ ਆਸਣ ਢਿੱਡ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਨੂੰ ਫੋਨ ਕਰਦਾ ਹੈ ਅਤੇ ਲੱਤ ਅਤੇ ਪੈਰ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦਾ ਹੈ ।

ਸਥਿਤੀ-5 : ਪਰਵਤਾਸਨਾ

1. ਸਾਹ ਬਾਹਰ ਛੱਡਦੇ ਹੋਏ, ਖੱਬੀ ਲੱਤ ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਸੱਜੀ ਲੱਤ ਵੱਲ ਸਿੱਧਾ ਰੱਖੋ ।
2. ਸਿਰ ਨੂੰ ਦੋਵੇਂ ਬਾਂਹਵਾਂ ਦੇ ਵਿਚਕਾਰ ਰੱਖਦੇ ਹੋਏ ਸਰੀਰ ਦੇ ਸਾਰੇ ਭਾਰ ਨੂੰ ਬਾਂਹਵਾਂ ਅਤੇ ਪੈਰਾਂ ਤੇ ਪਾਉ ਅਤੇ ਇਹ ਸਥਿਤੀ ਬਣਾ ਕੇ ਰੱਖੋ ।

ਲਾਭ : ਇਹ ਆਸਣ ਮੋਢਿਆਂ ਅਤੇ ਗਰਦਨ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਨੂੰ ਫੋਨ ਕਰਦਾ ਹੈ । ਲੱਤਾਂ ਅਤੇ ਬਾਂਹਵਾਂ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਨੂੰ ਵੀ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦੀ ਹੈ ।

ਸਥਿਤੀ-6 : ਅਸ਼ਟਾਂਗ ਆਸਨ

1. ਪਿਛਲੇ ਆਸਨ ਤੋਂ ਹੌਲੀ ਗੋਡਿਆਂ ਨੂੰ ਜ਼ਮੀਨ ਵੱਲ ਲੈ ਕੇ ਆਓ ।
2. ਛਾਤੀ ਅਤੇ ਠੋਡੀ ਨੂੰ ਜ਼ਮੀਨ ਨਾਲ ਛੂਹਵੋ ।
3. ਦੋਵੇਂ ਬਾਂਹਵਾਂ ਨੂੰ ਛਾਤੀ ਦੇ ਬਰਾਬਰ ਮੋੜ ਕੇ ਰੱਖੋ ਅਤੇ ਚੁੱਲ੍ਹਿਆਂ ਨੂੰ ਜ਼ਮੀਨ ਤੋਂ ਉੱਪਰ ਵੱਲ ਖਿੱਚ ਕੇ ਰੱਖੋ ।

ਲਾਭ : ਇਹ ਆਸਣ ਮੋਢੇ ਅਤੇ ਗਰਦਨ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਨੂੰ ਫੋਨ ਕਰਦਾ ਹੈ । ਲੱਤ ਅਤੇ ਹੱਥ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦਾ ਹੈ ਅਤੇ ਛਾਤੀ ਨੂੰ ਵਿਕਸਿਤ ਕਰਦਾ ਹੈ ।

ਸਥਿਤੀ-7 : ਭੂਜੰਗਾਸਨ

1. ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਅੰਦਰ ਲੈਂਦੇ ਹੋਏ ਲੱਤਾਂ ਅਤੇ ਕਮਰ ਨੂੰ ਜ਼ਮੀਨ ਤੇ ਰੱਖੋ ।
2. ਬਾਂਹਵਾਂ ਨੂੰ ਖਿੱਚਦੇ ਹੋਏ ਛਾਤੀ ਵਾਲੇ ਭਾਗ ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਖਿੱਚੋ ।
3. ਸਿਰ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਪਿੱਛੇ ਵੱਲ ਲੈ ਕੇ ਜਾਓ ।

ਲਾਭ : ਇਹ ਆਸਣ ਪੇਟ ਵੱਲ ਲਹੂ ਗੇੜ ਨੂੰ ਤੇਜ਼ ਕਰਦਾ ਹੈ ਅਤੇ ਕਈ ਪੇਟ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਤੋਂ ਛੁਟਕਾਰਾ ਦਿਲਾਉਂਦਾ ਹੈ ਜਿਵੇਂ ਕਿ ਬਦਹਜ਼ਮੀ, ਕਬਜ਼ ਆਦਿ । ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਨੂੰ ਮਜ਼ਬੂਤੀ ਮਿਲਦੀ ਹੈ ਅਤੇ ਲਹੂ ਗੇੜ ਵਿੱਚ ਸੁਧਾਰ ਹੁੰਦਾ ਹੈ ।

ਸਥਿਤੀ-8 : ਪਰਵਤਾਸਨਾ

1. ਹੌਲੀ-ਹੌਲੀ ਦੋਵੇਂ ਪੈਰਾਂ ਤੇ ਵਾਪਿਸ ਜਾ ਕੇ ਸਿੱਧੇ ਖੜੇ ਹੋ ਜਾਵੋ ।
2. ਛਾਤੀ ਵਾਲੇ ਭਾਗਾਂ ਨੂੰ ਪੇਟ ਵੱਲ ਲੈ ਕੇ ਜਾਓ ਅਤੇ ਦੋਵੇ ਹੱਥਾਂ ਨਾਲ ਜ਼ਮੀਨ ਨੂੰ ਛੂਹਵੋ । ਇਹ ਬਿਲਕੁੱਲ 5ਵੀਂ ਸਥਿਤੀ | ਵਾਂਗ ਹੋ ਜਾਵੇਗਾ |

ਸਥਿਤੀ-9 : ਅਸ਼ਵਾ ਸੰਚਲੇਸਣਨਾ
1. ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਅੰਦਰ ਲੈਂਦੇ ਹੋਏ ਸੱਜੇ ਪੈਰ ਨੂੰ ਦੋਵੇਂ ਹੱਥਾਂ ਦੇ ਵਿਚਕਾਰ ਲੈ ਕੇ ਆਵੋ ਅਤੇ ਖੱਬੀ ਲੱਤ ਨੂੰ ਪਿੱਛੇ ਵੱਲ | ਸਿੱਧਾ ਰੱਖੋ । ਇਸ ਦੇ ਨਾਲ ਹੀ ਮੋਢੇ ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਸਿੱਧੇ ਖਿੱਚੋ ਅਤੇ ਛਾਤੀ ਵਾਲੇ ਭਾਗ ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਲੈ ਕੇ ਜਾਓ ਅਤੇ ਪਿੱਠ ਦਾ ਆਰਕ ਬਣਾਓ ।

ਸਥਿਤੀ-10 : ਪਦਹਸਤਾਨਾਸਨ
1. ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਛੱਡਦੇ ਹੋਏ ਦੋਵੇਂ ਲੱਤਾਂ ਨੂੰ ਸਿੱਧਾ ਰੱਖੋ ਅਤੇ ਹੱਥਾਂ ਨਾਲ ਫ਼ਰਸ਼ ਨੂੰ ਛੂਹਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੋ । ਇਹ ਕਰਦੇ ਸਮੇਂ ਗੋਡੇ ਸਿੱਧੇ ਹੋਣ ।

ਸਥਿਤੀ-11 : ਹਸਤ ਉਥਾਂਨਾਸਨ

1. ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਲੈਂਦੇ ਹੋਏ ਬਾਂਹਵਾਂ ਨੂੰ ਉੱਪਰ ਵੱਲ ਲੈ ਕੇ ਜਾਓ । ਬਾਂਹਵਾਂ ਨੂੰ ਮੋਢਿਆਂ ਦੀ ਚੌੜਾਈ ਤੇ ਖੋਲ੍ਹ ਕੇ ਰੱਖੋ ।
2. ਪਿੱਠ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਪਿੱਛੇ ਵੱਲ ਖਿੱਚੋ ਅਤੇ ਹੌਲੀ-ਹੌਲੀ ਬਾਂਹਵਾਂ ਪਿੱਛੇ ਵੱਲ ਲੈ ਕੇ ਜਾਓ ।
3. ਅਭਿਆਸ ਨਾਲ ਕਮਰ ਵਿੱਚ ਲਚਕਤਾ ਆ ਜਾਵੇਗੀ ।

ਸਥਿਤੀ-12: ਪ੍ਰਣਾਮਾਸਨ ,

1. ਪੈਰ ਸਿੱਧੇ ਅਤੇ ਹਥੇਲੀ ਨੂੰ ਛਾਤੀ ਦੇ ਕੇਂਦਰ ਵਿਚ ਅਰਾਮ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਰੱਖੋ ।
2. ਚੇਤਨਾ ਵਿੱਚ ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਲੈਂਦੇ ਰਹੋ ।
3. ਸਰੀਰ ਬਿਲਕੁੱਲ ਢਿੱਲਾ ਅਤੇ ਪਿੱਠ ਸਿੱਧੀ ਰੱਖੋ ।

ਲਾਭ :

1. ਸੂਰਜ ਨਮਸਕਾਰ ਲਚਕ, ਸ਼ਕਤੀ ਅਤੇ ਤਾਕਤ ਵਿਚ ਵਾਧਾ ਕਰਦਾ ਹੈ ।
2. ਸੂਰਜ ਨਮਸਕਾਰ ਮਨ ਦੀ ਇਕਾਗਰਤਾ ਵਧਾਉਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।
3. ਇਸ ਨਾਲ ਵਧੀ ਹੋਈ ਚਰਬੀ ਸਰੀਰ ਵਿਚੋਂ ਖ਼ਤਮ ਹੋ ਜਾਂਦੀ ਹੈ ।
4. ਇਸ ਆਸਨ ਨਾਲ ਬੱਚਿਆਂ ਦਾ ਕੱਦ ਵੱਧ ਜਾਂਦਾ ਹੈ ।
5. ਇਸ ਆਸਨ ਨਾਲ ਸਰੀਰ ਵਿਚ ਖੂਨ ਦਾ ਦੌਰਾ ਵੱਧ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਕੋਈ ਇਕ ਆਰਾਮਦਾਇਕ ਅਤੇ ਸਭਿਆਚਾਰਕ ਆਸਣ ਦੀ ਵਿਧੀ ਅਤੇ ਲਾਭ ਬਾਰੇ ਵਿਸਥਾਰ ਪੂਰਵਕ ਲਿਖੋ । (Write in detail the method and benefits of any one of Relaxative and Cultural asana.)
ਉੱਤਰ-
ਸੁਖ ਆਸਣ ਜਾਂ ਸਿੱਧ ਆਸਣ/ਸਭਿਆਚਾਰਕ ਆਸਣ (Sukh Asana Or Siddhasana)
ਇਹ ਆਸਣ ਕੱਪੜੇ ਸਿਉਣ ਵਾਲੇ ਦਰਜੀ ਦੇ ਬੈਠਣ ਦੀ ਸੀਟ ਵਾਂਗ ਹੁੰਦਾ ਹੈ । ਦਰਜੀ ਦੀ ਤਰ੍ਹਾਂ ਲੱਤਾਂ ਦੀ ਚੌਕੜੀ ਮਾਰ ਕੇ ਬੈਠਿਆ ਜਾਂਦਾ ਹੈ ।
ਸਥਿਤੀ (Position) – ਸੁਖ ਆਸਣ ਦੀ ਸਥਿਤੀ ਅਰਧ ਪਦਮ ਆਸਣ ਵਰਗੀ ਹੁੰਦੀ ਹੈ ।

ਵਿਧੀ (Technique) – ਪੈਰਾਂ ਦੇ ਭਾਰ ਬੈਠਕੇ ਚੌਕੜੀ ਮਾਰਨ ਵੇਲੇ ਸੱਜੇ ਪੈਰ ਨੂੰ ਖੱਬੇ ਪੈਰ ਹੇਠਾਂ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖੋ ਕਿ ਤੁਹਾਡੇ ਸੱਜੇ ਪੈਰ ਦੀ ਅੱਡੀ ਖੱਬੇ ਪੈਰ ਨੂੰ ਛੁਹੇ । ਇਸ ਤੋਂ ਮਗਰੋਂ ਖੱਬੇ ਪੈਰ ਨੂੰ ਚੁੱਕੋ ਅਤੇ ਸੱਜੇ ਪੈਰ ਦੇ ਅੱਗੇ ਰੱਖੋ । ਆਪਣੇ ਦੋਵੇ ਹੱਥ ਗੋਡਿਆਂ ਤੇ ਰੱਖੋ । ਜਿਸ ਨਾਲ ਗੁੱਟ ਉਸ ਉਪਰ ਹੋਣ ਅਤੇ ਹਥੇਲੀਆਂ ਉੱਪਰ ਨੂੰ ਹੋ ਜਾਣ । ਅੰਗੂਠੇ ਦਾ ਪੋਟਾ ਵਿਚਕਾਰਲੀ ਉਂਗਲ ਦੇ ਪੋਟੇ ਨਾਲ ਛੂਹਦਾ ਹੋਵੇ ।

ਲਾਭ (Advantages) –

1. ਇਹ ਆਸਣ ਮਨ ਦੀ ਇਕਾਗਰਤਾ ਵਿਚ ਵਾਧਾ ਕਰਦਾ ਹੈ ।
2. ਇਹ ਧਿਆਨ ਲਗਾਉਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।
3. ਇਸ ਨਾਲ ਰੀੜ ਦੀ ਹੱਡੀ ਦਾ ਦਰਦ ਦੂਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਜੋੜਾਂ ਦੀ ਅਕੜਨ ਠੀਕ ਹੁੰਦੀ ਹੈ ।
4. ਮੂਤਰ ਨਾਲ ਸੰਬੰਧਿਤ ਰੋਗ ਦੂਰ ਹੁੰਦੇ ਹਨ ।
5. ਮਨ ਨੂੰ ਸ਼ਾਂਤੀ ਦਿੰਦਾ ਹੈ ਅਤੇ ਚਿਹਰੇ ਤੇ ਰੌਣਕ ਲਿਆਉਂਦਾ ਹੈ ।
6. ਨਾੜੀ ਪ੍ਰਣਾਲੀ ਚੁਸਤ ਤੇ ਦਰੁੱਸਤ ਤੇ ਲਚਕੀਲੀ ਰਹਿੰਦੀ ਹੈ ।

ਸ਼ਵ ਆਸਣ (ਅਰਾਮਦਾਇਕ ਆਸਣ (Shavasana) – ਸ਼ਵ ਆਸਣ ਵਿਚ ਪਿੱਠ ਦੇ ਬਲ ਸਿੱਧਾ ਲੇਟ ਕੇ ਸਰੀਰ ਨੂੰ ਢਿੱਲਾ ਛੱਡ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਸ਼ਵ ਆਸਣ ਕਰਨ ਲਈ ਜ਼ਮੀਨ ਤੇ ਪਿੱਠ ਦੇ ਬਲ ਲੇਟ ਜਾਓ ਅਤੇ ਸਰੀਰ ਨੂੰ ਬਿਲਕੁਲ ਢਿੱਲਾ ਛੱਡ ਦਿਓ । ਹੌਲੀ-ਹੌਲੀ ਲੰਬੇ-ਲੰਬੇ ਸਾਹ ਲਵੋ । ਬਿਲਕੁਲ ਚਿੱਤ ਲੇਟ ਕੇ ਸਾਰੇ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਨੂੰ ਬਹੁਤ ਢਿੱਲਾ ਛੱਡ ਦਿਓ । ਦੋਹਾਂ ਪੈਰਾਂ ਵਿਚ ਡੇਢ ਫੁੱਟ ਦੀ ਦੂਰੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਹੱਥਾਂ ਦੀਆਂ ਹਥੇਲੀਆਂ ਆਕਾਸ਼ ਵੱਲ ਕਰਕੇ ਸਰੀਰ ਤੋਂ ਦੂਰ ਰੱਖੋ | ਅੱਖਾਂ ਬੰਦ ਕਰਕੇ ਅੰਤਰ ਧਿਆਨ ਹੋ ਕੇ ਸੋਚੋ ਕਿ ਸਰੀਰ ਢਿੱਲਾ ਹੋ ਰਿਹਾ ਹੈ | ਅਨੁਭਵ ਕਰੋ ਕਿ ਸਰੀਰ ਵਿਸ਼ਰਾਮ ਸਥਿਤੀ ਵਿਚ ਹੈ । ਇਹ ਆਸਣ 3 ਤੋਂ 5 ਮਿੰਟ ਕਰਨਾ ਹੈ । ਇਸ ਆਸਣ ਦਾ ਅਭਿਆਸ ਹਰੇਕ ਆਸਣ ਦੇ ਸ਼ੁਰੂ ਵਿਚ ਅਤੇ ਅੰਤ ਵਿਚ ਕਰਨਾ ਜ਼ਰੂਰੀ ਹੈ ।

ਮਹੱਤਵ (Importance) –

1. ਸ਼ਵ ਆਸਣ ਨਾਲ ਉੱਚ ਰਕਤ ਚਾਪ ਅਤੇ ਮਾਨਸਿਕ ਤਣਾਓ ਤੋਂ ਛੁਟਕਾਰਾ ਮਿਲਦਾ ਹੈ ।
2. ਇਹ ਦਿਲ ਅਤੇ ਦਿਮਾਗ ਨੂੰ ਤਾਜ਼ਾ ਰੱਖਦਾ ਹੈ ।
3. ਇਸ ਆਸਣ ਦੁਆਰਾ ਸਰੀਰ ਦੀ ਥਕਾਵਟ ਦੂਰ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਅਸ਼ਟਾਂਗ ਯੋਗ ਦੇ ਅੰਗਾਂ ਬਾਰੇ ਵਿਸਥਾਰ ਪੂਰਵਕ ਲਿਖੋ । (Write in detail about the parts of Astanga Yoga.)
ਉੱਤਰ-
ਅਸ਼ਟਾਂਗ ਯੋਗ
(Ashtang Yoga)
ਅਸ਼ਟਾਂਗ ਯੋਗ ਦੇ ਅੱਠ ਅੰਗ ਹਨ, ਇਸੇ ਕਰਕੇ ਇਸ ਦਾ ਨਾਂ ਅਸ਼ਟਾਂਗ ਯੋਗ ਹੈ ।
ਯੋਗ ਅਭਿਆਸ ਦੀਆਂ ਪਾਤੰਜਲੀ ਰਿਸ਼ੀ ਅਨੁਸਾਰ ਹੇਠ ਲਿਖੀਆਂ ਅੱਠ-ਅਵਸਥਾਵਾਂ ਮੰਨੀਆਂ ਗਈਆਂ ਹਨ-

1. ਯਮ (Yama, Forbearance)
2. ਨਿਯਮ (Niyama, Observance)
3. ਆਸਣ (Asana, Posture)
4. ਪਾਣਾਯਾਮ (Pranayama, Regulation of breathing)
5. ਪ੍ਰਤਿਆਹਾਰ (Pratyahara, Abstraction)
6. ਧਾਰਨਾ (Dharana, Concentration)
7. ਧਿਆਨ (Dhyana, Meditation)
8. ਸਮਾਧੀ (Samadhi, Trance)

ਯੋਗ ਦੀਆਂ ਇਹਨਾਂ ਉੱਪਰ ਵਰਣਿਤ ਅੱਠ ਅਵਸਥਾਵਾਂ ਵਿਚੋਂ ਪਹਿਲੀਆਂ ਪੰਜ ਅਵਸਥਾਵਾਂ ਦਾ ਸੰਬੰਧ ਬਾਹਰਲੀਆਂ ਯੋਗਿਕ-ਕਿਰਿਆਵਾਂ ਨਾਲ ਹੈ । ਬਾਕੀ ਦੀਆਂ ਤਿੰਨ ਅਵਸਥਾਵਾਂ ਦਾ ਸੰਬੰਧ ਅੰਦਰੁਨੀ ਯੋਗਿਕ-ਕਿਰਿਆਵਾਂ ਨਾਲ ਹੈ । ਇਹ ਸਾਰੀਆਂ ਅਵਸਥਾਵਾਂ ਹੇਠਾਂ ਵੰਡੀਆਂ ਹੋਈਆਂ ਹਨ ਜਿਵੇਂ-
1. ਯਮ (Yama, Forbearance) – ਯਮ ਦੇ ਹੇਠ ਦਿੱਤੇ ਪੰਜ ਅੰਗ ਹਨ-

• ਅਹਿੰਸਾ (Ahimsa, Non-Violence)
• ਸਤਿਅ (Satya, Truth)
• ਅਸਤੇਯ (Asteya, Conquest of the senses of mind)
• ਅਪ੍ਰੀਹਿ (Aprigrahha, Non-receiving)
• ਬ੍ਰਹਮਚਰੀਆ (Brahamcharaya, Celibacy)

2. ਨਿਯਮ (Niyama, Observance) – ਇਸ ਦੇ ਪੰਜ ਅੰਗ ਹਨ-

• ਤਪ (Tapa, Penance)
• ਸਵਾਧਿਆਏ (Swadhyay, Self-study)
• ਈਸ਼ਵਰ ਪਧਾਨ (Iswar Pridhan, God Consciousness)
• ਸੋਚ
• ਸੰਤੋਸ਼ ।

3. ਆਸਣ (Asana, Posture) – ਆਸਣਾਂ ਦੀ ਸੰਖਿਆ ਜਿੰਨੇ ਪਸ਼ੂ-ਪੰਛੀ ਹਨ, ਓਨੀ ਹੈ । ਆਸਣ ਸਰੀਰਕ ਸਮਰੱਥਾ, ਸ਼ਕਤੀ ਦੇ ਅਨੁਸਾਰ, ਨਿੱਤ-ਪ੍ਰਤੀ ਹਵਾ ਦੇ ਬਾਹਰ ਕੱਢਣ, ਸਾਹ ਰੋਕਣ ਅਤੇ ਫਿਰ ਸਾਹ ਲੈਣ ਦੇ ਨਾਲ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ ।

4. ਪ੍ਰਾਣਾਯਾਮ (Pranayama, Regulation of breathing) – ਪ੍ਰਾਣਾਯਾਮ ਉਪਾਸ਼ਨਾ ਦਾ ਭਾਰਾ ਹੈ । ਇਸ ਦੇ ਤਿੰਨ ਹਿੱਸੇ ਹਨ-

• ਪੂਰਕ (Purak, Inhalation)
• ਰੇਚਕ (Rechak, Exhalation).
• ਕੁੰਭਕ (Kumbhak, Holding of Breath) – ਕਈ ਆਸਣ ਲਗਾ ਕੇ ਸਾਹ ਲੈ ਕੇ ਫਿਰ ਰੋਕ ਕੇ ਬਾਹਰ ਕੱਢਣ ਨੂੰ ਪ੍ਰਾਣਾਯਮ ਕਹਿੰਦੇ ਹਨ ।

5. ਪ੍ਰਤਿਆਹਾਰ (Pratyahara, Abstraction- ਤਿਆਹਾਰ ਤੋਂ ਭਾਵ ਵਾਪਸ ਲਿਆਉਣਾ ਅਤੇ ਦੁਨਿਆਵੀ ਖ਼ੁਸ਼ੀਆਂ ਤੋਂ ਆਪਣੇ ਮਨ ਨੂੰ ਮੋੜਨਾ ਹੈ ।

6. ਧਾਰਨਾ (Dharma, Concentration) – ਆਪਣੀਆਂ ਇੰਦਰੀਆਂ ਨੂੰ ਕਾਬੂ ਵਿਚ ਰੱਖਣ ਨੂੰ ਧਾਰਨਾ ਆਖਦੇ ਹਨ ਜੋ ਕਿ ਬਹੁਤ ਹੀ ਮੁਸ਼ਕਿਲ ਹੈ ।

7. ਧਿਆਨ (Dhyana, Meditation) – ਜਦੋਂ ਮਨ ਕਾਬੂ ਹੋ ਜਾਂਦਾ ਹੈ ਤਾਂ ਧਿਆਨ ਲੱਗਣਾ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਅਵਸਥਾ ਵਿਚ ਮਨ ਅਤੇ ਸਰੀਰ ਵਗਦੀ ਨਦੀ ਵਾਂਗ ਹੋ ਜਾਂਦੇ ਹਨ ਜਿਸ ਵਿਚ ਪਾਣੀ ਦੀ ਲਹਿਰ ਦਾ ਕੋਈ ਅਸਰ ਨਹੀਂ ਹੁੰਦਾ ।

8. ਸਮਾਧੀ (Smadhi, Trance) – ਜਿਹੜੀ ਚਿੱਤ ਦੀ ਅਵਸਥਾ ਧਾਰਨਾ ਤੋਂ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਉਹ ਸਮਾਧੀ ਵਿਚ ਖਤਮ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਸਾਰੀਆਂ ਅਵਸਥਾਵਾਂ ਦਾ ਡੂੰਘਾ ਸੰਬੰਧ ਹੈ । ਯੋਗ ਵਿਗਿਆਨ ਦੁਨੀਆਂ ਨੂੰ ਭਾਰਤ ਦੀ ਇੱਕ ਵੱਡੀ ਦੇਣ ਹੈ। ਅੱਜ-ਕਲ ਇਹ ਦੇਸ਼ ਵਿਦੇਸ਼ ਵਿਚ ਹਰਮਨ ਪਿਆਰਾ ਹੋਇਆ ਹੈ । ਇਸ ਦੀ ਉਪਯੋਗਤਾ ਦਾ ਸਿੱਕਾ ਸਾਰੇ ਡਾਕਟਰ ਅਤੇ ਸਰੀਰਕ ਅਧਿਆਪਕ ਮੰਨਦੇ ਹਨ । ਯੋਗ-ਆਸਣ ਕਸਰਤ ਵਿਧੀ ਰੂਪ ਨਾਲ ਵਿਗਿਆਨਿਕ ਅਤੇ ਸਰੀਰਕ ਬਣਤਰ ਦੇ ਅਨੁਕੂਲ ਹੈ ।

ਆਸਣ
1. ਪਦਮ ਆਸਣ ਦੀ ਵਿਧੀ (Technique of Padam asana) – ਚੌਕੜੀ ਮਾਰ ਕੇ ਬੈਠਣ ਤੋਂ ਬਾਅਦ ਪੈਰ ਖੱਬੇ ਪੱਟ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖੋ ਕਿ ਸੱਜੇ ਪੈਰ ਦੀ ਅੱਡੀ ਖੱਬੇ ਪੱਟ ਦੀ ਪੇਡ ਹੱਡੀ ਨੂੰ ਛੁਹੇ । ਇਸ ਤੋਂ ਬਾਅਦ ਖੱਬੇ ਪੈਰ ਨੂੰ ਚੁੱਕ ਕੇ ਉਸੇ ਤਰ੍ਹਾਂ ਸੱਜੇ ਪੈਰ ਦੇ ਪੱਟ ਤੇ ਰੱਖੋ ।

ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਬਿਲਕੁਲ ਸਿੱਧੀ ਰਹਿਣੀ ਚਾਹੀਦੀ ਹੈ। ਬਾਹਵਾਂ ਨੂੰ ਤਾਣ ਕੇ ਹੱਥਾਂ ਨੂੰ ਗੋਡਿਆਂ ‘ਤੇ ਰੱਖੋ | ਕੁਝ ਦਿਨਾਂ ਦੇ ਅਭਿਆਸ ਦੁਆਰਾ ਇਸ ਆਸਣ ਨੂੰ ਬਹੁਤ ਹੀ ਆਸਾਨੀ ਨਾਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।

ਲਾਭ (Advantages) –

• ਇਸ ਆਸਣ ਨਾਲ ਪਾਚਨ ਸ਼ਕਤੀ ਵਧਦੀ ਹੈ ।
• ਇਹ ਆਸਣ ਮਨ ਦੀ ਇਕਾਗਰਤਾ ਲਈ ਸਭ ਤੋਂ ਉੱਤਮ ਹੈ ।
• ਕਮਰ ਦਰਦ ਦੂਰ ਹੁੰਦਾ ਹੈ |
• ਦਿਲ ਅਤੇ ਪੇਟ ਦੇ ਰੋਗ ਨਹੀਂ ਲੱਗਦੇ |
• ਮੂਤਰ ਰੋਗਾਂ ਨੂੰ ਦੂਰ ਕਰਦਾ ਹੈ ।

2. ਵੱਜਰ ਆਸਣ (Vajur Asana)-
ਸਥਿਤੀ (Position)- ਪੈਰਾਂ ਨੂੰ ਪਿੱਛੇ ਵਲ ਕਰ ਕੇ ਬੈਠਣਾ ਅਤੇ ਹੱਥਾਂ ਨੂੰ ਗੋਡਿਆਂ ਤੇ ਰੱਖਣਾ ਇਸ ਆਸਣ ਦੀ ਸਥਿਤੀ ਹੈ ।
ਵਿਧੀ (Technique) –

• ਗੋਡੇ ਉਲਟੇ ਕਰ ਕੇ ਪੈਰ ਪਿੱਛੇ ਨੂੰ ਕਰਕੇ ਪੈਰਾਂ ਦੀਆਂ ਤਲੀਆਂ ਦੇ ਭਾਰ ਬੈਠ ਜਾਓ ।
• ਹੇਠਾਂ ਪੈਰਾਂ ਦੇ ਅੰਗੂਠੇ ਇਕ ਦੂਜੇ ਵਲ ਹੋਣ ।
• ਦੋਵੇਂ ਗੋਡੇ ਮਿਲੇ ਹੋਣ ਤੇ ਕਮਰ ਤੇ ਪਿੱਠ ਇਕ-ਦਮ ਸਿੱਧੀਆਂ ਹੋਣ ।
• ਦੋਵੇਂ ਹੱਥ ਦੱਬ ਕੇ ਗੋਡਿਆਂ ਕੋਲ ਰੱਖੋ ।
• ਸਾਹ ਦੀ ਗਤੀ ਲੰਮੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
• ਇਹ ਆਸਣ ਹਰ ਰੋਜ਼ 3 ਮਿੰਟ ਤੋਂ ਲੈ ਕੇ 20 ਮਿੰਟ ਤੱਕ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਲਾਭ (Advantages) –

• ਸਰੀਰ ਵਿਚ ਚੁਸਤੀ ਆਉਂਦੀ ਹੈ ।
• ਸਰੀਰ ਦਾ ਮੋਟਾਪਾ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਸਰੀਰ ਤੰਦਰੁਸਤ ਰਹਿੰਦਾ ਹੈ ।
• ਮਾਸ-ਪੇਸ਼ੀਆਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ।
• ਇਸ ਨਾਲ ਸੁਪਨ-ਦੋਸ਼ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਪੈਰਾਂ ਦਾ ਦਰਦ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਮਾਨਸਿਕ ਤੌਰ ਤੇ ਸ਼ਾਂਤੀ ਮਿਲਦੀ ਹੈ ।
• ਇਨਸਾਨ ਬੇ-ਫਿਕਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਇਸ ਆਸਨ ਦੁਆਰਾ ਸ਼ੂਗਰ ਦਾ ਰੋਗ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਪਾਚਨ ਸ਼ਕਤੀ ਠੀਕ ਰਹਿੰਦੀ ਹੈ ।

3. ਸ਼ਵ ਆਸਣ (Shavasana) – ਸ਼ਵ ਆਸਣ ਵਿਚ ਪਿੱਠ ਦੇ ਬਲ ਸਿੱਧਾ ਲੇਟ ਕੇ ਸਰੀਰ ਨੂੰ ਢਿੱਲਾ ਛੱਡ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਸ਼ਵ ਆਸਣ ਕਰਨ ਲਈ ਜ਼ਮੀਨ ਤੇ ਪਿੱਠ ਦੇ ਬਲ ਲੇਟ ਜਾਓ ਅਤੇ ਸਰੀਰ ਨੂੰ ਬਿਲਕੁਲ ਢਿੱਲਾ ਛੱਡ ਦਿਓ । ਹੌਲੀਹੌਲੀ ਲੰਬੇ-ਲੰਬੇ ਸਾਹ ਲਵੋ । ਬਿਲਕੁਲ ਚਿੱਤ ਲੇਟ ਕੇ ਸਾਰੇ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਨੂੰ ਬਹੁਤ ਢਿੱਲਾ ਛੱਡ ਦਿਓ । ਦੋਹਾਂ ਪੈਰਾਂ ਵਿਚ ਡੇਢ ਫੁੱਟ ਦੀ ਦੂਰੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਹੱਥਾਂ ਦੀਆਂ ਹਥੇਲੀਆਂ ਆਕਾਸ਼ ਵੱਲ ਕਰਕੇ ਸਰੀਰ ਤੋਂ ਦੂਰ ਰੱਖੋ | ਅੱਖਾਂ ਬੰਦ ਕਰਕੇ ਅੰਤਰ ਧਿਆਨ ਹੋ ਕੇ ਸੋਚੋ ਕਿ ਸਰੀਰ ਢਿੱਲਾ ਹੋ ਰਿਹਾ ਹੈ | ਅਨੁਭਵ ਕਰੋ ਕਿ ਸਰੀਰ ਵਿਸ਼ਰਾਮ ਸਥਿਤੀ ਵਿਚ ਹੈ । ਇਹ ਆਸਣ 3 ਤੋਂ 5 ਮਿੰਟ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਆਸਣ ਦਾ ਅਭਿਆਸ ਹਰੇਕ ਆਸਣ ਦੇ ਸ਼ੁਰੂ ਅਤੇ ਅੰਤ ਵਿਚ ਕਰਨਾ ਜ਼ਰੂਰੀ ਹੈ ।

ਮਹੱਤਵ (Importance) –

• ਸ਼ਵ ਆਸਣ ਨਾਲ ਉੱਚ ਰਕਤ ਚਾਪ ਅਤੇ ਮਾਨਸਿਕ ਤਣਾਓ ਤੋਂ ਛੁਟਕਾਰਾ ਮਿਲਦਾ ਹੈ ।
• ਇਹ ਦਿਲ ਅਤੇ ਦਿਮਾਗ ਨੂੰ ਤਾਜ਼ਾ ਰੱਖਦਾ ਹੈ ।
• ਇਸ ਆਸਣ ਦੁਆਰਾ ਸਰੀਰ ਦੀ ਥਕਾਵਟ ਦੂਰ ਹੁੰਦੀ ਹੈ ।

4. ਪਰਬਤ ਆਸਣ :-
ਇਸ ਨੂੰ Mountain ਆਸਣ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਚ ਸਰੀਰ ਇੱਕ ਪਰਬਤ ਦੀ ਤਰ੍ਹਾਂ ਹੁੰਦਾ ਹੈ । ਭਾਵ ਥੱਲੇ ਤੋਂ ਸਰੀਰ ਫੈਲਿਆ ਹੋਇਆ ਅਤੇ ਉੱਪਰ ਨੂੰ ਘੱਟਦਾ ਜਾਂਦਾ ਹੈ ।

ਵਿਧੀ (Technique)

• ਪਦਮ ਜਾਂ ਸੁੱਖ ਆਸਣ ਵਿਚ ਪਿੱਠ ਸਿੱਧੀ ਰੱਖਦੇ ਹੋਏ ਬੈਠ ਜਾਓ ।
• ਅੱਖਾਂ ਬੰਦ ਕਰਕੇ ਸਾਹ ਅੰਦਰ ਖਿੱਚਦੇ ਹੋਏ ਦੋਨੋਂ ਹੱਥ ਉੱਪਰ ਸਿਰ ਵੱਲ ਲੈ ਜਾਓ ।
• ਦੋਨੇਂ ਹਥੇਲੀਆ ਨੂੰ ਉੱਪਰ ਹੀ ਨਮਸਕਾਰ ਦੀ ਮੁਦਰਾ ਵਿਚ ਜੋੜ ਲਵੋ ।
• ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਅੰਦਰ ਖਿੱਚਦੇ ਅਤੇ ਛੱਡਦੇ ਰਹੋ ।
• ਫਿਰ ਸਾਹ ਛੱਡਦੇ ਹੋਏ ਬਾਹਾਂ ਥੱਲੇ ਵੱਲ ਲੈ ਆਓ ।
• ਇਸ ਵਿਧੀ ਨੂੰ ਚਾਰ ਪੰਜ ਵਾਰ ਦੁਹਰਾਓ ।

ਲਾਭ (Advantages)-

• ਪਿੱਠ, ਮੋਢੇ ਅਤੇ ਕਮਰ ਦਰਦ ਨੂੰ ਦੂਰ ਕਰਨ ਵਿਚ ਇਹ ਆਸਣ ਲਾਭਦਾਇਕ ਹੁੰਦਾ ਹੈ ।
• ਲੱਤਾਂ ਅਤੇ ਪੱਟਾਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦਾ ਹੈ ।
• ਪਾਚਨ ਪ੍ਰਣਾਲੀ ਠੀਕ ਰਹਿੰਦੀ ਹੈ ।
• ਲੰਮੇ-ਲੰਮੇ ਸਾਹ ਲੈਣ ਦੀ ਕਿਰਿਆ ਦੇ ਨਾਲ ਇਹ ਆਸਣ ਫੇਫੜਿਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦਾ ਹੈ । ਜਿਸ ਨਾਲ ਸਾਡੀਆਂ ਸਾਹ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਵੀ ਠੀਕ ਹੁੰਦੀਆਂ ਹਨ ।
• ਪਿੱਠ ਅਤੇ ਕਮਰ ਦੀ ਵਾਧੂ ਚਰਬੀ ਘਟਾਉਣ ਵਿਚ ਵੀ ਸਹਾਈ ਹੁੰਦਾ ਹੈ ।
• ਮਾਨਸਿਕ ਤਣਾਅ ਨੂੰ ਵੀ ਦੂਰ ਕਰਦਾ ਹੈ ।

5. ਪਵਨਮੁਕਤ ਆਸਣ| ਸੰਸਕ੍ਰਿਤ ਭਾਸ਼ਾ ਵਿਚ ਪਵਨ ਦਾ ਅਰਥ ਹੈ ‘ਹਵਾ’ ਅਤੇ ਮੁਕਤ ਦਾ ਅਰਥ ਹੈ ‘ਆਜ਼ਾਦੀ’ । ਇਸ ਲਈ ਇਸ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਸਰੀਰ ਦੀਆਂ ਪ੍ਰਣਾਲੀਆਂ ਵਿਚੋਂ ਵਾਧੂ ਭਰੀ ਹਵਾ ਨੂੰ ਬਾਹਰ ਕੱਢਣਾ । ਇਸ ਆਸਣ ਨੂੰ ‘Wind relieving posture’ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਾਣਾਯਾਮ (Pranayama)
ਪਰਿਭਾਸ਼ਾ (Definition) – ਪ੍ਰਾਣਾਯਾਮ ਦੋ ਸ਼ਬਦਾਂ ਤੋਂ ਬਣਿਆ ਹੈ । ‘ਪਰਾਣ’ ਦਾ ਅਰਥ ਜੀਵਨ ਅਤੇ ‘ਯਾਮ’ ਤੋਂ ਕੰਟਰੋਲ ਹੈ ਜਿਸ ਦਾ ਭਾਵ ਹੈ ਜੀਵਨ ਦਾ ਕੰਟਰੋਲ ਜਾਂ ਸਾਹ ਦਾ ਕੰਟਰੋਲ | ਪ੍ਰਾਣਾਯਾਮ ਉਹ ਕਿਰਿਆ ਹੈ ਜਿਸ ਨਾਲ ਜੀਵਨ ਦੀ ਤਾਕਤ ਨੂੰ ਵਧਾਇਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਉਸ ਤੇ ਕਾਬੂ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।
ਮਨੂ-ਮਹਾਰਾਜ ਨੇ ਕਿਹਾ, “ਪ੍ਰਾਣਾਯਾਮ ਨਾਲ ਮਨੁੱਖ ਦੇ ਸਾਰੇ ਦੋਸ਼ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਘਾਟਾਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ |’

ਪ੍ਰਾਣਾਯਾਮ ਦੀ ਨੀਂਹ (Basis of Pranayama) – ਸਾਹ ਨੂੰ ਬਾਹਰ ਕੱਢਣਾ, ਫੇਰ ਅੰਦਰ ਕਰਨਾ ਅਤੇ ਅੰਦਰ ਹੀ ਰੋਕ ਕੇ ਫੇਰ ਕੁਝ ਸਮੇਂ ਮਗਰੋਂ ਬਾਹਰ ਕੱਢਣ ਦੀਆਂ ਇਹ ਤਿੰਨੋਂ ਕਿਰਿਆਵਾਂ ਪ੍ਰਾਣਾਯਾਮ ਦੀ ਨੀਂਹ ਹਨ ।

ਸਾਹ ਬਾਹਰ ਕੱਢਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਰੇਚਕ ਕਹਿੰਦੇ ਹਨ । ਸਾਹ ਜਦੋਂ ਅੰਦਰ ਖਿੱਚਦੇ ਹਾਂ ਤਾਂ ਇਸ ਨੂੰ ਪੂਰਕ ਕਹਿੰਦੇ ਹਨ । ਸਾਹ ਨੂੰ ਅੰਦਰ ਖਿੱਚਣ ਮਗਰੋਂ ਉੱਥੇ ਹੀ ਰੋਕਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਕੁੰਭਕ ਕਹਿੰਦੇ ਹਨ । ਪ੍ਰਾਣ ਦੇ ਨਾਂ (Names of Prana) – ਵਿਅਕਤੀ ਦੇ ਸਾਰੇ ਸਰੀਰ ਵਿਚ ਪ੍ਰਾਣ ਸਮਾਇਆ ਹੈ । ਇਸ ਦੇ ਪੰਜ ਨਾਂ ਹਨ-

• ਪ੍ਰਾਣ – ਇਹ ਗਲੇ ਤੋਂ ਦਿਲ ਤਕ ਹੈ । ਇਸੇ ਪ੍ਰਾਣ ਦੀ ਤਾਕਤ ਨਾਲ ਸਾਹ ਸਰੀਰ ਵਿਚ ਹੇਠਾਂ ਨੂੰ ਜਾਂਦਾ ਹੈ ।
• ਅਪਾਣ – ਧੁੰਨੀ ਤੋਂ ਨਿਚਲੇ ਹਿੱਸੇ ਵਿਚ ਪ੍ਰਾਣ ਨੂੰ ਅਪਾਣ ਕਹਿੰਦੇ ਹਨ । ਛੋਟੀਆਂ ਅਤੇ ਵੱਡੀਆਂ ਅੰਤੜੀਆਂ ਵਿਚ ਇਹੋ ਪ੍ਰਾਣ ਹੁੰਦਾ ਹੈ । ਇਹ ਟੱਟੀ, ਪਿਸ਼ਾਬ ਅਤੇ ਹਵਾ ਨੂੰ ਸਰੀਰ ਵਿਚੋਂ ਕੱਢਣ ਲਈ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।
• ਸਮਾਣ – ਦਿਲ ਅਤੇ ਧੁਨੀ ਤਕ ਰਹਿਣ ਵਾਲੇ ਪਾਣ ਕਿਰਿਆ ਨੂੰ ਸਮਾਣ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਪਾਣ ਪਾਚਨ ਕਿਰਿਆ ਅਤੇ ਐਡਰੀਨਲ ਗਿਲਟੀ ਦੀ ਕੰਮ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਵਧਾਉਂਦਾ ਹੈ ।
• ਉਦਾਣਗਲੇ ਤੋਂ ਸਿਰ ਤਕ ਰਹਿਣ ਵਾਲੇ ਪ੍ਰਾਣ ਨੂੰ ਉਦਾਣ ਕਹਿੰਦੇ ਹਨ । ਅੱਖਾਂ, ਕੰਨ, ਨੱਕ, ਦਿਮਾਗ਼ ਆਦਿ ਅੰਗਾਂ ਦਾ ਕੰਮ ਇਸੇ ਪ੍ਰਾਣ ਕਰਕੇ ਹੁੰਦਾ ਹੈ ।
• ਧਿਆਨ – ਇਹ ਪਰਾਣ ਸਰੀਰ ਦੇ ਸਾਰੇ ਹਿੱਸੇ ਵਿਚ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਸਰੀਰ ਦੇ ਦੂਸਰੇ ਪ੍ਰਾਣਾਂ ਨਾਲ ਮੇਲ ਕਰਦਾ ਹੈ |

ਸਰੀਰ ਦੇ ਹਿੱਲਣ-ਜੁਲਣ ਤੇ ਇਸੇ ਦਾ ਕੰਟਰੋਲ ਹੁੰਦਾ ਹੈ । ਪ੍ਰਾਣਾਯਾਮ ਕਰਨ ਦੀ ਵਿਧੀ (Technique of doing Pranayama) – ਪ੍ਰਾਣਾਯਾਮ ਸਵਾਸਾਂ ਨੂੰ ਕੰਟਰੋਲ ਕਰਨ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਕਿਰਿਆ ਨਾਲ ਸਵਾਸ ਅੰਦਰ ਵੱਲ ਖਿੱਚ ਕੇ ਰੋਕ ਲਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਕੁੱਝ ਸਮਾਂ ਰੋਕਣ ਪਿੱਛੋਂ ਫਿਰ ਸਾਹ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਾਹ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਕੰਟਰੋਲ ਕਰਨ ਦਾ ਸਮਾਂ ਵਧਾਇਆ ਜਾਂਦਾ ਹੈ । ਆਪਣੀ ਸੱਜੀ ਨੱਕ ਨੂੰ ਬੰਦ ਕਰਕੇ ਖੱਬੀ ਤੋਂ ਅੱਠ ਤਕ ਗਿਣਦੇ ਹੋਏ ਸਾਹ ਖਿੱਚੋ । ਫਿਰ ਤੋਂ ਇੱਕ ਤੋਂ ਦਸ ਤਕ ਗਿਣਦੇ ਸਾਹ ਰੋਕ ਛੱਡੋ । ਉਸ ਤੋਂ ਮਗਰੋਂ ਖੱਬੀ ਨੱਕ ਬੰਦ ਕਰਕੇ ਸੱਜੀ ਤੋਂ ਅੱਠ ਗਿਣਦੇ ਹੋਏ ਸਾਹ ਛੱਡੋ ਅਤੇ ਫਿਰ ਇੱਕ ਤੋਂ ਦਸ ਤਕ ਗਿਣ ਕੇ ਇਸ ਤਰ੍ਹਾਂ ਪੂਰਾ ਸਾਹ ਨਿਕਲ ਜਾਵੇਗਾ । ਹੁਣ ਫੇਰ ਉਸੇ ਤਰ੍ਹਾਂ ਸੱਜੀ ਨੱਕ ਤੋਂ ਗਿਣਦੇ ਹੋਏ ਸਾਹ ਖਿੱਚੋ । ਇੱਕ ਤੋਂ ਦਾ ਤਕ ਗਿਣ ਕੇ ਉਸ ਨੂੰ ਰੋਕ ਦਿਓ । ਇਸ ਤਰ੍ਹਾਂ ਪੁਰਾ ਸਾਹ ਨਿਕਲ ਜਾਵੇਗਾ । ਹੁਣ ਫੇਰ ਉਸੇ ਤਰ੍ਹਾਂ ਸੱਜੀ ਨੱਕ ਤੋਂ ਗਿਣ ਹੋਏ ਸਾਹ ਖਿੱਚੋ । ਨੌਂ-ਦਸ ਤਕ ਰੋਕੋ । ਫਿਰ ਸੱਜੀ ਨੱਕ ਬੰਦ ਕਰਕੇ ਖੱਬੀ ਤੋਂ ਅੱਠ ਤਕ ਗਿਣਦੇ ਹੋਏ ਬਾਹਰ ਕੱਢ ਦਿ ਅਤੇ ਨੌਂ-ਦਸ ਤਕ ਰੋਕੋ ।

ਪ੍ਰਾਣਾਯਾਮ ਦੇ ਭੇਦ (Kinds of Pranayana) – ਸ਼ਾਸਤਰਾਂ ਵਿਚ ਪ੍ਰਾਣਾਯਾਮ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਦਿੱਤੇ ਹੋਏ ਹਨ ਪਰ ਆਮ ਇਹ ਅੱਠ ਹੁੰਦੇ ਹਨ-

(i) ਸੂਰਜ ਭੇਦੀ ਪ੍ਰਾਣਾਯਾਮ
(ii) ਉਜਈ ਪ੍ਰਾਣਾਯਾਮ
(iii) ਸ਼ੀਤਕਾਰੀ ਪ੍ਰਾਣਾਯਾਮ
(iv) ਸ਼ੀਤਲੀ ਪ੍ਰਾਣਾਯਾਮ
(v) ਭਸਤਰਕਾ ਪਾਣਾਯਾਮ
(vi) ਭਰਮਰੀ ਪ੍ਰਾਣਾਯਾਮ
(vii) ਮੂਰਛਾ ਪ੍ਰਾਣਾਯਾਮ
(viii) ਕਪਾਲਭਾਤੀ ਪ੍ਰਾਣਾਯਾਮ

ਇਨ੍ਹਾਂ ਅੱਠਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਹੇਠਾਂ ਕੀਤਾ ਗਿਆ ਹੈ-
(i) ਸੂਰਜ ਭੇਦੀ ਪ੍ਰਾਣਾਯਾਮ – ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਤਾਕਤ ਇਸ ਨਾਲ ਵਧਦੀ ਹੈ । ਇੱਛਾ ਸ਼ਕਤੀ ਵਧਦੀ ਹੈ । ਇਸਨੂੰ ਪਦਮ ਆਸਮ ਲਗਾ ਕੇ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਪਿੱਠ, ਗਰਦਨ, ਛਾਤੀ ਅਤੇ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਸਿੱਧੀ ਰੱਖਣੀ ਚਾਹੀਦੀ ਹੈ | ਖੱਬੇ ਹੱਥ ਦੀ ਉਂਗਲ ਦੇ ਨਾਲ ਨੱਕ ਦਾ ਖੱਬਾ ਛੇਕ ਬੰਦ ਕਰ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਸੱਜੇ ਛੇਕ ਤੋਂ ਸਾਹ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਸਾਹ ਅੰਦਰ ਖਿੱਚ ਕੇ ਕੁੰਭਕ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਜਦੋਂ ਤਕ ਸਾਹ ਰੋਕਿਆ ਜਾ ਸਕੇ ਰੋਕਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਤੋਂ ਮਗਰੋਂ ਅੰਗੂਠੇ ਨਾਲ ਸੱਜੇ ਛੇਕ ਨੂੰ ਦਬਾ ਕੇ ਖੱਬੇ ਛੇਕ ਤੋਂ ਆਵਾਜ਼ ਕਰਦੇ ਹੋਏ ਸਾਹ ਨੂੰ ਬਾਹਰ ਕੱਢਿਆ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ । ਪਹਿਲਾਂ ਤਿੰਨ ਵਾਰ ਅਭਿਆਸ ਹੋਣ ਤੇ ਪੰਦਰਾਂ ਵਾਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
ਇਸ ਵਿਚ ਸਾਹ ਹੋਲੀ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ । ਕੁੰਭਕ ਯਾਨੀ ਸਾਹ ਰੋਕਣ ਦਾ ਸਮਾਂ ਵਧਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।

(ii) ਉਜਾਈ ਪ੍ਰਾਣਾਯਾਮ – ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਠੀਕ ਸਾਹ ਲੈਣ ਲਈ ਨੀਂਵ ਦਾ ਕੰਮ ਕਰਦੀ ਹੈ । ਯੋਗ ਵਿੱਚ ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਵਿਸ਼ਵਾਸ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਕਿ ਸਾਡੇ ਜੀਵਨ ਨੂੰ ਮਿਣਤੀ ਦੇ ਸਾਹ ਮਿਲੇ ਹਨ । ਇਸ ਲਈ ਸਾਹ ਨੂੰ ਠੀਕ ਰੱਖਣ ਲਈ ਜੀਵਨ ਕਾਲ ਦੇ ਵਿੱਚ ਵਾਧਾ ਕਰਨ ਲਈ ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਬੈਠਣ ਦੀ ਮੁਦਰਾ-ਪੈਰਾਂ ਨੂੰ ਕਰਾਂਸ ਕਰਕੇ ਆਰਾਮ ਨਾਲ ਬੈਠੇ ਅਤੇ ਹੌਲੀ-ਹੌਲੀ ਆਪਣੀਆਂ ਅੱਖਾਂ ਨੂੰ ਬੰਦ ਕਰੋ । ਆਪਣੇ ਸਰੀਰ ਅਤੇ ਦਿਮਾਗ਼ ਨੂੰ ਆਰਾਮ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਰੱਖੋ । ਤਕਨੀਕ-ਗਹਿਰਾਈ ਨਾਲ ਅੰਦਰ ਨੂੰ ਸਾਹ ਖਿੱਚੋ ਅਤੇ ਹੌਲੀਹੌਲੀ ਸਾਹ ਬਾਹਰ ਕੱਢੋ, ਆਪਣੀ ਗਰਦਨ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਕੇ ਸਾਹ ਲੈਂਦੇ ਸਮੇਂ ਮੂੰਹ ਵਿੱਚੋਂ ਆਵਾਜ਼ ਕੱਢੋ । ਜਦੋਂ ਫੇਫੜਿਆਂ ਵਿੱਚ ਹਵਾ ਭਰ ਜਾਵੇ, ਸਾਹ ਨੂੰ ਰੋਕ ਕੇ ਰੱਖੋ, ਸੱਜੀ ਨੱਕ ਨੂੰ ਬੰਦ ਕਰੋ ਤੇ ਹੌਲੀ-ਹੌਲੀ ਖੱਬੀ ਨੱਕ ਨਾਲ ਸਾਹ ਬਾਹਰ ਕੱਢੋ, ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਦਾ ਪਹਿਲਾਂ ਚੱਕਰ ਹੈ । ਇਸ ਨੂੰ 10-15 ਬਾਰ ਕਰੋ ।

ਸਾਵਧਾਨੀਆਂ-

1. ਪਹਿਲਾਂ-ਪਹਿਲਾਂ ਇਸ ਵਿਆਯਾਮ ਨੂੰ ਬਿਨਾਂ ਸਾਹ ਰੋਕੇ ਹੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
2. ਜਿਨ੍ਹਾਂ ਲੋਕਾਂ ਨੂੰ ਉੱਚ ਰਕਤਚਾਪ ਜਾਂ ਦਿਲ ਦੀ ਬੀਮਾਰੀ ਹੋਵੇ ਉਨ੍ਹਾਂ ਨੂੰ ਇਹ ਵਿਆਯਾਮ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।
3. ਇਹ ਵਿਆਯਾਮ ਯੋਗ ਸ਼ਿਕਸ਼ਕ ਦੀ ਦੇਖ-ਰੇਖ ਵਿੱਚ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਲਾਭ:-

1. ਜੁਕਾਮ ਨੂੰ ਠੀਕ ਕਰਦਾ ਹੈ ਅਤੇ ਗਲਾ ਸਾਫ਼ ਕਰਦਾ ਹੈ ।
2. ਸਾਹ ਕਿਰਿਆ ਨਾਲ ਮੇਲਜੋਲ ਵੱਧਦਾ ਹੈ ।
3. ਖਰਾਟਿਆਂ ਨੂੰ ਠੀਕ ਕਰਦਾ ਹੈ ।
4. ਸਰੀਰ ਦੇ ਹੇਠਲੇ ਭਾਗ ਨੂੰ ਠੀਕ ਰੱਖਦਾ ਹੈ ਤੇ ਚਾਰੋਂ ਪਾਸੇ ਮਾਸ ਨੂੰ ਘੱਟ ਕਰਦਾ ਹੈ ।
5. ਥਾਇਰਾਈਡ ਦੇ ਰੋਗੀਆਂ ਲਈ ਇਹ ਵਿਆਯਾਮ ਲਾਭਦਾਇਕ ਹੈ ।

(iii) ਸ਼ੀਤਕਾਰੀ ਪ੍ਰਾਣਾਯਾਮ – ਇਹ ਸ਼ੀਤਲੀ ਪ੍ਰਾਣਾਯਾਮ ਦਾ ਹੀ ਅੰਗ ਹੈ । ‘ਸ਼ੀਤ ਦਾ ਅਰਥ ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਆਵਾਜ਼ ਤੋਂ ਹੈ, ਜੋ ਸਾਹ ਲੈਣ ਦੇ ਦੌਰਾਨ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ‘ਕਾਰੀ’ ਦਾ ਅਰਥ, ਪੈਦਾ ਕਰਨਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸੀਤਕਾਰੀ ਪ੍ਰਾਣਾਯਾਮ ਇਸ ਤਰ੍ਹਾਂ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਸ਼ੀ ਦੀ ਆਵਾਜ਼ ਪੈਦਾ ਹੋਵੇ ।

ਬੈਠਣ ਦੀ ਮੁਦਰਾ – ਕਿਸੇ ਆਸਣ ਵਿੱਚ ਬੈਠ ਜਾਉ ਤੇ ਹੌਲੀ-ਹੌਲੀ ਅੱਖਾਂ ਨੂੰ ਬੰਦ ਕਰ ਲਉ ਸਰੀਰ ਅਤੇ ਅੱਖਾਂ ਨੂੰ ਆਰਾਮ ਦਿਉ । ਤਕਨੀਕ-ਆਪਣੇ ਉੱਪਰਲੇ ਅਤੇ ਹੇਠਲੇ ਦੰਦਾਂ ਨੂੰ ਮਿਲਾਉ, ਆਪਣੇ ਹੋਠਾਂ ਨੂੰ ਜਿੰਨਾ ਹੋ ਸਕੇ ਫੈਲਾਉ, ਆਪਣੀ ਜੀਭ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਮੋੜੋ ਕਿ ਉਸਦਾ ਉੱਪਰਲਾ ਭਾਗ ਮੁੰਹ ਦੇ ਉੱਪਰਲੇ ਭਾਗ ਨੂੰ ਛੂ ਲਵੇ ‘ਸ਼ੀ ਦੀ ਆਵਾਜ਼ ਹੌਲੀ-ਹੌਲੀ ਲੈਂਦੇ ਹੋਏ ਗਹਿਰਾ ਸਾਹ ਲਉ, ਸਾਹ ਲੈਣ ਮਗਰੋਂ ਬੁੱਲਾਂ ਨੂੰ ਬੰਦ ਕਰਕੇ ਰੱਖੋ ਅਤੇ ਜੀਭ ਨੂੰ ਆਰਾਮ ਦਿਉ । ਆਪਣੇ ਸਾਹ ਨੂੰ ਜਿੰਨਾ ਹੋ ਸਕੇ, ਰੋਕੋ ਅਤੇ ਆਪਣੇ ਨੱਕ ਦੁਆਰਾ ਸਾਹ ਨੂੰ ਬਾਹਰ ਕੱਢ ਪਰੰਤੂ ਮੂੰਹ ਨਹੀਂ ਖੁੱਲ੍ਹਣਾ ਚਾਹੀਦਾ । ਇਹ ਸ਼ੀਤਕਾਰੀ ਪ੍ਰਾਣਾਯਾਮ ਦਾ ਪਹਿਲਾਂ ਭਾਗ ਹੈ । ਇਹ 10, 15 ਸ਼ੀਤਕਾਰੀ ਪ੍ਰਾਣਾਯਾਮ ਵਾਰੀ ਦੋਹਰਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਸਾਵਧਾਨੀਆਂ-

1. ਜਿਸ ਵਿਅਕਤੀ ਨੂੰ ਜ਼ੁਕਾਮ, ਅਸਥਮਾ ਹੋਵੇ, ਉਸਨੂੰ ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।
2. ਠੰਡੇ ਮੌਸਮ ਵਿੱਚ ਇਹ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।
3. ਜਿਸ ਵਿਅਕਤੀ ਨੂੰ ਉੱਚ ਰਕਤਚਾਪ ਹੋਵੇ, ਉਸਨੂੰ ਵੀ ਇਹ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।

ਲਾਭ –

1. ਇਹ ਆਸਣ ਪਾਈਰਿਆ ਦੇ ਰੋਗ ਨੂੰ ਠੀਕ ਕਰਦਾ ਹੈ ਤੇ ਮੂੰਹ ਨੂੰ ਸਾਫ਼ ਕਰਦਾ ਹੈ । ਇਹ ਦੰਦ ਤੇ ਮਸੂੜਿਆਂ ਨੂੰ ਠੀਕ ਰੱਖਦਾ ਹੈ !
2. ਸਰੀਰ ਨੂੰ ਅਧਿਕ ਤਾਕਤ ਦਿੰਦਾ ਹੈ ।
3. ਸਰੀਰ ਅਤੇ ਦਿਮਾਗ਼ ਨੂੰ ਠੰਡਾ ਰੱਖਦਾ ਹੈ ।
4. ਤਨਾਵ ਨੂੰ ਦੂਰ ਕਰਨ ਲਈ ਬਹੁਤ ਲਾਭਦਾਇਕ ਹੈ ।

(iv) ਸ਼ੀਤਲੀ ਪ੍ਰਾਣਾਯਾਮ-ਇਹ ਹੱਠ ਯੋਗ ਦਾ ਇੱਕ ਭਾਗ ਹੈ, ਸ਼ੀਤਲ ਦਾ ਭਾਵ ਸ਼ਾਂਤ ਹੈ, ਇਹ ਇੱਕ ਸਾਹ ਕਿਰਿਆ ਦਾ ਵਿਆਯਾਮ ਹੈ, ਜੋ ਸਾਡੀ ਅੰਦਰੂਨੀ ਗਰਮੀ ਨੂੰ ਸ਼ਾਂਤ ਕਰਦਾ ਹੈ ਅਤੇ ਮਾਨਸਿਕ, ਸਰੀਰਿਕ ਤੇ ਭਾਵਾਤਮਕ ਸੰਤੁਲਨ ਨੂੰ ਕਾਇਮ ਕਰ ਸਕਦਾ ਹੈ ।

ਬੈਠਣ ਦੀ ਮੁਦਰਾ – ਪੈਰਾਂ ਨੂੰ ਕਰਾਂਸ ਕਰਕੇ ਆਰਾਮ ਨਾਲ ਜ਼ਮੀਨ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਬੈਠੋ ਕਿ ਪੈਰ ਉੱਪਰ ਨੂੰ ਜਾਣ ਅਤੇ ਪੈਰਾਂ ਦੇ ਤਲਵੇ ਵੀ ਉੱਪਰ ਹੋਣ, ਆਪਣੇ ਪੈਰਾਂ ਅਤੇ ਰੀੜ ਦੀ ਹੱਡੀ ਨੂੰ ਸਿੱਧਾ ਰੱਖਦੇ ਹੋਏ ਉਂਗਲੀ ਦੇ ਸਿਰਿਆਂ ਨੂੰ ਅੰਗੂਠੇ ਨਾਲ ਮਿਲਾਉ, ਬਾਕੀ ਦੀਆਂ ਉਂਗਲੀਆਂ ਨੂੰ ਬਰਾਬਰ ਫੈਲਾ ਕੇ ਢਿੱਲਾ ਛੱਡੋ । ਹੌਲੀ-ਹੌਲੀ ਆਪਣੀ ਅੱਖਾਂ ਨੂੰ ਬੰਦ ਕਰੋ ਤੇ ਸਰੀਰ ਅਤੇ ਦਿਮਾਗ਼ ਨੂੰ ਆਰਾਮ ਦਿਉ ।

ਤਕਨੀਕ – ਆਪਣਾ ਮੂੰਹ ਖੋਲ੍ਹੇ ਅਤੇ ਹੌਲੀ-ਹੌਲੀ ਜੀਭ ਨੂੰ ਬਾਹਰਲੀ ਤਰਫ਼ ਕੱਢ ਕੇ ਮੋੜਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੋ ਅਤੇ ਆਰਾਮ ਨਾਲ ਆਵਾਜ਼ ਕਰਦੇ ਹੋਏ ਸ਼ੀਤਲੀ ਪ੍ਰਾਣਾਯਾਮ ਸਾਹ ਲਉ, ਸਾਹ ਲੈਂਦੇ ਸਮੇਂ ਇਸ ਦੀ ਸ਼ੀਤਲਤਾ ਨੂੰ ਮਹਿਸੂਸ ਕਰੋ, ਹੁਣ ਆਪਣੀ ਜੀਭ ਨੂੰ ਅੰਦਰ ਲੈ ਜਾਉ ਜਦੋਂ ਤੱਕ ਸੰਭਵ ਹੋਵੇ ਸਾਹ ਨੂੰ ਰੋਕ ਕੇ ਰੱਖੋ । ਇਸ ਬਾਰੇ ਸੋਚੋ ਕਿ ਸਾਹ ਤੁਹਾਡੇ ਦਿਮਾਗ ਨੂੰ ਸੇਜ ਰਹੀ ਹੋਵੇ ਅਤੇ ਸਾਰੇ ਸਰੀਰ ਦੇ ਤੰਤੂਆਂ ਵਿੱਚ ਫੈਲ ਰਹੀ ਹੈ । ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਛੱਡਦੇ ਹੋਏ ਸ਼ੀਤਲਤਾ ਨੂੰ ਮਹਿਸੂਸ ਕਰੋ । ਇਹ ਸ਼ੀਤਲੀ ਪ੍ਰਾਣਾਯਾਮ ਦਾ ਪਹਿਲਾ ਚਰਨ ਹੈ । ਇਸਨੂੰ 10 ਜਾਂ 15 ਵਾਰ ਕਰੋ ।

ਸਾਵਧਾਨੀਆਂ-

1. ਜਿਨ੍ਹਾਂ ਲੋਕਾਂ ਨੂੰ ਠੰਡ, ਜ਼ੁਕਾਮ, ਅਸਥਮਾ ਜਾਂ ਆਰਥਰਾਈਟਸ ਜਾਂ ਬਰੰਕਟਾਈਟਸ ਜਾਂ ਦਿਲ ਦੀ ਬੀਮਾਰੀ ਹੋਵੇ, ਉਨ੍ਹਾਂ ਨੂੰ ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।
2. ਇਸ ਪ੍ਰਾਣਾਯਾਮ ਦਾ ਅਭਿਆਸ ਸਰਦ ਮੌਸਮ ਵਿੱਚ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।

ਲਾਭ-

1. ਇਹ ਖੂਨ ਨੂੰ ਸਾਫ਼ ਰੱਖਦਾ ਹੈ ਅਤੇ ਸਰੀਰ ਤੇ ਦਿਮਾਗ਼ ਨੂੰ ਤਰੋਤਾਜ਼ਾ ਕਰਦਾ ਹੈ ।
2. ਸਰੀਰ ਅਤੇ ਦਿਮਾਗ਼ ਨੂੰ ਸ਼ਾਂਤ ਰੱਖਦਾ ਹੈ ।
3. ਇਹ ਆਸਣ ਉਨ੍ਹਾਂ ਲੋਕਾਂ ਲਈ ਲਾਭਦਾਇਕ ਹੈ, ਜੋ ਸਾਰਾ ਦਿਨ ਸੁਸਤੀ ਅਤੇ ਥਕਾਵਟ ਮਹਿਸੂਸ ਕਰਦੇ ਹਨ ।
4. ਇਹ ਆਸਣ ਪਾਚਨ ਕਿਰਿਆ ਨੂੰ ਸੁਧਾਰਦਾ ਹੈ ਅਤੇ ਉੱਚ ਰਕਤਚਾਪ ਨੂੰ ਠੀਕ ਕਰਦਾ ਹੈ ।
5. ਇਹ ਗੁੱਸ. ਚਿੰਤਾ ਅਤੇ ਤਨਾਵ ਨੂੰ ਘੱਟ ਕਰਦਾ ਹੈ ।

(v) ਭਸਤਰਕਾ ਪਾਣਾਯਾਮ – ਇਸ ਪ੍ਰਾਣਾਯਾਮ ਵਿਚ ਲੋਹਾਰ ਦੀ ਕਣੀ ਦੀ ਤਰ੍ਹਾਂ ਸਾਹ ਅੰਦਰ ਅਤੇ ਬਾਹਰ ਲਿਆ | ਅਤੇ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ । ਪਹਿਲਾਂ ਨੱਕ ਦੀ ਇਕ ਛੇਕ ਤੋਂ ਸਾਹ ਲੈ ਕੇ ਦੁਸਰੇ ਛੇਕ ਰਾਹੀਂ ਸਾਹ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਮਗਰੋਂ ਦੂਜੇ ਛੇਕਾਂ ਤੋਂ ਸਾਹ ਬਾਹਰ ਅਤੇ ਅੰਦਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਭਸਤਰਕਾ ਪ੍ਰਾਣਾਯਾਮ ਸ਼ੁਰੂ ਵਿਚ ਹੌਲੀ ਅਤੇ ਮਗਰੋਂ ਇਸ ਦੀ ਰਫ਼ਤਾਰ ਵਧਾਈ ਜਾਂਦੀ ਹੈ । ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਕਰਨ ਨਾਲ ਮਨੁੱਖ ਦਾ ਮੋਟਾਪਾ ਘਟਦਾ ਹੈ । ਮਨ ਦੀ ਇੱਛਾ ਬਲਵਾਨ ਹੁੰਦੀ ਹੈ । ਵਿਚਾਰ ਠੀਕ ਰਹਿੰਦੇ ਹਨ ।

(vi) ਭਰਮਰੀ ਪ੍ਰਾਣਾਯਾਮ – ਕਿਸੇ ਆਸਣ ਵਿੱਚ ਬੈਠ ਕੇ ਕੂਹਣੀਆਂ ਨੂੰ ਮੇਵਿਆਂ ਬਰਾਬਰ ਕਰਕੇ ਸਾਹ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਥੋੜੀ ਦੇਰ ਸਾਹ ਰੋਕਣ ਮਗਰੋਂ ਸਾਹ ਬਾਹਰ ਕੱਢਦੇ ਸਮੇਂ ਭਰੇ ਵਰਗੀ ਆਵਾਜ਼ ਗਲੇ ਤੋਂ ਕੱਢੀ ਜਾਂਦੀ ਹੈ । ਦੋ ਸਕਿੰਟ ਸਹ ਕੱਢ ਕੇ ਬਾਹਰ ਰੋਕਿਆ ਜਾਂਦਾ ਹੈ ! ਇਸ ਤਰਾਂ ਆਵਾਜ਼ ਕਰਦੇ ਹੋਏ ਬਾਹ ਅੰਦਰ ਖਿੱਚਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਾਣਾਯਾਮ ਦਾ ਅਭਿਆਸ ਸੱਤ ਤੋਂ ਦਸ ਵਾਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਰੇਚਕ ਜਿੱਥੋਂ ਤੱਕ ਹੋ ਸਕੇ ਲੰਮਾ ਕੀਤਾ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ | ਆਵਾਜ਼ ਅਤੇ ਰੇਚਕ ਕਰਦੇ ਹੋਏ ਮੁੰਹ ਬੰਦ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਲਾਭ (Advantages)-ਇਸ ਦੇ ਅਭਿਆਸ ਨਾਲ ਆਵਾਜ਼ ਸਾਫ਼ ਅਤੇ ਮਿੱਠੀ ਹੁੰਦੀ ਹੈ । ਗਲੇ ਦੀਆਂ ਬੀਮਾਰੀਆਂ ਦੂਰ ਰਹਿੰਦੀਆਂ ਹਨ ।

(vii) ਮੂਰਛਾ (ਨਾੜੀ ਸੋਧ) ਪ੍ਰਾਣਾਯਾਮ – ਇਸ ਪ੍ਰਾਣਾਯਾਮ ਨਾਲ ਨਾੜੀਆਂ ਦੀ ਸਫ਼ਾਈ ਹੁੰਦੀ ਹੈ । ਸਿੱਧ ਆਸਣ ਵਿੱਚ ਬੈਠ ਕੇ ਨੱਕ ਦੇ ਖੱਬੇ ਪਾਸਿਉਂ ਸਾਹ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ ! ਸਾਹ ਲੈ ਕੇ ਕੁੰਭਕ ਕੀਤਾ ਜਾਵੇ । ਇਸਦੇ ਮਗਰੋਂ ਦੂਜੇ ਪਾਸੇ ਤੋਂ ਸਾਹ ਹੌਲੀ-ਹੌਲੀ ਬਾਹਰ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ । ਫੇਰ ਸੱਜੇ ਨੱਕ ਨਾਲ ਸਾਹ ਅੰਦਰ ਭਰਿਆ ਜਾਂਦਾ ਹੈ । ਕੁੱਝ ਸਮੇਂ ਲਈ ਅੰਦਰੂਨੀ ਕੁੰਭਕ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਨਾਲ ਹੀ ਖੱਬੇ ਨੱਕ ਨਾਲ ਸਾਹ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿੱਚ 1: 2: 2 ਦਾ ਅਨੁਪਾਤ ਹੋਵੇ ਜਿਵੇਂ ਕਿ ਸਾਹ ਲੈਣ ਵਿੱਚ ਚਾਰ ਸੈਕਿੰਡ, ਸਾਹ ਰੋਕਣ ਵਿੱਚ ਦਸ ਮੋਕਿੰਡ, ਸਾਹ ਕੱਢਣ ਲਈ ਦਸ ਸੈਕਿੰਡ । ਹੌਲੀ-ਹੌਲੀ ਕੁੰਭਕ ਨੂੰ ਵਧਾਇਆ ਜਾ ਸਕਦਾ ਹੈ । ਕੁੰਭਕ ਨਾਲ ਆਕਸੀਜਨ ਫੇਫੜਿਆਂ ਦੇ ਸਾਰੇ ਛੇਕਾਂ ਵਿੱਚ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ । ਰੇਚਕ ਨਾਲ ਫੇਫੜੇ ਸੁੰਗੜ ਜਾਂਦੇ ਹਨ ਅਤੇ ਹਵਾ ਬਾਹਰ ਨਿਕਲ ਜਾਂਦੀ ਹੈ । ਲਾਭ (Advantages)-ਇਸ ਪ੍ਰਾਣਾਯਾਮ ਨਾਲ ਫੇਫੜਿਆਂ ਦੀਆਂ ਬੀਮਾਰੀਆਂ ਅਤੇ ਦਿਲ ਦੀ ਕਮਜ਼ੋਰੀ ਨੂੰ ਲਾਭ ਪਹੁੰਚਦਾ ਹੈ ।

(viii) ਕਪਾਲਭਾਤੀ ਪ੍ਰਾਣਾਯਾਮ – ਕਪਾਲਭਾਤੀ ਸ਼ਬਦ ਸੰਸਕ੍ਰਿਤ ਦਾ ਹੈ । ਕਪਾਲ ਦਾ ਅਰਥ ‘ਲਲਾਟ’ ਹੈ ਅਤੇ ‘ਭਾਤੀ ਦਾ ਅਰਥ ਹੈ ਚਮਕਣਾ । ਇਸ ਤਰ੍ਹਾਂ ਕਪਾਲਭਾਤੀ ਦਾ ਮਤਲਬ ਅੰਦਰੂਨੀ ਭਾਂਤੀ ਦੇ ਨਾਲ ਚੇਹਰੇ ਦਾ ਚਮਕਣਾ ਹੈ । ਇਹ ਇੱਕ ਜ਼ਿਆਦਾ ਸ਼ਕਤੀ ਦੇਣ ਵਾਲਾ ਪੇਟ ਦਾ ਵਿਆਯਾਮ ਹੈ । ਇਸ ਵਿੱਚ ਤੇਜ਼ੀ ਨਾਲ ਸਾਹ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਆਰਾਮ ਨਾਲ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਬੈਠਣ ਦੀ ਮੁਦਰਾ-ਪਿੱਠ ਨੂੰ ਸਿੱਧਾ ਰੱਖਦੇ ਹੋਏ ਪੈਰਾਂ ਨੂੰ ਕਰਾਂਸ ਕਰਕੇ ਬੈਠੋ ਅਤੇ ਆਪਣੇ ਹੱਥਾਂ ਨੂੰ ਆਪਣੇ ਘੁਟਨਿਆਂ ਤੇ ਆਰਾਮ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਰੱਖੋ, ਸਰੀਰ ਅਤੇ ਮਨ ਨੂੰ ਸਹਿਜ ਭਾਵ ਵਿੱਚ ਰੱਖੋ । ਤਕਨੀਕ-ਪੇਟ ਨੂੰ ਫੈਲਾਉਂਦੇ ਹੋਏ ਹੌਲੀ-ਹੌਲੀ ਨੱਕ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਸਾਹ ਅੰਦਰ ਲਵੇ ਤੇ ਹੁਣ ਪੇਟ ਨੂੰ ਅੰਦਰ ਨੂੰ ਖਿਚਦੇ ਹੋਏ ਸਾਹ ਨੂੰ ਬਾਹਰ ਕੱਢੋ । ਇਸ ਤਰ੍ਹਾਂ ਕਰਨ ਨਾਲ ਫੇਫੜੇ ਆਪਣੇ ਕਪਾਲਭਾਤੀ ਪ੍ਰਾਣਾਯਾਮ ਆਪ ਹਵਾ ਨਾਲ ਭਰ ਜਾਣਗੇ । 10-15 ਵਾਰ ਤੇਜ਼ੀ ਨਾਲ ਸਾਹ ਲਉ ਤੇ ਛੱਡੋ ।

ਸਾਵਧਾਨੀਆਂ-

1. ਦਿਲ ਦੇ ਰੋਗੀ, ਉੱਚ ਰਕਤਚਾਪ, ਅਸਥਮਾ, ਹਰਣੀਆਂ ਦੇ ਰੋਗੀਆਂ ਨੂੰ ਇਹ ਵਿਆਯਾਮ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।
2. ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਖ਼ਾਲੀ ਪੇਟ ਹੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
3. ਦਰਦ ਜਾਂ ਚੱਕਰ ਆਉਣ ਲੱਗ ਜਾਣ ਤਾਂ ਇਹ ਵਿਆਯਾਮ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।

ਲਾਭ-

1. ਖੂਨ ਨੂੰ ਸਾਫ਼ ਕਰਦਾ ਹੈ ।
2. ਇਹ ਫੇਫੜੇ ਅਤੇ ਸਾਰੀ ਸਾਹ ਪ੍ਰਣਾਲੀ ਨੂੰ ਠੀਕ ਰੱਖਦਾ ਹੈ ।
3. ਇਸ ਨਾਲ ਸਰੀਰ ਨੂੰ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਵਿੱਚ ਆਕਸੀਜਨ ਮਿਲਦੀ ਹੈ ।
4. ਚਿੰਤਨ ਅਤੇ ਮੰਨਨ ਲਈ ਦਿਮਾਗ਼ ਨੂੰ ਤਿਆਰ ਕਰਦਾ ਹੈ ।
5. ਪਾਚਣ ਸ਼ਕਤੀ ਲਈ ਸੁਧਾਰ ਕਰਦਾ ਹੈ ।

PSEB 11th Class Physical Education Guide ਯੋਗ Important Questions and Answers

ਕੁੱਝ ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਪ੍ਰਸ਼ਨ
ਵਸਤੂਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ (Objective Type Questions)

ਪ੍ਰਸ਼ਨ 1.
‘ਠੀਕ ਢੰਗ ਨਾਲ ਕੰਮ ਕਰਨਾ ਹੀ ਯੋਗ ਹੈ । ਇਹ ਕਿਸ ਦਾ ਕਥਨ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਭਗਵਾਨ ਸ੍ਰੀ ਕ੍ਰਿਸ਼ਨ ਜੀ ਦਾ ਕਥਨ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਅਸ਼ਟਾਂਗ ਯੋਗ ਦੇ ਅੰਗ ਹਨ ?
(a) ਛੇ
(b) ਅੱਠ
(c) ਦਸ
(d) ਬਾਰਾਂ ।
ਉੱਤਰ-
(4) ਬਾਰਾਂ ।

ਪ੍ਰਸ਼ਨ 3.
ਆਸਣਾਂ ਦੀਆਂ ਕਿਸਮਾਂ ਹਨ ।
(a) ਦੋ
(b) ਚਾਰ
(c) ਛੇ
d) ਅੱਠ ।
ਉੱਤਰ-
(a) ਦੋ ।

ਪ੍ਰਸ਼ਨ 4.
ਸੂਰਜ ਭੇਦੀ ਪ੍ਰਾਣਾਯਾਮ, ਉਜਈ ਪ੍ਰਾਣਾਯਾਮ । ਇਹ ਕਿਸਦੇ ਭੇਦ ਹਨ ?
ਉੱਤਰ-
ਇਹ ਪ੍ਰਾਣਾਯਾਮ ਦੇ ਭੇਦ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਸਾਹ ਬਾਹਰ ਕੱਢਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਾਹ ਬਾਹਰ ਕੱਢਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਰੇਚਕ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਜਦੋਂ ਸਾਹ ਅੰਦਰ ਖਿੱਚਦੇ ਹਾਂ ਉਸ ਕਿਰਿਆ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਜਦੋਂ ਸਾਹ ਅੰਦਰ ਖਿੱਚਦੇ ਹਾਂ ਉਸ ਕਿਰਿਆ ਨੂੰ ਪੂਰਕ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਸਾਹ ਨੂੰ ਅੰਦਰ ਖਿੱਚਣ ਮਗਰੋਂ ਉੱਥੇ ਹੀ ਰੋਕਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਾਹ ਨੂੰ ਅੰਦਰ ਖਿੱਚਣ ਮਗਰੋਂ ਉੱਥੇ ਹੀ ਰੋਕਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਕੁੰਭਕ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਪ੍ਰਾਣਾਯਾਮ ਦੇ ਭੇਦ ਹਨ ।
(a) ਅੱਠ
(b) ਛੇ
(c) ਚਾਰ
(d) ਦੋ ।
ਉੱਤਰ-
(a) ਅੱਠ

ਪ੍ਰਸ਼ਨ 9.
ਸੂਰਜ ਨਮਸਕਾਰ ਦੀਆਂ ਕਿੰਨੀਆਂ ਸਥਿਤੀਆਂ ਹਨ ?
(a) ਬਾਰਾਂ
(b) ਅੱਠ
(c) ਛੇ
(d) ਚਾਰ ।
ਉੱਤਰ-
(a) ਬਾਰਾਂ ।

ਪ੍ਰਸ਼ਨ 10.
ਅਸ਼ਟਾਂਗ ਯੋਗ ਦੇ ਅੰਗ ਹਨ ।
(a) ਯਮ ।
(b) ਆਸਣ
(c) ਨਿਯਮ
(d) ਪ੍ਰਾਣਾਯਾਮ 1
ਉੱਤਰ-
ਉਪਰੋਕਤ ਸਾਰੇ ।

ਪ੍ਰਸ਼ਨ 11.
ਯੋਗ ਸ਼ਬਦ ਦਾ ਅਰਥ ਦੱਸੋ ।
ਉੱਤਰ-
ਯੋਗ ਦਾ ਅਰਥ ਜੁੜਨਾ ਜਾਂ ਮਿਲਣਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਆਸਣ ਕਿੰਨੇ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਆਸਣ ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 13.
ਸੂਰਜ ਨਮਸਕਾਰ ਵਿੱਚ ਕਿੰਨੀਆਂ ਅਵਸਥਾਵਾਂ ਹਨ ?
ਉੱਤਰ-
ਸੂਰਜ ਨਮਸਕਾਰ ਵਿਚ 12 ਅਵਸਥਾਵਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 14.
ਸੂਰਜ ਨਮਸਕਾਰ ਕਦੋਂ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਸੂਰਜ ਨਮਸਕਾਰ ਆਸਣ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਯੋਗ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਆਤਮਾ ਨੂੰ ਪਰਮਾਤਮਾ ਨਾਲ ਮਿਲਾਉਣ ਨੂੰ ਯੋਗ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 16.
ਆਤਮਾ ਨੂੰ ਪਰਮਾਤਮਾ ਨਾਲ ਮਿਲਾਨ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਆਤਮਾ ਨੂੰ ਪਰਮਾਤਮਾ ਨਾਲ ਮਿਲਾਨ ਨੂੰ ਯੋਗ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 17.
ਯੋਗ ਸੰਸਕ੍ਰਿਤ ਦੇ ਕਿਹੜੇ ਦੋ ਸ਼ਬਦਾਂ ਤੋਂ ਬਣਿਆ ਹੈ ?
ਉੱਤਰ-
‘ਯੁੱਜ’ ਤੋਂ ਬਣਿਆ ਹੈ, ਜਿਸ ਦਾ ਅਰਥ ਹੈ ਜੋੜ ਜਾਂ ਮੇਲ ।

ਪ੍ਰਸ਼ਨ 18.
ਸੂਰਜ ਨਮਸਕਾਰ ਕਦੋਂ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਸੂਰਜ ਨਮਸਕਾਰ ਆਸਨ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਯੋਗ ਦਾ ਕੋਈ ਇੱਕ ਮਹੱਤਵ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਮਨੁੱਖ ਦੀਆਂ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਬੁਨਿਆਦੀ ਸ਼ਕਤੀਆਂ ਦਾ ਵਿਕਾਸ ।
2. ਬੀਮਾਰੀਆਂ ਦੀ ਰੋਕਥਾਮ ਅਤੇ ਰੋਗਾਂ ਤੋਂ ਕੁਦਰਤੀ ਬਚਾਅ ।

ਪ੍ਰਸ਼ਨ 2.
ਸੂਰਜ ਨਮਸਕਾਰ ਦੇ ਕੋਈ ਦੋ ਲਾਭ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਸੂਰਜ ਨਮਸਕਾਰ ਤਾਕਤ, ਸ਼ਕਤੀ ਅਤੇ ਲਚਕ ਵਿਚ ਵਾਧਾ ਕਰਦਾ ਹੈ ।
2. ਇਹ ਇਕਾਗਰਤਾ ਵਧਾਉਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਆਸਣ ਕਿੰਨੇ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਆਸਣ ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ-

1. ਸਭਿਆਚਾਰਕ ਆਸਣ
2. ਆਰਾਮਦਾਇਕ ਆਸਣ ।

ਪ੍ਰਸ਼ਨ 4.
ਸ਼ਵ ਆਸਣ ਦੇ ਲਾਭ ਲਿਖੇ ।
ਉੱਤਰ-
1. ਇਸ ਆਸਣ ਨੂੰ ਕਰਨ ਨਾਲ ਸਰੀਰ ਤਰੋ-ਤਾਜ਼ਾ ਹੋ ਜਾਂਦਾ ਹੈ । ਸਵ-ਆਸਣ ਨਾਲ ਸਾਰੀਆ ਮਾਮਪੇਸ਼ੀਆ ਅਤੇ ਨਾਅ ਆਸਣ ਹਾਲਤ ਵਿਚ ਆ ਜਾਦੀਆ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਪਵਨ ਮੁਕਤ ਆਸਣ ਪਰਵਤ ਆਸਣ ਦੇ ਲਿਖੇ ।
ਉੱਤਰ-

1. ਪਾਚਨ ਪ੍ਰਣਾਲੀ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਦਾ ਹੈ ।
2. ਪੇਚਿਸ (Constipation) ਦੀ ਬਿਮਾਰੀ ਨੂੰ ਠੀਕ ਕਰਨ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ ।
3. ਗੈਸ ਦੀ ਬਿਮਾਰੀ ਨੂੰ ਦੂਰ ਕਰਦਾ ਹੈ ।
4. ਪਟ ਤੇ ਆਲੇ ਦੁਆਲੇ ਦੇ ਹਿੱਸੇ ਕੋਲੋਂ ਦੀ ਵਾਧੂ ਚਰਬੀ ਨੂੰ ਘਟਾਉਣ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਪ੍ਰਾਣਾਯਾਮ ਦੇ ਕੋਈ ਚਾਰ ਭੇਦ ਲਿਖੋ ।
ਉੱਤਰ-
ਪ੍ਰਾਣਾਯਾਮ ਦੇ ਕੋਈ ਚਾਰ ਭੇਦ ਇਸ ਤਰ੍ਹਾਂ ਹਨ-

1. ਤੂਰਜ ਭੱਦੀ ਪ੍ਰਾਣਾਯਾਮ
2. ਸ਼ੀਤਲੀ ਪ੍ਰਾਣਾਯਾਮ
3. ਸ਼ੀਤਕਾਰੀ ਪ੍ਰਾਣਾਯਾਮ
4. ਉਜਈ ਪ੍ਰਾਣਾਯਾਮ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਯੋਗ ਆਸਣ ਕਰਨ ਸਮ ਕੋਈ ਚਾਰ ਦਿਸ਼ਾ ਨਿਰਦੇਸ਼ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਯੋਗ ਆਸਣ ਕਰਨ ਵੇਲੇ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਸੂਰਜ ਨੂੰ ਨਮਸਕਾਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
2. ਜਗ ਮਣ ਕਿਸੇ ਮਾਹਿਰ ਦੇਖ ਰੇਖ ਵਿਚ ਹੀ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ । ਨੂੰ ਸਭ ਤੋ ਪਹਿਲਾ
3. ਮਦਾਇਕ ਅਤੇ ਫਿਰ ਸਭਿਆਚਾਰਕ ਆਸਣ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ ।
4. ਯੋਗ ਕਰਨ ਸਮੇਂ ਮਾਹ ਅੰਦਰ ਲੈ ਕੇ ਜਾਣ ਅਤੇ ਬਾਹਰ ਕੱਢਣ ਦੀ ਕਿਰਿਆ ਦੀ ਤਰਤੀਬ ਠੀਕ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਤਾਂ ਹੀ ਯੋਗ ਦਾ ਫਾਇਦਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸੂਰਜ ਨਮਸਕਾਰ ਵਿਚ ਪਹਿਲੀਆਂ ਚਾਰ ਮੁਦਰਾ ਬਾਰੇ ਲਿਖੋ । ਉੱਤਰ-

1. ਦੋਨੋਂ ਹੱਥ ਅਤੇ ਪੈਰ ਜੋੜ ਕੇ ਨਮਸਕਾਰ ਦੀ ਮੁਦਰਾ ਵਿਚ ਸਿੱਧੇ ਖੜੇ ਹੋ ਜਾਓ ।
2. ਸਾਹ ਅੰਦਰ ਖਿੱਚਦੇ ਹੋਏ ਦੋਨੋਂ ਬਾਹਾਂ ਨੂੰ ਸਿਰ ਦੇ ਉੱਪਰ ਲੈ ਜਾਓ ਅਤੇ ਕਮਰ ਨੂੰ ਮੋੜਦੇ ਹੋਏ ਥੋੜ੍ਹਾ ਪਿੱਛੇ ਨੂੰ ਝੁਕ ਜਾਓ ।
3. ਸਾਹ ਬਰਾਬਰ ਛਡਦੇ ਹੋਏ ਦੋਨੋਂ ਹੱਥਾਂ ਨਾਲ ਜ਼ਮੀਨ ਨੂੰ ਛੂਹਣਾ ਹੈ ਅਤੇ ਮੱਥਾ ਗੋਡਿਆਂ ਨੂੰ ਲਗਾਉਣਾ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਗੋਡੇ ਸਿੱਧੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
4. ਸੰਜੀ ਲੱਤ ਪਿੱਛੇ ਨੂੰ ਸਿੱਧੀ ਕਰ ਦਿਓ । ਖੱਬਾ ਪੈਰ ਦੋਨੋਂ ਹਥੇਲੀਆਂ ਵਿਚ ਰਹੇਗਾ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਕੁਝ ਸੈਕਿੰਡ ਲਈ ਰੁਕੋ ।

ਪ੍ਰਸ਼ਨ 3.
ਯੋਗ ਕਰਨ ਦੇ ਕੋਈ ਦੋ ਮਹੱਤਵ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਯੋਗ ਨਾਲ ਮਨੁੱਖ ਦੀਆਂ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਬੁਨਿਆਦੀ ਸ਼ਕਤੀਆਂ ਵਿਕਸਿਤ ਹੁੰਦੀਆਂ ਹਨ । ਪਾਣਾਯਾਮ ਦੁਆਰਾ ਫੇਫੜਿਆਂ ਵਿਚ ਬਹੁਤ ਸਾਰੀ ਹਵਾ ਚਲੀ ਜਾਂਦੀ ਹੈ । ਜਿਸ ਨਾਲ ਫੇਫੜਿਆਂ ਦੀ ਕਸਰਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਫੇਫੜਿਆਂ ਦੇ ਬਹੁਤ ਸਾਰੇ ਰੋਗ ਦੂਰ ਹੁੰਦੇ ਹਨ ।
2. ਯੋਗਾ ਅਭਿਆਸ ਕਰਨ ਨਾਲ ਸਰੀਰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਸਵਸਥ ਰਹਿੰਦਾ ਹੈ । ਧੋਤੀ ਕਿਰਿਆ ਅਤੇ ਬਸਤੀ ਕਿਰਿਆ ਕੁਮਵਾਰ ਜਿਗਰ ਤੇ ਅੰਤੜੀਆਂ ਨੂੰ ਤੂ ਰੱਖਦੀ ਹੈ ਹਾਫ ਸਰੀਰ ਸਦਾ ਹੀ ਨਿਰੋਗ ਰਹਿੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਅਸ਼ਟਾਂਗ ਯੋਗ ਦੇ ਅੰਗਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਯਮ
2. ਨਿਯਮ
3. ਆਸਣ
4. (ਪ੍ਰਾਣਾਯਾਮ
5. ਤਿਅਹਾਰ
6. ਧਾਰਨਾ
7. ਧਿਆਨ (Meditation)
8. ਸਮਾਧੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਪਦਮ ਆਸਣ ਦੀ ਵਿਧੀ ਲਿਖੋ ।
ਉੱਤਰ-
ਵਿਧੀ-

• ਜ਼ਮੀਨ ‘ਤੇ ਬੈਠ ਜਾਓ ਅਤ ਹਲੀ-ਹਲੀ ਸੱਜੀ ਲੱਤ ਨੂੰ ਮੋੜਦੇ ਹੋਏ ਸੱਜਾ ਪੈਰ ਖੱਬੇ ਪੱਟ ‘ਤੇ ਰੱਖੋ ।
• ਫਿਰ ਖੱਬੀ ਲੱਤ ਨੂੰ ਮੰੜਦੇ ਹੋਏ ਖਬਾ ਪੈਰ ਸੱਜੇ ਪੱਟ ‘ਤੇ ਰੱਖੋ ਤੇ ਫਿਰ ਜਣਨ ਮੁਦਰਾ ਵਿਚ ਬੈਠੋ । ਜਣਨ ਮੁਦਰਾ | ਲਈ ਹੱਥ ਦੀ ਪਹਿਲੀ ਉਗਲੀ ( Index fit; ਅਤੇ ਅੰਗੂਠੇ ਦੇ ਕੋਨੇ ਮਿਲਾਓ | ਬਾਕੀ ਦੀਆਂ ਉਂਗਲੀਆਂ ਸਿੱਧੀਆਂ ਰੱਖੋ ।
• ਫਿਰ ਇਸ ਮੁਦਰਾ ਵਿਚ ਹੱਥ ਗਡਿਆਂ ‘ਤੇ ਰੱਖੋ । ਪਿੱਠ ਸਿੱਧੀ ਰੱਖੋ ਅਤੇ ਪਦਮ ਆਸਣ ਦੀ ਸਥਿਤੀ ਤੋਂ ਵਾਪਸ ਆਉਂਦੇ ਸਮੇਂ ਪਹਿਲਾਂ ਖੱਬੀ ਲਤ ਸਜੇ ਪੱਟ ਤੋਂ ਉਤਾਰ ਅਤੇ ਸੱਜੀ ਲੱਤ ਹਟਾਓ ਅਤੇ ਪਹਿਲੀ ਸਥਿਤੀ ਵਿਚ ਵਾਪਸ ਆ ਜਾਓ ।

ਪ੍ਰਸ਼ਨ 6.
ਸ਼ਵ-ਆਸਣ ਦੇ ਲਾਭ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਇਸ ਆਸਣ ਨੂੰ ਕਰਨ ਨਾਲ ਥਕਾਵਟ ਦੂਰ ਹੁੰਦੀ ਹੈ ਅਤੇ ਦਿਮਾਗ ਚਿੰਤਾ ਮੁਕਤ ਹੋ ਜਾਂਦਾ ਹੈ ।
2. ਸ਼ਵ-ਆਸਣ ਕਰਨ ਨਾਲ ਸਾਰੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਅਤੇ ਨਾੜੀਆਂ ਆਰਾਮ ਦੀ ਹਾਲਤ ਵਿਚ ਆ ਜਾਂਦੀਆਂ ਹਨ ।
3. ਇਸ ਆਸਣ ਨੂੰ ਕਰਨ ਨਾਲ ਸਰੀਰ ਤਰੋ-ਤਾਜ਼ਾ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਵੱਡੇ ਉੱਤਰ ਵਾਲਾ ਪ੍ਰਸ਼ਨ (Long Answer Type Question)

ਪ੍ਰਸ਼ਨ 1.
ਯੋਗ ਦਾ ਅਰਥ ਅਤੇ ਮਨੁੱਖੀ ਜੀਵਨ ਵਿਚ ਇਸਦੇ ਮਹੱਤਵ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿਓ ।
ਉੱਤਰ-
ਯੋਗ ਦਾ ਅਰਥ – ਯੋਗ ਸ਼ਬਦ ਸੰਸਕ੍ਰਿਤ ਦੇ ‘ਯੁੱਚ’ ਸ਼ਬਦ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ । ਜਿਸ ਦਾ ਅਰਥ ਜੋੜਨਾ ਜਾਂ ਮੇਲ ਹੈ । ਇਸ ਦਾ ਭਾਵ ਹੈ ਕਿ ਯੋਗ ਉਹ ਕਿਰਿਆ ਜਾਂ ਸਾਧਨ ਹੈ ਜਿਸ ਨਾਲ ਆਤਮਾ ਪਰਮਾਤਮਾ ਨਾਲ ਮਿਲਦੀ ਹੈ । ਯੋਗ ਰਾਹੀਂ ਅਸੀਂ ਮਨ ਅਤੇ ਸਰੀਰ ਦੋਨਾਂ ਨੂੰ ਚਿੰਤਾ ਅਤੇ ਬਿਮਾਰੀਆਂ ਤੋਂ ਮੁਕਤ ਕਰਕੇ ਤੰਦਰੁਸਤ ਸਰੀਰ ਪ੍ਰਾਪਤ ਕਰ ਲੈਂਦੇ ਹਾਂ । ਇਹ ਭਾਰਤ ਦੀ ਹਜ਼ਾਰਾਂ ਸਾਲ ਪੁਰਾਣੀ ਵਿਧੀ ਹੈ ।

ਮਨੁੱਖੀ ਜੀਵਨ ਵਿਚ ਇਸਦਾ ਮਹੱਤਵ – ਯੋਗ ਦੀ ਮਨੁੱਖੀ ਜੀਵਨ ਲਈ ਬਹੁਤ ਮਹੱਤਤਾ ਹੈ | ਯੋਗ ਭਾਰਤ ਦਾ ਹੀ ਨਹੀਂ, ਸਗੋਂ ਦੁਨੀਆਂ ਦਾ ਪਾਚੀਨ ਗਿਆਨ ਹੈ । ਦੇਸ਼ਾਂ-ਵਿਦੇਸ਼ਾਂ ਵਿਚ ਡਾਕਟਰਾਂ ਅਤੇ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਅਧਿਆਪਕਾਂ ਨੇ ਇਸ ਗਿਆਨ ਦਾ ਸਿੱਕਾ ਮੰਨਿਆ ਹੈ । ਯੋਗ ਨਾਲ ਸਰੀਰ ਅਤੇ ਮਨ ਤੰਦਰੁਸਤ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਇਸਦੇ ਨਾਲ-ਨਾਲ ਨਾੜੀਆਂ ਵੀ ਲਚਕਦਾਰ ਅਤੇ ਮਜ਼ਬੂਤ ਰਹਿੰਦੀਆਂ ਹਨ | ਯੋਗ ਸਰੀਰ ਨੂੰ ਬਿਮਾਰੀ ਤੋਂ ਦੂਰ ਰੱਖਦਾ ਹੈ ਅਤੇ ਜੇ ਕੋਈ ਬਿਮਾਰੀ ਲੱਗ ਜਾਵੇ ਤਾਂ ਉਸ ਨੂੰ ਆਸਣ ਜਾਂ ਯੋਗ ਦੀਆਂ ਦੂਸਰੀਆਂ ਕਿਰਿਆਵਾਂ ਨਾਲ ਠੀਕ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਜਿੱਥੇ ਯੋਗ ਮਨੁੱਖ ਨੂੰ ਤੰਦਰੁਸਤ, ਸੁੰਦਰ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣਾਉਂਦਾ ਹੈ, ਉੱਥੇ ਇਹ ਸ਼ਖ਼ਸੀਅਤ ਨੂੰ ਚਾਰ ਚੰਨ ਲਾ ਦਿੰਦਾ ਹੈ । ਸੱਚ ਤਾਂ ਇਹ ਹੈ ਕਿ ਯੋਗ ਸਾਨੂੰ ਉਸ ਦੁਨੀਆਂ ਵਿਚ ਲੈ ਜਾਂਦਾ ਹੈ ਜਿੱਥੇ ਜੀਵਨ ਹੈ, ਤੰਦਰੁਸਤੀ ਹੈ, ਪਰਮ ਸੁੱਖ ਹੈ, ਮਨ ਦੀ ਸ਼ਾਂਤੀ ਹੈ । ਯੋਗ ਤਾਂ ਗਿਆਨ ਦੀ ਉਹ ਗੰਗਾ ਹੈ ਜਿਸ ਦੀ ਹਰੇਕ ਬੂੰਦ ਵਿਚ ਰੋਗ ਨਸ਼ਟ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਹੈ । ਯੋਗ ਪਰਮਾਤਮਾ ਦੇ ਨਾਲ ਮਿਲਣ ਦਾ ਸਰਵਉੱਤਮ ਸਾਧਨ ਹੈ ।

ਸਰੀਰ ਆਤਮਾ ਅਤੇ ਪਰਮਾਤਮਾ ਦੇ ਮਿਲਣ ਦਾ ਮਾਧਿਅਮ ਹੈ ਤੇ ਇਕ ਤੰਦਰੁਸਤ ਸਰੀਰ ਦੁਆਰਾ ਹੀ ਪਰਮਾਤਮਾ ਦੇ ਦਰਸ਼ਨ ਕੀਤੇ ਹਨ | ਯੋਹਾ ਮਨੁੱਖ ਨੂੰ ਤੰਦਰੁਸਤ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣਾਉਣ ਦੇ ਨਾਲ ਉਸ ਨੂੰ ਸੁਯੋਗ ਅਤੇ ਗੁਣੀ ਵੀ ਬਣਾ : ਇਹ ਸਾਡੇ ਵਿਚ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਯੋਗ ਕੇਵਲ ਰੋਗੀ ਵਿਅਕਤੀਆਂ ਲਈ ਹੀ ਲਾਭਕਾਰੀ ਨਹੀਂ, ਸਗੋਂ ਸਵਸਥ ਮਨੁੱਖ ਵੀ ਇਸ ਦੇ ਅਭਿਆਸ ਤੋਂ ਲਾਭ ਉਠਾ ਸਕਦੇ ਹਨ | ਯੋਗ ਹਰ ਇੱਕ ਉਮਰ ਦੇ ਵਿਅਕਤੀਆ ਲਈ ਗੁਣਕਾਰੀ ਹੈ । ਇਸਦੇ ਅਭਿਆਸ ਨਾਲ ਸਰੀਰ ਦੇ ਸਾਰੇ ਅੰਗ ਠੀਕ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਨ ਲੱਗ ਪੈਂਦੇ ਹਨ | ਯੋਗ ਅਭਿਆਸ ਨਾਲ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਦਿਮਾਗੀ ਸੰਤੁਲਨ ਵਧਦਾ ਹੈ । ਯੋਗ ਦੀ ਜ਼ਰੂਰਤ ਅੱਜ ਦੇ ਯੁੱਗ ਵਿਚ ਵੀ ਉਨੀ ਹੀ ਹੈ ਜਿੰਨੀ ਪਹਿਲਾਂ ਦੇ ਯੁੱਗ ਵਿਚ ਸੀ । ਸਾਡੇ ਦੇਸ਼ ਨਾਲੋਂ ਬਾਹਰਲੇ ਦੇਸ਼ਾਂ ਵਿਚ ਇਸ ਖੇਤਰ ਵਿਚ ਬਹੁਤ ਉੱਨਤੀ ਹੋਈ ਹੈ । ਉਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਵਿਚ ਮਨ ਦੀ ਸ਼ਾਂਤ ਵਾਸਤੇ ਇਸ ਦਾ ਬਹੁਤ ਪ੍ਰਚਾਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਵਿਚ ਯੋਗ ਦੇ ਖੇਤਰ ਵਿਚ ਬਹੁਤ ਵਿਦਵਾਨ ਹਨ | ਅੱਜ ਦੇ ਯੁੱਗ ਵਿਚ ਵੀ ਮਨੁੱਖ ਯੋਗ ਤੋਂ ਪੂਰਾ ਲਾਭ ਉਠਾ ਸਕਦਾ ਹੈ ।

Punjab State Board PSEB 10th Class Physical Education Book Solutions ਐਥਲੈਟਿਕਸ (Athletics) Game Rules.

ਐਥਲੈਟਿਕਸ (Athletics) Game Rules – PSEB 10th Class Physical Education

ਐਥਲੈਟਿਕਸ ਦਾ ਇਤਿਹਾਸ
(History of Athletics)

ਐਥਲੈਟਿਕਸ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਨਸ਼ੀਲੀਆਂ ਦਵਾਈਆਂ ਖਾ ਕੇ ਮੁਕਾਬਲੇ ਵਿਚ ਹਿੱਸਾ ਨਹੀਂ ਲੈ ਸਕਦੇ | ਜਿਹੜਾ ਐਥਲੀਟ ਕਿਸੇ ਹੋਰ ਐਟ ਲਈ ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੀ ਰੁਕਾਵਟ ਪੈਦਾ ਕਰਦਾ ਹੈ, ਉਸ ਨੂੰ ਮੁਕਾਬਲੇ ਵਿਚੋਂ ਬਾਹ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਜਿਹੜਾ ਐਥਲੀਟ ਦੌੜਦੇ ਹੋਏ ਟਰੈਕ ਆਪਣੀ ਮਰਜੀ ਨਾਨ ਨੂੰ , ਦਿੰਦਾ ਹੈ, ਉਹ ਦੁਬਾਰਾ ਦੌੜ ਜਾਰੀ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਫੀਲਡ ਈਵੈਂਟਸ ਵਿਚ ਤ ਦੇ ਈਵੈਂਟਸ ਆਉਂਦੇ ਹਨ, ਜੰਪਿੰਗ ਅਤੇ ਥਰੋ ਇਵੈਂਟਸ, ਟਰੈਕ ਇਵੈਟਸ ਵਿਚ ਉਹ ਦੌੜਾਂ ਆਉਂਦੀਆਂ ਹਨ ਜੋ ਟਰੈਕ ਵਿਚ ਦੌੜੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।

200 ਮੀਟਰ ਦੇ ਟਰੈਕ ਦੀ ਲੰਬਾਈ 40 ਮੀਟਰ ਤੇ ਚੌੜਾਈ 38.18 ਮੀਟਰ, 400 ਮੀਟਰ ਦੇ ਟਰੰਕ ਦੀ ਲੰਬਾਈ 7 ਮੀਟਰ ਤੇ ਚੌੜਾਈ 67 ਮੀਟਰ ਹੁੰਦੀ ਹੈ :
ਜੈਵਲੀ ਦਾ ਭਾਤੁ ਲੜਕਿਆਂ ਲਈ 805-825 ਗ੍ਰਾਮ ਅਤੇ ਕੁੜੀਆਂ ਲਈ 605-620 4 ਤਕ ਹੁੰਦਾ ਹੈ । ਡਿਸਕਸ ਦਾ ਭਾਰ ਮੁੰਡਿਆਂ ਲਈ 2 ਕਿਲੋਗ੍ਰਾਮ ਹੈ ।
ਗੋਲਾਮ ਡਿਸਕਸ ਸੁੱਟਣ ਤੋਂ ਜ਼ਰੂਰੀ ਹੈ ਕਿ 400 ਦੇ ਸੈਂਟਰ ਵਿਚ ਹੀ ਸੁੱਟਣ ਵਾਲਾ ਖ਼ ਣ ਤੋਂ ਬਅਦ ਪੈਰ ਰੱਖੇ । ਗਲੇ ਦਾ ਭਾਰ 7.2 ਕਿਲੋ ਹੈ : ਮੁੰਡਿਆਂ ਲਈ 110 ਮੀਟਰ ਹਰਡਲਜ਼ ਦੀ ਉੱਚਾਈ 1.06 ਮੀਟਰ ਅਤੇ ਜੂਨੀ ਲੜਕੀਆਂ ਲਈ 100 ਮੀਟਰ ਹਰਡਲਜ ਦੀ ਉੱਚਾਈ 0.75 ਮੀਟਰ ਹੁੰਦੀ ਹੈ ਸੀਨੀਅਰ ਲੜਕੀਆਂ ਲਈ ਇਹ ਉੱਚਾਈ 0.84 ਮੀਟਰ ਹੋਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 1.
ਐਥਲੈਟਿਕਸ ਮੁਕਾਬਲਾ ਕਰਵਾਉਣ ਲਈ ਕਿਹੜੇ-ਕਿਹੜੇ ਅਧਿਕਾਰੀਆਂ ਦੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਐਥਲੈਟਿਕਸ ਮੁਕਾਬਲੇ ਕਰਵਾਉਣ ਲਈ ਹੇਠ ਲਿਖੇ ਅਧਿਕਾਰੀਆਂ ਦੀ – ਹੁੰਦੀ ਹੈ –
ਪ੍ਰਬੰਧਕ ਅਧਿਕਾਰੀ (Administrative Officials)-

1. ਮੈਨੇਜਰ (Manager)
2. ਸਕੱਤਰ (Secretary)
3. ਤਕਨੀਕੀ ਮੈਨੇਜਰ (Technical Manager) ।

ਮੁਕਾਬਲੇ ਲਈ ਅਧਿਕਾਰੀ (Officials for the meet) –

• ਰੈਫਰੀ ਟਰੈਕ ਵਾਸਤੇ (Referee for Track events)
• ਰੈਫਰੀ ਫੀਲਡ ਈਵੈਂਟਸ ਵਾਸਤੇ (Referee for Field events)
• ਰੈਫਰੀ ਵਾਕਿੰਗ ਈਵੈਂਟਸ ਵਾਸਤੇ (Referee for Walking events)
• ਜੱਜ ਟਰੈਕ ਈਵੈਂਟਸ ਵਾਸਤੇ (Judge for Track events)
• ਜੱਜ ਫੀਲਡ ਈਵੈਂਟਸ ਵਾਸਤੇ ( Judge for Field events)
• ਜੱਜ ਵਾਕਿੰਗ ਈਵੈਂਟਸ ਵਾਸਤੇ (Judge for Walking events)
• ਅੰਪਾਇਰ (Umpire)
• ਟਾਈਮ ਕੀਪਰ (Time Keeper)
• ਸਟਾਰਟਰ (Starter)
• ਸਹਾਇਕ ਸਟਾਰਟਰ (Asstt. Starter)
• ਮਾਰਕ ਮੈਨ (Mark man)
• ਲੈਪ ਸਕੋਰਰ (Lap Scorer)
• ਰੀਕਾਰਡਰ (Recorder)
• ਮਾਰਸ਼ਲ (Marshal) ।

ਹੇਰ ਵਾਧ ਅਧਿਕਾਰੀ (Additional Officials)-

1. ਅਨਾਊਂਸਰ (Announcer)
2. ਆਫੀਸ਼ਲ ਸਰਵੇਅਰ (Official Surveyer)
3. ਡਾਕਟਰ (Doctor)
4. ਸਟੂਅਰਡਜ਼ (Stewards)

ਟਰੈਕ ਈਵੈਂਟਸ ਮਰਦਾਂ ਲਈ
100 ਮੀਟਰ ਰੇਸ
200 ਮੀਟਰ ਰੇਮ
400 ਮੀਟਰ ਰੇਸ
800 ਮੀਟਰ ਰੇਸ
1500 ਮੀਟਰ ਰੇਸ
3,000 ਮੀਟਰ ਰੇਸ
5,000 ਮੀਟਰ ਰੇਸ
10,000 ਮੀਟਰ ਰੇਸ
42195 ਮੀਟਰ ਜਾਂ 26 ਮੀਲ ਰੇਸ
3000 ਮੀਟਰ ਸਟੀਪਲ ਚੇਜ
20,000 ਮੀਟਰ ਵਾਕਿੰਗ
30,000 ਮੀਟਰ ਵਾਕਿੰਗ
50,000 ਮੀਟਰ ਵਾਕਿੰਗ

ਇਸਤਰੀਆਂ ਲਈ ਟਰੈਕ ਈਵੈਂਟਸ
100 ਮੀਟਰ ਰੇਸ
200 ਮੀਟਰ ਰੇਸ
400 ਮੀਟਰ ਰੇਸ
800 ਮੀਟਰ ਰੇਸ
1500 ਮੀਟਰ ਰੇਸ

ਹਰਡਲ ਦੌੜਾਂ ਮਰਦਾਂ ਵਾਸਤੇ

110 ਮੀਟਰ ਹਰਡਲ ਰੇਸ
200 ਮੀਟਰ ਹਰਡਲ ਰੇਸ
400 ਮੀਟਰ ਹਰਡਲ ਰੇਸ਼

ਇਸਤਰੀਆਂ ਲਈ ਹਰਡਲ ਦੌੜ

100 ਮੀਟਰ ਹਰਡਲ ਦੌੜ
200 ਮੀਟਰ ਹਰਡਲ ਦੌੜ

ਰੀਲੇ ਦੌੜਾਂ ਮਰਦਾਂ ਲਈ

4 x 100 ਮੀਟਰ
4 x 200 ਮੀਟਰ
4 x 400 ਮੀਟਰ
4 x 800 ਮੀਟਰ
4 x 1500 ਮੀਟਰ

ਰੀਲੇ ਦੌੜਾਂ ਇਸਤਰੀਆਂ ਲਈ
4 x 100 ਮੀਟਰ
4 x 200 ਮੀਟਰ
4 x 400 ਮੀਟਰ
ਮੈਡਲੇ ਰਿਲੇ ਰੇਸ
800 x 200 x 200 x 400

ਪ੍ਰਸ਼ਨ 2.
ਟਰੈਕ ਈਵੈਂਟਸ ਲਈ ਐਥਲੀਟਾਂ ਲਈ ਨਿਰਧਾਰਿਤ ਨਿਯਮਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਟਰੈਕ ਈਵੈਂਟਸ ਦੇ ਨਿਯਮ ਐਥਲੀਟਾਂ ਵਾਸਤੇ ਇਸ ਤਰ੍ਹਾਂ ਹਨ –

• ਖਿਡਾਰੀ ਅਜਿਹੇ ਕੱਪੜੇ ਪਾਉਣ, ਜੋ ਕਿਸੇ ਕਿਸਮ ਦੇ ਇਤਰਾਜ਼ ਯੋਗ ਨਾ ਹੋਣ ! ਉਹ ਸਾਫ਼ ਵੀ ਹੋਣ ।
• ਐਥਲੀਟ ਨੰਗੇ ਪੈਰ ਜਾਂ ਜੁੱਤੀਆਂ ਪਾ ਕੇ ਇਕ ਪੈਰ ਜਾਂ ਦੋਹਾਂ ਪੈਰਾਂ ਵਿਚ ਖੇਡ ਵਿਚ ਹਿੱਸਾ ਲੈ ਸਕਦੇ ਹਨ । ਜੁੱਤੀਆਂ ਇਸ ਕਿਸਮ ਦੀਆਂ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ, ਜੋ ਖਿਡਾਰੀਆਂ ਨੂੰ ਖੇਡ ਵਿਚ ਹੋਰ ਮੱਦਦ ਨਾ ਦੇਣ ।
• ਜੋ ਖਿਡਾਰੀ ਹੋਰ ਖਿਡਾਰੀਆਂ ਲਈ ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੀ ਰੁਕਾਵਟ ਪੈਦਾ ਕਰਦਾ ਹੈ ਜਾਂ ਪ੍ਰਗਤੀ ਦੇ ਰਾਹ ਵਿਚ ਰੁਕਾਵਟ ਬਣਦਾ ਹੈ, ਉਸ ਨੂੰ ਅਯੋਗ ਠਹਿਰਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
• ਹਰੇਕ ਖਿਡਾਰੀ ਨੂੰ ਆਪਣੇ ਅੱਗੇ ਅਤੇ ਪਿੱਛੇ ਸਪੱਸ਼ਟ ਰੂਪ ਵਿਚ ਨੰਬਰ ਲਾਉਣੇ ਚਾਹੀਦੇ ਹਨ !
• ਲਾਈਨਾਂ (Lines) ਵਿਚ ਦੌੜੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਦੌੜਾਂ ਵਿਚ ਖਿਡਾਰੀ ਨੂੰ ਸ਼ੁਰੂ ਤੋਂ ਅਖੀਰ ਤਕ ਆਪਣੀ ਲਾਈਨ ਵਿਚ ਹੀ ਰਹਿਣਾ ਹੋਵੇਗਾ ।
• ਜੇਕਰ ਕੋਈ ਖਿਡਾਰੀ ਜਾਣ-ਬੁੱਝ ਕੇ ਆਪਣੀ ਲੇਨ ਵਿਚੋਂ ਬਾਹਰ ਦੌੜਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਅਯੋਗ ਠਹਿਰਾਇਆ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਰੈਫਰੀ ਦੀ ਸਮਝ ਅਨੁਸਾਰ ਅਜਿਹਾ ਉਸ ਨੇ ਜਾਣ-ਬੁੱਝ ਕੇ ਨਹੀਂ ਕੀਤਾ ਤਾਂ ਉਸਦੀ ਮਰਜ਼ੀ ਹੈ ਕਿ ਉਹ ਉਸ ਨੂੰ ਅਯੋਗ ਠਹਿਰਾਏ ਜਾਂ ਨਾ ।
• ਜੇ ਖਿਡਾਰੀ ਆਪਣੀ ਮਰਜ਼ੀ ਨਾਲ ਟਰੈਕ ਨੂੰ ਛੱਡਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਦੁਬਾਰਾ ਦੌੜ ਜਾਰੀ ਰੱਖਣ ਦਾ ਅਧਿਕਾਰ ਨਹੀਂ ।
• ਜੇਕਰ ਟਰੈਕ ਅਤੇ ਫੀਲਡ ਦੋਵੇਂ ਈਵੈਂਟਸ ਇੱਕੋ ਵਾਰੀ ਸ਼ੁਰੂ ਹੋ ਚੁੱਕੇ ਹੋਣ, ਤਾਂ ਜੱਜ ਉਸ ਨੂੰ ਵੱਖ-ਵੱਖ ਢੰਗਾਂ ਨਾਲ ਹਿੱਸਾ ਲੈਣ ਦੀ ਆਗਿਆ ਦੇ ਸਕਦਾ ਹੈ ।
• ਫੀਲਡ ਈਵੈਂਟਸ ਵਿਚ ਕਿਸੇ ਖਿਡਾਰੀ ਦੇ ਗੈਰ ਜ਼ਰੂਰੀ ਦੇਰੀ ਕਰਨ ਉੱਤੇ ਉਸ ਦੇ ਵਿਰੁੱਧ ਇਕ ਦੋਸ਼ ਦਰਜ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਉਸ ਨੂੰ ਟਰਾਇਲ ਵਿਚ ਹਿੱਸਾ ਨਹੀਂ ਲੈਣ ਦਿੱਤਾ ਜਾਂਦਾ । ਜੇਕਰ ਫਿਰ ਵੀ ਉਹ ਅਜਿਹਾ ਕਰਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਹੋਰ ਟਰਾਇਲ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਦੀ ਆਗਿਆ ਨਹੀਂ ਦਿੱਤੀ ਜਾਵੇਗੀ, ਪਰ ਉਸਦਾ ਪਹਿਲਾ ਪ੍ਰਦਰਸ਼ਨ ਮੰਨ ਲਿਆ ਜਾਵੇਗਾ ।
• ਖਿਡਾਰੀ ਨੂੰ ਨਸ਼ੀਲੀਆਂ ਵਸਤੂਆਂ ਅਤੇ ਦਵਾਈਆਂ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦੀ ਆਗਿਆ ਨਹੀਂ ਅਤੇ ਨਾ ਹੀ ਖੇਡਦੇ ਸਮੇਂ ਇਹਨਾਂ ਨੂੰ ਆਪਣੇ ਕੋਲ ਰੱਖ ਸਕਦਾ ਹੈ। ਜੇਕਰ ਕੋਈ ਖਿਡਾਰੀ ਅਜਿਹੀ ਦਵਾਈ ਦੀ ਵਰਤੋਂ ਕਰਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਅਯੋਗ ਠਹਿਰਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
• 800 ਮੀਟਰ ਦੌੜ (800 Metre Race) ਦਾ ਸਟਾਰਟਰ ਆਪਣੀ ਹੀ ਭਾਸ਼ਾ ਵਿਚ ਕਹੇਗਾ, “On your marks” ….. ਪਿਸਤੌਲ ਚਲਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਖਿਡਾਰੀ ਦੌੜ ਪੈਂਦੇ ਹਨ । 800 ਮੀਟਰ ਤੋਂ ਵੱਧ ਦੀਆਂ ਦੌੜਾਂ ਵਿਚ ਸਿਰਫ ‘On your marks’’ ਸ਼ਬਦ ਕਹੇ ਜਾਣਗੇ ਅਤੇ ਫਿਰ ਤਿਆਰ ਹੋਣ ਤੇ ਪਿਸਤੌਲ ਚਲਾ ਦਿੱਤਾ ਜਾਵੇਗਾ ।
• ਖਿਡਾਰੀ ਨੂੰ “On your marks’ ਦੀ ਹਾਲਤ ਵਿਚ ਆਪਣੇ ਸਾਹਮਣੇ ਵਾਲੀ ਗਰਾਊਂਡ ਤੇ ਆਰੰਭ ਰੇਖਾ (Start lilie) ਨੂੰ ਹੱਥਾਂ ਜਾਂ ਪੈਰਾਂ ਰਾਹੀਂ ਛੂਹਣਾ ਨਹੀਂ ਚਾਹੀਦਾ ।
• ਜੇਕਰ ਕੋਈ ਖਿਡਾਰੀ ਪਿਸਤੌਲ ਦੇ ਸ਼ਾਟ ਤੋਂ ਪਹਿਲਾਂ ਆਰੰਭ ਰੋਖਾ ਨੂੰ ਪਾਰ ਕਰਦਾ ਹੈ, ਉਸ ਨੂੰ ਆਰੰਭ (ਸਟਾਰਟ) ਫਾਉਲ ਹੋਵੇਗਾ । ਇਸ ਤੇ ਉਸ ਨੂੰ ਚਿਤਾਵਨੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਜਦ ਉਹ ਦੋ ਵਾਰੀ ਅਜਿਹਾ ਕਰਦਾ ਹੈ ਪੈਂਟਾਥਲੋਨ ਜਾਂ ਡੈਕੇਲੋਨ ਵਿਚ ਤਿੰਨ ਵਾਰੀ ਤਾਂ ਉਸ ਨੂੰ ਅਯੋਗ ਘੋਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।
• ਖਿਡਾਰੀਆਂ ਦੀ ਪੁਜੀਸ਼ਨ ਦਾ ਫ਼ੈਸਲਾ ਅੰਤਿਮ ਰੇਖਾ ਤੇ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਖਿਡਾਰੀ ਦੇ ਸਰੀਰ ਦਾ ਕੋਈ ਵੀ ਹਿੱਸਾ ਅੰਤਿਮ ਰੇਖਾ ਨੂੰ ਪਹਿਲਾਂ ਛੂਹ ਜਾਵੇ, ਉਸ ਨੂੰ ਪਹਿਲਾਂ ਪਹੁੰਚਿਆ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।
• ਹਰਡਲ ਦੌੜ ਵਿਚ ਜੋ ਖਿਡਾਰੀ ਹੱਥਾਂ ਜਾਂ ਟੰਗਾਂ ਨੂੰ ਫੈਲਾ ਕੇ ਹੋਰ ਖਿਡਾਰੀਆਂ ਲਈ ਰੁਕਾਵਟ ਬਣਦਾ ਹੈ ਅਤੇ ਉਹਨਾਂ ਦੀ ਲੇਨ ਵਿਚ ਸਥਿਰ ਹਰਡਲ ਨੂੰ ਪਾਰ ਕਰਦਾ ਹੈ ਜਾਂ ਰੈਫਰੀ ਦੇ ਮੱਤ ਅਨੁਸਾਰ ਹਰਡਲਾਂ ਨੂੰ ਜਾਣ ਬੁੱਝ ਕੇ ਹੱਥਾਂ ਪੈਰਾਂ ਰਾਹੀਂ ਡੇਗਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਵੀ ਅਯੋਗ ਘੋਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
• ਜੇਕਰ ਉੱਪਰਲੇ ਨਿਯਮ ਤੋਂ ਉਪਰੰਤ ਹਰਡਲਾਂ ਡਿਗਦੀਆਂ ਹਨ, ਤਾਂ ਖਿਡਾਰੀ ਅਯੋਗ ਘੋਸ਼ਿਤ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
• ਜੇਕਰ ਕਿਸੇ ਖਿਡਾਰੀ ਨੇ ਜਾਣ-ਬੁੱਝ ਕੇ ਦੂਸਰੇ ਖਿਡਾਰੀ ਨੂੰ ਰੁਕਾਵਟ ਪਾਈ ਹੈ, ਤਾਂ ਰੈਫਰੀ ਉਸ ਦੌੜ ਨੂੰ ਦੁਬਾਰਾ ਕਰਾ ਦਿੰਦਾ ਹੈ ।
• ਜੇਕਰ Throw events ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲਿਆਂ ਦੀ ਗਿਣਤੀ ਬਹੁਤ ਹੀ ਹੋ ਜਾਵੇ ਤਾਂ ਰੈਫਰੀ ਨਿਰਧਾਰਿਤ ਥਾਂ (Qualifying marks) ਰੱਖ ਦਿੰਦਾ ਹੈ ਅਤੇ ਅੰਤ ਵਿਚ 6 ਚਾਂਸ ਦੇ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ ।
• ਜੇਕਰ ਦੌੜਾਕ ਸਾਰੀਆਂ ਹਰਡਲਾਂ ਪੈਰਾਂ ਰਾਹੀਂ ਸੁੱਟਦਾ ਜਾਂਦਾ ਹੈ, ਹੱਥਾਂ ਨਾਲ ਨਹੀਂ, ਤਾਂ ਦੌੜਾਕ ਨੂੰ ਅਯੋਗ ਘੋਸ਼ਿਤ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ ।
• ਕੋਈ ਐਥਲੀਟ ਦੋ ਵਾਰੀ ਫਾਊਲ ਸਟਾਰਟ ਲੈਂਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਰੇਸ ਵਿਚੋਂ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਡੈਕਥਲੋਨ (Decathlon)
ਮਰਦਾਂ ਲਈ ਡੈਕਥਲੋਨ ਵਿਚ ਦਸ ਈਵੈਂਟਸ ਹੁੰਦੇ ਹਨ ਜੋ ਕਿ ਐਥਲੀਟ ਨੇ ਦੋ ਦਿਨਾਂ ਵਿਚ ਕਰਨੇ ਹੁੰਦੇ ਹਨ ।

ਪਹਿਲੇ ਦਿਨ ਦੇ ਈਵੈਂਟਸ	ਦੂਜੇ ਦਿਨ ਦੇ ਈਵੈਂਟਸ
100 ਮੀਟਰ ਦੌੜ	110 ਮੀਟਰ ਹਰਡਲਜ਼
ਪਹਿਲੇ ਦਿਨ ਦੇ ਈਵੈਂਟਸ	ਦੂਜੇ ਦਿਨ ਦੇ ਈਵੈਂਟਸ
ਲੰਬੀ ਛਾਲ	ਡਿਸਕਸ ਥਰੋ
ਸ਼ਾਟ-ਪਟ	ਪੋਲ ਵਾਲਟ
ਹਾਈ ਜੰਪ	ਜੈਵਲਿਨ ਥਰੋ
400 ਮੀਟਰ ਦੌੜ	1500 ਮੀਟਰ ਦੌੜ

ਹੈਪਟਾਥਲੋਨ (Hepatathalon)
ਔਰਤਾਂ ਲਈ ਹੈਪਟਾਥਲੋਨ ਵਿਚ ਸੱਤ ਈਵੈਂਟਸ ਹੁੰਦੇ ਹਨ ਜੋ ਕਿ ਐਥਲੀਟ ਨੇ ਦੋ ਦਿਨਾਂ ਵਿਚ ਕਰਨੇ ਹੁੰਦੇ ਹਨ ।

ਪਹਿਲੇ ਦਿਨ ਦੇ ਈਵੈਂਟਸ	ਦੂਜੇ ਦਿਨ ਦੇ ਈਵੈਂਟਸ
1.100 ਮੀਟਰ ਹਰਡਲਜ਼	1.200 ਮੀਟਰ ਦੌੜ
2. ਲੰਬੀ ਛਾਲ	2. ਜੈਵਲਿਨ ਥਰੋ ।

ਪ੍ਰਸ਼ਨ 3.
ਮਰਦਾਂ ਅਤੇ ਇਸਤਰੀਆਂ ਲਈ ਐਥਲੈਟਿਕ ਈਵੈਂਟਸ ਦਾ ਵੇਰਵਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਮਰਦਾਂ ਲਈ ਫੀਲਡ ਈਵੈਂਟਸ ਵਿਚ ਲੰਮੀ ਛਲਾਂਗ, ਉੱਚੀ ਛਲਾਂਗ, ਤੀਸਰੀ ਛਲਾਂਗ ਅਤੇ ਪੋਲ ਵਾਲਟ ਆਉਂਦੇ ਹਨ । ਇਸਤਰੀਆਂ ਲਈ ਲੰਬੀ ਛਲਾਂਗ ਅਤੇ ਉੱਚੀ ਛਲਾਂਗ ਹੁੰਦੀ ਹੈ । ਥਰੋਇੰਗ ਈਵੈਂਟਸ ਵਿਚ ਮਰਦਾਂ ਲਈ ਸ਼ਾਟਪੁਟ, ਡਿਸਕਸ ਥਰੋ, ਜੈਵਲਿਨ ਥਰੋ ਅਤੇ ਹੈਮਰ ਥਰੋ ਆਉਂਦੇ ਹਨ । ਇਸਤਰੀਆਂ ਲਈ ਕੇਵਲ ਹੈਮਰ ਥਰੋ ਨਹੀਂ ਹੁੰਦੀ ।

ਮਰਦਾਂ ਲਈ ਪੈਂਟਾਥਲੈਨ ਵਿਚ ਪੰਜ ਈਵੈਂਟਸ ਹੁੰਦੇ ਹਨ –

• ਲੰਬੀ ਛਲਾਂਗ (Long Jump)
• ਜੈਵਲਿਨ ਥਰੋ (Javlin Throw)
• ਡਿਸਕਸ ਥਰੋ (Discus Throw)
• 200 ਮੀਟਰ ਦੌੜ (200 M. Race)
• 1500 ਮੀਟਰ ਦੌੜ (1500 M. Race) |

ਡੈਕੇਥਲੋਟਨ ਵਿਚ ਹੇਠ ਲਿਖੇ ਦਸ ਈਵੈਂਟਸ ਹੁੰਦੇ ਹਨ, ਜੋ ਕਿ ਦੋ ਦਿਨਾਂ ਵਿਚ ਐਥਲੀਟ ਨੇ ਕਰਨੇ ਹੁੰਦੇ ਹਨ । ਪਹਿਲੇ ਦਿਨ 100 ਮੀਟਰ ਰੇਸ, ਲੰਬੀ ਛਲਾਂਗ, ਸ਼ਾਟ-ਪੁਟ, ਉੱਚੀ ਛਲਾਂਗ ਅਤੇ 400 ਮੀਟਰ ਰੇਸ ਲਾਉਣੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਦੂਸਰੇ ਦਿਨ 110 ਮੀਟਰ ਹਰਡਲ ਰੇਸ, ਡਿਸਕਸ ਥਰੋ, ਪੋਲ ਵਾਲਟ, ਜੈਵਲਿਨ ਥਰੋ ਅਤੇ 1500 ਮੀਟਰ ਰੇਸ ਲਾਉਣੀ ਹੁੰਦੀ ਹੈ । ਇਸਤਰੀ ਲਈ ਹੈਪਟਾਥਲੋਨ ਦੋ ਦਿਨਾਂ ਵਿਚ ਕਰਨੀ ਹੁੰਦੀ ਹੈ | ਪਹਿਲੇ ਦਿਨ 100 ਮੀਟਰ ਹਰਡਲ ਰੇਸ, ਸ਼ਾਟਪੁਟ ਅਤੇ ਉੱਚੀ ਛਲਾਂਗ । ਦੂਸਰੇ ਦਿਨ ਲੰਬੀ ਛਲਾਂਗ ਅਤੇ 800 ਮੀਟਰ ਰੇਸ ਹੁੰਦੀ ਹੈ । ਟਰੈਕ ਈਵੈਂਟਸ ਵਿਚ 100, 200, 400, 800 ਮੀਟਰ ਤਕ ਦੀਆਂ ਦੌੜਾਂ ਆਉਂਦੀਆਂ ਹਨ |

ਪ੍ਰਸ਼ਨ 4.
200 ਮੀਟਰ ਅਤੇ 400 ਮੀਟਰ ਦੇ ਟਰੈਕ ਦੀ ਚਿਤਰ ਸਮੇਤ ਬਣਤਰ ਲਿਖੋ |
ਉੱਤਰ-
200 ਮੀਟਰ ਦੇ ਟਰੈਕ ਦੀ ਬਣਤਰ (Track for 200 metre)-ਇਸ ਟਰੈਕ ਦੀ ਲੰਬਾਈ 94 ਮੀਟਰ ਅਤੇ ਚੌੜਾਈ 53 ਮੀਟਰ ਹੁੰਦੀ ਹੈ ।

ਟਰੈਕ ਦੀ ਕੁੱਲ ਦੁਰੀ = 200 ਮੀਟਰ
ਦਿਸ਼ਾਵਾਂ ਦੀ ਲੰਬਾਈ = 40 ਮੀਟਰ
ਦਿਸ਼ਾਵਾਂ ਰਾਹੀਂ ਰੋਕੀ ਗਈ ਦੁਰੀ = 40 x 2 = 80 ਮੀਟਰ
ਕੋਨਿਆਂ ਵਿਚ ਰੋਕੀ ਜਾਣ ਵਾਲੀ ਦੁਰੀ = 120 ਮੀਟਰ 400 ਮੀਟਰ ਟਰੈਕ ਦੀ ਬਣਤਰ (Track for 400 Metre)
ਅੱਠ ਲੇਨਾਂ ਵਾਲਾ ਘੱਟ ਤੋਂ ਘੱਟ ਮਾਪ = 174.92 m x 95.92 m
ਟਰੈਕ ਦੀ ਕੁੱਲ ਦੂਰੀ = 400 ਮੀਟਰ
ਸਿੱਧੀ ਲੰਬਾਈ = 79 ਮੀਟਰ
ਦੋਵੇਂ ਦਿਸ਼ਾਵਾਂ ਦੀ ਦੂਰੀ = 242 ਮੀਟਰ
ਵਿਆਸ = 242 ਮੀਟਰ
ਦੌੜਨ ਵਾਲੀ ਦੂਰੀ ਦਾ ਅਰਧ ਵਿਆਸ = 38.20 ਮੀਟਰ
ਮਾਰਕਿੰਗ ਅਰਧ ਵਿਆਸ = 38.20 ਮੀਟਰ ਸਰਪਟ ਦੌੜ (Sprinting

ਆਪ ਦੌੜ ਦੇ ਢੰਗ ਉੱਤੇ ਧਿਆਨ ਕੇਂਦਰਿਤ ਕਰਨ ਦੀ ਬਜਾਏ ਮੁਕਾਬਲੇ ਦੀਆਂ ਹਾਲਤਾਂ ਅਧੀਨ ਛੋਟੀ ਦੌੜ ਲਗਾ ਕੇ ਅਤੇ ਭਾਰੀ ਰੁਕਾਵਟਾਂ ਰਾਹੀਂ ਤਾਕਤ ਦਾ ਵਿਕਾਸ ਕਰਕੇ ਜ਼ਿਆਦਾ ਚੰਗੀਆਂ ਕਾਰਗੁਜ਼ਾਰੀਆਂ ਹਾਸਿਲ ਕਰ ਸਕਦੇ ਹੋ । ਸ਼ੁਰੂ ਕਰਨ ਦੀ ਤਕਨੀਕ ਤੋਂ ਇਲਾਵਾ ਕਦਮਾਂ ਦੀ ਦਰ ਅਤੇ ਕਦਮਾਂ ਦੀ ਲੰਬਾਈ ਦੌੜ ਦੇ ਮੁੱਖ ਪਹਿਲੂ ਹਨ । ਬਹੁਤੇ ਖਿਡਾਰੀ ਉੱਚੀ ਰਫਤਾਰ ਤੇ ਸਰਪਟ ਦੌੜਨ ਰਾਹੀਂ ਨਿਪੁੰਨਤਾ ਪ੍ਰਾਪਤ ਕਰਨੀ ਸਿੱਖਦੇ ਹਨ |

ਬਲਾਕਾਂ ਤੋਂ ਬਾਹਰ ਦੌੜਣ ਦੀ ਸਿਖਲਾਈ ਵਿਚ ਆਪਣਾ ਬਹੁਤ ਸਮਾਂ ਨਾ ਗਵਾਉ –
(i) ਰਫਤਾਰ ਦਾ ਵਿਕਾਸ ਕਰਨਾ-ਗੌਲਿੰਗ ਸਟਾਰਟ ਤੋਂ ਹਟ ਕੇ 10 ਗਜ਼ ਦੇ ਫਾਸਲੇ ‘ਤੇ ਛੋਟੀ ਦੌੜ ਦੌੜੇ ਅਤੇ ਸਮਾਂ ਦਰਜ ਕਰੋ । ਤੁਸੀਂ ਕਾਫੀ ਸਾਰੀਆਂ ਛੋਟੀਆਂ ਦੌੜਾਂ ਵੀ ਲਾ ਸਕਦੇ ਹੋ ।

(ii) ਲੈਗ ਐਕਸ਼ਨ-70 ਗਜ਼ ਦੇ ਰਸਤੇ ਨੂੰ ਸਾਫ ਕਰੋ । 15 ਗਜ਼ ਦੇ ਰੋਲਿੰਗ ਸਟਾਰਟ ਵਿਚੋਂ ਨਿਕਲ ਕੇ ਸਾਫ ਕੀਤੇ ਹੋਏ ਰਸਤੇ (Track) ਉੱਤੇ ਸਰਪਟ ਦੌੜ ਦੌੜੇ । ਪੈਰਾਂ ਦੇ ਨਿਸ਼ਾਨਾਂ ਦੀ ਜਾਂਚ ਕਰੋ । ਤੁਸੀਂ ਵੇਖੋਗੇ ਕਿ ਕਦਮਾਂ ਦੀ ਲੰਬਾਈ ਵਧਦੀ-ਵਧਦੀ ਫਿਰ ਇਕ ਨਿਸ਼ਚਿਤ ਲੰਬਾਈ ਤੇ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ ।

(iii) ਕਦਮਾਂ ਦੀ ਲੰਬਾਈ ਅਤੇ ਲੱਤਾਂ ਦੀ ਰਫਤਾਰ ਦੋਵੇਂ ਪ੍ਰਸਪਰ ਸੰਬੰਧਿਤ ਹਿੱਸੇ ਹਨ ਅਤੇ ਮੁੱਖ ਤੌਰ ਤੇ ਇਨ੍ਹਾਂ ਦਾ ਨਿਰਣਾ ਲੱਤਾਂ ਦੀ ਲੰਬਾਈ, ਕੂਲ਼ੇ ਦੁਆਲੇ ਗਤੀਸ਼ੀਲਤਾ ਅਤੇ ਤਾਕਤ ਰਾਹੀਂ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਜੇ ਤੁਸੀਂ ਕੂਲੇ ਦੀ ਗਤੀਸ਼ੀਲਤਾ ਅਤੇ ਤਾਕਤ ਨੂੰ ਸਿਖਲਾਈ ਰਾਹੀਂ ਵਧਾਉਂਦੇ ਹੋ ਅਤੇ ਰੇਖਾ ਵਿਚ ਦੌੜ ਨੂੰ ਸਥਿਰ ਰੱਖਦੇ ਹੋ ਤਾਂ ਤੁਸੀਂ ਆਪਣੇ ਕਦਮਾਂ ਦੀ ਲੰਬਾਈ ਕੁੱਝ ਹੱਦ ਤਕ, ਪਰ ਇਕ ਮਹੱਤਵਪੂਰਨ ਹੱਦ ਤਕ ਵਧਾ ਸਕਣ ਦੀ ਆਸ ਕਰ ਸਕਦੇ ਹੋ । ਹੇਠ ਲਿਖੇ ਤਰੀਕੇ ਸਮਰੱਥ ਹੋ ਸਕਦੇ ਹਨ

(iv) ਬਾਹਵਾਂ ਦੀ ਕਾਰਵਾਈ-ਛੋਟੀ ਦੌੜ ਵਿਚ ਬਾਹਵਾਂ ਦੀ ਕਾਰਵਾਈ ਸਰੀਰ ਨੂੰ ਕਾਰਜਸ਼ੀਲ ਰੱਖਣ ਲਈ ਬੜੀ ਜ਼ਰੂਰੀ ਹੈ | ਬਾਂਹ ਨੂੰ 90° ਤੇ ਘੁੰਮਾਉਂਦਿਆਂ ਅੱਗੇ ਵੱਲ ਇਕ ਤਕੜੀ | ਹਿਲਜੁਲ ਨਾਲ ਸਰੀਰ ਦੇ ਅੱਗੇ ਪਿੱਛੇ ਕਰਨਾ ਦੌੜਾਕਾਂ ਲਈ ਆਮ ਗੱਲ ਹੈ | ਬਾਂਹ ਨੂੰ ਬਦਨ
ਦੇ ਪਿੱਛੇ ਲਿਆਉਂਦਿਆਂ ਪਹਿਲਾਂ ਖੋਲ੍ਹਣਾ ਅਤੇ ਫਿਰ ਕੁਹਣੀ ਦੇ ਕੋਣ ਤੇ ਮੋੜਨਾ ਚਾਹੀਦਾ ਹੈ, | ਪਰ ਇਹ ਗੱਲ ਲੱਤ ਦੀ ਚਾਲ ਨਾਲ ਵਕਤ ਨਾਲ ਤਾਲਮੇਲ ਵਿਚ ਕੁਦਰਤੀ ਹੀ ਪੈਦਾ ਹੋ ਜਾਂਦੀ ਹੈ ।

(v) ਸ਼ੁਰੂਆਤ-ਅਗਲੇ ਪੈਰ ਦੀ ਚਾਲ ਚਿੱਤਰ 3 ਅਤੇ 4 ਵਿਚ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ ਅਤੇ ਇਹ ਇਕ ਨਿਪੁੰਨ ਸ਼ੁਰੁਆਤ ਦੀ ਇਕ ਮੁੱਖ ਗੱਲ ਹੈ 1 ਬਲਾਕਾਂ ਦਾ ਰੱਖਣਾ ਤੁਹਾਡੀਆਂ ਲੱਤਾਂ ਤੇ ਬਾਹਵਾਂ ਦੀ ਲੰਬਾਈ ਅਤੇ ਕਿਸੇ ਹੱਦ ਤਕ ਤੁਹਾਡੀ ਤਾਕਤ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ | ਆਪਣੇ ਬਲਾਕਾਂ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਜਮਾਉ ਕਿ ਮੁਹਰਲਾ ਬਲਾਕ ਰੇਖਾ ਤੋਂ 18 ਇੰਚ ਪਿੱਛੋਂ ਅਤੇ ਪਿਛਲਾ ਰੇਖਾ ਤੋਂ ਲਗਪਗ 36 ਇੰਚ ‘ਤੇ ਹੋਵੇ । ਹੁਣ ਇਹਨਾਂ ਫਾਸਲਿਆਂ ਨਾਲ ਉਦੋਂ ਤਕ ਤਜਰਬਾ ਕਰੋ ਜਦੋਂ ਤਕ ਕਿ ਤੁਸੀਂ ਆਪਣੇ ਬਦਨ ਅਤੇ ਤਾਕਤ ਲਈ ਉੱਤਮ ਦਰ ਕਾਇਮ ਨਹੀਂ ਕਰ ਲੈਂਦੇ । (ਚਿੱਤਰ-2) ਦੀ ਸਥਿਤੀ ਵਿਚ ਬਦਨ ਅੱਗੇ ਵੱਲ ਇੰਝ ਝੁਕਾਉ ਕਿ ਬਹੁਤਾ ਭਾਰ ਬਾਹਵਾਂ ਉੱਤੇ ਆ ਜਾਵੇ ਅਤੇ ਕੂਲੇ ਉੱਪਰ ਉੱਠੇ ਹੋਏ ਮੋਢਿਆਂ ਤੋਂ ਉੱਚੇ ਹੋਣ ।

ਇਹ ਗੱਲ ਯਾਦ ਰੱਖੋ ਕਿ ਮੁਹਰਲੇ ਗੋਡੇ ਦਾ ਕੋਣ ਲਗਪਗ 90° ਹੈ । ਇਸ ਹਾਲਤ ਵਿਚ ਮੁਹਰਲੇ ਬਲਾਕ ਦਾ ਫੇਸ 60° ਕੋਣ ਤੇ ਹੈ ਅਤੇ ਪਿਛਲੇ ਬਲਾਕ ਦਾ ਲੰਬਾਤਮਕ ਰੂਪ ਵਿਚ । ਮੋਢਿਆਂ ਨੂੰ ਜਿੰਨਾ ਸੰਭਵ ਹੋ ਸਕੇ ਓਨਾ ਉੱਚੇ ਚੁੱਕੋ : ਬਾਹਵਾਂ ਦੀ ਵਾਧੂ ਲੰਬਾਈ ਹਰੇਕ ਹੱਥ ਨੂੰ ਸਿੱਧਾ ਕਰ ਕੇ ਵਧਾਉ | ਸਿਖਲਾਈ-ਛੋਟੀ ਦੌੜ ਦੀ ਮਜ਼ਬੂਤੀ, ਟੈਕ ਉੱਤੇ ਦੌੜਨ ਦੀ ਪੂਰੀ ਰਫ਼ਤਾਰ ਨਾਲ ਦੌੜਨ ਦੀ ਆਪਣੀ ਤਾਕਤ ਦੀ ਵਰਤੋਂ ਕਰਨ ਦੀ ਸਿਖਲਾਈ ਲੈ ਕੇ ਤੁਸੀਂ ਹਾਸਿਲ ਕਰ ਸਕਦੇ ਹੋ । ਤੁਸੀਂ ਹੇਠ ਲਿਖੀ ਉਦਾਹਰਨ ਅਨੁਸਾਰ ਰੋਜ਼ਾਨਾ ਦੀ ਸੂਚੀ ਬਣਾ ਸਕਦੇ ਹੋ । 1 x 180 ਗਜ਼ ਦੇ ਆਰਾਮ ਵਕਫਿਆਂ ਨਾਲ 6 x 70 ਗਜ਼ ਦਾ ਇਕ ਰੋਲਿੰਗ ਸਟਾਰਟ ਬਣਾਉ ! ਜਦੋਂ ਤੁਸੀਂ ਇਸ ਕੰਮ ਦੇ ਆਦੀ ਹੋ ਜਾਉਗੇ, ਤਾਂ ਇਸ ਨੂੰ ਪੰਜ ਮਿੰਟਾਂ ਦੇ ਆਰਾਮ ਤੋਂ ਬਾਅਦ ਦੁਹਰਾਉ । ਜਦੋਂ ਤੁਸੀਂ ਬਿਲਕੁਲ ਠੀਕ ਹੋ, ਤਾਂ ਇਸ ਸੂਚੀ ਨੂੰ ਤਿੰਨ ਵਾਰ ਦੁਹਰਾਉ ।

ਇਸ ਤੋਂ ਤੁਸੀਂ ਆਰਾਮ ਵਕਫਿਆਂ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਘੱਟ ਕਰਕੇ ਕੰਮ ਦੇ ਭਾਰ ਨੂੰ ਵਧਾ ਸਕਦੇ ਹੋ । ਜਦੋਂ ਤੁਸੀਂ ਇਕ ਪਿਸਤੌਲ ਦੀ ਵਰਤੋਂ ਕਰਦਿਆਂ ਇਕ ਸਮਰੱਥ ਸਟਾਰਟਰ ਨਾਲ ਟੋਲੇ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹੋ ਤਾਂ ਛੋਟੀ ਦੌੜ ਦੇ ਸ਼ੁਰੂ ਕਰਨ ਦੀ ਸਿਖਲਾਈ ਬਹੁਤ ਕੀਮਤੀ ਹੈ । ਕੁੱਝ ਲਾਭਕਾਰੀ ਕੰਮ ਆਲੋਚਕਾਂ ਦੀ ਵਰਤੋਂ ਨਾਲ ਵੀ ਕੀਤਾ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ, ਪਰ ਹਰੇਕ ਦੌੜਾਕ ਨੂੰ ਆਪਣੀ ਸ਼ੁਰੂਆਤ ਸੰਭਵ ਵਧੀਆ ਹਾਲਤਾਂ ਅਧੀਨ ਕਰਨ ਲਈ ਦ੍ਰਿੜ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਆਪਣੀ ਸਿਖਲਾਈ ਲਈ ਇਸ ਕਿਸਮ ਦੀ ਮਿਆਦ ਕਾਇਮ ਕਰੋ । ਥੋੜੇ ਨਾਲ ਹੀ ਸੰਤੁਸ਼ਟ ਨਾ ਹੋਵੇ । ਦੌੜਾਕ ਵਾਸਤੇ ਪੂਰੇ ਬਦਨ ਲਈ ਅਤੇ ਵਿਸ਼ੇਸ਼ ਕਰਕੇ ਬਾਹਵਾਂ, ਮੋਢਿਆਂ ਅਤੇ ਲੱਤਾਂ ਲਈ ਭਾਰੀ ਰੁਕਾਵਟਾਂ ਦੀ ਸਿਖਲਾਈ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ | ਇਕ ਹਫਤੇ ਵਿਚ ਇਸ ਬਾਰੇ ਘੱਟੋਘੱਟ 40 ਮਿੰਟਾਂ ਦੇ ਦੋ ਅਭਿਆਸ ਲਾਜ਼ਮੀ ਹਨ ।

TRACK EVENTS OF RACES SHORT, MIDDLE & LONG ਸਟਿੰਗ (Sprinting)-ਪ੍ਰਿੰਟਿੰਗ ਉਹ ਦੌੜ ਹੁੰਦੀ ਹੈ, ਜੋ ਅਕਸਰ ਪੂਰੀ ਤਾਕਤ ਅਤੇ ਪੂਰੀ ਗਤੀ ਨਾਲ ਦੌੜੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਵਿਚ 100 ਮੀਟਰ ਅਤੇ 200 ਮੀਟਰ ਦੀਆਂ ਦੌੜਾਂ ਆਉਂਦੀਆਂ ਹਨ । ਅੱਜ-ਕਲ੍ਹ ਤਾਂ 400 ਮੀਟਰ ਦੌੜ ਨੂੰ ਵੀ ਇਸ ਵਿਚ ਗਿਣਿਆ ਜਾਣ ਲੱਗਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਨਾਲ ਦੌੜਾਂ ਵਿਚ ਪ੍ਰਤੀਕਿਰਿਆ (Reaction) ਟਾਈਮ ਅਤੇ Speed ਦਾ ਬੜਾ ਮਹੱਤਵ ਹੈ ।

(i) ਸਟਾਰਟ (Starts-ਛੋਟੇ ਫਾਸਲੇ ਦੀਆਂ ਰੇਸਾਂ ਵਿਚ ਅਕਸਰ ਹੇਠ ਦਿੱਤੇ ਤਿੰਨ ਤਰ੍ਹਾਂ ਦੇ ਸਟਾਰਟ ਲਏ ਜਾਂਦੇ ਹਨ –

1. ਬੰਚ ਸਟਾਰਟ (Bunch Stat)
2. ਮੀਡੀਅਮ ਸਟਾਰਟ (Medium Start)
3. ਅਲੈੱਗੇਟੇਡ ਸਟਾਰਟ (Elorgated Start)

1. ਬੰਚ ਸਟਾਰਟ (Bunch Star)- ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਸਟਾਰਟ ਵਾਸਤੇ ਬਲਾਕਾਂ ਵਿਚਕਾਰ ਫਾਸਲਾ 8 ਤੋਂ 19 ਇੰਚ ਦਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਅੱਗੇ ਵਾਲਾ ਬਲਾਕ ਸਟਾਰਟਿੰਗ ਲਾਈਨ ਤੋਂ ਤਕਰੀਬਨ 19 ਇੰਚ ਦੇ ਕਰੀਬ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਐਥਲੀਟ ਇਸ ਤਰ੍ਹਾਂ ਬਲਾਕ ਵਿਚ ਅੱਗੇ ਨੂੰ ਝੁਕਦਾ ਹੈ ਕਿ ਪਿਛਲੇ ਪੈਰ ਦੀ ਟੋ ਅਤੇ ਅਗਲੇ ਪੈਰ ਦੀ ਅੱਡੀ ਇਕ ਦੂਸਰੇ ਦੇ ਸਮਾਨ ਸਥਿਤ ਹੋਣ ਤੋਂ ਹੱਥ ਸਟਾਰਟਿੰਗ ਲਾਈਨ ਤੇ ਬਿਜ ਬਣਾਏ ਹੋਏ ਅਤੇ ਸਟਾਰਟਿੰਗ ਲਾਈਨ ਤੋਂ ਪਿੱਛੇ ਹੋਣ । ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਸਟਾਰਟ ਵਿਚ ਜਿਉਂ ਹੀ ਸੈੱਟ ਪੋਜ਼ੀਸ਼ਨ (Set Position) ਦਾ ਹੁਕਮ ਹੁੰਦਾ ਹੈ, Hips ਨੂੰ ਉੱਪਰ ਲਿਜਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਸਟਾਰਟ ਸਭ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਅਸਥਿਰ ਹੁੰਦਾ ਹੈ |

2. ਮੀਡੀਅਮ ਸਟਾਰਟ (Medium Start)-ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਸਟਾਰਟ ਵਿਚ ਬਲਾਕਾਂ ਵਿਚਕਾਰ ਫਾਸਲਾ 10 ਤੋਂ 13 ਇੰਚ ਵਿਚਕਾਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਸਟਾਰਟਿੰਗ ਲਾਈਨ ਤੋਂ ਪਹਿਲੇ ਬਲਾਕ ਦਾ ਫਾਸਲਾ ਤਕਰੀਬਨ 15 ਇੰਚ ਦੇ ਵਿਚਕਾਰ ਹੁੰਦਾ ਹੈ । ਅਕਸਰ ਐਥਲੀਟ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਸਟਾਰਟ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹਨ । ਜਿਸ ਵਿਚ ਪਿਛਲੇ ਪੈਰ ਦਾ ਗੋਡਾ ਅਗਲੇ ਪੈਰ ਦਾ ਵਿਚਕਾਰ ਵਾਲਾ ਭਾਰਾ ਇਕ ਸੇਧ ਵਿਚ ਹੁੰਦੇ ਹਨ ਅਤੇ Set Position ਤੋਂ His ੜੇ ਮੋਢੇ ਤਕਰੀਬਨ ਇੱਕੋ ਜਿਹੀ ਉੱਚਾਈ ਤੇ ਹੁੰਦੇ ਹਨ ।

3. ਅਲੈੱਗੇਟੇਡ ਸਟਾਰਟ (Elongated Start)-ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਸਟਾਰਟ ਬਹੁਤ ਘੱਟ ਲੋਕ ਲੈਂਦੇ ਹਨ । ਇਸ ਵਿਚ ਬਲਾਕਾਂ ਸਟਾਰਟਿੰਗ ਬਲਾਕ (Starting Block) ਵਿਚਕਾਰ ਫਾਸਲਾ 25 ਤੋਂ 28 ਇੰਚ ਵਿਚਕਾਰ ਹੁੰਦਾ ਹੈ : ਪਿਛਲੇ ਪੈਰ ਦਾ ਗੋਡਾ ਤਕਰੀਬਨ ਅਗਲੇ ਪੈਰ ਦੀ ਅੱਡੀ ਦੇ ਸਾਹਮਣੇ ਹੁੰਦਾ ਹੈ |

ਸਟਾਰਟ ਲੈਣਾ (Start)-ਜਦੋਂ ਕਿਸੇ ਵੀ ਰੇਸ ਲਈ ਸਟਾਰਟ ਲਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਤਿੰਨ ਤਰ੍ਹਾਂ ਦੇ ਆਦੇਸ਼ਾਂ ਤੇ ਕੰਮ ਕਰਨਾ ਪੈਂਦਾ ਹੈ-

1. ਆਨ ਯੂਅਰ ਮਾਰਕ (On your mark)
2. ਸੈਂਟ ਪੋਜ਼ੀਸ਼ਨ (Set Position)
3. ਪਿਸਤੌਲ ਦੀ ਆਵਾਜ਼ ‘ਤੇ ਜਾਣਾ (Co)

ਰੇਸ ਦਾ ਅੰਤ (Finish of the Race) -ਰੋਸ ਦਾ ਅੰਤ ਬਹੁਤ ਹੀ ਮਹੱਤਵਪੂਰਨ ਹੁੰਦਾ ਹੈ । ਆਮ ਕਰ ਕੇ ਖਿਡਾਰੀ ਤਿੰਨ ਤਰ੍ਹਾਂ ਨਾਲ ਰੇਸ ਨੂੰ ਖ਼ਤਮ ਕਰਦੇ ਹਨ । ਇਹ ਤਰੀਕੇ ਹਨ

1. ਭੁੱਜ ਕੇ ਸਿੱਧੇ ਅੱਗੇ ਨਿਕਲ ਜਾਣਾ (Runt througla)
2. ਅੱਗੇ ਨੂੰ ਝੁਕਣਾ (Lunge)
3. ਮੋਢਾ ਅੱਗੇ ਕਰਨਾ (The Shoulders String)

ਦਰਮਿਆਨੇ ਫ਼ਾਸਲੇ ਦੀਆਂ ਰੇਸਾਂ (Middle Distanc Races)-ਟੈਕ ਈਵੈਂਟਾਂ ਵਿਚ ਕੁੱਝ ਰੇਸਾਂ ਦਰਮਿਆਨੇ ਫ਼ਾਸਲੇ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਆਮ ਕਰਕੇ ਉਹ ਰੇਸਾਂ ਜਿਹੜੀਆਂ 400 ਗਜ਼ ਤੋਂ ਉੱਪਰ ਅਤੇ 100 ਗਜ਼ ਤੋਂ ਥੱਲੇ ਹੁੰਦੀਆਂ ਹਨ, ਉਨ੍ਹਾਂ ਨੂੰ ਇਸ ਸ਼੍ਰੇਣੀ ਵਿਚ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਰੇਸਾਂ 400 ਮੀਟਰ ਅਤੇ 800 ਮੀਟਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ? ਇਨ੍ਹਾਂ ਰੇਸਾਂ ਵਿਚ ਰਫ਼ਤਾਰ ਅਤੇ ਸਹਿਨਸ਼ੀਲਤਾ ਦੋਹਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਹੀ ਐਥਲੀਟ ਇਨ੍ਹਾਂ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਕਾਮਯਾਬ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਕੋਲ ਇਹ ਦੋਵੇਂ ਚੀਜ਼ਾਂ ਦ ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਰੇਸਾਂ ਵਿਚ ਆਮ ਕਰਕੇ ਇੱਕੋ ਦੀ ਰਫਤਾਰ ਰੱਖੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਅੰਤ ਵਿਚ ਪੂਰਾ ਜ਼ੋਰ ਲਗਾ ਕੇ ਫੇਸ ਨੂੰ ਜਿੱਤਿਆ ਜਾਂਦਾ ਹੈ | 400 ਸੰਟਰ ਦਾ ਸਰਟ ਤਾਂ ਸਪ੍ਰਿੰਟਿੰਗ ਦੀ ਤਰ੍ਹਾਂ ਹੀ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਕਿ 800 ਮੀਟਰ ਦਾ ਸਟਾਰਟ ਸਿਰਫ ਖੜੇ ਹੋ ਕੇ ਹੀ ਲਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਜਿੱਥੋਂ ਤਕ ਹੋ ਸਕੇ ਇਸ ਰੇਸ ਵਿਚ ਕਦਮ (Strides) ਵੱਡੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।

ਲੰਬੇ ਫ਼ਾਸਲੇ ਦੀਆਂ ਰੇਸਾਂ (Long Distance Races)-ਲੰਬੇ ਫ਼ਾਸਲੇ ਦੀਆਂ ਰੇਸਾਂ, . ਜਿਵੇਂ ਕਿ ਨਾਂ ਤੋਂ ਹੀ ਪਤਾ ਚੱਲਦਾ ਹੈ, ਫ਼ਾਸਲਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਅਕਸਰ ਇਹ ਰੇਸਾਂ ਮੀਲ ਤੋਂ ਉੱਪਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । 1500 ਮੀਟਰ, 3, 000 ਮੀਟਰ, 5,000 ਮੀਟਰ ਆਦਿ ਰੇਸਾਂ ਲੰਬੇ ਫਾਸਲੇ ਦੀਆਂ ਰੇਸਾਂ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚ ਐਥਲੀਟ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (endurance) ਦਾ ਜ਼ਿਆਦਾ ਯੋਗਦਾਨ ਹੈ । ਲੰਬੇ ਫ਼ਾਸਲੇ ਦੀਆਂ ਰੇਸਾਂ ਵਿਚ ਐਥਲੀਟ ਨੂੰ ਆਪਣੀ ਸ਼ਕਤੀ ਅਤੇ ਸਮਰੱਥਾ ਦਾ ਇਸਤੇਮਾਲ ਯੋਜਨਾਬੱਧ ਤਰੀਕੇ ਅਨੁਸਾਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਜਿਹੜੇ ਐਥਲੀਟ ਇਸ ਕਲਾ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰ ਜਾਂਦੇ ਹਨ, ਉਹ ਲੰਬੇ ਫ਼ਾਸਲੇ ਦੀਆਂ ਰੇਸਾਂ ਵਿਚ ਕਾਮਯਾਬ ਹੋ ਜਾਂਦੇ ਹਨ ।

ਇਸ ਤਰ੍ਹਾਂ ਦੀਆਂ ਰੇਸਾਂ ਦੇ ਆਰੰਭ ਨੂੰ ਛੱਡ ਕੇ ਸਾਰੀ ਰੇਸ ਵਿਚ ਐਥਲੀਟ ਦਾ ਸਰੀਰ ਸਿੱਧਾ ਅਤੇ ਅੱਗੇ ਵਲ ਥੋੜਾ ਝੁਕਿਆ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਸਿਰ ਸਿੱਧਾ ਰੱਖਦੇ ਹੋਏ ਧਿਆਨ ਟਰੈਕ ਵਲ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਬਾਹਵਾਂ ਢਿੱਲੀਆਂ ਜਿਹੜੀਆਂ ਅੱਗੇ ਵਲ ਨੂੰ ਲਟਕਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ, ਜਦ ਕਿ ਕੂਹਣੀਆਂ ਕੋਲੋਂ ਬਾਹਵਾਂ ਮੁੜੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਹੱਥ ਬਿਨਾਂ ਕਿਸੇ ਤਣਾਅ ਦੇ ਥੋੜੇ ਜਿਹੇ ਬੰਦ ਹੁੰਦੇ ਹਨ । ਬਾਹਵਾਂ ਅਤੇ ਲੱਤਾਂ ਦੇ Action ਜਿੱਥੋਂ ਤਕ ਹੋ ਸਕਣ, ਬਿਨਾਂ ਕਿਸੇ ਜ਼ਿਆਦਾ ਸ਼ਕਤੀ ਅਤੇ ਕੋਸ਼ਿਸ਼ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਦੌੜਨ ਸਮੇਂ ਪੈਰ ਦਾ ਅੱਗੇ ਵਾਲਾ ਹਿੱਸਾ ਧਰਤੀ ਉੱਤੇ ਆਉਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਅੱਡੀ ਵੀ ਗਰਾਊਂਡ ਨੂੰ ਛੂਹ ਜਾਂਦੀ ਹੈ, ਪਰੰਤੂ ਜ਼ਿਆਦਾ ਪੁਸ਼ (Push) ਟੋਅ ਤੋਂ ਹੀ ਲਈ ਜਾਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੀਆਂ ਰੇਸਾਂ ਵਿਚ ਕਦਮ (Strides) ਛੋਟੇ ਅਤੇ ਆਪਣੇ ਆਪ ਬਿਨਾਂ ਵਧਾਏ ਆਉਣੇ ਚਾਹੀਦੇ ਹਨ | ਸਾਰੀ ਰੇਸ ਵਿਚ ਸਰੀਰ ਬਹੁਤ Relax ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਹਰਡਲ ਦੌੜਾਂ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ –
100 ਮੀਟਰ ਹਰਡਲ ਦੌੜ
(100 METRE HURDLE RACE)
ਆਮ ਤੌਰ ਤੇ ਰੁਕਾਵਟ ਦੌੜ ਦੇ ਐਥਲੀਟ ਪਹਿਲੀ ਹਰਡਲ ਤਕ ਪੁੱਜਣ ਵਿਚ 8 ਕਦਮ ਲੈਂਦੇ ਹਨ । ਸਟਾਰਟਿੰਗ ਬਲਾਕ ਤੇ ਬੈਠਦੇ ਸਮੇਂ ਵਧੇਰੇ ਤਾਕਤ ਵਾਲੇ ਪੈਰ (Take off Foot) ਨੂੰ ਅੱਗੇ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਦੌੜਾਕ ਜੇ ਲੰਬਾ ਹੈ ਅਤੇ ਜ਼ਿਆਦਾ ਤੇਜ਼ ਭੱਜਣ ਦੀ ਯੋਗਤਾ ਰੱਖਦਾ ਹੈ ਤਾਂ ਉਸ ਹਾਲਤ ਵਿਚ ਇਹ ਫਾਸਲਾ ਉਹਦੇ ਲਈ ਘੱਟ ਸਕਦਾ ਹੈ । ਅਜਿਹੀ ਹਾਲਤ ਵਿਚ ਤਾਕਤਵਰ ਪੈਰ ਪਿਛਲੇ ਥਲ (ਬਲਾਕ) ਤੇ ਰੱਖ ਕੇ ਦੌੜਾਕ ਭੱਜੇਗਾ । ਇਸ ਲਈ ਤਾਕਤਵਰ ਪੈਰ ਹਰਡਲ ਤੋਂ ਲਗਪਗ 2 ਮੀਟਰ ਪਿੱਛੇ ਆਵੇਗਾ । ਸ਼ੁਰੂ ਵਿਚ ਦੌੜਾਕ ਨੂੰ ਤਿੰਨ ਤੋਂ ਪੰਜ ਕਦਮ ਤਕ ਆਪਣੀ ਨਜ਼ਰ ਹੇਠਾਂ ਰੱਖਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਬਾਅਦ ਵਿਚ ਹਰਡਲ ਤੇ ਹੀ ਨਜ਼ਰ ਕੇਂਦਰਿਤ ਰਹਿਣੀ ਚਾਹੀਦੀ ਹੈ । ਸ਼ੁਰੂ ਤੋਂ ਅਖੀਰ ਤਕ ਕਦਮਾਂ ਵਿਚਕਾਰ ਦਾ ਫਾਸਲਾ ਲਗਾਤਾਰ ਵਧਦਾ ਹੀ ਜਾਵੇਗਾ | ਪਰ ਆਖ਼ਰੀ ਕਦਮ ਉਛਾਲ ਕਦਮ ਨਾਲੋਂ ਲਗਪਗ 6 ਇੰਚ (10 ਸੈਂ:ਮੀ:) ਛੋਟਾ ਹੀ ਰਹੇਗਾ ।

ਆਮ ਦੌੜਾਂ ਦੀ ਤੁਲਨਾ ਵਿਚ ਹਰਡਲ ਦੌੜ ਵਿਚ ਭੱਜਦੇ ਸਮੇਂ ਦੌੜਾਕ ਦੇ ਗੋਡੇ ਵਧੇਰੇ ਉੱਪਰ ਆਉਣਗੇ ਅਤੇ ਜ਼ਮੀਨ ਤੇ ਪੂਰਾ ਨਾ ਰੱਖ ਕੇ ਸਿਰਫ ਪੈਰ ਦੇ ਅਗਲੇ ਹਿੱਸੇ ਪੰਜਿਆਂ ਨੂੰ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਹਰਡਲ ਨੂੰ ਪਾਰ ਕਰਦੇ ਸਮੇਂ ਉਛਾਲ ਪੈਰ ਨੂੰ ਸਿੱਧਾ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਅਗਲੇ ਪੈਰ ਨੂੰ ਗੋਡੇ ਤੋਂ ਉੱਪਰ ਚੁੱਕਣਾ ਚਾਹੀਦਾ ਹੈ । ਪੈਰ ਦਾ ਪੰਜਾ ਜ਼ਮੀਨ ਵੱਲ ਹੇਠਾਂ ਨੂੰ ਝੁਕਿਆ ਹੋਇਆ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਅਗਲੇ ਪੈਰ ਨੂੰ ਇੱਕੋ ਵੇਲੇ ਸਿੱਧਾ ਕਰਦੇ ਹੋਏ ਹਰਡਲ ਦੇ ਉੱਪਰ ਤੋਂ ਲੈ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਸਰੀਰ ਦਾ ਉੱਪਰ ਦਾ ਹਿੱਸਾ ਅੱਗੇ ਵਲ ਝੁਕਿਆ ਹੋਇਆ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਹਰਡਲ ਨੂੰ ਪਾਰ ਕਰਦੇ ਹੀ ਅਗਲੇ ਪੈਰ ਦੇ ਪੱਖ ਨੂੰ ਹੇਠਾਂ ਦਬਾਉਂਦੇ ਰਹਿਣਾ ਹੈ, ਜਿਸ ਨਾਲ ਹਰਡਲ ਪਾਰ ਕਰਨ ਦੇ ਬਾਅਦ ਪੰਜਾ ਹਰਡਲ ਤੋਂ ਵੱਧ ਫਾਸਲੇ ਤੇ ਨਾ ਪੈ ਕੇ ਉਸ ਦੇ ਕੋਲ ਹੀ ਜ਼ਮੀਨ ‘ਤੇ ਪਵੇ । ਉਸ ਦੇ ਨਾਲ ਹੀ ਪਿਛਲੇ ਪੈਰ ਨੂੰ ਗੋਡੇ ਨੂੰ ਝੁਕਾ ਕੇ ਹਰਡਲ ਦੇ ਉੱਪਰੋਂ ਜ਼ਮੀਨ ਦੇ ਸਮਨਾਂਤਰ ਰੱਖ ਕੇ ਗੋਡੇ ਨੂੰ ਸੀਨੇ ਦੇ ਕੋਲੋਂ ਅੱਗੇ ਲਿਆਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪੈਰ ਅੱਗੇ ਆਉਂਦੇ ਹੀ ਦੌੜਾਕ ਤੇਜ਼ ਭੱਜਣ ਲਈ ਤਿਆਰ ਰਹੇਗਾ | ਹਰਡਲ ਪਾਰ ਕਰਨ ਦੇ ਬਾਅਦ ਪਹਿਲਾ ਕਦਮ 1.55 ਤੋਂ 1.60 ਮੀਟਰ ਦੇ ਫਾਸਲੇ ‘ਤੇ, ਦੁਸਰਾ 2.10 ਮੀਟਰ ਦੇ ਅਤੇ ਤੀਸਰਾ ਲਗਪਗ 2.00 ਮੀਟਰ ਦੇ ਅੰਤਰ ‘ਤੇ ਪੈਣਾ ਚਾਹੀਦਾ ਹੈ । ( 12 ਮੀ:, 13.72.9 ਮੀ: 9.14 ਮੀ: 14.20 ਮੀ:)

ਪ੍ਰਸ਼ਨ 6.
ਵੱਖ-ਵੱਖ ਮੁਕਾਬਲਿਆਂ ਲਈ ਹਰਡਲਜ਼ ਦੀ ਗਿਣਤੀ, ਉਚਾਈ ਅਤੇ ਦੂਰੀ ਲਿਖੋ ।
ਉੱਤਰ-
ਵੱਖ-ਵੱਖ ਮੁਕਾਬਲਿਆਂ ਲਈ ਹਰਡਲਜ਼ ਦੀ ਗਿਣਤੀ, ਉਚਾਈ ਅਤੇ ਦੁਰੀ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-

400 ਮੀਟਰ ਹਰਡਲ ਮਰਦ ਅਤੇ ਔਰਤਾਂ)
(400 M. HURDLES-MEN AND WOMEN)

ਆਮ ਤੌਰ ਤੇ ਦੌੜਾਕ ਨੂੰ ਇਸ ਦੌੜ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਅਸੁਵਿਧਾ ਆਪਣੇ ਕਦਮਾਂ ਦੇ ਵਿਚਕਾਰ ਤਾਲਮੇਲ ਬਿਠਾਉਣ ਵਿਚ ਹੁੰਦੀ ਹੈ । ਸ਼ੁਰੂ ਵਿਚ ਪਹਿਲੀ ਹਰਡਲ ਦੇ ਵਿਚਕਾਰ ਦੀ ਦੂਰੀ ਨੂੰ ਲੋਕ ਆਮ ਤੌਰ ‘ਤੇ 21 ਤੋਂ 25 ਕਦਮਾਂ ਵਿਚ ਪੂਰੀ ਕਰ ਲੈਂਦੇ ਹਨ ਅਤੇ ਰੁਕਾਵਟ ਦੇ ਵਿਚਕਾਰ 13-15 ਜਾਂ 17 ਕਦਮ ਰੱਖਦੇ ਹਨ । ਕੁੱਝ ਦੌੜਾਕ ਸ਼ੁਰੂ ਵਿਚ 14 ਅਤੇ ਬਾਅਦ ਵਿਚ 16 ਕਦਮਾਂ ਵਿਚ ਇਸ ਦੂਰੀ ਨੂੰ ਪੂਰਾ ਕਰ ਲੈਂਦੇ ਹਨ । ਸੱਜੇ ਪੈਰ ਨਾਲ ਉਛਾਲ ਲੈਣ ਨਾਲ ਲਾਭ ਹੋਣ ਦੀ ਵਧੇਰੇ ਸੰਭਾਵਨਾ ਰਹਿੰਦੀ ਹੈ । ਆਮ ਤੌਰ ਤੇ ਉਛਾਲ 200 ਮੀਟਰ ਤੋਂ ਲਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਪਹਿਲਾ ਕਦਮ ਹਰਡਲ ਨੂੰ ਪਾਰ ਕਰ ਕੇ ਜ਼ਮੀਨ ‘ਤੇ ਪੈਂਦਾ ਹੈ, ਉਹ 1.20 ਮੀਟਰ ਦਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੀ ਤਕਨੀਕ 10 ਮੀਟਰ ਅਤੇ 100 ਮੀਟਰ ਹਰਡਲਾਂ ਵਰਗੀ ਹੀ ਹੁੰਦੀ ਹੈ । 400 ਮੀਟਰ ਦੌੜ ਦੇ ਸਮੇਂ ਤੋਂ ਸੈਕਿੰਡ 25 ਤੋਂ 3-5 ਤਕ 400 ਮੀਟਰ ਹਰਡਲ ਦਾ ਸਮਾਂ ਵੱਧ ਆਉਂਦਾ ਹੈ ।

ਹਰਡਲਜ਼
(HURDLES)
ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਰੇਸ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਵੇਲੇ ਸਰੀਰ ਅੰਦਰ ਇੰਨਾ ਬਲ (Stamina) ਅਤੇ ਰਫ਼ਤਾਰ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਕਿ ਐਥਲੀਟ ਆਪਣੀ ਰੇਸ ਨੂੰ ਤਕਰੀਬਨ ਫਿਨਿਸ਼ ਲਾਈਨ ਤੋਂ ਪੰਜ-ਸੱਤ ਗਜ਼ ਅੱਗੇ ਤਕ ਖ਼ਤਮ ਕਰਨ ਦਾ ਇਰਾਦਾ ਰੱਖੇ, ਤਾਂ ਹੀ ਚੰਗੇ ਨਤੀਜਿਆਂ ਦੀ ਆਸ ਰੱਖੀ ਜਾ ਸਕਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਫੀਲਡ ਈਵੈਂਟਸ ਵਿਚ ਕਿੰਨੇ ਈਵੈਂਟਸ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ –

1. ਰਨਵੇ ਦੀ ਲੰਬਾਈ = 40 ਮੀ. ਘੱਟੋ ਤੋਂ ਘੱਟ, 45 ਮੀ. ਵੱਧ ਤੋਂ ਵੱਧ
2. ਰਨਵੇ ਦੀ ਚੌੜਾਈ = 1.22 ਮੀ.
3. ਪਿਟ ਦੀ ਲੰਬਾਈ । = 10 ਮੀ.
4. ਪਿਟ ਦੀ ਚੌੜਾਈ = 2.75 ਮੀ. ਤੋਂ 3 ਮੀ.
5. ਟੇਕ ਆਫ਼ ਬੋਰਡ ਦੀ ਲੰਬਾਈ = 1.22 ਮੀ.
6. ਟੇਕ ਆਫ਼ ਬੋਰਡ ਦੀ ਚੌੜਾਈ = 20 ਸੈਂ.ਮੀ.
7. ਟੇਕ ਆਫ਼ ਬੋਰਡ ਦੀ ਗਹਿਰਾਈ = 10 ਸੈਂ.ਮੀ.

ਲੰਮੀ ਛਾਲ (LONG JUMP)

ਲੰਮੀ ਛਾਲ ਦਾ ਢੰਗ (Method of Long Jump)-ਛਾਲ ਲਾਉਣ ਵਾਲੇ ਪੈਰ ਨੂੰ ਪੱਕਾ ਕਰਨ ਲਈ ਲੰਮੀ ਛਾਲ ਵਿਚ ਵੀ ਉਸੇ ਤਰ੍ਹਾਂ ਨਾਲ ਕਰਾਂਗੇ ਜਿਵੇਂ ਕਿ ਉੱਚੀ ਛਾਲ ਵਿਚ ਕੀਤਾ ਗਿਆ ਸੀ | ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਛਾਲ ਮਾਰਨ ਵਾਲੇ ਪੈਰ ਨੂੰ ਅੱਗੇ ਸਿੱਧਾ ਰੱਖ ਕੇ ਅਤੇ ਸੁਤੰਤਰ ਪੈਰ ਨੂੰ ਅੱਗੇ ਅਤੇ ਸੱਜੇ ਪੈਰ ਨੂੰ ਪਿੱਛੇ ਰੱਖ ਕੇ ਸੱਜੇ ਗੋਡੇ ਤੋਂ ਝੁਕਾ ਕੇ ਉੱਪਰ ਵਲ ਲੈ ਜਾਣਗੇ ਅਤੇ ਇਸ ਦੇ ਨਾਲ ਹੀ ਸੱਜੇ ਹੱਥ ਨੂੰ ਕੁਹਣੀ ਤੋਂ ਝੁਕਾ ਕੇ ਰੱਖਾਂਗੇ । ਢੰਗ ਉਸੇ ਤਰ੍ਹਾਂ ਨਾਲ ਹੋਵੇਗਾ ਜਿਵੇਂ ਕਿ ਤੇਜ਼ ਦੌੜਨ ਵਾਲੇ ਕਰਦੇ ਹਨ । ਇਸ ਕਿਰਿਆ ਨੂੰ ਪਹਿਲਾਂ ਖੜੇ ਹੋ ਕੇ ਅਤੇ ਬਾਅਦ ਵਿਚ ਚਾਰ-ਪੰਜ ਕਦਮ ਤਰ ਕੇ ਕਰਾਂਗੇ । ਜਦੋਂ ਇਹ ਕਿਰਿਆ ਠੀਕ ਤਰ੍ਹਾਂ ਨਾਲ ਹੋਣ ਲੱਗੇ, ਤਦ ਥੋੜ੍ਹਾ ਭਜਦੇ ਹੋਏ ਇਹ ਕਿਰਿਆ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।

ਇਸ ਸਮੇਂ ਉੱਪਰ ਜਾਂਦੇ ਸਮੇਂ ਜ਼ਮੀਨ ਨੂੰ ਛੱਡ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ –
1. ਛੇ ਜਾਂ ਸੱਤ ਕਦਮ ਦੌੜ ਕੇ ਅੱਗੇ ਅਤੇ ਉੱਪਰ ਜਾ ਕੇ ਕੁੱਦਦਾ ਹੋਇਆ ਖਿਡਾਰੀ ਜ਼ਮੀਨ ਤੇ ਆਵੇਗਾ । ਇਸ ਕਿਰਿਆ ਨੂੰ ਕਈ ਵਾਰ ਦੁਹਰਾਉਣ ਤੋਂ ਬਾਅਦ ਜ਼ਮੀਨ ‘ਤੇ ਆਉਂਦੇ ਸਮੇਂ ਕੁੱਦਣ ਵਾਲੇ ਪੈਰ ਨੂੰ ਵੀ ਸੁਤੰਤਰ ਪੈਰ ਦੇ ਨਾਲ ਹੀ ਜ਼ਮੀਨ ਤੇ ਲੈ ਆਵੇਗਾ |
2. ਉੱਪਰ ਦੀ ਕਿਰਿਆ ਨੂੰ ਕਈ ਵਾਰ ਕਰਨ ਤੋਂ ਬਾਅਦ ਇਕ ਰੁਮਾਲ ਲੱਕੜੀ ਵਿਚ ਬੰਨ੍ਹ ਕੇ ਕੁੱਦਣ ਵਾਲੀ ਥਾਂ ਤੋਂ ਥੋੜ੍ਹੀ ਉੱਚਾਈ ਤੇ ਲਗਾਵਾਂਗੇ ਅਤੇ ਕੁੱਦਣ ਵਾਲੇ ਬੱਚਿਆਂ ਨੂੰ ਰੁਮਾਲ

ਨੂੰ ਛੂਹਣ ਨੂੰ ਕਹਾਂਗੇ । ਅਜਿਹਾ ਕਰਨ ਵਿਚ ਐਥਲੀਟ (Athletes) ਉੱਪਰ ਜਾਣਾ ਅਤੇ ਸਰੀਰ ਦੇ ਉੱਪਰਲੇ ਹਿੱਸੇ ਨੂੰ ਸਿੱਧਾ ਰੱਖਣਾ ਸਿੱਖ ਜਾਵੇਗਾ ।

ਅਖਾੜੇ ਵਿਚ ਡਿੱਗਣ ਦਾ ਢੰਗ ਲੈਂਡਿੰਗ
(METHOD OF LANDING)
ਦੋਹਾਂ ਪੈਰਾਂ ਨੂੰ ਇਕੱਠੇ ਕਰਕੇ ਐਥਲੀਟ ਪਿਟ (Pit) ਦੇ ਕੰਡੇ ਤੇ ਖੜੇ ਹੋ ਜਾਣਗੇ । ਭੁਜਾਵਾਂ ਨੂੰ ਅੱਗੇ ਪਿੱਛੇ ਵਲ ਲਿਆਉਣਗੇ ਅਤੇ Swing ਕਰਨਗੇ । ਨਾਲ ਹੀ ਗੋਡੇ ਵੀ ਝੁਕਾਉਣਗੇ ਅਤੇ ਹੱਥਾਂ ਬਾਹਵਾਂ ਨੂੰ ਇਕੱਠਿਆਂ ਪਿੱਛੇ ਵਲ ਲੈ ਜਾਣਗੇ । ਇਸ ਦੇ ਬਾਅਦ ਗੋਡੇ ਨੂੰ ਥੋੜ੍ਹਾ ਵਧਾ ਕੇ ਬਾਹਵਾਂ ਨੂੰ ਤੇਜ਼ੀ ਨਾਲ ਅੱਗੇ ਅਤੇ ਉੱਪਰ ਵਲ ਲੈ ਜਾਣਗੇ ਅਤੇ ਦੋਵਾਂ ਪੈਰਾਂ ਦੇ ਨਾਲ ਅਖਾੜੇ (Pit) ਵਿਚ ਜੰਪ ਕਰਨਗੇ । ਇਸ ਸਮੇਂ ਇਸ ਗੱਲ ਦਾ ਧਿਆਨ ਰਹੇ ਕਿ ਪੈਰ ਡਿਗਦੇ ਸਮੇਂ ਜਿੱਥੋਂ ਤਕ ਸੰਭਵ ਹੋਵੇ, ਸਿੱਧੇ ਰੱਖਣੇ ਚਾਹੀਦੇ ਹਨ ਅਤੇ ਇਸ ਦੇ ਨਾਲ ਹੀ ਪੱਠਿਆਂ ਨੂੰ ਅੱਗੇ ਧੱਕਣਾ ਚਾਹੀਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਕਿ ਸਰੀਰ ਵਿਚ ਪਿੱਛੇ ਝੁਕਾਅ (Arc) ਬਣ ਸਕੇ, ਜੋ ਕਿ ਹੈੱਗ ਸਟਾਈਲ (Hang Style) ਦੇ ਲਈ ਬਹੁਤ ਹੀ ਜ਼ਰੂਰੀ ਹੈ ।

ਐਥਲੀਟਸ (Athletes) ਨੂੰ ਸੱਤ ਕਦਮ ਕੁੱਦਣ ਲਈ ਆਖਾਂਗੇ । ਕੁੱਦਦੇ ਸਮੇਂ ਸੁਤੰਤਰ ਪੈਰ ਦੇ ਗੋਡੇ ਨੂੰ ਹਿਪ (Hip) ਦੇ ਬਰਾਬਰ ਲਿਆਵੇਗਾ । ਜਿਵੇਂ ਹੀ ਐਥਲੀਟ (Athlete) ਹਵਾ ਵਿਚ ਥੋੜ੍ਹੀ ਉੱਚਾਈ ਲਵੇਗਾ, ਸੁਤੰਤਰ ਪੈਰ ਨੂੰ ਪਿੱਛੇ ਵਲ ਅਤੇ ਹੇਠਾਂ ਵਲ ਲਿਆਵੇਗਾ ਜਿਸ ਨਾਲ ਉਹ ਕੁੱਦਣ ਵਾਲੇ ਪੈਰ
ਦੇ ਨਾਲ ਮਿਲ ਸਕੇ ਕੁੱਦਣ ਵਾਲਾ ਪੈਰ ਗੋਡਿਆਂ ਨਾਲ ਜੁੜਿਆ ਹੋਵੇਗਾ ਅਤੇ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਸਿੱਧਾ ਹੋਵੇ : ਜਦੋਂ ਖਿਡਾਰੀ ਹਵਾ ਵਿਚ ਉੱਚਾਈ ਲੈਂਦਾ ਹੈ, ਉਸ ਵੇਲੇ ਉਸ ਦੇ ਦੋਵੇਂ ਗੋਡਿਆਂ ਤੋਂ ਲੁਕੇ ਹੋਣਗੇ ਅਤੇ ਪੈਰ ਪੱਟ ਦੀ ਸੇਧ ਵਿਚ ਹੋਣਗੇ । ਦੋਵੇਂ ਭੁਜਾਵਾਂ ਸਿਰ ਦੇ ਬਗਲ ਵਿਚ ਅਤੇ ਉੱਪਰ ਵਲ ਹੋਣਵੀਆਂ ਸਰੀਰ ਪਿੱਛੇ ਵਲ ਝੁਕੀ ਹੋਈ ਦਸ਼ਾ ਵਿਚ ਅਤੇ ਜਿਵੇਂ ਹੀ ਐਥਲੀਟਸ (Athlets) ਅਖਾੜੇ (Pit) ਵਿਚ ਡਿੱਗਣ ਵਾਲੇ ਹੋਣ, ਉਹ ਸੁਤੰਤਰ ਪੈਰ ਗੋਡੇ ਤੋਂ ਝੁਕਾ ਕੇ ਅੱਗੇ ਨੂੰ ਅਤੇ ਉੱਪਰ ਨੂੰ ਲੈ ਜਾਣਗੇ, ਢਿੱਡ ਹੇਠਾਂ ਵਲ ਲਿਆਉਣਗੇ ਅਤੇ ਪੈਰਾਂ ਨੂੰ ਸਿੱਧਾ ਕਰਕੇ ਉੱਪਰ ਦੀ ਦਸ਼ਾ ਵਿਚ ਰੋਕਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਨਗੇ ।

ਹਿਚ ਕਿੱਕ ਦਾ ਢੰਗ
(METHOD OF HITCH KICK)

ਜੰਪ ਕਰਨ ਦੇ ਬਾਅਦ (Split) ਹਵਾ ਵਿਚ, ਪੈਰਾਂ ਨੂੰ ਅੱਗੇ ਪਿੱਛੇ ਕਰਕੇ, ਸੁਤੰਤਰ ਪੈਰ ਉੱਤੇ ਲੈਂਡਿੰਗ (Landing) ਕਰਨਾ ਪਰ ਉੱਪਰਲਾ ਹਿੱਸਾ ਅਤੇ ਸਿਰ ਸਿੱਧਾ ਰਹੇਗਾ, ਪਿੱਛੇ ਵਲ ਨਹੀਂ ਜਾਵੇ ।

ਇਸ ਤਰ੍ਹਾਂ ਹਵਾ ਵਿਚ ਸੁਤੰਤਰ ਪੈਰ ਨੂੰ ਰੱਖਣਗੇ ਅਤੇ ਕੁੱਦਣ ਵਾਲੇ ਪੈਰ ਨੂੰ ਅੱਗੇ . ਲੈ ਜਾ ਕੇ ਲੈਂਡਿੰਗ (Landing) ਕਰਨਗੇ ।

ਹੋਰ ਸਾਰੇ ਢੰਗ ਉਸੇ ਤਰ੍ਹਾਂ ਨਾਲ ਹੋਣਗੇ ਜਿਵੇਂ ਕਿ ਉੱਪਰ ਦੱਸਿਆ ਗਿਆ ਹੈ । ਸਿਰਫ ਸੁਤੰਤਰ ਪੈਰ ਨੂੰ ਲੈਡਿੰਗ (Lang) ਕਰਦੇ ਸਮੇਂ ਟੇਕ ਆਫ਼ ਪੈਰ ਦੇ ਨਾਲ ਲੈ ਆਉਣਗੇ ਅਤੇ ਦੋਹਾਂ ਪੈਰਾਂ ਤੇ ਇੱਕੋ ਵੇਲੇ ਜ਼ਮੀਨ ਤੇ ਆਉਣਗੇ । ਹੋਰ ਬਾਕੀ ਸਾਰੇ ਢੰਗ ਉਸੇ ਤਰ੍ਹਾਂ ਨਾਲ ਹੋਣਗੇ ਜਿਵੇਂ ਕਿ ਹੈਂਗ ਦੇ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ | ਐਥਲੀਟ (Athlet) ਨੂੰ ਭੱਜਣ ਦਾ ਰਸਤਾ (Approach Run) ਹੌਲੀ-ਹੌਲੀ ਵਧਾਉਂਦੇ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ |

ਉੱਪਰ ਦੀ ਕਿਰਿਆ ਨੂੰ ਕਈ ਵਾਰ ਕਰਨ ਦੇ ਬਾਅਦ ਇਸ ਕਿਰਿਆ ਨੂੰ ਸਪਰਿੰਗ ਬੋਰਡਾਂ (Sprin Board) ਦੀ ਮਦਦ ਨਾਲ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਜਿਵੇਂ ਕਿ ਜਿਮਨਾਸਟਿਕ (Gymnastic) ਵਾਲੇ ਕਰਦੇ ਹਨ । ਸਪਰਿੰਗ ਬੋਰਡ (Spring Board) ਦੀ ਘਾਟ ਵਿਚ ਇਸ ਕਿਰਿਆ ਨੂੰ ਕਿਸੇ ਹੋਰ ਉੱਚੀ ਥਾਂ ਤੇ ਵੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਕਿ ਐਥਲੀਟਸ ਨੂੰ ਹਵਾ ਵਿਚ ਸਹੀ ਕਿਰਿਆ ਢੰਗ ਕਰਨ ਦਾ ਅਭਿਆਸ ਹੋ ਜਾਵੇ |

ਟਰਿਪਲ ਜੰਪ (TRIPLE JUMP)

1. ਰਨਵੇ ਦੀ ਲੰਬਾਈ = 40 ਮੀ. ਤੋਂ 45 ਮੀ.
2. ਰਨਵੇ ਦੀ ਚੌੜਾਈ 3 .22 ਮੀ.
3. ਕਰਾਸ ਬਾਰ ਦੀ ਲੰਬਾਈ = 3.98 ਮੀ. ਤੋਂ 4.2 ਮੀ.
4. ਕਰਾਸ ਬਾਰ ਦਾ ਵਜ਼ਨ . – 2 ਕਿਲੋਗ੍ਰਾਮ
5. ਪਿਟ ਦੀ ਲੰਬਾਈ = 5 ਮੀ.’
6. ਪਿਟ ਦੀ ਚੌੜਾਈ = 275 ਮੀ. ਤੋਂ 3 ਮੀਟਰ
7. ਪਿਟ ਦੀ ਉੱਚਾਈ = 60 ਸੈਂ.ਮੀ.

ਅਪਰੋਚ ਰਨ (Approach Run)-ਲੰਮੀ ਛਾਲ ਦੀ ਤਰ੍ਹਾਂ ਇਸ ਵਿਚ ਵੀ ਅਪਰੋਚ ਰਨ ਲਿਆ ਜਾਵੇਗਾ ਪਰ ਸਪੀਡ (Speed) ਨਾ ਵਧੇਰੇ ਤੇਜ਼ ਅਤੇ ਨਾ ਵਧੇਰੇ ਹੌਲੀ ਹੋਵੇਗੀ ।


ਅਪਰੋਚ ਰਨ ਦੀ ਲੰਬਾਈ (Length of Approach Run)-ਟਰਿਪਲ ਜੰਪ ਵਿਚ 18 ਤੋਂ 22 ਕਦਮ ਜਾਂ 40 ਤੋਂ 45 ਮੀ: ਦੇ ਲਗਪਗ ਅਪਰੋਚ ਰਨ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਕੁੱਦਣ ਵਾਲੇ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਕਿ ਭੱਜਣ ਦੀ ਰਫ਼ਤਾਰ ਕਿਹੋ ਜਿਹੀ ਹੈ । ਹੌਲੀ ਰਫ਼ਤਾਰ ਵਾਲਾ ਲੰਮਾ ਅਪਰੋਚ ਲਵੇਗਾ, ਜਦੋਂ ਕਿ ਵਧੇਰੇ ਤੇਜ਼ ਰਫਤਾਰ ਵਾਲਾ ਛੋਟਾ ਅਪਰੋਚ ਲਵੇਗਾ । ਦੋਹਾਂ ਪੈਰਾਂ ਨੂੰ ਇਕੱਠਾ ਰੱਖ ਕੇ ਸ਼ੁਰੂ ਕਰਨਗੇ, ਭੱਜਣ ਦੀ ਰਫਤਾਰ ਨੂੰ ਆਮ ਰੱਖਣਗੇ । ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਸਿੱਧਾ ਰਹੇਗਾ ।

ਟੇਕ ਆਫ਼ (Take Off) ਲੈਂਦੇ ਸਮੇਂ ਗੋਡਾ ਲੰਮੀ ਛਾਲ ਦੀ ਬਜਾਇ ਇਸ ਵਿਚ ਘੱਟ ਝੁਕਿਆ ਹੋਵੇਗਾ । ਸਰੀਰ ਦਾ ਭਾਰ ਟੇਕ ਆਫ ਅਤੇ ਹੋਪ-ਸਟੈਂਪ (Hop Step) ਲੈਂਦੇ ਸਮੇਂ ਪਿੱਛੇ ਰਹੇਗਾ ਅਤੇ ਦੋਵੇਂ ਬਾਹਵਾਂ ਵੀ ਪਿੱਛੇ ਰਹਿਣਗੀਆਂ । ਦੂਸਰੀ ਲੱਤ ਤੇਜ਼ੀ ਨਾਲ ਵਿਚ ਆ ਕੇ ਸਪਲਿਟ ਪੁਜ਼ੀਸ਼ਨ (Split Position)ਬਣਾਵੇਗੀ ।

ਟਰਿਪਲ ਜੰਪ ਵਿਚ ਮੁੱਖ ਤੌਰ ਤੇ ਤਿੰਨ ਕਿਸਮ ਦੀ ਤਕਨੀਕ (Technique) ਪ੍ਰਚਲਿਤ ਹੈ –

1. ਫ਼ਲੈਟ ਤਕਨੀਕ
2. ਸਟੀਪ ਤਕਨੀਕ
3. ਮਿਕਸਡ ਤਕਨੀਕ |

ਤੀਹਰੀ ਛਾਲ (Triple Jumping)
ਉੱਚੀ ਛਾਲ (HIGH JUMP)

1. ਰਨਵੇ ਦੀ ਲੰਬਾਈ = 15 ਮੀ. ਤੋਂ 25 ਮੀ.
2. ਤਿਕੋਣੀ ਕਰਾਸਬਾਰ ਦੀ ਹਰੇਕ ਭੁਜਾ = 30 ਮਿ.ਮੀ.
3. ਕਰਾਸਬਾਰ ਦੀ ਲੰਬਾਈ = 3.98 ਮੀ. ਤੋਂ 4.02 ਮੀ.
4. ਕਰਾਸਬਾਰ ਦਾ ਵਜ਼ਨ = 2 ਕਿਲੋਗ੍ਰਾਮ
5. ਪਿਟ ਦੀ ਲੰਬਾਈ = 5 ਮੀ.
6. ਪਿਟ ਦੀ ਚੌੜਾਈ = 4 ਮੀ.
7. ਪਿਟ ਦੀ ਉੱਚਾਈ = 60 ਸੈਂ.ਮੀ.

1.ਸਾਰੇ ਟਰੈਕਾਂ ਨੂੰ ਪਹਿਲਾਂ ਦੋਹਾਂ ਪੈਰਾਂ ਤੇ ਇਕੋ ਵੇਲੇ ਆਪਣੀ ਥਾਂ ‘ਤੇ ਹੀ ਕੁੱਦਣ ਨੂੰ ਕਹਿਣਗੇ । ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਇਕ ਪੈਰ ਤੇ ਕੁੱਦਣ ਦਾ ਹੁਕਮ ਦੇਣਗੇ ।
ਉੱਪਰ ਉਛਲਦੇ ਸਮੇਂ ਇਹ ਧਿਆਨ ਰਹੇ ਕਿ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਸਿੱਧਾ ਰਹੇ ਅਤੇ ਹਰ ਵਾਰ ਹੀ ਕੁੱਦਿਆ ਜਾਵੇ । ਇਸ ਤਰ੍ਹਾਂ ਜਿਸ ਪੈਰ ਦੇ ਕੁੱਦਣ ਨਾਲ ਸੌਂਖ ਪ੍ਰਤੀਤ ਹੋਵੇ, ਉਸ ਨੂੰ ਉਛਾਲ ਉਠਾਣ) ਪੈਰ (Take off Foot) ਮੰਨ ਕੇ ਟਰੇਨਰਾਂ ਨੂੰ ਅੱਗੇ ਲਿਖੇ ਦੋ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ –

• ਖੱਬੇ ਪੈਰ ਤੇ ਕੁੱਦਣ ਵਾਲੇ ।
• ਸੱਜੇ ਪੈਰ ਤੇ ਕੁੱਦਣ ਵਾਲੇ ।

2. ਅੱਗੇ ਰੱਖ ਕੇ ਦੂਸਰੇ ਪੈਰ ਨੂੰ ਪਿੱਛੇ ਰੱਖਣਗੇ । ਦੋਹਾਂ ਬਾਹਾਂ ਨੂੰ ਇਕ ਵੇਲੇ ਪਿੱਛੇ ਤੋਂ ਅੱਗੇ, ਕੁਹਣੀਆਂ ਤੋਂ ਮੋੜ ਕੇ ਅੱਗੇ, ਉੱਪਰ ਵਲ ਤੇਜ਼ੀ ਨਾਲ ਜਾਣਗੇ ।
ਇਸ ਦੇ ਨਾਲ ਹੀ ਪਿੱਛੇ ਰੱਖੇ ਪੈਰ ਨੂੰ ਉੱਪਰ ਵਲ ਕਿੱਕ ਕਰਨਗੇ ਅਤੇ ਜ਼ਮੀਨ ਤੋਂ ਉਛਲ ਕੇ ਫਿਰ ਆਪਣੀ ਥਾਂ ਤੇ ਵਾਪਿਸ ਉਸੇ ਪੈਰ ਤੇ ਆਉਣਗੇ । ਇਸ ਸਮੇਂ ਉਛਾਲ ਪੈਰ (Take off Foot) ਵਾਲੇ ਪੈਰ ਦਾ ਗੋਡਾ ਵੀ ਉੱਪਰ ਉੱਠਦੇ ਸਮੇਂ ਥੋੜ੍ਹਾ ਮੁੜਿਆ ਹੋਵੇਗਾ, ਪਰ ਸਰੀਰ ਉੱਪਰਲਾ ਹਿੱਸਾ ਸਿੱਧਾ ਰਹੇਗਾ ਅਤੇ ਅੱਗੇ ਜਾ ਕੇ ਉੱਪਰ ਉੱਠੇਗਾ ਅਤੇ ਉਸ ਥਾਂ ਤੇ ਵਾਪਿਸ ਆਵੇਗਾ | ਉੱਪਰ ਜਾਂਦੇ ਸਮੇਂ ਲੱਕ ਅਤੇ ਅਗਲਾ ਪੈਰ ਸਿੱਧਾ ਰੱਖਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ਜਾਵੇ ।

3. ਸਿੱਖਣ ਵਾਲੇ 45° ਤੇ ਖੱਬੇ ਅਤੇ ਸੱਜੇ ਪੈਰ ਵਾਲੇ ਆਪਣੇ-ਆਪਣੇ ਪਾਸੇ ਖੜੇ ਹੋ ਕੇ ਛੜ ਨੂੰ ਦੋ ਫੁੱਟ ਦੀ ਉੱਚਾਈ ਤੇ ਰੱਖ ਕੇ ਅੱਗੇ ਤੁਰਦੇ ਹੋਏ ਉੱਪਰ ਦੀ ਤਰ੍ਹਾਂ ਉਛਾਲ ਕੇ ਕਰਾਸ ਬਾਰ ਨੂੰ ਪਾਰ ਕਰਨਗੇ ਅਤੇ ਉੱਪਰ ਜਾ ਕੇ ਹੇਠਾਂ ਆਉਂਦੇ ਸਮੇਂ ਉਸੇ ਟੇਕ ਆਫ ਫੁਟ ਤੇ ਵਾਪਿਸ ਆਉਣਗੇ । ਫਰਕ ਕੇਵਲ ਇੰਨਾ ਹੋਵੇਗਾ ਕਿ ਆਪਣੀ ਥਾਂ ਤੇ ਵਾਪਿਸ ਨਾ ਡਿਗ ਕੇ ਕਰਾਸ-ਬਾਰ ਨੂੰ ਪਾਰ ਕਰਨਗੇ । ਡਿਗਦੇ ਸਮੇਂ ਦੂਜਾ ਪੈਰ ਪਹਿਲੇ ਪੈਰ ਤੇ ਆਉਣ ਦੇ ਬਾਅਦ ਦਸ ਜਾਂ ਬਾਰਾਂ ਇੰਚ ਤੇ ਆਵੇਗਾ ਅਤੇ ਅੱਗੇ ਵਧੇਗਾ ।

4. ਕਰਾਸ ਬਾਰ ਦੀ ਉੱਚਾਈ ਵਧਾਉਂਦੇ ਹੋਏ ਮਿਲਣ ਵਾਲੇ ਨੂੰ ਟੇਕ ਆਫ ਫੁਟ ਨੂੰ ਲੰਮਾ ਕਰਨ ਲਈ ਕਹਾਂਗੇ । ਇਸ ਸਮੇਂ ਪੈਰ ਦੀ ਅੱਡੀ ਪਹਿਲਾਂ ਜ਼ਮੀਨ ਤੇ ਆਵੇ ।ਫਿਰ ਦੋਵੇਂ ਬਾਹਾਂ ਕੂਹਣੀਆਂ ਵਲ ਮੁੜੀਆਂ ਹੋਣ । ਕੁੱਦਦੇ ਸਮੇਂ ਧਿਆਨ ਕਰਾਸ ਬਾਰ ਤੇ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਸਿਰ ਸਰੀਰ ਦੇ ਕੁੱਝ ਪਿੱਛੇ ਲੁਕਿਆ ਹੋਵੇਗਾ ਅਤੇ ਪਿਛਲੇ ਪੈਰ ਉੱਪਰ ਕਰਦੇ ਸਮੇਂ ਪੈਰ ਦਾ ਪੰਜਾ ਉੱਪਰ ਵਲ ਸਿੱਧਾ ਹੋਵੇਗਾ ।

ਧਿਆਨ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ

ਇਸ ਵਿਚ ਹੇਠਲੀਆਂ ਗੱਲਾਂ ਨੂੰ ਧਿਆਨ ਵਿੱਚ ਰੱਖਿਆ ਜਾਵੇਗਾ –

1. ਦੋਹਾਂ ਬਾਹਾਂ ਨੂੰ ਤੇਜ਼ੀ ਨਾਲ ਉੱਪਰ ਲੈ ਜਾਣਗੇ ।
2. ਟੇਕ ਆਫ਼ ਫੁਟ (Take off foot) ਉਸ ਸਮੇਂ ਜ਼ਮੀਨ ਛੱਡੇਗਾ ਜਦੋਂ ਕਿ ਫਰੀ ਲੈਂਗ ਆਪਣੀ ਪੂਰੀ ਉਚਾਈ ਤਕ ਪੁੱਜ ਜਾਵੇਗੀ ।
3. ਉੱਪਰ ਦੱਸੀ ਗਈ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਜੋਗਿੰਗ (Jogging) ਦੇ ਨਾਲ ਵੀ ਕੀਤਾ ਜਾਵੇਗਾ ।
4. ਕਰਾਸ ਬਾਰ (Cross bar) ਨੂੰ ਦੋ ਫੁੱਟ (60 ਸੈਂ: ਮੀ:) ਉੱਚਾ ਰੱਖ ਕੇ ਖਿਡਾਰੀ ਨੂੰ: 3 ਦੀ ਤਰ੍ਹਾਂ ਕਰਾਸ ਛੇੜ (Cross bar) ਪਾਰ ਕਰਨ ਦੇ ਬਾਅਦ ਅਖਾੜੇ ਵਿਚ ਆਉਂਦੇ ਸਮੇਂ ਹਵਾ ਵਿਚ 90° ਤੇ ਘੁੰਮਣਗੇ ।
5. ਖੱਬੇ ਪੈਰ ਤੋਂ ਟੇਕ ਆਫ (Take off) ਲੈਣ ਵਾਲੇ ਖੱਬੇ ਪਾਸੇ ਘੁੰਮਣਗੇ ਅਤੇ ਸੱਜੇ ਪੈਰ ਤੇ ਟੇਕ ਆਫ (Take off) ਲੈਣ ਵਾਲੇ ਸੱਜੇ ਪਾਸੇ ਘੁੰਮਣਗੇ ।

ਇਸ ਵਿਚ ਦੋ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਿਆ ਜਾਵੇਗਾ –

1. ਖਿਡਾਰੀ ਉਛਾਲ (Take off) ਲੈਂਦੇ ਸਮੇਂ ਹੀ ਨਾ ਘੁੰਮਣ ਅਤੇ
2. ਪੂਰਨ ਉੱਚਾਈ ਪ੍ਰਾਪਤ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਨਾ ਘੁੰਮਣ ।

6. ਟੇਕ ਆਫ਼ ਫੁਟ (Take off Foot) ਨੂੰ ਅੱਗੇ ਰੱਖ ਕੇ ਖੜੇ ਹੋਣਗੇ ਪਰ ਇਹ ਧਿਆਨ ਰਹੇ ਕਿ ਸਰੀਰ ਦਾ ਭਾਰ ਅੱਡੀ ਤੇ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਫਰੀ ਲੈਂਗ (Free Leg) ਦੇ ਉੱਪਰ ਵਲ (Kick) ਕਿੱਕ ਕਰਨਗੇ, ਜਿਸ ਨਾਲ ਕੀ ਸਰੀਰ ਦਾ ਸਾਰਾ ਹਿੱਸਾ ਜ਼ਮੀਨ ਤੋਂ ਉੱਪਰ ਚੁੱਕਿਆ ਜਾਵੇ ।

7. ਜ਼ਮੀਨ ਤੋਂ ਚੂਨੇ ਦੀ ਸਮਾਨਾਂਤਰ ਰੇਖਾ ਲਿਜਾਵਾਂਗੇ । ਐਥਲੀਟ ਇਸ ਚੂਨੇ ਰੇਖਾ ਦੇ ਸੱਜੇ ਪਾਸੇ ਖੜ੍ਹੇ ਹੋ ਕੇ ਉੱਪਰ ਦਿੱਤੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਕਰਨਗੇ । ਉੱਪਰ ਹਵਾ ਵਿਚ ਪੁੱਜਦੇ ਹੀ ਖੱਬੇ ਪਾਸੇ ਟੇਕ ਆਫ਼ (Take off) ਨੂੰ ਘੁਮਾਉਣ, ਚਿਹਰਾ ਹੇਠਾਂ ਕਰਨਗੇ ਅਤੇ ਪਿਛਲੇ ਪੈਰ ਨੂੰ ਕਿੱਕ (Kick) ਦੇ ਨਾਲ ਉੱਪਰ ਚੁੱਕਣਗੇ । | ਇਸ ਵਿਚ ਮੁੱਖ ਤੌਰ ਤੇ ਇਹ ਧਿਆਨ ਰੱਖਿਆ ਜਾਵੇਗਾ ਕਿ ਫਰੀ ਲੈਂਗ (Free Leg) ਨੂੰ ਸਿੱਧੀ ਕਿੱਕ (Kick) ਕੀਤਾ ਜਾਵੇ । ਟੇਕ ਆਫ਼ ਲੈਂਗ (Take off Leg) ਨੂੰ ਸਿੱਧਾ ਕਿੱਕ ਗੋਡੇ ਮੋੜ ਕੇ (Bend) ਉੱਪਰ ਲੈ ਜਾਵਾਂਗੇ । ਖਿਡਾਰੀ ਕਸਬਾਰ (Cross bar) ਪਾਰ ਕਰਨ ਦੇ ਬਾਅਦ ਅਖਾੜੇ ਵਿਚ ਰੋਜ਼ ਅਭਿਆਸ ਕਰ ਸਕਦੇ ਹਨ, ਕਿਉਂਕਿ ਟੇਕ ਆਫ਼ ਕਿੱਕ ਤੇਜ਼ ਹੋਣ ਦੇ ਕਾਰਨ ਸੰਤੁਲਨ ਵੀ ਵਿਗੜ ਸਕਦਾ ਹੈ ।

8. ਤਿੰਨ ਕਦਮ ਤੋਂ ਆ ਕੇ ਜੰਪ ਕਰਨਾ (Jumping from three Steps)-ਕਰਾਸ ਬਾਰ ਦੇ ਸਮਾਨਾਂਤਰ ਇਕ ਡੇਢ ਫੁਟ ਤੋਂ 2 ਫੁਟ (45 ਸਮ ਤੋਂ 60 ਸਮ ਦੀ ਦੂਰੀ ਤੇ ਰੇਖਾ ਖਿੱਚਾਂਗੇ । ਇਸ ਰੇਖਾ ਤੋਂ 30° ਤੇ ਦੋਵੇਂ ਪੈਰ ਰੱਖ ਕੇ ਖੜੇ ਹੋਵਾਂਗੇ ਅਤੇ ਟੇਕ ਆਫ਼ ਫੁਟ (Take off foot) ਨੂੰ ਅੱਗੇ ਕੱਢਦੇ ਹੋਏ ਮੱਧਮ ਚਾਲ ਨਾਲ ਅੱਗੇ ਵੱਲ ਭੱਜਾਂਗੇ । ਜਿੱਥੇ ਤੀਸਰਾਂ ਪੈਰ ਆਵੇ ਉੱਥੇ ਨਿਸ਼ਾਨਾ ਲਾ ਦਿਓ ਅਤੇ ਹੁਣ ਉਸ ਥਾਂ ਤੇ ਦੋਵੇਂ ਰੱਖ ਕੇ ਕਸਬਾਰ (Cross bar) ਵਲ ਚੱਲਾਂਗੇ ਅਤੇ ਉੱਪਰ ਦੱਸੀ ਗਈ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਦੁਹਰਾਵਾਂਗੇ | ਕਸਬਾਰ ਦੀ ਉੱਚਾਈ ਐਥਲੀਟ ਦੀ ਸਹੂਲਤ ਅਨੁਸਾਰ ਵਧਾਉਂਦੇ ਜਾਵਾਂਗੇ ।

ਪੋਲ ਛਾਲ
(POLE VAULT)

• ਰਨਵੇ ਦੀ ਲੰਬਾਈ = 40 ਮੀ. ਤੋਂ 45 ਮੀ.
• ਰਨਵੇ ਦੀ ਚੌੜਾਈ = 1.22 ਮੀ.
• ਲੈਡਿੰਗ ਏਰੀਆ = 5 x 5 ਮੀ.
• ਤਿਕੋਣੀ ਕਰਾਸ ਬਾਰ ਦੀ ਲੰਬਾਈ । = 4.48 ਮੀ. ਤੋਂ 4.52 ਮੀ.
• ਤਿਕੋਣੀ ਕਰਾਸ ਬਾਰ ਦੀ ਹਰੇਕ ਭੁਜਾ = 30 ਸੈਂ.ਮੀ.
• ਕਰਾਸ ਬਾਰ ਦਾ ਵਜ਼ਨ = 2.25 ਕਿਲੋਗ੍ਰਾਮ
• ਲੈਂਡਿੰਗ ਏਰੀਏ ਦੀ ਉੱਚਾਈ । = 61 ਸੈਂ.ਮੀ. ਤੋਂ 91 ਸੈਂ.ਮੀ.
• ਵਾਲਟਿੰਗ ਬਾਕਸ ਦੀ ਲੰਬਾਈ = 1.08 ਮੀਟਰ
• ਬਾਕਸ ਦੀ ਚੌੜਾਈ ਰਨਵੇ ਵਾਲੇ ਪਾਸੇ = 60 ਸੈਂ.ਮੀ. ।

ਐਥਲੈਟਿਕਸ ਵਿਚ ਬਾਂਸ ਛਾਲ (Pole Vault) ਬਹੁਤ ਹੀ ਉਲਝਿਆ ਹੋਇਆ ਈਵੈਂਟ ਹੈ । ਕਿਸੇ ਈਵੈਂਟ ਵਿਚ ਟੇਕ ਆਫ਼ (Take off) ਦੇ ਅਖਾੜੇ ਵਿਚ ਆਉਂਦੇ ਸਮੇਂ ਤਕ ਇੰਨੀਆਂ ਕਿਰਿਆਵਾਂ ਦੀ ਲੋੜ ਨਹੀਂ ਹੁੰਦੀ, ਜਿੰਨੀ ਕਿ ਪੋਲ ਵਾਲਟ ਵਿਚ । ਇਸ ਲਈ ਇਸ ਈਵੈਂਟ ਨੂੰ ਪੜ੍ਹਾਉਣ ਅਤੇ ਸਿਖਾਉਣ ਦੋਹਾਂ ਵਿਚ ਹੀ ਪਰੇਸ਼ਾਨੀ ਹੁੰਦੀ ਹੈ । ਬਾਂਸ ਉਛਾਲ ਦੇ ਲਈ ਐਥਲੀਟ ਦੀ ਚੋਣ (Selection of Athletes for Pole Vault) – ਚੰਗਾ ਬਾਂਸ ਕੁੱਦਣ ਵਾਲਾ ਇਕ ਸਰਵਰ ਆਲ ਰਾਊਂਡਰ ਖਿਡਾਰੀ ਹੀ ਹੋ ਸਕਦਾ ਹੈ ਕਿਉਂਕਿ ਇਹ ਅਜਿਹੀ ਈਵੈਂਟ (Event) ਹੈ, ਜੋ ਕਿ ਸਭ ਤਰ੍ਹਾਂ ਨਾਲ ਸਰੀਰ ਦੀ ਯੋਗਤਾ ਨੂੰ ਬਣਾਏ ਰੱਖਦੀ ਹੈ, ਜਿਵੇਂ ਕਿ ਗਤੀ (Speed), ਸ਼ਕਤੀ (Strength), ਸਹਿਣਸ਼ੀਲਤਾ (Endurance) ਅਤੇ ਤਾਲਮੇਲ (Coordination) । ਬਾਂਸ ਕੁੱਦਣ ਵਾਲੇ ਨੂੰ ਇਕ ਚੰਗਾ ਜਿਮਨਾਸਟ ਵੀ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ, ਜਿਸ ਨਾਲ ਉਹ ਸਾਰੀਆਂ ਕਿਰਿਆਵਾਂ ਨੂੰ ਇੱਕੋ ਵੇਲੇ ਕਰ ਸਕੇ ।

ਪੋਲ ਦੀ ਪਕੜ ਅਤੇ ਲੈ ਕੇ ਤੁਰਨਾ (HOLDING AND CARRYING THE POLE) –
ਜ਼ਿਆਦਾਤਰ ਖੱਬੇ ਹੱਥ ਨਾਲ ਸਰੀਰ ਦੇ ਸਾਹਮਣੇ ਤਲੀ ਨੂੰ ਜ਼ਮੀਨ ਵੱਲ ਰੱਖਦੇ ਹੋਏ ਪੋਲ ਨੂੰ ਫੜਦੇ ਹਨ | ਸੱਜਾ ਹੱਥ ਸਰੀਰ ਦੇ ਪਿੱਛੇ ਪਿੱਠ (Hip) ਦੇ ਕੋਲ ਸੱਜੇ ਪਾਸੇ ਬਾਂਸ (Poll) ਦੇ ਆਖਰੀ ਸਿਰੇ ਵੱਲ ਹੁੰਦਾ ਹੈ । ਬਾਂਸ ਨੂੰ ਫੜਦੇ ਸਮੇਂ ਖੱਬਾ ਬਾਜੂ ਕੂਹਣੀ ਨਾਲ 100 ਅੰਸ਼ ਦਾ ਕੋਣ ਬਣਾਉਂਦਾ ਹੈ ਅਤੇ ਸਰੀਰ ਤੋਂ ਦੂਰ ਗੁੱਟ ਨੂੰ ਸਿੱਧਾ ਰੱਖਦੇ ਹੋਏ ਬਾਂਸ ਨੂੰ ਫੜਦੇ ਹਨ । ਸੱਜੇ ਹੱਥ ਨਾਲ ਜੋ ਕਿ ਬਾਂਸ ਦੇ ਆਖਰੀ ਸਿਰੇ ਵੱਲ ਹੁੰਦਾ ਹੈ, ਬਾਂਸ ਨੂੰ ਅੰਗੂਠੇ ਦੇ ਅੰਦਰੂਨੀ ਹਿੱਸੇ ਅਤੇ ਤਰਜਨੀ ਉਂਗਲੀ ਦੇ ਵਿਚਕਾਰ ਉੱਪਰੋਂ ਹੇਠਾਂ ਨੂੰ ਦਬਾਉਂਦੇ ਹੋਏ ਫੜਦੇ ਹਨ । ਦੋਵੇਂ ਕੂਹਣੀਆਂ 100 ਅੰਸ਼ ਦਾ ਕੋਣ ਬਣਾਉਂਦੀਆਂ ਹਨ । ਦੋਹਾਂ ਹੱਥਾਂ ਦੇ ਵਿਚਕਾਰ ਦੀ ਦੂਰੀ 24 ਇੰਚ (60 ਸੈਂ: ਮੀ:) ਤੋਂ 35 ਇੰਚ (80 ਸੈਂ: ਮੀ:) ਤਕ ਹੁੰਦੀ ਹੈ । ਇਹ ਬਾਂਸ ਕੁੱਦਣ ਵਾਲੇ ਦੇ ਸਰੀਰ ਦੀ ਬਨਾਵਟ ਤੇ ਅਤੇ ਪੋਲ ਨੂੰ ਲੈ ਕੇ ਭੱਜਦੇ ਸਮੇਂ ਜਿਸ ਦੀ ਹਾਲਤ ਵਿਚ ਉਸ ਨੂੰ ਆਰਾਮ ਮਹਿਸੂਸ ਹੋਣ, ਉਸ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ।

ਪੋਲ ਦੇ ਨਾਲ ਭੱਜਣ ਦੇ ਢੰਗ
(RUNNING WITH THE POLE)

1. ਬਾਂਸ ਨੂੰ ਸਿਰੇ ਤੋਂ ਉੱਪਰ ਰੱਖ ਕੇ ਤੁਰਨਾ (Walking with the pole keeping overhead-ਇਸ ਵਿਚ ਬਾਂਸ ਨੂੰ ਬਾਕਸ ਦੇ ਕੋਲ ਲਿਆਉਂਦੇ ਸਮੇਂ ਵੱਧ ਸਮਾਂ ਲੱਗਦਾ ਹੈ । ਇਸ ਲਈ ਇਹ ਢੰਗ ਵਧੇਰੇ ਢੁੱਕਵਾਂ ਨਹੀਂ ਹੈ ।
2. ਬਾਂਸ ਨੂੰ ਸਿਰ ਦੇ ਵਿਚਕਾਰ ਰੱਖ ਕੇ ਤੁਰਨਾ (Walking with pole keeping at the level of head)-ਸੰਸਾਰ ਦੇ ਜ਼ਿਆਦਾਤਰ ਬਾਂਸ ਕੁੱਦਣ ਵਾਲੇ ਇਸ ਢੰਗ ਨੂੰ ਅਪਣਾਉਂਦੇ ਹਨ । ਇਸ ਵਿਚ ਤੁਰਦੇ ਸਮੇਂ ਬਾਂਸ ਦਾ ਸਿਰਾ ਸਿਰ ਦੇ ਬਰਾਬਰ ਅਤੇ ਖੱਬੇ ਮੋਢੇ ਦੀ ਸੇਧ ਵਿਚ ਹੁੰਦਾ ਹੈ ।
   ਸੱਜੇ ਤੋਂ ਖੱਬੇ-ਇਸ ਵਿਚ ਮੋਢੇ ਅਤੇ ਬਾਹਾਂ ਸਾਧਾਰਨ ਹਾਲਤ ਵਿਚ ਰਹਿੰਦੇ ਹਨ ।
3. ਬਾਂਸ ਨੂੰ ਸਿਰ ਤੋਂ ਹੇਠਾਂ ਲੈ ਕੇ ਤੁਰਨਾ (Walking with pole keeping below the head-ਇਸ ਹਾਲਤ ਵਿਚ ਬਾਹਾਂ ਤੇ ਵਧੇਰੇ ਜ਼ੋਰ ਪੈਂਦਾ ਹੈ, ਜਿਸ ਦੇ ਕਾਰਨ ਬਾਕਸ ਤਕ ਆਉਂਦੇ-ਆਉਂਦੇ ਸਰੀਰ ਥੱਕ ਜਾਂਦਾ ਹੈ । ਬਹੁਤ ਹੀ ਘੱਟ ਸੰਖਿਆ ਵਿਚ ਲੋਕ ਇਸ ਨੂੰ ਕੰਮ ਵਿਚ ਲਿਆਉਂਦੇ ਹਨ ।

ਅਪਰੋਚ ਰਨ (Approach run)-ਐਥਲੀਟ ਨੂੰ ਆਪਣੇ ਉੱਪਰ ਯਕੀਨ ਉਦੋਂ ਹੁੰਦਾ ਹੈ, ਜਦੋਂ ਕਿ ਉਸਦਾ ਅਪਰੋਚ ਰਨ ਸਹੀ ਆਉਣਾ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ । ਅੱਗੇ ਦੀ ਕਿਰਿਆ ਤੇ ਇਸਦੇ ਬਾਅਦ ਹੀ ਵਿਚਾਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਇਸ ਦੇ ਲਈ ਸਭ ਤੋਂ ਚੰਗਾ ਢੰਗ (The best method) ਇਹ ਹੈ ਕਿ ਇਕ ਚੂਨੇ ਦੀ ਲਾਈਨ ਲਗਾ ਕੇ ਐਥਲੀਟ ਨੂੰ ਪੋਲ ਦੇ ਨਾਲ ਲਗਪਗ 150 ਫੁਟ (50 ਮੀ:) ਤਕ ਭੱਜਣ ਨੂੰ ਕਹਿਣਾ ।

ਇਸ ਕਿਰਿਆ ਨੂੰ ਕਈ ਦਿਨਾਂ ਤਕ ਕਰਨ ਨਾਲ ਐਥਲੀਟ ਦਾ ਪੈਰ ਇਕ ਥਾਂ ‘ਤੇ ਠੀਕ ਆਉਣ ਲੱਗੇਗਾ । ਉਸੇ ਵੇਲੇ ਤੁਸੀਂ ਦੂਰੀ ਨੂੰ ਫੀਤੇ ਨਾਲ ਨਾਪ ਲਓ, ਫਿਰ ਬਾਂਸ ਛਾਲ ਦੇ ਰਨ ਵੇਅ (Run way) ਤੇ ਕੰਮ ਕਰੋ । ਪੈਰਾਂ ਨੂੰ ਤੇਜ਼ੀ ਨਾਲ ਅਪਰੋਚ ਰਨ ਨੂੰ ਵੀ ਘਟਾਉਣਾ ਵਧਾਉਣਾ ਪੈਂਦਾ ਹੈ । ਬਾਂਸ ਛਾਲ ਦੇ ਅਪਰੋਚ ਰਨ (Approach run)-ਇਹ ਸਿਰਫ ਇਕ ਹੀ ਚਿੰਨ੍ਹ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਵਧੇਰੇ ਚਿੰਨ੍ਹ ਹੋਣ ਨਾਲ ਛਾਲ ਮਾਰਨ ਵਾਲਾ ਆਪਣੇ ਸਟਾਈਲ (Style) ਨੂੰ ਨਾ ਸੋਚ ਕੇ ਚੈੱਕ ਮਾਰਕ (Check Mark) ਨੂੰ ਸੋਚਦਾ ਰਹਿੰਦਾ ਹੈ । ਅਪਰੋਚ ਰਨ (Approach run) ਦੀ ਲੰਬਾਈ 40 ਤੋਂ 45 ਮੀ: ਦੇ ਲਗਪਗ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਅਖੀਰਲੀ 4 ਜਾਂ 6 ਕਦਮ ਤੋਂ ਵੱਧ ਤੇਜ਼ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਪੋਲ ਪਲਾਂਟ
(POLE PLANT)
ਇਹ ਸੰਭਵ ਨਹੀਂ ਕਿ ਤੁਸੀਂ ਪੂਰੀ ਤੇਜ਼ੀ ਨਾਲ ਪੋਲ (Pole) ਨੂੰ ਪਲਾਂਟ (Plant) ਕਰ ਸਕੋ, ਉਸ ਦੇ ਲਈ ਰਫ਼ਤਾਰ ਨੂੰ ਸੀਮਿਤ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਸਟੀਲ ਪੋਲ ( Ste Pyle ਵਿਚ ਪਲਾਂਟ ਜਲਦੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਫਾਇਬਰ ਗਲਾਸ (Fibre Glass) ਵਿਚ ਦੇਰੀ ਨਾਲ | ਸਟੀਲ ਪੋਲ ਵਿਚ ਪਲਾਂਟ ਕਰਦੇ ਸਮੇਂ ਔਥਲੀਟ ਨੂੰ “ਇਕ ਅਤੇ ਦੋ” ਗਿਣਨਾ ਚਾਹੀਦਾ ਹੈ । ਇਕ ਕਹਿਣ ‘ਤੇ ਖੱਬਾ ਪੈਰ ਅੱਗੇ ਟੇਕ ਆਫ (Take off) ਦੇ ਲਈ ਆਵੇ ਅਤੇ ਸੱਜੇ ਪੈਰ ਦਾ ਗੋਡਾ ਉੱਪਰ ਵਲ ਜਾਵੇਗਾ । ਦੋ ਕਹਿਣ ਤੇ ਸਰੀਰ ਦੀ ਸਵਿੰਗ (Swing) ਸ਼ੁਰੂ ਹੋ ਜਾਣੀ ਹੈ | ਇਸ ਸਮੇਂ ਵਾਲਟਰ (Vaulter) ਨੂੰ ਆਪਣੀ ਖੱਬੀ ਲੱਤ ਨੂੰ ਆਜ਼ਾਦ ਛੱਡ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਕਿ ਉਹ ਸੱਜੀ ਲੱਤ ਦੇ ਨਾਲ ਮਿਲ ਸਕੇ । ਇਸ ਢੰਗ ਨਾਲ ਚੰਗੀ ਸਵਿੰਗ ਲੈਣ ਵਿਚ ਸਹੂਲਤ ਹੁੰਦੀ ਹੈ ।

ਟੇਕ ਆਫ (TAKE OFF)
ਟੇਕ ਆਫ ਦੇ ਸਮੇਂ ਸੱਜਾ ਗੋਡਾ ਅੱਗੇ ਆਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਨਾਲ ਸਰੀਰ ਨੂੰ ਉੱਪਰ ਪੋਲ ਵੱਲ ਲੈ ਜਾਂਦੇ ਹਨ ਅਤੇ ਸੀਨੇ ਨੂੰ ਪੋਲ ਵਲ ਖਿੱਚਦੇ ਹਨ । ਪੋਲ ਨੂੰ ਸੀਨੇ ਦੇ ਸਾਹਮਣੇ ਰੱਖਦੇ ਹਨ । ਸਵਿੰਗ (Swing) ਦੇ ਸਮੇਂ ਸੱਜੀ ਲੱਤ ਸਰੀਰ ਦੇ ਅੱਗੇ ਉੱਪਰ ਵੱਲ ਉੱਠੇਗੀ । ਨੋਟ-ਪੋਲ ਕਰਦੇ ਸਮੇਂ ਐਥਲੀਟ ਆਪਣੀ ਹਿੱਪ ਨੂੰ ਪਹਿਲਾਂ ਉੱਚਾ ਲੈ ਆਉਂਦੇ ਹਨ, ਜਦੋਂ ਕਿ ਲੱਤਾਂ ਨੂੰ ਉੱਪਰ ਆਉਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਹਿੱਪ ਨੂੰ ਹੇਠਾਂ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਪੋਲ ਵਾਲਟਰਾਂ ਨੂੰ ਇਹ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਜਦੋਂ ਤਕ ਪੋਲ ਸਿੱਧਾ ਨਹੀਂ ਹੁੰਦਾ, ਉਨ੍ਹਾਂ ਨੂੰ ਪੋਲ ਦੇ ਨਾਲ ਹੀ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ । ਪੋਲ ਛੱਡਦੇ ਸਮੇਂ ਹੇਠਲਾਂ ਹੱਥ ਪਹਿਲਾਂ ਛੱਡਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਹ ਦੇਖਿਆ ਗਿਆ ਹੈ ਕਿ ਬਹੁਤ ਸਾਰੇ ਨਵੇਂ ਪੋਲ ਵਾਲਟਰ ਆਪਣੀ ਪਿੱਠ ਨੂੰ ਕਰਾਸ ਬਾਰ ਦੇ ਉੱਪਰੋਂ ਲੈ ਜਾਂਦੇ ਹਨ । ਇਹ ਸਿਰਫ ਉੱਪਰਲੇ ਹੱਥ ਨੂੰ ਪਹਿਲਾਂ ਛੱਡਣ ਨਾਲ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਯੋ-ਈਵੈਂਟਸ ਕਿਹੜੇ-ਕਿਹੜੇ ਹੁੰਦੇ ਹਨ ? ਉਨ੍ਹਾਂ ਦੀ ਤਕਨੀਕ ਅਤੇ ਨਿਯਮਾਂ ਬਾਰੇ ਲਿਖੋ :
ਉੱਤਰ :
ਸ਼ਾਟ ਪੁਟ-ਪੈਰੀ ਉਵਰਾਇਨ ਢੰਗ
(SHOT PUT-PERI OVERAIN METHOD)

1. ਮੁੱਢਲੀ ਸਥਿਤੀ (Initial Position)-ਥੋਅਰ ਗੋਲਾ ਸੁੱਟਣ ਦੀ ਹਾਲਤ ਵਿਚ ਆਪਣੀ ਪਿੱਠ ਕਰਕੇ ਖੜ੍ਹਾ ਹੋਵੇਗਾ |

ਸਰੀਰ ਦਾ ਭਾਰ ਸੱਜੇ ਪੈਰ ਤੇ ਹੋਵੇਗਾ, ਸਰੀਰ ਦੇ ਉੱਪਰਲੇ ਹਿੱਸੇ ਨੂੰ ਹੇਠਾਂ ਲਿਆਉਂਦੇ ਸਮੇਂ ਪੈਰ ਦੀ ਅੱਡੀ ਉੱਪਰ ਉੱਠੇਗੀ ਅਤੇ ਖੱਬਾ ਪੈਰ ਗੋਡੇ ਤੋਂ ਮੁੜੀ ਹਾਲਤ ਵਿਚ ਪਿੱਛੇ ਉੱਪਰ ਜਾ ਕੇ ਫੌਰਨ ਸੱਜੇ ਪੈਰ ਦੇ ਕੋਲ ਫਿਰ ਲਿਆਵਾਂਗੇ । ਦੋਵੇਂ ਪੈਰ ਮੋੜੇ ਹੋਣਗੇ ਅਤੇ ਉੱਪਰਲਾ ਹਿੱਸਾ ਅੱਗੇ ਵੱਲ ਝੁਕਿਆ ਹੋਵੇਗਾ ।

2. ਗਲਾਈਡ (Glide)-ਸੱਜਾ ਪੈਰ ਸਿੱਧਾ ਕਰਾਂਗੇ ਅਤੇ ਸੱਜੇ ਪੈਰ ਦੇ ਪੰਜੇ ਅਤੇ ਅੱਡੀ ਦੇ ਪਿੱਛੇ ਆਉਣਗੇ । ਖੱਬਾ ਪੈਰ ਸਟਾਪ ਬੋਰਡ (Stop Board) ਵਲ ਤੇਜ਼ੀ ਨਾਲ ਕਿੱਕ ਕਰਾਂਗੇ । ਬੈਠੀ ਹੋਈ ਹਾਲਤ ਵਿਚ ਪੱਠਿਆਂ ਨੂੰ ਪਿੱਛੇ ਅਤੇ ਹੇਠਾਂ ਵਲ ਸੁੱਟਾਂਗੇ । ਸੱਜਾ ਪੈਰ ਜ਼ਮੀਨ ਤੋਂ ਉੱਪਰ ਉੱਠੇਗਾ ਅਤੇ ਸਰੀਰ ਦੇ ਹੇਠਾਂ ਲਿਆ ਕੇ ਖੱਬੇ ਪਾਸੇ ਨੂੰ ਪੰਜਾ ਮੋੜ ਕੇ ਰੱਖਾਂਗੇ । ਖੱਬਾ ਪੈਰ ਇਸ ਦੇ ਲਗਪਗ ਨਾਲ ਹੀ ਸਟਾਪ ਬੋਰਡ (Stop Board) ਤੋਂ ਥੋੜਾ ਸੱਜੇ ਪਾਸੇ ਜ਼ਮੀਨ ‘ਤੇ ਲੱਗੇਗਾ । ਦੋਵੇਂ ਪੈਰਾਂ ਦੇ ਪੰਜਿਆਂ ਨੂੰ ਜ਼ਮੀਨ ’ਤੇ ਲਿਆਵਾਂਗੇ । ਦੋਵੇਂ ਮੋਢੇ ਪਿੱਛੇ ਵਲ ਝੁਕੇ ਹੋਣਗੇ । ਸਰੀਰ ਦਾ ਸਾਰਾ ਭਾਰ ਸੱਜੇ ਪੈਰ ਤੇ ਹੋਵੇਗਾ ।

3. ਆਖਰੀ ਚਰਨ (Final Phase)-ਸੱਜੇ ਪੈਰ ਦੇ ਪੰਜੇ ਅਤੇ ਗੋਡੇ ਨੂੰ ਇਕ ਵੇਲੇ ਖੱਬੇ ਪਾਸੇ ਵੱਲ ਘੁਮਾਵਾਂਗੇ ਅਤੇ ਦੋਵੇਂ ਪੈਰਾਂ ਨੂੰ ਸਿੱਧਾ ਕਰਾਂਗੇ । ਪੱਠਿਆਂ ਨੂੰ ਵੀ ਅੱਗੇ ਵਧਾਵਾਂਗੇ । ਸਰੀਰ ਦਾ ਭਾਰ ਦੋਵੇਂ ਪੈਰਾਂ ਤੇ ਹੋਵੇਗਾ । ਖੱਬਾ ਮੋਢਾ ਸਾਹਮਣੇ ਵੱਲ ਖੁੱਲ੍ਹੇਗਾ | ਸੱਜਾ ਮੋਢਾ ਖੱਬੇ ਪਾਸੇ ਵੱਲ ਉੱਪਰ ਉੱਠੇਗਾ ਅਤੇ ਘੁੰਮੇਗਾ । ਢਿੱਡ ਦੀ ਸਥਿਤੀ ਧਨੁਸ਼ ਦੇ ਆਕਾਰ ਵਿਚ ਪਿਛੇ ਵੱਲ ਝੁਕੀ ਹੋਈ ਹੋਵੇਗੀ ।

4. ਗੋਲਾ ਸੁੱਟਣਾ/ਥਰੋ ਕਰਨਾ (Putting/Throwing the shot)-ਸੱਜਾ ਮੋਢਾ ਅਤੇ ਸੱਜੀ ਬਾਂਹ ਗੋਲੇ ਦੇ ਅੱਗੇ ਵੱਲ ਜਾਣਗੇ | ਸੱਜਾ ਮੋਢਾ ਅੱਗੇ ਵਲ ਵਧਦਾ ਰਹੇਗਾ | ਸਰੀਰ ਦਾ ਸਾਰਾ ਭਾਰ ਖੱਬੇ ਪੈਰ ਤੇ ਹੋਵੇਗਾ | ਖੱਬਾ ਮੋਢਾ ਅੱਗੇ ਵਲ ਵਧਦਾ ਰਹੇਗਾ | ਸਰੀਰ ਦਾ ਸਾਰਾ ਭਾਰ ਸੱਜੇ ਪੈਰ ‘ਤੇ ਹੋਵੇਗਾ ਜੋ ਕਿ ਪੂਰੀ ਤਰ੍ਹਾਂ ਸਿੱਧਾ ਹੋਵੇਗਾ ਜਿਵੇਂ ਕਿ ਸੱਜੇ ਹੱਥ ਰਾਹੀਂ ਗੋਲੇ ਨੂੰ ਅੱਗੇ ਸੁੱਟਿਆ ਜਾਵੇਗਾ । ਦੋਹਾਂ ਪੈਰਾਂ ਦੀ ਸਥਿਤੀ ਬਦਲ ਜਾਵੇਗੀ । ਖੱਬਾ ਪੈਰ ਪਿੱਛੇ ਆਵੇਗਾ ਅਤੇ ਸੱਜਾ ਪੈਰ ਅੱਗੇ ਆਵੇਗਾ | ਸਰੀਰ ਦਾ ਭਾਰ ਸੱਜੇ ਪੈਰ ‘ਤੇ ਹੋਵੇਗਾ ਉੱਪਰਲਾ ਭਾਗ ਅਤੇ ਸੱਜਾ ਪੈਰ ਦੋਵੇਂ ਅੱਗੇ ਨੂੰ ਝੁਕੇ ਹੋਣਗੇ ।

ਘੁੰਮ ਕੇ ਗੋਲਾ ਸੁੱਟਣਾ ਜਾਂ ਚੱਕੇ ਦੀ ਤਰ੍ਹਾਂ ਸੁੱਟਣਾ (THROWING THE SHOT BY ROTATING OR LIKE A DISCUS)

1. ਮੁੱਢਲੀ ਸਥਿਤੀ (Initial Position) -ਸ਼ੁਰੂ ਕਰਨ ਲਈ ਗੋਲੇ ਦੇ ਦੂਜੇ ਹਿੱਸੇ ਤੇ ਗੋਲਾ ਸੁੱਟਣ ਦੀ ਹਾਲਤ ਵਿਚ ਪਿੱਠ ਕਰਕੇ ਖੜੇ ਹੋਵਾਂਗੇ । ਖੱਬਾ ਪੈਰ ਮੱਧ ਰੇਖਾ ਤੇ ਅਤੇ ਸੱਜਾ ਹਿੱਸਾ ਸੱਜੇ ਪਾਸੇ ਹੋਵੇਗਾ | ਸੱਜਾ ਪੈਰ ਲੋਹੇ ਦੇ ਰਿਮ (Rim) ਤੋਂ 5 ਤੋਂ 8 ਸੈਂ: ਮੀ: ਪਿੱਛੇ ਰੱਖਾਂਗੇ, ਤਾਂ ਜੋ ਘੁੰਮਦੇ ਸਮੇਂ ਫਾਉਲ (Foul) ਨਾ ਹੋਵੇ । ਗੋਲਾ ਗਰਦਨ ਦੇ ਹੇਠਲੇ ਹਿੱਸੇ ਵਿਚ ਹੋਵੇਗਾ, ਕੁਹਣੀ ਉੱਪਰ ਉੱਠੀ ਹੋਵੇਗੀ । ਸ਼ੁਰੂ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਮੋਢਾ, ਢਿੱਡ, ਖੱਬੀ ਬਾਂਹ, ਗੋਲਾ-ਸਾਰੇ ਪਹਿਲਾਂ ਖੱਬੇ ਪਾਸੇ ਨੂੰ ਘੁੰਮਣਗੇ ਅਤੇ ਬਾਅਦ ਵਿਚ ਸੱਜੇ ਪਾਸੇ ਜਾਣਗੇ | ਅਜਿਹਾ ਕਰਦੇ ਸਮੇਂ ਦੋਵੇਂ ਗੋਡੇ ਝੁਕੇ ਹੋਣਗੇ ।

2. ਘੁੰਮਣਾ (Rotation)-ਦੋਹਾਂ ਪੈਰਾਂ ਉੱਤੇ ਸਰੀਰ ਦਾ ਭਾਰ ਹੋਵੇਗਾ ਅਤੇ ਉੱਪਰ ਦੀ ਸਥਿਤੀ ਵਿਚ ਸਿਰਫ ਇਕ ਸਵਿੰਗ (Swing) ਲੈਣ ਦੇ ਬਾਅਦ ਘੁੰਮਣਾ ਸ਼ੁਰੂ ਹੋ ਜਾਵੇਗਾ । ਮੋਢਾ ਅਤੇ ਧੜ ਸੱਜੇ ਪਾਸੇ ਵਲ ਪੂਰੀ ਤਰ੍ਹਾਂ ਘੁੰਮਦੇ ਸਮੇਂ ਸਰੀਰ ਦਾ ਭਾਰ ਵੀ ਖੱਬੇ ਪੈਰ ’ਤੇ ਚਲਾ ਜਾਵੇਗਾ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਖੱਬੇ ਪਾਸੇ ਖੱਬੀ ਬਾਂਹ ਨੂੰ ਜ਼ਮੀਨ ਤੇ ਸਮਾਨਾਂਤਰ ਰੱਖਦੇ ਹੋਏ ਖੱਬੇ ਪੈਰ ਦੇ ਪੰਜੇ ਤੇ ਸਰੀਰ ਦਾ ਭਾਰ ਲਿਆਉਂਦੇ ਹੋਏ ਦੋਵੇਂ ਗੋਡੇ ਝੁਕਾ ਕੇ ਘੁਮਾਵਾਂਗੇ । ਸੱਜੇ ਪੈਰ ਦੇ ਪੰਜੇ ਤੇ ਵੀ 90 ਅੰਸ਼ ਤਕ ਘੰਮਾਣਗੇ । ਸੱਜੇ ਪੈਰ ਨੂੰ ਮੋਢੇ ਤੋਂ ਝੁਕੀ ਹੋਈ ਹਾਲਤ ਵਿਚ ਖੱਬੇ ਪੈਰ ਦੇ ਗਿੱਟੇ ਦੇ ਉੱਪਰੋਂ ਗੋਲੇ ਦੇ ਵਿਚਕਾਰ ਪਹੁੰਚਣ ਤੇ ਲਿਆਵਾਂਗੇ । ਖੱਬੇ ਪੈਰ ਤੇ ਘੁੰਮਦੇ ਸਮੇਂ ਚੱਕਰ ਖ਼ਤਮ ਹੋਣ ਤੇ ਹਵਾ ਵਿਚ ਦੋਵੇਂ ਪੈਰ ਹੋਣਗੇ ਅਤੇ ਲੱਕ ਨੂੰ ਘੁਮਾਵਾਂਗੇ ।

ਸੱਜਾ ਪੈਰ ਕੇਂਦਰ ਵਿਚ ਸੱਜੇ ਪੈਰ ਦੇ ਪੰਜੇ `ਤੇ ਆਵੇਗਾ । ਸੱਜੇ ਪੈਰ ਦੇ ਪੰਜੇ ਦੀ ਸਥਿਤੀ ਉਸੇ ਤਰ੍ਹਾਂ ਨਾਲ ਹੋਵੇਗੀ ਜਿਵੇਂ ਕਿ ਘੜੀ ਵਿਚ 2 ਵਜੇ ਦੀ ਹਾਲਤ ਵਿਚ ਸੂਈ ਹੁੰਦੀ ਹੈ । ਬਹਾਦਰ ਸਿੰਘ ਦਾ ਪੈਰ 10 ਵਜੇ ਦੀ ਸਥਿਤੀ ਵਿਚ ਆਉਂਦਾ ਹੈ । ਹਵਾ ਵਿਚ ਹੀ ਲੱਕ ਨੂੰ ਮੋੜ ਲੈਂਦਾ ਹੈ । ਦੁਸਰੀ ਸਥਿਤੀ ਵਿਚ ਖੱਬਾ ਪੈਰ ਟੋਅ ਬੋਰਡ (Toe-Board) ਤੋਂ ਕੁੱਝ ਦੇਰੀ ਨਾਲ ਆਵੇਗਾ ਪਰ ਉੱਪਰਲੇ ਹਿੱਸੇ ਨੂੰ ਕੇਂਦਰ ਵਿਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । 10 ਵਜੇ ਦੀ ਸਥਿਤੀ ਵਿਚ ਖੱਬਾ ਪੈਰ ਜ਼ਮੀਨ ‘ਤੇ ਤੇਜ਼ੀ ਨਾਲ ਆਵੇਗਾ ਅਤੇ ਜ਼ਿਆਦਾਤਰ ਇਹ ਸੰਭਾਵਨਾ ਰਹਿੰਦੀ ਹੈ ਕਿ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਜਲਦੀ ਉੱਪਰ ਆ ਜਾਂਦਾ ਹੈ ।

ਹੇਠ ਲਿਖੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਾਂਗੇ –

1. ਸ਼ੁਰੂ ਵਿਚ ਸੰਤੁਲਨ ਠੀਕ ਬਣਾ ਕੇ ਚੱਲਾਂਗੇ, ਖੱਬਾ ਪੈਰ ਹੇਠਾਂ ਰੱਖਾਂਗੇ ।
2. ਸੱਜੇ ਪੈਰ ਤੋਂ ਪੂਰੀ ਗਲਾਈਡ (Glide) ਲਵਾਂਗੇ, ਜੰਪ (Jump) ਨਹੀਂ ਕਰਾਂਗੇ । ਸਰੀਰ ਦੇ ਉੱਪਰਲੇ ਹਿੱਸੇ ਨੂੰ ਉੱਪਰ ਨਹੀਂ ਚੁੱਕਾਂਗੇ ।
3. ਸੱਜਾ ਪੈਰ ਕੇਂਦਰ ਵਿਚ ਆਉਂਦੇ ਸਮੇਂ ਅੰਦਰ ਨੂੰ ਘੁੰਮਿਆ ਹੋਵੇਗਾ ।
4. ਖੱਬੇ ਮੋਢੇ ਅਤੇ ਪੱਠੇ ਨੂੰ ਜਲਦੀ ਉੱਪਰ ਨਹੀਂ ਲਿਆਂਦਾ ਜਾਵੇਗਾ ।
5. ਖੱਬੀ ਬਾਂਹ ਨੂੰ ਸਰੀਰ ਦੇ ਕੋਲ ਰੱਖਾਂਗੇ ।
6. ਖੱਬਾ ਪੈਰ ਜ਼ਮੀਨ ਤੇ ਨਾ ਜਲਦੀ ਲੱਗੇ ਅਤੇ ਨਾ ਜ਼ਿਆਦਾ ਦੇਰ ਨਾਲ ।

ਸਾਧਾਰਨ ਨਿਯਮ (GENERAL RULES)
1. ਗੋਲੇ ਦਾ ਭਾਰ ਮਰਦ ਵਰਗ ਵਿਚ 7.26 ਕਿਲੋ ਗਾਮ, ਔਰਤ ਵਰਗ ਵਿਚ 4.00 ਕਿਲੋ ਗਾਮ । ਗੋਲੇ ਦਾ ਵਿਆਸ ਮਰਦ ਵਰਗ ਵਿਚ 110 ਤੋਂ 130 ਸੈਂਟੀਮੀਟਰ ਅਤੇ ਔਰਤਾਂ ਵਿਚ 95 ਤੋਂ 110 ਸੈਂਟੀਮੀਟਰ ।

2. ਗੋਲੇ ਅਤੇ ਤਾਰ ਗੋਲੇ ਨੂੰ 2.135 ਮੀਟਰ ਦੇ ਚੱਕਰ ਤੋਂ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਅੰਦਰਲਾ ਹਿੱਸਾ ਪੱਕਾ ਹੋਵੇਗਾ, ਬਾਹਰਲੇ ਮੈਦਾਨ ਤੋਂ 25 ਸੈਂਟੀਮੀਟਰ ਹੇਠਾਂ ਹੋਵੇਗਾ | ਸਟਾਪ ਬੋਰਡ (Stop Board) 1.22 ਮਿਲੀ ਮੀਟਰ ਲੰਬਾ, 114 ਮਿਲੀਮੀਟਰ ਚੌੜਾ ਅਤੇ 106 ਮਿਲੀਮੀਟਰ ਉੱਚਾ ਹੋਵੇਗਾ ।

3. ਸੈਕਟਰ 40 ਅੰਸ਼ ਦਾ ਗੋਲਾ, ਤਾਰ ਗੋਲਾ ਅਤੇ ਚੱਕਾ ਹੋਵੇਗਾ | ਕੇਂਦਰ ਤੋਂ ਇਕ ਰੇਖਾ ਸਿੱਧੀ 20 ਮੀਟਰ ਦੀ ਖਿੱਚਾਂਗੇ । ਇਸ ਰੇਖਾ ਨੂੰ 18.84 ਤੇ ਇਕ ਬਿੰਦੁ ਲਾਵਾਂਗੇ । ਇਸ ਬਿੰਦੂ ਤੋਂ ਦੋਵੇਂ ਪਾਸੇ 6.84 ਦੀ ਦੂਰੀ ਤੇ ਦੋ ਬਿੰਦੂ ਪਾ ਦਿਆਂਗੇ ਅਤੇ ਇਨ੍ਹਾਂ ਹੀ ਦੋ ਬਿੰਦੂਆਂ ਤੋਂ ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ਖਿੱਚਣ ’ਤੇ 40 ਅੰਸ਼ ਦਾ ਕੋਣ ਬਣੇਗਾ । ਗੋਲਾ ਸੁੱਟਦੇ ਸਮੇਂ ਸਰੀਰ ਦਾ ਸੰਤੁਲਨ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਗੋਲਾ ਸੁੱਟ ਕੇ ਗੋਲਾ ਜ਼ਮੀਨ ਤੇ ਡਿਗਣ ਦੇ ਬਾਅਦ 75 ਸੈਂਟੀਮੀਟਰ ਦੀਆਂ ਦੋਵੇਂ ਰੇਖਾਵਾਂ ਜੋ ਕਿ ਗੋਲਾ ਸੁੱਟਣ ਦੇ ਖੇਤਰ ਨੂੰ ਦੋ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡਦੀਆਂ ਹਨ, ਉਸ ਦੇ ਪਿੱਛਲੇ ਹਿੱਸੇ ਤੋਂ ਬਾਹਰ ਆਉਣਗੇ । ਗੋਲਾ ਇਕ ਹੱਥ ਨਾਲ ਪੁੱਟ ਕੀਤਾ ਜਾਵੇਗਾ, ਸੁੱਟਿਆ ਨਹੀਂ ਜਾਵੇਗਾ । ਗੋਲਾ ਮੋਢੇ ਦੇ ਪਿੱਛੇ ਨਹੀਂ ਆਵੇਗਾ, ਸਿਰਫ ਧੌਣ ਕੋਲ ਰਹੇਗਾ | ਸਹੀ ਪੁਟ ਉਸ ਨੂੰ ਮੰਨਾਂਗੇ ਜੋ ਸੈਕਟਰ ਦੇ ਅੰਦਰ ਹੋਵੇ । ਸੈਕਟਰ ਦੀਆਂ ਰੇਖਾਵਾਂ ਨੂੰ ਕੱਟਣ ‘ਤੇ ਫਾਉਲ (Foul) ਮੰਨਿਆ ਜਾਵੇਗਾ । ਜੇ ਅੱਠ ਪ੍ਰਤੀਯੋਗੀ (Competitors) ਹਨ ਤਦ ਸਾਰਿਆਂ ਨੂੰ 6 ਮੌਕੇ ਦੇਵਾਂਗੇ ਨਹੀਂ ਤਾਂ ਟਾਈ ਪੈਣ ਤੇ 9 ਵੀ ਹੋ ਸਕਦੇ ਹਨ ।

ਚੱਕਾ ਸੁੱਟਣ ਦਾ ਆਰੰਭ
(INITIAL STANCE OF DISCUS THROW)
ਚੱਕਾ ਸੁੱਟਣ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ ਪਿੱਠ ਕਰਕੇ ਛੱਲੇ (Ring) ਦੇ ਕੋਲ ਚੱਕਰ ਵਿਚ ਖੜ੍ਹੇ ਹੋਵਾਂਗੇ । ਸੱਜੀ ਬਾਂਹ ਨੂੰ ਘੁਮਾਉਂਦੇ ਹੋਏ ਇਕ ਜਾਂ ਦੋ ਸਵਿੰਗ (Swing) ਬਾਂਹ ਅਤੇ ਹੜ ਨੂੰ ਨਾਲ ਹੀ ਘੁਮਾਉਂਦੇ ਹੋਏ ਲਵਾਂਗੇ । ਅਜਿਹਾ ਕਰਦੇ ਸਮੇਂ ਸਰੀਰ ਦਾ ਭਾਰ ਵੀ ਇਕ ਪੈਰ ਤੋਂ ਦੂਸਰੇ ਪੈਰ ਤੇ ਜਾਵੇਗਾ ਜਿਸ ਨਾਲ ਪੈਰਾਂ ਦੀਆਂ ਅੱਡੀਆਂ ਮੈਦਾਨ ਦੇ ਉੱਪਰ ਉੱਠਣਗੀਆਂ । ਜਦੋਂ ਚੱਕਾ ਸੱਜੇ ਪਾਸੇ ਹੋਵੇਗਾ ਅਤੇ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਵੀ ਸੱਜੇ ਪਾਸੇ ਮੁੜਿਆ ਹੋਵੇਗਾ, ਇੱਥੋਂ ਚੱਕਰ ਦਾ ਆਰੰਭ ਹੋਵੇਗਾ |

ਚੱਕਰ ਦਾ ਆਰੰਭ ਸਰੀਰ ਦੇ ਹੇਠਲੇ ਹਿੱਸੇ ਤੋਂ ਹੋਵੇਗਾ | ਖੱਬੇ ਪੈਰ ਨੂੰ ਸੱਜੇ ਪਾਸੇ ਝੁਕਾਵਾਂਗੇ, ਸਰੀਰ ਦਾ ਭਾਰ ਇਸ ਦੇ ਉੱਪਰ ਆਵੇਗਾ ਸੱਜਾ ਗੋਡਾ ਵੀ ਨਾਲ ਹੀ ਘੁੰਮੇਗਾ, ਸੱਜਾ ਪੈਰ ਵੀ ਘੁੰਮੇਗਾ, ਨਾਲ ਹੀ ਲੱਕ, ਢਿੱਡ ਵੀ ਘੁੰਮੇਗਾ ਜੋ ਕਿ ਸੱਜੀ ਬਾਂਹ ਅਤੇ ਚੱਕੇ ਨੂੰ ਵੀ ਨਾਲ ਲਿਆਵੇਗਾ ! ਇਸ ਸਥਿਤੀ ਨਾਲ ਗੋਲੇ ਨੂੰ ਪਾਰ ਕਰਨ ਦੀ ਕਿਰਿਆ ਸ਼ੁਰੂ ਹੋਵੇਗੀ । ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਖੱਬਾ ਪੈਰ ਜ਼ਮੀਨ ਨੂੰ ਛੱਡੇਗਾ । ਇਸ ਦੇ ਬਾਅਦ ਖੱਬਾ ਪੈਰ ਚੁੱਕਾ ਸੁੱਟਣ ਦੀ ਹਾਲਤ ਵਿਚ ਅੱਗੇ ਵਧੇਗਾ । ਸੱਜਾ ਪੈਰ ਗੋਡੇ ਤੋਂ ਮੁੜਿਆ ਹੋਇਆ ਅਰਧ ਚੱਕਰ ਹੀ ਹਾਲਤ ਵਿਚ ਖੱਬੇ ਤੋਂ ਸੱਜੇ ਪਾਸੇ ਅੱਗੇ ਨੂੰ ਚੱਲੇਗਾ |

ਘੁੰਮਦੇ ਸਮੇਂ ਦੋਵੇਂ ਪੁੱਠੇ ਮੋਢੇ ਤੋਂ ਅੱਗੇ ਹੋਣਗੇ, ਜਿਸ ਨਾਲ ਸਰੀਰ ਦੇ ਉੱਪਰਲੇ ਹਿੱਸੇ ਅਤੇ ਹੇਠਾਂ ਦੇ ਹਿੱਸੇ ਵਿਚ ਮੋੜ ਪੈਦਾ ਹੋਵੇਗਾ । ਸੱਜੀ ਬਾਂਹ, ਜਿਸ ਵਿਚ ਚੱਕਾ ਹੋਵੇਗਾ, ਸਿਰ ਕੁਹਣੀ ਤੇ ਸਿੱਧਾ ਹੋਵੇਗਾ, ਖੱਬੀ ਬਾਂਹ ਕੁਹਣੀ ਤੋਂ ਮੁੜੀ ਹੋਈ ਸੀਨੇ ਦੇ ਸਾਹਮਣੇ ਹੋਵੇਗੀ । ਸਿਰ ਸਿੱਧਾ ਰਹੇਗਾ । ਸੱਜੇ ਪੈਰ ਦੇ ਪੰਜੇ ਤੇ ਜ਼ਮੀਨ ਤੋਂ ਥੋੜਾ ਰੱਖ ਕੇ ਗੋਲੇ ਨੂੰ ਪਾਰ ਕਰਾਂਗੇ ਤੇ ਸੱਜੇ ਪੈਰ ਦੇ ਪੰਜੇ ‘ਤੇ ਜ਼ਮੀਨ ਤੇ ਆਵਾਂਗੇ । ਇਹ ਪੈਰ ਲਗਪਗ ਕੇਂਦਰ ਵਿਚ ਆਵੇਗਾ | ਪੰਜਾ ਪਾਸੇ ਵਲ ਮੁੜਿਆ ਹੋਵੇਗਾ ।

ਢੰਗ
(METHODS)
ਇਸ ਵਿਚ ਮੁੱਖ ਰੂਪ ਵਿਚ ਹੇਠ ਲਿਖੀਆਂ ਤਿੰਨ ਵਿਧੀਆਂ ਹਨ –
1. ਸ਼ੁਰੂ ਕਰਦੇ ਸਮੇਂ ਵੀ ਜੋ ਨਵੇਂ ਸੁੱਟਣ ਵਾਲੇ ਹੁੰਦੇ ਹਨ, ਉਹ ਆਪਣਾ ਸੱਜਾ ਪੈਰ ਕੇਂਦਰ ਦੀ ਰੇਖਾ ‘ਤੇ ਅਤੇ ਖੱਬਾ ਪੈਰ 10 ਸੈਂ: ਮੀ: ਛੱਲੇ (Ring) ਤੋਂ ਪਿੱਛੇ ਰੱਖਦੇ ਹਨ ।

2. ਦੂਸਰਾ ਢੰਗ ਜਿਸ ਵਿਚ ਆਮ ਸੁੱਟਣ ਵਾਲੀ ਕੇਂਦਰੀ ਰੇਖਾ ਨੂੰ ਦੋਹਾਂ ਪੈਰਾਂ ਦੇ ਵਿਚਕਾਰ ਰੱਖਦੇ ਹਨ ।

3. ਤੀਸਰਾ ਇਹ ਸੁੱਟਣ ਵਾਲੇ ਜੋ ਖੱਬੇ ਪੈਰ ਨੂੰ ਕੇਂਦਰੀ ਰੇਖਾ ‘ਤੇ ਰੱਖਦੇ ਹਨ । ਇਸੇ ਤਰ੍ਹਾਂ ਗੋਲੇ ਦੇ ਵਿਚਕਾਰ ਆਉਂਦੇ ਸਮੇਂ ਤਿੰਨ ਤਰ੍ਹਾਂ ਨਾਲ ਪੈਰ ਨੂੰ ਰੱਖਦੇ ਹਨ ।
ਪਹਿਲਾਂ 3 ਵਜੇ ਦੀ ਸਥਿਤੀ ਵਿਚ, ਦੂਜਾ 10 ਵਜੇ ਦੀ ਸਥਿਤੀ ਵਿਚ, ਤੀਜਾ 12 ਵਜੇ ਦੀ ਸਥਿਤੀ ਵਿਚ ।

ਜਿਸ ਵਿਚ 12 ਵਜੇ ਦੀ ਸਥਿਤੀ ਸਭ ਤੋਂ ਉੱਤਮ ਮੰਨੀ ਗਈ ਹੈ ਕਿਉਂਕਿ ਇਸ ਵਿਚ ਸੱਜੇ ਪੈਰ ਤੇ ਘੱਟ ਘੁੰਮਣਾ ਪੈਂਦਾ ਹੈ ਅਤੇ ਅੱਗੇ ਮੋਢੇ ਨੂੰ ਖੋਣ ਤੋਂ ਰੋਕਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਸੱਜਾ ਪੈਰ ਜ਼ਮੀਨ ‘ਤੇ ਆਉਣ ਦੇ ਬਾਅਦ ਵੀ ਲਗਾਤਾਰ ਘੁੰਮਦਾ ਰਹੇਗਾ ਅਤੇ ਖੱਬਾ ਪੈਰਾਂ ਗੋਲੇ ਦੇ ਅਖ਼ੀਰ ਵਿਚ ਕੇਂਦਰ ਦੀ ਰੇਖਾ ਤੇ ਥੋੜਾ ਖੱਬੇ ਪਾਸੇ ਪੰਜੇ ਅਤੇ ਅੰਦਰਲੇ ਹਿੱਸੇ ਨੂੰ ਜ਼ਮੀਨ ਤੇ ਲੱਗਾ ਰਹਿਣ ਦੇਵੇਗਾ ।

ਆਖਰੀ ਚਰਨ (Last Step)-ਇਸ ਸਮੇਂ ਦੋਵੇਂ ਪੈਰ ਜ਼ਮੀਨ ਤੇ ਹੋਣਗੇ, ਲੱਕ ਘੁੰਮਦੀ ਹੋਈ ਦਸ਼ਾ ਵਿਚ ਪਿੱਛੇ ਨੂੰ ਝੁਕਿਆ ਹੋਇਆ ਹੋਵੇਗਾ, ਖੱਬਾ ਪੈਰ ਸਿੱਧਾ ਹੋਵੇਗਾ, ਸੱਜਾ ਪੈਰ ਗੋਡੇ ਤੋਂ ਮੁੜਿਆ ਹੋਇਆ ਹੋਵੇਗਾ, ਸੱਜਾ ਗੋਡਾ ਅਤੇ ਪੱਠੇ ਖੱਬੇ ਪਾਸੇ ਨੂੰ ਘੁੰਮਦੇ ਹੋਏ ਹੋਣਗੇ । ਖੱਬੀ ਬਾਂਹ ਉੱਪਰ ਵੱਲ ਖੁੱਲ੍ਹੇਗੀ, ਸੱਜੀ ਬਾਂਹ ਸਰੀਰ ਤੋਂ ਦੂਰ ਰੱਖਦੇ ਹੋਏ ਉੱਪਰ ਦੀ ਦਸ਼ਾ ਵਿਚ ਲਿਆਵਾਂਗੇ ।

ਸੁੱਟਣਾ (Throwing)-ਦੋਵੇਂ ਪੈਰ ਜੋ ਕਿ ਘੁੰਮ ਕੇ ਅੱਗੇ ਜਾ ਰਹੇ ਸਨ, ਇਸੇ ਵੇਲੇ ਮੋਢਿਆਂ ਤੋਂ ਸਿੱਧੇ ਹੋਣਗੇ । ਪੱਠੇ ਅੱਗੇ ਨੂੰ ਵਧਣਗੇ, ਮੋਢੇ ਅਤੇ ਧੜ ਆਪਣਾ ਘੁੰਮਣਾ ਅੱਗੇ

ਦੀ ਦਸ਼ਾ ਵਿਚ ਸਮਾਪਤ ਕਰ ਚੁੱਕੇ ਹੋਣਗੇ । ਖੱਬੀ ਬਾਂਹ ਅਤੇ ਮੋਢਾ ਅੱਗੇ ਘੁੰਮਣਾ ਬੰਦ ਕਰ ਕੇ ਇਕ ਥਾਂ ਤੇ ਰੁਕ ਜਾਣਗੇ । ਸੱਜੀ ਬਾਂਹ ਅਤੇ ਮੋਢਾ ਅੱਗੇ ਅਤੇ ਉੱਪਰ ਵਧੇਗਾ । ਦੋਹਾਂ ਪੈਰਾਂ ਦੇ ਪੰਜਿਆਂ ਤੇ ਸਰੀਰ ਦਾ ਭਾਰ ਹੋਵੇਗਾ ਅਤੇ ਦੋਵੇਂ ਪੈਰ ਸਿੱਧੇ ਹੋਣਗੇ ! ਅਖੀਰ ਵਿਚ ਖੱਬਾ ਪੈਰ ਪਿੱਛੇ ਆਵੇਗਾ, ਸੱਜਾ ਪੈਰ ਅੱਗੇ ਜਾ ਕੇ ਗੋਡੇ ਤੋਂ ਮੁੜੇਗਾ । ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਵੀ ਅੱਗੇ ਨੂੰ ਝੁਕਿਆ ਹੋਵੇਗਾ । ਅਜਿਹਾ ਸਰੀਰ ਦਾ ਸੰਤੁਲਨ ਬਣਾਈ ਰੱਖਣ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ !

ਸਾਧਾਰਨ ਨਿਯਮ
(GENERAL RULES)
ਚੱਕੇ (IDiscus) ਦਾ ਭਾਰ ਮਰਦ ਵਰਗ ਲਈ 2 ਕਿਲੋਗਰਾਮ, ਔਰਤ ਵਰਗ ਲਈ 1 ਕਿਲੋਗਰਾਮ ਹੁੰਦਾ ਹੈ । ਗੋਲੇ ਦਾ ਘੇਰਾ 2.5 ਮੀਟਰ ਹੁੰਦਾ ਹੈ ।ਵਰਤਮਾਨ ਸਮੇਂ ਵਿਚ ਚੱਕੇ ਦੇ ਗੋਲੇ ਦੇ ਬਾਹਰ ਲੋਹੇ ਦੀ ਕੇਜ (Cage) ਬਣਾਈ ਜਾਂਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਕਿ ਚੱਕੇ ਤੋਂ ਕਿਸੇ ਨੂੰ ਸੱਟ ਨਾ ਪੁੱਜੇ । ਸਾਹਮਣੇ 6 ਮੀਟਰ, ਹੋਰ 7 ਮੀਟਰ । ਇਹ ਅੰਗਰੇਜ਼ੀ ਦੇ C ਦੇ ਆਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਦੀ ਉੱਚਾਈ 3.35 ਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਸੈਕਟਰ 40 ਦਾ ਉਸੇ ਤਰ੍ਹਾਂ ਬਣਾਵਾਂਗੇ ਜਿਵੇਂ ਗੋਲੇ ਦੇ ਲਈ : ਹੋਰ ਸਾਰੇ ਨਿਯਮ ਗੋਲੇ ਦੀ ਤਰ੍ਹਾਂ ਹੀ ਇਸ ਵਿਚ ਕੰਮ ਆਉਣਗੇ ।

ਭਾਲਾ ਸੁੱਟਣਾ (JAVELIN THROW)

• ਜੈਵਲਿਨ ਦਾ ਭਾਰ = 800 ਗਾ, ਮਰਦਾਂ ਲਈ ਅਤੇ 640 ਗ੍ਰਾ. ਔਰਤਾਂ ਲਈ
• ਰਨਵੇ ਦੀ ਲੰਬਾਈ = 30 ਮੀ. ਤੋਂ 36.50 ਮੀ.
• ਰਨਵੇ ਦੀ ਚੌੜਾਈ = 4 ਮੀ.
• ਜੈਵਲਿਨ ਦੀ ਲੰਬੀ = 260 ਸੈਂ.ਮੀ ਤੋਂ 270 ਸੈਂ.ਮੀ.
  ਮਰਦਾਂ ਲਈ 220 ਸੈਂ.ਮੀ. ਤੋਂ
  230 ਸੈਂ. ਮੀ. ਔਰਤ ਲਈ ਦਾ ਕੌਣ : 8.95
  5 ਜੈਵਲਿਨ ਦੇ ਬਾਟਾ ਤੇ

ਭਾਲੇ ਨੂੰ ਸਿਰ ਦੇ ਬਰਾਬਰ ਉੱਚਾਈ ਤੇ ਕੰਨ ਦੇ ਕੋਲ, ਬਾਂਹ ਕੂਹਣੀ ਤੋਂ ਝੁਕੀ ਹੋਈ, ਕੂਹਣੀ ਅਤੇ ਜੈਵਲਿਨ ਦੋਹਾਂ ਦਾ ਮੂੰਹ ਸਾਹਮਣੇ ਵੱਲ ਹੋਵੇਗਾ । ਹੱਥ ਦੀ ਤਲੀ ਦਾ ਰੁੱਖ ਉੱਪਰ ਵਲ ਹੋਵੇਗਾ ! ਜ਼ਮੀਨ ਦੇ ਸਮਾਨਾਂਤਰ ਪੂਰੀ ਲੰਬਾਈ 30 ਤੋਂ 35 ਮੀ: ਹੋਵੇਗੀ । 3/4 ਦੌੜ ਪੱਖ ਵਿਚ ਸਿੱਧੇ ਜਾਂਗੇ । 1/3 ਆਖਰੀ ਹਿੱਸੇ ਵਿਚ ਪੰਜ ਕਦਮ ਦੇ ਲਗਪਗ ਕਰਾਸ ਸਟੈਂਪ (Cross Step) ਲਵਾਂਗੇ ।

ਆਖਰੀ ਚਰਨ ਵਿਚ ਜਦੋਂ ਖੱਬਾ ਪੈਰ ਪੜਤਾਲ ਚਿੰਨ੍ਹ (Check Mark) ‘ਤੇ ਆਵੇਗਾ, ਸੱਜਾ ਮੋਢਾ ਹੌਲੀ ਰਫ਼ਤਾਰ ਵਿਚ ਸੱਜੇ ਪਾਸੇ ਮੁੜਨਾ ਸ਼ੁਰੂ ਕਰੇਗਾ ਅਤੇ ਸੱਜੀ ਬਾਂਹ ਪਿੱਛੇ ਆਉਣਾ ਸ਼ੁਰੂ ਕਰੇਗੀ | ਕਦਮਾਂ ਦੇ ਵਿਚਕਾਰ ਦਾ ਫ਼ਾਸਲਾ ਵਧਣ ਲੱਗੇਗਾ । ਸੱਜਾ ਹੱਥ ਅਤੇ ਮੋਢਾ ਬਰਾਬਰ ਪਿੱਛੇ ਨੂੰ ਆਉਣਗੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਖੁੱਲਦੇ ਜਾਣਗੇ | ਲੱਕ ਅਤੇ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਪਿੱਛੇ ਵਲ ਝੁਕਦਾ ਜਾਵੇਗਾ । ਉੱਪਰਲੇ ਅਤੇ ਹੇਠਾਂ ਦੇ ਹਿੱਸੇ ਵਿਚ ਮੌੜ ਪੈਦਾ ਹੋਵੇਗਾ, ਕਿਉਂਕਿ ਉੱਪਰਲਾ ਹਿੱਸਾ ਜੇ ਪਾਸੇ ਵਲ ਖੁੱਲੇਗਾ ਅਤੇ ਹੇਠਲਾ ਹਿੱਸਾ ਸਿੱਧਾ ਅੱਗੇ ਨੂੰ ਤੁਰੇਗਾ ।
ਅੱਖਾਂ ਅੱਗੇ ਵੱਲ ਦੇਖਦੀਆਂ ਹੋਈਆਂ ਹੋਣਗੀਆਂ ।

ਅਖੀਰ ਵਿਚ ਸੱਜਾ ਪੈਰ ਗੋਡੇ ਤੋਂ ਲੁਕੀ ਹੋਈ ਹਾਲਤ ਵਿਚ ਜ਼ਮੀਨ ਤੇ ਕਰਾਸ ਸਟਾਪ ਦੇ ਅਖੀਰ ਵਿਚ ਆਵੇਗਾ । ਜਿਵੇਂ ਹੀ ਗੋਡਾ ਅੱਗੇ ਵਧੇਗਾ, ਸੱਜੇ ਪੈਰ ਦੀ ਗੱਡੀ ਜ਼ਮੀਨ ਤੋਂ ਉੱਪਰ ਉੱਠਣੀ ਸ਼ੁਰੂ ਹੋ ਜਾਵੇਗੀ । ਇਸ ਤਰ੍ਹਾਂ ਨਾਲ ਇਹ ਖੱਬੇ ਪੈਰ ਨੂੰ ਵਧੇਰੇ ਦੂਰੀ ‘ਤੇ ਜਾਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦੀ ਹੈ । ਆਖਰੀ ਦੌੜ-ਥਰੋ ਕਰਨ ਦੀ ਹਾਲਤ ਵਿਚ ਜਦੋਂ ਖੱਬਾ ਪੈਰ ਜ਼ਮੀਨ ਤੇ ਆਵੇਗਾ ਤਾਂ ਕੁਲਾ (Hip) ਅੱਗੇ ਵਧਣਾ ਸ਼ੁਰੂ ਕਰ ਦੇਵੇਗਾ । ਸੱਜਾ ਪੈਰ ਅਤੇ ਗੋਡਾ ਅੰਦਰ ਨੂੰ ਘੁੰਮੇਗਾ ਅਤੇ ਸਿੱਧਾ ਹੋ ਕੇ ਲੱਤ ਨੂੰ ਸਿੱਧਾ ਕਰੇਗਾ ਮੱਜੀ ਕੂਹਣੀ ਬਾਹਰ ਵਲ ਘੁੰਮੇਗੀ । ਖੱਬੇ ਪੈਰ ਦਾ ਰੁਕਣਾ ਸੱਜੇ ਪੈਰ ਨੂੰ ਘੁਮਾਉਣਾ ਅਤੇ ਸਿੱਧਾ ਕਰੇ ਸਭ ਨਾਲ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਧਨੁੱਖ ਦੀ ਤਰ੍ਹਾਂ ਪਿੱਛੇ ਨੂੰ ਝੁਕੇਗਾ ਅਤੇ ਸੀਨੇ ਅਤੇ ਢਿੱਡ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਵਿਚ ਤਣਾਅ ਪੈਦਾ ਹੋਵੇਗਾ । ਸੁੱਟਣ ਦੇ ਬਾਅਦ ਫਾਉਲ ਬਚਾਉਣ ਲਈ ਸਰੀਰ ਦੇ ਭਾਰ ਨੂੰ ਕੰਟਰੋਲ ਵਿਚ ਰੱਖਣ ਲਈ ਕਦਮ ਵਿਚ ਤਬਦੀਲੀ ਲਿਆਵਾਂਗੇ ! ਸੱਜਾ ਪੈਰ ਅੱਗੇ ਜਾ ਕੇ ਗੋਡੇ ਤੇ ਮੁੜੇਗਾ, ਪੰਜਾ ਖੱਬੇ ਪਾਸੇ ਨੂੰ ਝੁਕੇਗਾ । ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਹਿੱਸਾ ਸੱਜੇ ਤੋਂ ਅੱਗੇ ਨੂੰ ਝੁਕ ਤੇ ਸੰਤੁਲਨ ਬਣਾਵੇਗਾ । ਸੱਚਾ ਪੈਰ ਆਪਣੀ ਥਾਂ ਤੋਂ ਉੱਠ ਕੇ ਕੁੱਝ ਅੱਗੇ ਵੀ ਵਧ ਸਕਦਾ ਹੈ |

ਪ੍ਰਸ਼ਨ 9.
ਜੈਵਲਿਨ ਥਰੋ ਦੇ ਨਿਯਮ ਲਿਖੋ ।
ਉੱਤਰ –

ਸਾਧਾਰਨ ਨਿਯਮ
(GENERAL RULES)

1. ਮਰਦ ਦੇ ਭਾਲੇ ਦੀ ਲੰਬਾਈ 2.60 ਮੀ: ਤੋਂ 2.70 ਮੀ:, ਔਰਤਾਂ ਦੇ ਭਾਲੇ ਦੀ ਲੰਬਾਈ 2.20 ਮੀ: ਤੋਂ 2.30 ਮੀ: ।
2. ਭਾਲਾ ਸੁੱਟਣ ਲਈ ਘੱਟੋ-ਘੱਟ 30.5 ਮੀ: ਵੱਧ ਤੋਂ ਵੱਧ 35.50 ਮੀ: ਲੰਮਾ ਅਤੇ 4 ਮੀ: ਚੌੜਾ ਰਸਤਾ ਚਾਹੀਦਾ ਹੈ । ਸਾਹਮਣੇ 70 ਮਿ: ਮੀ: ਦੀ ਚਾਪ ਵਕਰ ਆਕਾਰ ਸਫੈਦ ਲੋਹੇ ਦੀ ਪੱਟੀ ਹੋਵੇਗੀ, ਜੋ ਕਿ ਦੋਵੇਂ ਪਾਸੇ 75 ਸੈਂ: ਮੀ: ਨਿਕਲੀ ਰਹੇਗੀ । ਇਸ ਨੂੰ ਸਫੈਦ ਚੂਨੇ ਨਾਲ ਵੀ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ । ਇਹ ਰੇਖਾ 8 ਮੀ: ਸੈਂਟਰ ਤੋਂ ਖਿੱਚੀ ਜਾ ਸਕਦੀ ਹੈ ।
3. ਭਾਲੇ ਦਾ ਸੈਕਟਰ 29° ਦਾ ਹੁੰਦਾ ਹੈ, ਜਿੱਥੇ ਕਰਾਕਾਰ ਰੇਖਾ ਮਿਲਦੀ ਹੈ, ਉੱਥੇ ਹੀ ਨਿਸ਼ਾਨ ਲਗਾ ਦਿੰਦੇ ਹਨ |
   ਪੂਰਨ ਤੌਰ ‘ਤੇ ਸਹੀ ਕੋਣ ਲਈ 40 ਮੀ: ਦੀ ਦੁਰੀ ਤੋਂ ਦੋਹਾਂ ਭੁਜਾਵਾਂ ਦੇ ਵਿਚਕਾਰ ਦੀ ਦੂਰੀ 20 ਮੀ: ਹੋਵੇਗੀ, 60 ਮੀ: ਦੀ ਦੂਰੀ ਤੇ 30 ਮੀ: ਹੋਵੇਗੀ ।

4. ਭਾਲਾ ਸਿਰਫ ਵਿਚਕਾਰੋਂ ਫੜਨ (Gip) ਦੀ ਥਾਂ ਤੋਂ ਹੀ ਫੜ ਕੇ ਸੁੱਟਣਗੇ । ਭਾਲੇ ਦਾ ਅਗਲਾ ਹਿੱਸਾ ਜ਼ਮੀਨ ਤੇ ਲੱਗਣਾ ਚਾਹੀਦਾ ਹੈ |
ਸਰੀਰ ਦੇ ਕਿਸੇ ਹਿੱਸੇ ਤੋਂ 50 ਸੈਂ. ਮੀ. | ਚੌੜੀਆਂ ਦੋਵੇਂ ਪਾਸੇ ਦੀਆਂ ਰੇਖਾਵਾਂ ਨੂੰ ਜਾਂ ਅੱਗੇ 70 ਸੈਂ. ਮੀ. ਚੌੜੀ ਰੇਖਾ ਨੂੰ ਛੂਹ ਜਾਣ ਨੂੰ ਫਾਊਲ ਥਰੋ (Foul Throw) ਮੰਨਾਂਗੇ ।

5. ਸ਼ੁਰੂ ਕਰਨ ਤੋਂ ਅੰਤ ਤਕ ਭਾਲਾ ਸੁੱਟਣ ਦੀ ਕਲਾ ਵਿਚ ਰਹੇਗਾ । ਭਾਲੇ ਨੂੰ ਚੱਕਰ ਕੱਟ ਕੇ ਨਹੀਂ ਸੁੱਟਣਗੇ । ਸਿਰਫ ਮੋਢੇ ਤੇ ਉੱਪਰੋਂ ਸੁੱਟ ਸਕਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਰਿਲੇਅ ਦੌੜਾਂ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? ਲਿਖੋ ।
ਉੱਤਰ –
ਰਿਲੇਅ ਦੌੜ
(RELAY RACES)

ਪੁਰਸ਼ (Men)	ਅਰਤਾਂ (Women)
4 x 100 ਮੀਟਰ	4 x 100 ਮੀਟਰ
4 x 200 ਮੀਟਰ	4 x 400 ਮੀਟਰ
4 x 400 ਮੀਟਰ

ਮੈਡਲੇ ਰਿਲੇਅ ਦੌੜ
(MEDLEY RELAY RACE)

ਬੈਟਨ (Baton)-ਸਾਰੀਆਂ ਗੋਲਾਕਾਰ ਰਿਲੇਅ ਦੌੜਾਂ ਵਿਚ ਬੈਟਨ ਨੂੰ ਲੈ ਜਾਣਾ ਹੁੰਦਾ ਹੈ । ਬੈਟਨ ਇਕ ਖੋਖਲੀ ਨਲੀ ਦਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਇਸਦੀ ਲੰਬਾਈ 30 ਸੈਂ: ਮੀ: ਤੋਂ ਵੱਧ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ । ਇਸਦਾ ਘੇਰਾ 12 ਸੈਂਟੀਮੀਟਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਭਾਰ 50 ਗਰਾਮ ਤੋਂ ਵੱਧ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ।

ਰਿਲੇਅ ਦੌੜ ਪੱਥ (Relay Race Track)-ਰਿਲੇਅ ਦੌੜ ਪੱਥ ਪੁਰੇ ਚੱਕਰ ਦੇ ਲਈ ਛੋਟੇ ਰਾਹਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾਂ ਅੰਕਿਤ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਜੋ ਅਜਿਹਾ ਸੰਭਵ ਨਹੀਂ ਹੈ , ਤਾਂ ਘੱਟ ਤੋਂ ਘੱਟ ਬੈਟਨ ਵਿਨਿਯ ਖੇਤਰ ਤੰਗ ਰਾਹਾਂ ਵਿਚ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਰਿਲੇਅ ਦੌੜ ਦਾ ਆਰੰਭ (Start of Relay Race)-ਦੌੜ ਦੇ ਆਰੰਭ ਵਿਚ ਬੈਟਨ ਦਾ ਕੋਈ ਵੀ ਹਿੱਸਾ ਮੁੱਢਲੀ ਰੇਖਾ ਤੋਂ ਅੱਗੇ ਨਿਕਲ ਸਕਦਾ ਹੈ ਪਰ ਬੈਟਨ ਰੇਖਾ ਜਾਂ ਅੱਗੇ ਦੀ ਜ਼ਮੀਨ ਨੂੰ ਨਹੀਂ ਛੂਹਦਾ ।

ਬੈਟਨ ਲੈਣਾ (Taking the Baton)-ਬੈਟਨ ਲੈਣ ਲਈ ਵੀ ਖੇਤਰ ਮਿੱਥਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਖੇਤਰ ਦੌੜ ਦੀ ਮਿੱਥੀ ਦੂਰੀ ਰੇਖਾ ਦੇ ਦੋਵੇਂ ਪਾਸੇ 10 ਮੀਟਰ ਲੰਮੀ ਰੋਕ ਰੇਖਾ ਖਿੱਚ ਕੇ . ਨਿਸ਼ਾਨ ਲਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਬੈਟਨ ਲੈਣ ਜਾਂ ਦੇਣ ਲਈ 20 ਮੀਟਰ ਲੰਮਾ ਇਕ ਕਮਰਾ ਜਿਹਾ ਬਣ ਜਾਂਦਾ ਹੈ । 4 x 200 ਮੀਟਰ ਤਕ ਦੀਆਂ ਰਿਲੇਅ ਦੌੜਾਂ ਪਹਿਲੇ ਦੌੜਾਕ ਦੇ ਇਲਾਵਾ ਟੀਮ ਦੇ ਹੋਰ ਮੈਂਬਰ ਬੈਟਨ ਲੈਣ ਲਈ ਮਿੱਥੇ ਖੇਤਰ ਦੇ ਬਾਹਰ ਪਰ 10 ਮੀਟਰ ਤੋਂ ਘੱਟ ਦੂਰੀ ਤੋਂ ਦੌੜਨਾ ਸ਼ੁਰੂ ਕਰਦੇ ਹਨ ।

ਬੈਟਨ ਵਿਨਿਮਯ (Exchange of Baton)-ਬੈਟਨ ਵਿਨਿਯਮ ਮਿੱਥੇ ਖੇਤਰ ਦੇ ਅੰਦਰ ਹੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਧੱਕਣ ਜਾਂ ਕਿਸੇ ਵੀ ਤਰ੍ਹਾਂ ਸਹਾਇਤਾ ਕਰਨ ਦੀ ਆਗਿਆ ਨਹੀਂ ਹੈ । ਦੌੜਾਕ ਇਕ ਦੂਜੇ ਨੂੰ ਬੈਟਨ ਨਹੀਂ ਸੁੱਟ ਸਕਦੇ । ਜੇ ਬੈਟਨ ਡਿੱਗ ਪੈਂਦਾ ਹੈ, ਤਾਂ ਇਸ ਨੂੰ ਡੇਗਣ ਵਾਲਾ ਦੌੜਾਕ ਹੀ ਉਠਾਵੇਗਾ ।