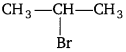Class 12 – Page 21 – PSEB Solutions

PSEB 12th Class History Book Solutions Guide in Punjabi English Medium

August 13, 2024August 12, 2024 by Prasanna

Punjab State Board Syllabus PSEB 12th Class History Book Solutions Guide Pdf in English Medium and Punjabi Medium are part of PSEB Solutions for Class 12.

PSEB 12th Class History Guide | History Guide for Class 12 PSEB

History Guide for Class 12 PSEB | PSEB 12th Class History Book Solutions

PSEB 12th Class History Book Solutions in English Medium

PSEB 12th Class History Book Solutions in Hindi Medium

PSEB 12th Class History Book Solutions in Punjabi Medium

Map Question Topics
In this part there will be one question on the map. The question on the map will be compulsory. The question of Map will be set out of the following Map of Punjab.
1. Battles of Guru Gobind Singh Ji.
2. Important Battles of Banda Singh Bahadur.
3. Ranjit Singh’s Kingdom.
4. First Anglo-Sikh War.
5. Second Anglo-Sikh War.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4

August 9, 2024August 8, 2024 by Bhagya

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3 Matrices Ex 3.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.4

Direction (1 – 17) Using elementary transformations, find the inverse of each of the matrices.

Question 1.
\(\left[\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 1

Question 2.
\(\left[\begin{array}{ll}
2 & 1 \\
1 & 1
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & 1
\end{array}\right]\)

We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 2

Question 3.
\(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 7
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 3

Question 4.
\(\left[\begin{array}{ll}
2 & 3 \\
5 & 7
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ll}
2 & 3 \\
5 & 7
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 4

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 5

Question 5.
\(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
Solution.
\(\left[\begin{array}{ll}
2 & 1 \\
7 & 4
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 6

Question 6.
\(\left[\begin{array}{ll}
2 & 5 \\
1 & 3
\end{array}\right]\)
Solution.
Let A = \left[\begin{array}{ll}
2 & 5 \\
1 & 3
\end{array}\right]
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 7

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 8

Question 7.
\(\left[\begin{array}{ll}
\mathbf{3} & 1 \\
5 & 2
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ll}
\mathbf{3} & 1 \\
5 & 2
\end{array}\right]\)

We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 9

Question 8.
\(\left[\begin{array}{ll}
4 & 5 \\
3 & 4
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ll}
4 & 5 \\
3 & 4
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 10

Question 9.
\(\left[\begin{array}{cc}
3 & 10 \\
2 & 7
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{cc}
3 & 10 \\
2 & 7
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 11

Question 10.
\(\left[\begin{array}{cc}
3 & -1 \\
-4 & 2
\end{array}\right]\)
Solution.
\(\left[\begin{array}{cc}
3 & -1 \\
-4 & 2
\end{array}\right]\)
We know that A = IA.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 12

Question 11.
\(\left[\begin{array}{rr}
2 & -6 \\
1 & -2
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{rr}
2 & -6 \\
1 & -2
\end{array}\right]\)
We know that A = IA.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 13

Question 12.
\(\left[\begin{array}{cc}
6 & -3 \\
-2 & 1
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{cc}
6 & -3 \\
-2 & 1
\end{array}\right]\)
We know that A = IA.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 14

Now, in the above equation, we can see all the zeroes in the second law of the matrix on the L.H.S.
Threrefore, A^-1 does not exist.

Question 13.
\(\left[\begin{array}{cc}
\mathbf{2} & -\mathbf{3} \\
-1 & 2
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{cc}
\mathbf{2} & -\mathbf{3} \\
-1 & 2
\end{array}\right]\)

We know that A = IA.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 15

⇒ \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]=\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right] A\) (applying R₁ → R₁ + R₂)

∴ A^-1 = \(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\)

Question 14.
\(\left[\begin{array}{ll}
2 & 1 \\
4 & 2
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ll}
2 & 1 \\
4 & 2
\end{array}\right]\)
We know that A = IA
∴ \(\left[\begin{array}{ll}
2 & 1 \\
4 & 2
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right] A\)

Applying R₁ → R₁ – \(\frac{1}{2}\) R₂, we have
\(\left[\begin{array}{ll}
0 & 0 \\
4 & 2
\end{array}\right]=\left[\begin{array}{rr}
1 & -\frac{1}{2} \\
0 & 1
\end{array}\right] A\)

Now, in the above equation, we can see all the zeroes in the first row of the matrix on the L.H.S.
Therefore, A^-1 does not exist.

Question 15.
\(\left[\begin{array}{rrr}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
Solution.
let A = \(\left[\begin{array}{rrr}
2 & -3 & 3 \\
2 & 2 & 3 \\
3 & -2 & 2
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 16

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 17

Question 16.
\(\left[\begin{array}{ccc}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & 3 & -2 \\
-3 & 0 & -5 \\
2 & 5 & 0
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 18

Question 17.
\(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
We know that A = IA

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.4 19

Question 18.
Matrices A and B will be inverse of each other only if
(A) AB = BA
(B) AB = BA = 0
(C) AB = 0,BA = I
(D) AB = BA = I
Solution.
We know that if A is a square matrix of order m, and if there exists another square matrix B of the same order m, such that AB = BA = I, then B is said to be the inverse of A.
In this case, it is clear that A is the inverse of B.
Thus, matrices A and B will be inverse of each other only if AB = BA = I. Hence, the correct answer is (D).

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5

August 9, 2024August 8, 2024 by Bhagya

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.5

Direction (1 – 2): Find adjoint of each of the matrices.

Question 1.
\(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ll}
1 & 2 \\
3 & 4
\end{array}\right]\)
We have,
A₁₁ = 4, A₁₂ = – 3, A₂₁ = – 2, A₂₂ = 1
∴ adj(A) = \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]^{T}=\left[\begin{array}{rr}
4 & -3 \\
-2 & 1
\end{array}\right]^{T}=\left[\begin{array}{cc}
4 & -2 \\
-3 & 1
\end{array}\right]\).

Question 2.
\(\left[\begin{array}{ccc}
1 & -1 & 2 \\
2 & 3 & 5 \\
-2 & 0 & 1
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
2 & 3 & 5 \\
-2 & 0 & 1
\end{array}\right]\)
We have, A₁₁ = \(\left|\begin{array}{ll}
3 & 5 \\
0 & 1
\end{array}\right|\) = 3 – 0 = 3

A₁₂ = \(-\left|\begin{array}{cc}
2 & 5 \\
-2 & 1
\end{array}\right|\) = -(2 + 10) = – 12

A₁₃ = \(\left|\begin{array}{cc}
2 & 3 \\
-2 & 0
\end{array}\right|\) = 0 + 6 = 6

A₂₁ = \(-\left|\begin{array}{cc}
-1 & 2 \\
0 & 1
\end{array}\right|\) = -(- 1 – 0) = 1

A₂₂ = \(\left|\begin{array}{cc}
1 & 2 \\
-2 & 1
\end{array}\right|\) = 1 + 4 = 5

A₂₃ = \(-\left|\begin{array}{cc}
1 & -1 \\
-2 & 0
\end{array}\right|\) = – (0 – 2) = 2

A₃₁ = \(\left|\begin{array}{cc}
-1 & 2 \\
3 & 5
\end{array}\right|\) = – 5 – 6 = – 11

A₃₂ = \(-\left|\begin{array}{ll}
1 & 2 \\
2 & 5
\end{array}\right|\) = – (5 – 4) = – 1

A₃₃ = \(\left|\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right|\) = 3 + 2 = 5.

Direction (3 – 4): Verify A(adj A) = (adj A)A = |A| I.

Question 3.
\(\left[\begin{array}{cc}
2 & 3 \\
-4 & -6
\end{array}\right]\)
Sol.
Let A = \(\left[\begin{array}{cc}
2 & 3 \\
-4 & -6
\end{array}\right]\), |A| = \(\left|\begin{array}{rr}
2 & 3 \\
-4 & -6
\end{array}\right|\)
= – 12 – (- 12) = – 12 + 12 = 0
|A| = – 12 – (- 12) = – 12 + 12 = 0
∴ |A| = \(0\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)
Now, A₁₁ = – 6, A₁₂ = 4, A₂₁ = – 3, A₂₂ = 2
∴ adj (A) = \(\left[\begin{array}{cc}
-6 & -3 \\
4 & 2
\end{array}\right]\)

Now, A (adj A) = \(\left[\begin{array}{cc}
2 & 3 \\
-4 & -6
\end{array}\right]\left[\begin{array}{cc}
-6 & -3 \\
4 & 2
\end{array}\right]\)

= \(\left[\begin{array}{cc}
-12+12 & -6+6 \\
24-24 & 12-12
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)

Also, (adj A) A = \(\left[\begin{array}{cc}
-6 & -3 \\
4 & 2
\end{array}\right]\left[\begin{array}{cc}
2 & 3 \\
-4 & -6
\end{array}\right]\)

= \(\left[\begin{array}{cc}
-12+12 & -18+18 \\
8-8 & 12-12
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)

Hence, A (adj A) = (adj A) A = |A| I.

Question 4.
\(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\)
Now, |A| = 1 (0 – 0) + 1 (9 + 2) + 2 (0 – 0) = 11

∴ |A| I = \(11\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]=\left[\begin{array}{ccc}
11 & 0 & 0 \\
0 & 11 & 0 \\
0 & 0 & 11
\end{array}\right]\)

Now, A₁₁ = 0, A₁₂ = – (9 + 2) = – 11, A₁₃ = 0
A₂₁ = – (- 3 – 0) = 3, A₂₂ = 3 – 2 = 1, A₂₃ = – (0 + 1) = – 1
A₃₁ = 2 – 0 = 2, A₃₂ = – (- 2 – 6) = 8, A₃₃ = 0 + 3 = 3

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 1

Direction (5 – 11): Find the inverse of the matrices (if it exists).

Question 5.
\(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)

We have, |A| = \(\left|\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right|\) = 6 – (- 8) = 14
Cofactors of A are
A₁₁ = 3,
A₁₂ = – 4,
A₂₁ = 2,
A₂₂ = 2

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 2

(Note: If determinant of any matrix is zero, then its inverse does not exist.)

Question 6.
\(\left[\begin{array}{cc}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{cc}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
We have, |A| = \(\) = – 2 + 15 = 13
Now, Cofactors of A are
A = 2,
A = 3,
A = – 5,
A = – 1
adj (A) = \(\left[\begin{array}{rr}
2 & -5 \\
3 & -1
\end{array}\right]\)

A^-1 = \(\frac{1}{|A|}\) (adj A)
= \(\frac{1}{13}\left[\begin{array}{cc}
2 & -5 \\
3 & -1
\end{array}\right]=\left[\begin{array}{cc}
\frac{2}{13} & -\frac{5}{13} \\
\frac{3}{13} & -\frac{1}{13}
\end{array}\right]\)

Question 7.
\(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)

We have, |A| = 1 (10 – 0) – 2 (0 – 0) + 3 (0 – 0)= 10
Cofactors of A are
A₁₁ = 10 – 0 =10,
A₁₂ = – (0 – 0) = 0,
A₁₃ = 0 – 0 = 0
A₂₁ = – (10 – 0) = – 10,
A₂₂ = 5 – 0 = 5,
A₂₃ = – (0 – 0) = 0
A₃₁ = 8 – 6 = 2,
A₃₂ = – (4 – 0) = – 4,
A₃₃ = 2 – 0 = 2

∴ adj (A) = \(\left[\begin{array}{ccc}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right]\)

A^-1 = \(\frac{1}{|A|}\) (adj A)

= \(\frac{1}{10}\left[\begin{array}{ccc}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right]=\left[\begin{array}{ccc}
1 & -1 & \frac{1}{5} \\
0 & \frac{1}{2} & -\frac{2}{5} \\
& 0 & \frac{1}{5}
\end{array}\right]\)

Question 8.
\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)
We have, |A| = 1 (- 3 – 0) – 0 + 0 = – 3
Cofactors of A are
A₁₁ = – 3 – 0 = – 3
A₁₂ = – (- 3 – 0) = 3
A₁₃ = 6 – 15 = – 9
A₂₁ = – (0 – 0) = 0
A₂₂ = – 1 – 0 = – 1
A₂₃ = – (2 – 0) = – 2
A₃₁ = 0 – 0 = 0
A₃₂ = – (0 – 0) = 0
A₃₃ = 3 – 0 = 3

∴ adj(A) = \(\left[\begin{array}{ccc}
-3 & 0 & 0 \\
3 & -1 & 0 \\
-9 & -2 & 3
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{|A|}\) (adj A)

= \(-\frac{1}{3}\left[\begin{array}{ccc}
-3 & 0 & 0 \\
3 & -1 & 0 \\
-9 & -2 & 3
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
-1 & \frac{1}{3} & 0 \\
& \frac{2}{3} & -1
\end{array}\right]\)

Question 9.
\(\left[\begin{array}{ccc}
2 & 1 & 3 \\
4 & -1 & 0 \\
-7 & 2 & 1
\end{array}\right]\)
Solution.
\(\left[\begin{array}{ccc}
2 & 1 & 3 \\
4 & -1 & 0 \\
-7 & 2 & 1
\end{array}\right]\)

We have, |A| = 2 (- 1 – 0) – 1 (4 – 0) + 3 (8 – 7)
= 2 (- 1) – 1 (4) + 3(1)
= – 2 – 4 + 3 = – 3
Cofactors of A are
A₁₁ = – 1 – 0 = – 1,
A₁₂ = – (4 – 0) = – 4,
A₁₃ = 8 – 7 = 1
A₂₁ = – (1 – 6) = 5,
A₂₂ = 2 + 21 = 23,
A₂₃ = – (4 + 7) = – 11
A₃₁ = 0 + 3 = 3,
A₃₂ = – (0 – 12) = 12,
A₃₃ = – 2 – 4 = – 6

∴ adj (A) = \(\left[\begin{array}{ccc}
-1 & 5 & 3 \\
-4 & 23 & 12 \\
1 & -11 & -6
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{|A|}\) (adj A)
= \(-\frac{1}{3}\left[\begin{array}{ccc}
-1 & 5 & 3 \\
-4 & 23 & 12 \\
1 & -11 & -6
\end{array}\right]=\left[\begin{array}{ccc}
\frac{1}{3} & -\frac{5}{3} & -1 \\
\frac{4}{3} & -\frac{23}{3} & -4 \\
-\frac{1}{3} & \frac{11}{3} & 2
\end{array}\right]\)

Question 10.
\(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\)

We have, |A| = 1(8 – 6) – 0 + 3 (3 – 4) = 2 – 3 = – 1
Cofactors of A are
A₁₁ = 8 – 6 = 2
A₁₂ = – (0 + 9) = – 9
A₁₃ = 0 – 6 = – 6
A₂₁ = – (- 4 + 4) = 0,
A₂₂ =4 – 6 = – 2,
A₂₃ = – (- 2 + 3) = – 1
A₃₁ = 3 – 4 = – 1,
A₃₂ = – (- 3 – 0)= 3,
A₃₃ = 2 – 0 = 2
∴ adj (A) = \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
-9 & -2 & 3 \\
-6 & -1 & 2
\end{array}\right]\)
∴ A^-1 = \(\frac{1}{|A|}\) adj (A)
= \(\frac{1}{-1}\left[\begin{array}{ccc}
2 & 0 & -1 \\
-9 & -2 & 3 \\
-6 & -1 & 2
\end{array}\right]=\left[\begin{array}{ccc}
-2 & 0 & 1 \\
9 & 2 & -3 \\
6 & 1 & -2
\end{array}\right]\)

Question 11.
\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \alpha & \sin \alpha \\
0 & \sin \alpha & -\cos \alpha
\end{array}\right]\)
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \alpha & \sin \alpha \\
0 & \sin \alpha & -\cos \alpha
\end{array}\right]\)

We have, |A| = 1(- cos² α – sin² α)
= – (cos² α + sin² α) = – 1
Cofactors of A are
A₁₁ = – cos² α – sin² α = – 1,
A₁₂ = 0,
A₁₃ = 0,
A₂₁ = 0,
A₂₂ = – cos α,
A₂₃ = – sin α
A₃₁ = 0,
A₃₂ = – sin α,
A₃₃ = cos α

∴ adj (A) = \(\left[\begin{array}{ccc}
-1 & 0 & 0 \\
0 & -\cos \alpha & -\sin \alpha \\
0 & -\sin \alpha & \cos \alpha
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{|A|}\) (adj A)
= \(=\frac{1}{-1}\left[\begin{array}{ccc}
-1 & 0 & 0 \\
0 & -\cos \alpha & -\sin \alpha \\
0 & -\sin \alpha & \cos \alpha
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \alpha & \sin \alpha \\
0 & \sin \alpha & -\cos \alpha
\end{array}\right]\)

Question 12.
Let A = \(\left[\begin{array}{ll}
3 & 7 \\
2 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
6 & 8 \\
7 & 9
\end{array}\right]\). verify that (AB)^-1 = B^-1 A^-1
Solution.
Let A = \(\left[\begin{array}{ll}
3 & 7 \\
2 & 5
\end{array}\right]\)
We have, |A| = 15 – 14 = 1
Cofactors of A are
A₁₁ = 5,
A₁₂ = – 2,
A₂₁ = – 7,
A₂₂ = 3
∴ adj (A) = \(\left[\begin{array}{cc}
5 & -7 \\
-2 & 3
\end{array}\right]\)

∴ A = \(\frac{1}{|A|}\) (adj A)
= \(\frac{1}{1}\left[\begin{array}{cc}
5 & -7 \\
-2 & 3
\end{array}\right]\)

Now, let B = \(\left[\begin{array}{ll}
6 & 8 \\
7 & 9
\end{array}\right]\)
We have, |B| = 54 – 56 = – 2
Cofactors of B are
B₁₁ = 9,
B₁₂ = – 7,
B₂₁ = – 8,
B₂₂ = 6

∴ adj (B) = \(\left[\begin{array}{cc}
9 & -8 \\
-7 & 6
\end{array}\right]\)

∴ B^-1 = \(\frac{1}{|B|}\) adj (B)
\(-\frac{1}{2}\left[\begin{array}{cc}
9 & -8 \\
-7 & 6
\end{array}\right]=\left[\begin{array}{cc}
-\frac{9}{2} & 4 \\
\frac{7}{2} & -3
\end{array}\right]\)

Now, B^-1A^-1 = \(\left[\begin{array}{cc}
-\frac{9}{2} & 4 \\
\frac{7}{2} & -3
\end{array}\right]\left[\begin{array}{cc}
5 & -7 \\
-2 & 3
\end{array}\right]\)

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 3

From Eqs. (i) and (ii), we have
(AB)^-1 = B^-1 A^-1
Hence, the given result is proved.

Question 13.
If A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\), show that A² – 5A + 7 I = 0. Hence find A^-1.
Solution.

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 4

∵ |A| = \(\left|\begin{array}{rr}
3 & 1 \\
-1 & 2
\end{array}\right|\)
= 6 + 1 = 7 ≠ 0
∴ A^-1 exists.
Hence, A² – 5A + 7I = 0.
∴ A . A – 5A = – 7I
⇒ A . A(A^-1) – 5AA^-1 = – 7IA^-1 [multiplying by A^-1 on both sides]
⇒ A(AA^-1) – 5I = – 7A^-1
⇒ AI – 5I = – 7A^-1
⇒ A^-1 = \(\frac{1}{7}\) (A – 5I)
= \(\frac{1}{7}\left(\left[\begin{array}{cc}
5 & 0 \\
0 & 5
\end{array}\right]-\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\right)=\frac{1}{7}\left[\begin{array}{cc}
2 & -1 \\
1 & 3
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{7}\left[\begin{array}{cc}
2 & -1 \\
1 & 3
\end{array}\right]\)

Question 14.
For a matrix A \(\left[\begin{array}{ll}
3 & 2 \\
1 & 1
\end{array}\right]\), find the numbers a and b such that A² + aA + bI = 0.
Solution.

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 5

If two matrices are equal, then their corresponding elements are equal.
11 + 3a + b = 0 ………….(i)
8 + 2a = 0 …….(ii)
4 + a = 0 ………..(iii)
and 3 + a + b = 0 …………..(iv)
Solving Eqs. (iii) and (iv), we get
4 + a
⇒ a = – 4
and 3 + a + b = 0
⇒ 3 – 4 + b = 0
⇒ b = 1
Thus, a = – 4 and b = 1.

Question 15.
For the matrix A = \(\left[\begin{array}{ccc}
\mathbf{1} & \mathbf{1} & \mathbf{1} \\
\mathbf{1} & \mathbf{2} & -\mathbf{3} \\
\mathbf{2} & -\mathbf{1} & \mathbf{3}
\end{array}\right]\), show that A³ – 6A² + 5A + 11I = 0. Hence, find A^-1.
Solution.
Given, A = \(\left[\begin{array}{ccc}
\mathbf{1} & \mathbf{1} & \mathbf{1} \\
\mathbf{1} & \mathbf{2} & -\mathbf{3} \\
\mathbf{2} & -\mathbf{1} & \mathbf{3}
\end{array}\right]\)

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 6

Now, A³ – 6A² + 5A + 11I = 0
⇒ (AAA)A^-1 – 6(AA)A^-1 + 5AA^-1 +11IA^-1 = 0
[Pre-multiplying by A^-1 as |A| ≠ 0]
⇒ AA(AA^-1) – 6A(AA^-1) + 5(AA^-1) = -11(IA^-1)
⇒ A² – 6A + 5I = – 11A^-1
⇒ A^-1 = – \(\frac{1}{11}\) (A² – 6A + 5I) …………(i)
Now, A² – 6A + 5I

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 7

= \(\left[\begin{array}{ccc}
9 & 2 & 1 \\
-3 & 13 & -14 \\
7 & -3 & 19
\end{array}\right]-\left[\begin{array}{ccc}
6 & 6 & 6 \\
6 & 12 & -18 \\
12 & -6 & 18
\end{array}\right]=\left[\begin{array}{ccc}
3 & -4 & -5 \\
-9 & 1 & 4 \\
-5 & 3 & 1
\end{array}\right]\)

From eq. (i), we have

A^-1 = \(-\frac{1}{11}\left[\begin{array}{ccc}
3 & -4 & -5 \\
-9 & 1 & 4 \\
-5 & 3 & 1
\end{array}\right]=\frac{1}{11}\left[\begin{array}{ccc}
-3 & 4 & 5 \\
9 & -1 & -4 \\
5 & -3 & -1
\end{array}\right]\)

Question 16.
If A = \(\left[\begin{array}{ccc}
2 & -1 & 1 \\
-1 & 2 & -1 \\
1 & -1 & 2
\end{array}\right]\), then verify that A³ – 6A² + 9A – 4I = 0 and hence, find A^-1.
Solution.

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 8

∴ A³ – 6A² + 9A – 4I = 0
⇒ (AAA) A^-1 – 6(AA)A^-1 + 9 AA^-1 – 4 IA^-1 = 0
[pre-multiplying by A^-1 as |A| ≠ 0]
⇒ AA(AA^-1) – 6 A(AA^-1) + 9 (AA^-1) = 4(IA^-1)
⇒ AAI – 6AI + 9 I = 4A^-1
⇒ A² – 6A + 9I = 4 A^-1
⇒ A^-1 = \(\frac{1}{4}\) (A² – 6A +9I)
Now, A² – 6A +9I
= \(\left[\begin{array}{ccc}
6 & -5 & 5 \\
-5 & 6 & -5 \\
5 & -5 & 6
\end{array}\right]-6\left[\begin{array}{ccc}
2 & -1 & 1 \\
-1 & 2 & -1 \\
1 & -1 & 2
\end{array}\right]+9\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
6 & -5 & 5 \\
-5 & 6 & -5 \\
5 & -5 & 6
\end{array}\right]-\left[\begin{array}{ccc}
12 & -6 & 6 \\
-6 & 12 & -6 \\
6 & -6 & 12
\end{array}\right]+\left[\begin{array}{ccc}
9 & 0 & 0 \\
0 & 9 & 0 \\
0 & 0 & 9
\end{array}\right]=\left[\begin{array}{ccc}
3 & 1 & -1 \\
1 & 3 & 1 \\
-1 & 1 & 3
\end{array}\right]\)

From Eq. (i) we have A^-1 = \(\frac{1}{4}\) \(\left[\begin{array}{ccc}
3 & 1 & -1 \\
1 & 3 & 1 \\
-1 & 1 & 3
\end{array}\right]\)

Question 17.
Let A be a non-singular square matrix of order 3 x 3. Then,
Ia4jAIIs equal to
(A) A
(B) A²
(C) A³
(D) 3|A|
Solution.
We know that,

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 9

Hence, the correct answer is (B).

Question 18.
If A is an invertible matrix of order 2, then det (A’) is equal to
(A) det |A|
(B) \(\frac{1}{\ det (A)}\)
(C) 1
(D) 0
Solution.
Since, A is an invertible matrix. So, A^-1 exists and A^-1 = \(\frac{1}{|A|}\) adj (A).

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.5 10

Hence, the correct answer is (B).

PSEB 12th Class Physical Education Solutions Chapter 5 ਅਸਮਰਥਾ

August 9, 2024August 8, 2024 by Bhagya

Punjab State Board PSEB 12th Class Physical Education Book Solutions Chapter 5 ਅਸਮਰਥਾ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physical Education Chapter 5 ਅਸਮਰਥਾ

Physical Education Guide for Class 12 PSEB ਅਸਮਰਥਾ Textbook Questions and Answers

ਇੱਕ ਅੰਕ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (One Mark Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਅਸਮਰਥਾ ਦਾ ਕੀ ਅਰਥ ਹੈ ?
ਉੱਤਰ-
ਅਮਰਥਾ ਦਾ ਅਰਥ ਹੈ, ਕੋਈ ਵਿਸ਼ੇਸ਼ ਸਰੀਰਕ ਜਾਂ ਮਾਨਸਿਕ ਕੰਮ ਕਰਨ ਦੀ ਅਯੋਗਤਾ । ਜਦੋਂ ਸਰੀਰਕ ਮਾਨਸਿਕ ਕਾਰਜ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਘੱਟ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇਸ ਅਵਸਥਾ ਨੂੰ ਅਸਮਰਥਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਮਾਜਿਕ ਪੁਨਰਵਾਸ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸਮਾਜਿਕ ਪੁਨਰ-ਵਿਸਥਾਪਨ (Social Rehabilitation) – ਇਸ ਨਾਲ ਅਸਮਰਥ ਵਿਅਕਤੀ ਦੇ ਪਰਿਵਾਰਕ ਅਤੇ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਬਹਾਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਉਸਦੀ ਅਸਮਰਥਾ ਦੇ ਬਾਵਜੂਦ ਉਸਦੇ ਸਮਾਜਿਕ ਰੁਤਬੇ ਨੂੰ ਹੁਲਾਰਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਅੰਨਿਆਂ ਲਈ ਉਦਯੋਗਿਕ ਘਰ ਕਿੱਥੇ ਹਨ ?
ਉੱਤਰ-
ਅੰਨਿਆਂ ਲਈ ਉਦਯੋਗਿਕ ਘਰ (Industrial Home for Blind) – 1971 ਵਿੱਚ ਬਣਾਈ ਗਈ ਇਹ ਸੰਸਥਾ ਮੁੰਬਈ ਵਿਚ ਸਥਿਤ ਹੈ ਅਤੇ ਇੱਥੇ ਅੰਨ੍ਹੇ ਬੱਚਿਆਂ ਨੂੰ ਕਿੱਤਾ ਅਗਵਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ਤਾਂ ਜੋ ਉਹ ਅਸਮਰਥ ਹੋਣ ਦੇ ਬਾਵਜੂਦ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਖ਼ੁਦ ਕਰ ਸਕਣ ।

ਦੋ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Two Marks Question Answers)

ਪ੍ਰਸ਼ਨ 4.
ਸਥਾਈ ਅਯੋਗਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਸ ਅਯੋਗਤਾ ਵਿਚ ਵਿਅਕਤੀ ਕਿਸੇ ਤਰ੍ਹਾਂ ਕੰਮ ਨਹੀਂ ਕਰ ਸਕਦਾ ਅਤੇ ਇਹ ਲੰਬੇ ਸਮੇਂ ਜਾਂ ਜੀਵਨ ਭਰ ਠੀਕ ਨਹੀਂ ਹੁੰਦੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਰਿਆਤਮਕ ਅਸਮਰਥਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਸ ਕਿਸਮ ਦੀ ਅਸਮਰਥਾ ਵਿਚ ਸਰੀਰਕ ਅੰਗ ਪ੍ਰਭਾਵਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਹ ਨੁਕਸ ਆਮ ਕਰਕੇ ਲੰਬੀ ਬਿਮਾਰੀਆਂ ਕਾਰਨ ਹੁੰਦੇ ਹਨ । ਸਾਹ ਦੀ ਬਿਮਾਰੀ, ਸਿੱਲੀਕੋਸਿਸ, ਐਸਬੈਗਸ, ਲੀਡ ਕਹਿਰ, ਸਾਈਡਰੋਸਿਸ, ਬਾਈਸਨੋਸਿਸ, ਲੇਬਰੋਸਿਸ, ਲੰਗ ਕੈਂਸਰ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਥਾਈ ਅਯੋਗਤਾ ਅਤੇ ਅਸਥਾਈ ਅਯੋਗਤਾ ਵਿੱਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ-

ਸਥਾਈ ਅਯੋਗਤਾ (Permanent Disability) – ਇਸ ਅਯੋਗਤਾ ਵਿਚ ਵਿਅਕਤੀ ਕਿਸੇ ਤਰ੍ਹਾਂ ਕੰਮ ਨਹੀਂ ਕਰ ਸਕਦਾ ਅਤੇ ਇਹ ਲੰਬੇ ਸਮੇਂ ਜਾਂ ਜੀਵਨ ਭਰ ਠੀਕ ਨਹੀਂ ਹੁੰਦੀ ।
ਅਸਥਾਈ ਅਯੋਗਤਾ (Temporary Disability) – ਇਹ ਕੁਝ ਸਮੇਂ ਲਈ ਹੁੰਦੀ ਹੈ ਅਤੇ ਵਿਅਕਤੀ ਕੰਮਕਾਰ ਕਰ ਸਕਦਾ ਹੈ । ਕੁਝ ਮੁੜ-ਵਸੇਬੇ ਪ੍ਰੋਗਰਾਮਾਂ ਨਾਲ ਵਿਅਕਤੀ ਠੀਕ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਅਸਮਰਥਾ ਤੋਂ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਕੋਈ ਦੋ ਕਾਰਨਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-

ਮਾਨਸਿਕ ਤੱਤ (Mental Factor) – ਮਾਨਸਿਕ ਅਸਮਰਥਾ ਕਦੇ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ਪਰ ਕਈ ਵਾਰ ਇਹ ਮਾਨਸਿਕ ਤਨਾਅ ਕਾਰਨ ਵੀ ਹੋ ਸਕਦੀ ਹੈ । ਮਨ ਅਤੇ ਸਰੀਰ ਆਪਸ ਵਿਚ ਸੰਬੰਧਿਤ ਹੁੰਦੇ ਹਨ । ਇਸ ਲਈ ਮਾਨਸਿਕ ਤੱਤ ਸਰੀਰਕ ਸਥਿਤੀ ਨੂੰ ਬੁਰੀ ਤਰ੍ਹਾਂ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ ।
ਸਰੀਰਕ ਬਿਮਾਰੀ (Physical Disease) – ਸਰੀਰਕ ਬਿਮਾਰੀ ਜਾਂ ਬਿਮਾਰੀਆਂ ਦੇ ਕਾਰਨ ਕੁਝ ਕਮੀਆਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਜੋ ਕਿ ਅਸਮਰਥਾ ਦਾ ਕਾਰਨ ਬਣਦੀਆਂ ਹੈ ; ਜਿਵੇਂ ਕਿ ਚੇਚਕ ਦੀ ਬਿਮਾਰੀ ਕਾਰਨ ਅੰਨਾਪਨ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਅਸੀਂ ਇਹ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਰੀਰਕ ਬਿਮਾਰੀ ਅਸਮਰਥਾ ਦਾ ਕਾਰਨ ਹੋ ਸਕਦੀ ਹੈ ।

ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Three Marks Question Answers)

ਪ੍ਰਸ਼ਨ 8.
ਕਿੱਤਿਆਂ ਤੋਂ ਪੈਦਾ ਹੋਣ ਵਾਲੀਆਂ ਅਸਮਰਥਾਵਾਂ ਦੇ ਕਾਰਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਬਹੁਤ ਸਾਰੀਆਂ ਅਸਮਰਥਾਵਾਂ ਕੰਮ ਕਰਨ ਵਾਲੇ ਮਾਹੌਲ ਵਿਚ ਹੁੰਦੀਆਂ ਹਨ । ਜਿਵੇਂ ਕਿ ਸਾਹ ਦੀ ਅਸਮਰਥਾ, ਜ਼ਹਿਰੀਲੇ ਪਦਾਰਥ ਹਵਾ ਦੁਆਰਾ ਸਰੀਰ ਵਿਚ ਜਾਣ ਨਾਲ ਹੋ ਸਕਦੀ ਹੈ । ਜਿਵੇਂ ਕਿ ਐਸਬੈਮਟੋਲ | ਫਾਇਬਰਜ਼ ਦੇ ਸਾਹ ਦੁਆਰਾ ਅੰਦਰ ਜਾਣ ਨਾਲ ਐਸਬੈਟਿਸਸ ਨਾਮਕ ਬਿਮਾਰੀ ਦਾ ਕਾਰਨ ਬਣਦਾ ਹੈ । ਕਈ ਵਾਰ ਸਰੀਰ ਦੀ ਗਲਤ ਸਥਿਤੀ (Postural) ਜਿਵੇਂ ਕਿ ਗਲਤ ਬੈਠਕ, ਖੜ੍ਹੇ ਹੋਣ ਦੀ ਸਥਿਤੀ ਜਾਂ ਗਲਤ ਝੁਕਾਅ ਦੀਆਂ ਆਦਤਾਂ ਨਾਲ ਅਪੰਗਤਾ ਹੋ ਜਾਂਦੀ ਹੈ । ਉਦਾਹਰਨ ਵਜੋਂ ਕਾਈਫੋਸਿਸ (ਕੁੱਬਾਪਣ ਦਰਜ਼ੀਆਂ ਵਿਚ ਆਮ ਦੇਖਣ ਨੂੰ ਮਿਲਦਾ ਹੈ । ਕਿੱਤਾ ਸੰਬੰਧਿਤ ਕਈ ਅਸਮਰਥਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

1. ਭੌਤਿਕ ਕਾਰਨ (Physical Factor) – ਬਹੁਤ ਸਾਰੀਆਂ ਅਯੋਗਤਾਵਾਂ ਭੌਤਿਕ ਕਾਰਨਾਂ ਜਿਵੇਂ ਕਿ ਗਰਮੀ, ਸਰਦੀ, ਰੋਸ਼ਨੀ, ਦਬਾਅ, ਰੌਲਾ, ਵਿਕੀਰਣਾਂ (Radiations) ਆਦਿ ਨਾਲ ਵਾਪਰਦੀਆਂ ਹਨ । ਮਿਸਾਲ ਵਜੋਂ-ਅੰਤ ਦਾ ਠੰਡਾ ਮੌਸਮ ਫੁੱਟ ਬਾਈਟ (ਪੈਰ ਗਲ ਜਾਣਾ) ਅਤੇ ਉੱਚਾ ਤਾਪਮਾਨ, ਹੀਟ ਕਰੇਮਪ, ਅਜਿਹੀਆਂ ਅਸਮਰਥਾਵਾਂ ਨੂੰ ਜਨਮ ਦਿੰਦੇ ਹਨ । ਕੰਮ ਦੇ ਸਥਾਨ ਤੇ ਉੱਚੀਆਂ ਅਵਾਜ਼ਾਂ ਜਾਂ ਰੌਲੇ ਕਾਰਨ ਬੋਲਾਪਣ ਹੋ ਸਕਦਾ ਹੈ ।

2. ਸਮਾਜਿਕ ਕਾਰਨ (Social Factor) – ਬਹੁਤ ਸਾਰੀਆਂ ਸਮਾਜਿਕ ਅਪਾਹਜਤਾ ਕੰਮ ਕਰਨ ਵਾਲਿਆਂ ਵਿਚ ਉਦੋਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਜਦ ਉਹ ਸਮਾਜਿਕ ਵਾਤਾਵਰਣ ਵਿਚ ਆਪਣੇ ਆਪ ਨੂੰ ਢਾਲ ਨਹੀਂ ਪਾਉਂਦੇ । ਇਹ ਕਈ ਵਾਰ ਆਪਣੇ-ਆਪ (Introvert) ਸੁਭਾਅ ਦੇ ਵਿਅਕਤੀਆਂ ਵਿਚ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਉਹ ਕੰਮ ਕਰਤਾ ਜੋ ਆਪਣੇ ਆਪ ਨੂੰ ਸਮਾਜ ਅਨੁਸਾਰ ਨਾ ਢਾਲ ਸਕੇ ਤਾਂ ਕਈ ਪ੍ਰੇਸ਼ਾਨੀਆਂ ਜਿਵੇਂ ਕਿ ਉਦਾਸੀ, ਤਣਾਅ, ਚਿੰਤਾ ਅਤੇ ਅਸੁਰੱਖਿਆ ਦੇ ਹੇਠ ਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੇ ਹੋਰ ਵੀ ਕਾਰਨ ਹਨ ਜਿਵੇਂ ਕਿ ਆਪਣੇ ਆਪ ਵਿਚ ਰਹਿਣਾ ਆਤਮਵਿਸ਼ਵਾਸ ਦੀ ਕਮੀ ਅਤੇ ਬੁਰੇ ਰਿਸ਼ਤੇ ਆਦਿ ।

3. ਰਸਾਇਣਿਕ ਤੱਤ (Chemical Factor) – ਕਈ ਅਸਮਰਥਾਵਾਂ ਰਸਾਇਣਿਕ ਪ੍ਰਦੂਸ਼ਣ ਨਾਲ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਰਸਾਇਣਿਕ ਪ੍ਰਦੂਸ਼ਣ, ਜਿਵੇਂ ਕਿ ਕਾਰਬਨ ਡਾਈਆਕਸਾਈਡ ਵਰਗੀਆਂ ਜ਼ਹਿਰੀਲੀਆਂ ਗੈਸਾਂ ਨਾਲ ਫੈਲਦਾ ਹੈ । ਇਸ ਨਾਲ ਲਗਾਤਾਰ ਸਿਰ ਦਰਦ ਅਤੇ ਸਾਹ ਰੁਕਣਾ ਆਦਿ ਬਿਮਾਰੀਆਂ ਲੱਗ ਸਕਦੀਆਂ ਹਨ । ਇਹ ਜ਼ਿਆਦਾਤਰ ਖਾਣਾਂ ਵਿਚ ਵਾਪਰਦਾ ਹੈ । ਹੋਰ ਜ਼ਹਿਰੀਲੀਆਂ ਗੈਸਾਂ ਜਿਵੇਂ ਕਾਰਬਨਡਾਈਆਕਸਾਈਡ, ਸਲਫਰਡਾਈਆਕਸਾਈਡ ਅਤੇ ਕਾਰਬਨ ਬਾਈਸਲਫਾਈਡ ਆਦਿ । ਇਹ ਗੈਸਾਂ ਕੰਮ ਕਰਨ ਵਾਲਿਆਂ ਦੁਆਰਾ ਸਾਹ ਲੈਣ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚੋਂ ਜਾ ਕੇ ਪਾਚਨ ਕ੍ਰਿਆ ਵਿਚ ਦਾਖਿਲ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਸਥਾਈ ਅਪੰਗਤਾ ਨੂੰ ਜਨਮ ਦਿੰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਸੇ ਇੱਕ ’ਤੇ ਨੋਟ ਲਿਖੋ ।
(ਉ) ਐੱਥਰਾਕੋਸਿਸ
(ਆ) ਸ਼ੀਸ਼ੇ ਦਾ ਜ਼ਹਿਰ
(ਇ) ਕੈਂਸਰ ਅਤੇ ਦਮਾ
(ਸ) ਮੁੱਢਲੀ ਸਹਾਇਤਾ ।
ਉੱਤਰ-
(ਉ) ਐੱਥਰਾਕੋਸਿਸ-ਇਹ ਨਾਮ ਐਂਥਕ ਸ਼ਬਦ ਜਿਸ ਦਾ ਭਾਵ ਹੈ ਕੋਇਲਾ ਜਾਂ ਕਾਰਬਨ ਅਤੇ ਉਸਸਿਸ ਦਾ ਅਰਥ ਪ੍ਰਸਥਿਤੀ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਬਿਮਾਰੀ ਉਹਨਾਂ ਲੋਕਾਂ ਵਿਚ ਆਮ ਪਾਈ ਜਾਂਦੀ ਹੈ ਜੋ ਕੋਇਲੇ ਦੀਆਂ ਖਾਨਾਂ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ । ਇਹ ਬਿਮਾਰੀ ਸਾਹ ਪ੍ਰਣਾਲੀ ਦੇ ਅੰਗਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਜਿਵੇਂ ਕਿ ਸਾਹ ਨਲੀ, ਫੇਫੜਿਆਂ ਅਤੇ ਨੱਕ ਦੀ ਨਲੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ । ਕੰਮ ਕਰਨ ਦੀ ਥਾਂ ‘ਤੇ ਕੋਇਲੇ ਦੇ ਕਣਾਂ ਨੂੰ ਸਾਹ ਦੁਆਰਾ ਅੰਦਰ ਲੈ ਜਾਣ ਨਾਲ ਫੇਫੜਿਆਂ ‘ਤੇ ਬੁਰਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਸ ਬਿਮਾਰੀ ਨੂੰ ਕਾਲੇ ਫੇਫੜੇ (Black lung) ਦੇ ਨਾਮ ਨਾਲ ਹੀ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ ।

(ਅ) ਸ਼ੀਸ਼ੇ ਦਾ ਜ਼ਹਿਰ-ਇਹ ਇਕ ਜ਼ਹਿਰੀਲੀ ਧਾਤੂ ਹੈ ਜੋ ਕਿ ਮਨੁੱਖ ਦੀ ਸਿਹਤ ‘ਤੇ ਬੁਰਾ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ । ਇਹ ਬਿਮਾਰੀ ਉਹਨਾਂ ਕਰਮਚਾਰੀਆਂ ਵਿਚ ਆਮ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿ ਨਿਰਮਾਣ ਕੰਮ ਜਿਵੇਂ ਕਿ ਪੇਟਿੰਗ, ਇਮਾਰਤ ਬਣਾਉਣਾ ਜਾਂ ਚੀਨੀ ਮਿੱਟੀ ਨਾਲ ਸੰਬੰਧਿਤ ਕੰਮ ਕਰਦੇ ਹਨ । ਇਹ ਸ਼ੀਸ਼ੇ ਦੇ ਕਣਾਂ ਨੂੰ ਸਾਹ ਦੁਆਰਾ ਸ਼ੀਸ਼ੇ ਨੂੰ ਸਰੀਰ ਦੇ ਅੰਦਰ ਲੈ ਜਾਣ ਨਾਲ ਬੁਰਾ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ । ਸ਼ੀਸ਼ੇ ਦੇ ਜ਼ਹਿਰ ਨਾਲ ਪ੍ਰਭਾਵਿਤ ਵਿਅਕਤੀ ਵਿਚ ਆਮ ਲੱਛਣ ਢਿੱਡ ਵਿਚ ਦਰਦ, ਬੇਹੋਸ਼ੀ, ਸਿਰ ਵਿਚ ਦਰਦ, ਸਰੀਰ ਵਿਚ ਦਰਦ, ਅੜਕਣ ਅਤੇ ਅਧਰੰਗ ਤੇ ਫੇਫੜਿਆਂ ਆਦਿ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਸ਼ਾਮਿਲ ਹਨ ।

(ਇ) ਕੈਂਸਰ ਅਤੇ ਦਮਾ-ਇਹ ਬਿਮਾਰੀ ਉਹਨਾਂ ਕਰਮਚਾਰੀਆਂ ਵਿਚ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿ ਰਸਾਇਣਿਕ ਤੱਤ, ਧੂੜ ਕਣ, ਕਿਰਨਾਂ ਦੇ ਸੰਪਰਕ ਵਿਚ ਵੱਧ ਰਹਿੰਦੇ ਹਨ । ਕੈਂਸਰ ਬਿਮਾਰੀ ਦੀ ਸੰਭਾਵਨਾ ਕੋਇਲੇ ਜਾਂ ਧਾਤੂ ਦੀਆਂ ਫੈਕਟਰੀਆਂ ਵਿਚ ਕੰਮ ਕਰਨ ਵਾਲੇ ਕਰਮਚਾਰੀਆਂ ਵਿਚ ਵੱਧ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਇਹਨਾਂ ਫੈਕਟਰੀਆਂ ਵਿਚ ਕੰਮ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਵਿਚ ਚਮੜੀ, ਫੇਫੜਿਆਂ ਜਾਂ ਖੁਨ ਨਾਲ ਸੰਬੰਧਿਤ ਕੈਂਸਰ ਵਿਕਸਿਤ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਕੋਇਲੇ ਦੀ ਖਾਨ, ਧੂੜ ਕਣ, ਫਰਨੈਂਸ ਅਤੇ ਰਸਾਇਣਿਕ ਤੱਤਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਕਰਮਚਾਰੀਆਂ ਵਿਚ ਫੇਫੜਿਆਂ ਨਾਲ ਸੰਬੰਧਿਤ ਬਿਮਾਰੀ ਜਿਵੇਂ ਕਿ ਦਮਾ ਜਾਂ ਬੋਈਟਾਈਸ ਹੋ ਸਕਦੀ ਹੈ ।

(ਸ) ਮੁੱਢਲੀ ਸਹਾਇਤਾ-ਮੁੱਢਲੀ ਸਹਾਇਤਾ ਡਾਕਟਰ ਦੇ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਤੁਰੰਤ ਦਿੱਤੀ ਜਾਣ ਵਾਲੀ ਸਹਾਇਤਾ ਹੁੰਦੀ ਹੈ । ਇਹ ਵਿਵਹਾਰਕ ਤੌਰ ਤੇ ਹੋਰ ਸੱਟਾਂ ਨੂੰ ਰੋਕਣਾ, ਮਰੀਜ਼ ਦੇ ਦਰਦ ਨੂੰ ਘਟਾਉਣਾ ਅਤੇ ਉਸਨੂੰ ਸੱਟ ਦੇ ਸਦਮੇ ਵਿਚੋਂ ਬਾਹਰ ਕੱਢਣ ਵਿਚ ਮੱਦਦ ਕਰਦੀ ਹੈ । ਮੁੱਢਲੀ ਸਹਾਇਤਾ ਦਾ ਮੂਲ ਸੰਕਲਪ ਖੂਨ ਵਗਣ ਤੋਂ ਰੋਕਣਾ, ਸਾਹ ਲੈਣ ਵਿਚ ਮੱਦਦ ਕਰਨਾ ਅਤੇ ਇਲਾਜ ਕਰਨ ਤੋਂ ਹੈ । ਮੁੱਢਲੀ ਸਹਾਇਤਾ ਵਿਚ ਇਹ ਯਕੀਨੀ ਬਣਾਉਣਾ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਮਰੀਜ਼ ਦਾ ਸਾਹ ਰਸਤਾ ਖੁੱਲਾ ਹੈ ਅਤੇ ਉਹ ਚੰਗੀ ਤਰ੍ਹਾਂ ਸਾਹ ਲੈ ਰਿਹਾ ਹੈ । ਉਸਦਾ ਖੂਨ ਦੌਰਾ ਜਿਵੇਂ ਨਾੜੀ ਗਤੀ, ਚਮੜੀ ਦਾ ਰੰਗ, ਬੇਕਾਬੁ ਖੂਨ ਵੱਗਣਾ ਆਦਿ ਠੀਕ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਅਗੁਰ ਮਰੀਜ਼ ਸਥਿਰ ਹੈ ਤਾਂ ਹੋਰਨਾਂ ਸੱਟਾਂ ਜਿਵੇਂ ਕਿ ਕੱਟਣਾ, ਸੱਜਣਾ ਜਾਂ ਹੱਡੀ ਟੁੱਟਣਾ ਦੀ ਸੰਭਾਲ ਮੁੱਢਲੀ ਸਹਾਇਤਾ ਵਿਚ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕੁੱਝ ਬੁਨਿਆਦੀ ਸੰਕਲਪ ਜਿਵੇਂ ਖੂਨ ਨੂੰ ਵੱਗਣ ਤੋਂ ਰੋਕਣਾ ਜਾਂ ਟੁੱਟੀਆਂ ਹੱਡੀਆਂ ਨੂੰ ਤਦ ਤਕ ਸਥਿਰ ਰੱਖਣਾ ਜਦ ਤਕ ਉਹਨਾਂ . ਦਾ ਮੁੱਲਾਂਕਣ ਨਹੀਂ ਕੀਤਾ ਜਾਂਦਾ ਜਾਂ ਫਿਰ ਜੋੜ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ, ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਜ਼ਰੂਰੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਭਾਰਤ ਰੈੱਡ ਕਰਾਸ ਸੁਸਾਇਟੀ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਇਹ ਇੱਕ ਰਾਸ਼ਟਰੀ ਅਦਾਰਾ ਹੈ ਜੋ ਕਿ ਅੰਤਰਰਾਸ਼ਟਰੀ ਰੈੱਡ ਕਾਸ ਸੁਸਾਇਟੀ ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ । ਰੈੱਡ ਕਾਸ ਨੂੰ ਬਿਮਾਰਾਂ ਅਤੇ ਜ਼ਖ਼ਮੀਆਂ ਨੂੰ ਬਚਾਉਣ ਦਾ ਪ੍ਰਤੀਕ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਇੰਟਰਨੈਸ਼ਨਲ ਰੈੱਡ ਖ਼ਾਸ ਸੁਸਾਇਟੀ ਸੰਨ 1863 ਵਿੱਚ ਜੇ.ਐੱਸ. ਦੁਨੰਤ ਦੁਆਰਾ ਸਥਾਪਿਤ ਕੀਤੀ ਗਈ ਸੀ ਅਤੇ ਇੰਡੀਅਨ ਰੈੱਡ ਖ਼ਾਸ ਸੁਸਾਇਟੀ 1920 ਵਿੱਚ ਹੋਂਦ ਵਿੱਚ ਆਈ । ਇਸ ਦੇ ਭਿੰਨ ਮੰਤਵ ਹਨ- ਸਿਹਤ ਵਿੱਚ ਸੁਧਾਰ, ਬਿਮਾਰੀਆਂ ਤੋਂ ਬਚਾਉ ਅਤੇ ਬਿਮਾਰੀ ਦੀ ਗੰਭੀਰਤਾ ਨੂੰ ਘਟਾਉਣਾ । ਰੈੱਡ ਕਾਸ ਜੰਗ ਦੇ ਦਿਨਾਂ ਦੌਰਾਨ ਵੀ ਮਦਦ ਕਰਦਾ ਹੈ। ਇਹ ਥੈ-ਸੇਵੀ ਸੰਸਥਾ, ਭੂਚਾਲ, ਹੜ੍ਹ ਅਤੇ ਤੂਫ਼ਾਨਾਂ ਸਮੇਂ ਜ਼ਖ਼ਮੀ ਹੋਏ ਲੋਕਾਂ ਨੂੰ ਖਾਣ ਵਾਲੀਆਂ ਚੀਜ਼ਾਂ ਅਤੇ ਦਵਾਈਆਂ ਵੀ ਵੰਡਦਾ ਹੈ । ਇੰਡੀਅਨ ਰੈੱਡ ਕਾਸ ਸੁਸਾਇਟੀ ਦੀਆਂ ਭਾਰਤ ਵਿੱਚ 400 ਤੋਂ ਵੱਧ ਸ਼ਾਖਾਵਾਂ ਹਨ । ਇਹ ਫ਼ੌਜੀਆਂ ਦੀ ਵੀ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ । ਬੰਗਲੌਰ ਵਿੱਚ ਇਸ ਦਾ ਇੱਕ ਬਹੁਤ ਵੱਡਾ ਹਸਪਤਾਲ ਹੈ ।ਇੰਡੀਅਨ ਰੈਂਡ ਫ਼ਾਸ ਸੁਸਾਇਟੀ ਦੀ ਸੈਂਟ ਜੌਹਨ ਐਂਬੂਲੈਂਸ ਐਸੋਸੀਏਸ਼ਨ ਵੀ ਹੈ ਜਿਸ ਨੇ ਹਜ਼ਾਰਾਂ ਲੋਕਾਂ ਨੂੰ ਫਸਟ ਏਡ ਅਤੇ ਨਰਸਿੰਗ ਦੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਹੈ ।

ਪੰਜ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Five Marks Question Answers)

ਪ੍ਰਸ਼ਨ 11.
ਮੁੜ-ਵਸੇਬੇ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਇਸ ਬਾਰੇ ਪੂਰੀ ਜਾਣਕਾਰੀ ਦਿਉ ।
ਉੱਤਰ-
ਪੁਨਰ-ਵਿਸਥਾਪਨ ਦਾ ਅਰਥ ਅਤੇ ਪਰਿਭਾਸ਼ਾ (Meaning and Definition of Rehabilitation) – ਸ਼ਬਦ ‘ਰੀਹੈਬਲੀਟੇਸ਼ਨ’’ ਸ਼ਬਦ ਹੈਬੀਲਿਟਾਂ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ ਜਿਸਦਾ ਅਰਥ ਹੈ ਸਮਰੱਥਾ । ਇਸ ਲਈ ਪੁਨਰ ਵਿਸਥਾਪਨ ਦਾ ਅਰਥ ਹੈ ‘ਮੁੜ ਕਬਜ਼ਾ’ । ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿਚ ਪੁਨਰਵਿਸਥਾਪਨ ਦਾ ਅਰਥ ਹੈ ‘‘ਪਹਿਲੀ ਤੰਦਰੁਸਤੀ ਪ੍ਰਾਪਤ ਕਰਨਾ ਜਾਂ ਰਾਜ਼ੀ ਹੋਣਾ ਅਤੇ ਟਿਕ ਜਾਣਾ ।

ਡਬਲਯੂ. ਐੱਚ. ਓ. (W.H.O.) ਦੇ ਅਨੁਸਾਰ, “ਪੁਨਰ ਵਿਸਥਾਪਨ, ਅਸਮਰਥ ਵਿਅਕਤੀ ਵਿਚ ਕੰਮ ਕਰਨ ਦੀ ਉਚਤਮ ਯੋਗਤਾ ਪੈਦਾ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਹਿੱਤ ਉਸਦੀ ਪੁਨਰਸਿਖਲਾਈ ਲਈ ਡਾਕਟਰੀ, ਸਮਾਜਿਕ, ਵਿੱਦਿਅਕ ਅਤੇ ਕਿੱਤਾਕਾਰੀ ਢੰਗਾਂ ਦੀ ਸਮੁੱਚੀ ਅਤੇ ਸੰਯੁਕਤ ਵਰਤੋਂ ਹੈ । ਉਦਾਹਰਨ ਵਜੋਂ ਇਕ ਵਿਅਕਤੀ ਕਿਸੇ ਸੱਟ ਨਾਲ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਗੁਆ ਬੈਠਦਾ ਹੈ । ਉਸਦੀ ਤੰਦਰੁਸਤੀ ਨੂੰ ਵਾਪਿਸ ਲਿਆਉਣ ਲਈ ਕੀਤੇ ਕੰਮ ਪੁਨਰ ਵਿਸਥਾਪਨ ਅਖਵਾਉਂਦਾ ਹੈ । ਪੁਰਾਣੇ ਸਮਿਆਂ ਵਿੱਚ ਅਸਮਰਥ ਵਿਅਕਤੀ ਨੂੰ ਸਮਾਜ ਵਲੋਂ ਅਣਗੌਲਾ ਕਰ ਦਿੱਤਾ ਜਾਦਾ ਸੀ ਪਰੰਤੂ ਅੱਜਕੱਲ੍ਹ ਅਸਮਰਥ ਨੂੰ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਵਿਚ ਵਾਪਸ ਲਿਆਉਣ ਲਈ ਕੀਤੇ ਕੰਮਾਂ ਨੂੰ ਪੁਨਰਵਿਸਥਾਪਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਅਪਾਹਜਾਂ ਨੂੰ ਕਿੱਤਾਕਾਰੀ ਦੀ ਸਿਖਲਾਈ ਵੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਸਿੱਖਿਆ ਨੂੰ ਕਿੱਤਾਕਾਰੀ ਸਿਖਲਾਈ (Vocational training) ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪੁਨਰ-ਵਿਸਥਾਪਨ ਦਾ ਖੇਤਰ (Scope for Rehabilitation) – ਪੁਨਰ-ਵਿਸਥਾਪਨ ਦਾ ਖੇਤਰ ਬਹੁਤ ਹੀ ਵਿਸ਼ਾਲ ਹੈ । ਕਿਉਂਕਿ ਦੁਰਘਟਨਾਵਾਂ ਕਾਰਨ ਪੁਨਰ ਵਿਸਥਾਪਨ ਦੀ ਲੋੜ ਮਹਿਸੂਸ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਪੁਨਰ-ਵਿਸਥਾਪਨ ਦੇ ਖੇਤਰ ਨੂੰ ਹੇਠ ਲਿਖੇ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ-

ਡਾਕਟਰੀ ਪੁਨਰ-ਵਿਸਥਾਪਨ (Medical Rehabilitation) – ਕਿਸੇ ਸੱਟ ਜਾਂ ਬਿਮਾਰੀ ਨਾਲ ਆਏ ਕਿਸੇ ਸਰੀਰਕ ਵਿਗਾੜ ਦੀ ਸੂਰਤ ਵਿਚ ਮਾਹਿਰ ਡਾਕਟਰੀ ਸਹਾਇਤਾ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ । ਇਸ ਵਿਚ ਮੈਡੀਕਲ ਬਾਂਚ, ਸਰਜਰੀ, ਆਰਥੋਪੈਡਿਕ ਅਤੇ ਫਿਜ਼ੀਉਥੇਰੈਪੀ ਸ਼ਾਮਿਲ ਹਨ ।
ਕਿੱਤਾਕਾਰੀ ਪੁਨਰ-ਵਿਸਥਾਪਨ (Vocational Rehabilitation) – ਅਸਮਰਥਤਾ ਦੇ ਬਾਵਜੂਦ, ਅਸਮਰਥਾਂ ਨੂੰ ਆਪਣੀ ਰੋਜ਼ੀ ਕਮਾਉਣ ਲਈ ਕਿੱਤਾਕਾਰੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਮਿਸਾਲ ਦੇ ਤੌਰ ਤੇ ਅੰਨਿਆਂ ਨੂੰ ਕੁਰਸੀ ਬੁਣਨ ਦੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।
ਸਮਾਜਿਕ ਪੁਨਰ-ਵਿਸਥਾਪਨ (Social Rehabilitation) – ਇਸ ਨਾਲ ਅਸਮਰਥ ਦੇ ਪਰਿਵਾਰਕ ਅਤੇ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਬਹਾਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਉਸਦੀ ਅਸਮਰਥਾ ਦੇ ਬਾਵਜੂਦ ਉਸਦੇ ਸਮਾਜਿਕ ਰੁਤਬੇ ਨੂੰ ਹੁਲਾਰਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਮਨੋਵਿਗਿਆਨਿਕ ਪਨਰ-ਵਿਸਥਾਪਨ (Psychological Rehabilitation) – ਇਸ ਵਿਚ ਅਸਮਰਥ ਦਾ ਆਤਮ ਵਿਸ਼ਵਾਸ ਬਹਾਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।ਦਿਮਾਗੀ ਵਿਗਾੜ ਦੇ ਜਾਂ ਦਬਾਉ ਦੀ ਸੂਰਤ ਵਿਚ ਮਨੋਚਕਿਤਸਾ ਵਿਭਾਗ, ਮਨੋਵਿਗਿਆਨਿਕ ਪੁਨਰ-ਵਿਸਥਾਪਨ ਵਿਚ ਮੱਦਦ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਮੁੜ-ਵਸੇਬੇ ਲਈ ਯੋਗਦਾਨ ਦੇਣ ਵਾਲੀਆਂ ਸੰਸਥਾਵਾਂ ਬਾਰੇ ਵਿਸਥਾਰਪੂਰਵਕ ਜਾਣਕਾਰੀ ਦਿਉ ।
ਉੱਤਰ-
ਪੁਨਰ-ਵਿਸਥਾਪਨ ਦਾ ਕਾਰਜ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਹਸਪਤਾਲਾਂ ਵਿੱਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਫਿਰ ਵੀ ਕੁਝ ਵਾਧੂ ਢੰਗਤਰੀਕਿਆਂ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਪੁਨਰ ਵਿਸਥਾਪਨ ਦੀ ਪ੍ਰਕ੍ਰਿਆ ਵਿੱਚ ਕਈ ਪ੍ਰਾਈਵੇਟ ਸਮਾਜਿਕ ਅਦਾਰੇ (ਏਜੰਸੀਆਂ ਕਾਰਜਸ਼ੀਲ ਹਨ । ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੁਝ ਥੈ-ਸੇਵੀ ਸੰਸਥਾਵਾਂ ਹੇਠ ਅਨੁਸਾਰ ਹਨ-

1. ਭਾਰਤੀ ਰੈੱਡ ਕਾਸ ਸੁਸਾਇਟੀ (The Indian Red Cross Society) – ਇਹ ਇੱਕ ਰਾਸ਼ਟਰੀ ਅਦਾਰਾ ਹੈ ਜੋ ਕਿ ਅੰਤਰਰਾਸ਼ਟਰੀ ਰੈੱਡ ਕਾਸ ਸੁਸਾਇਟੀ ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ । ਰੈੱਡ ਕਾਸ ਨੂੰ ਬਿਮਾਰਾਂ ਅਤੇ ਜ਼ਖ਼ਮੀਆਂ ਨੂੰ ਬਚਾਉਣ ਦਾ ਪ੍ਰਤੀਕ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਇੰਟਰਨੈਸ਼ਨਲ ਰੈੱਡ ਕਾਸ ਸੁਸਾਇਟੀ ਸੰਨ 1863 ਵਿੱਚ ਜੇ.ਐੱਸ. ਨੰਤ ਦੁਆਰਾ ਸਥਾਪਿਤ ਕੀਤੀ ਗਈ ਸੀ ਅਤੇ ਇੰਡੀਅਨ ਰੈੱਡ ਖ਼ਾਸ ਸੁਸਾਇਟੀ 1920 ਵਿੱਚ ਹੋਂਦ ਵਿੱਚ ਆਈ । ਇਸ ਦੇ ਭਿੰਨ ਮੰਤਵ ਹਨ- ਸਿਹਤ ਵਿੱਚ ਸੁਧਾਰ, ਬਿਮਾਰੀਆਂ ਤੋਂ ਬਚਾਉ ਅਤੇ ਬਿਮਾਰੀ ਦੀ ਗੰਭੀਰਤਾ ਨੂੰ ਘਟਾਉਣਾ | ਰੈੱਡ ਖ਼ਾਸ ਜੰਗ ਦੇ ਦਿਨਾਂ ਦੌਰਾਨ ਵੀ ਮਦਦ ਕਰਦਾ ਹੈ। ਇਹ ਸ਼ੈ-ਸੇਵੀ ਸੰਸਥਾ, ਭੂਚਾਲ, ਹੜ੍ਹ ਅਤੇ ਤੂਫ਼ਾਨਾਂ ਸਮੇਂ ਜ਼ਖ਼ਮੀ ਹੋਏ ਲੋਕਾਂ ਨੂੰ ਖਾਣ ਵਾਲੀਆਂ ਚੀਜ਼ਾਂ ਅਤੇ ਦਵਾਈਆਂ ਵੀ ਵੰਡਦਾ ਹੈ । ਇੰਡੀਅਨ ਰੈੱਡ ਖ਼ਾਸ ਸੁਸਾਇਟੀ ਦੀਆਂ ਭਾਰਤ ਵਿੱਚ 400 ਤੋਂ ਵੱਧ ਸ਼ਾਖਾਵਾਂ ਹਨ । ਇਹ ਫ਼ੌਜੀਆਂ ਦੀ ਵੀ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ । ਬੰਗਲੌਰ ਵਿੱਚ ਇਸ ਦਾ ਇੱਕ ਬਹੁਤ ਵੱਡਾ ਹਸਪਤਾਲ ਹੈ । ਇੰਡੀਅਨ ਰੈੱਡ ਕਾਸ ਸੁਸਾਇਟੀ ਦੀ ਸੈਂਟ ਜੌਹਨ ਐਂਬੂਲੈਂਸ ਐਸੋਸੀਏਸ਼ਨ ਵੀ ਹੈ ਜਿਸ ਨੇ ਹਜ਼ਾਰਾਂ ਲੋਕਾਂ ਨੂੰ ਫਸਟ ਏਡ ਅਤੇ ਨਰਸਿੰਗ ਦੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਹੈ ।

2. ਸਰਵ-ਭਾਰਤੀ ਅੰਧ ਸਹਾਇਤਾ ਸੰਘ (All India Blind Relief Society) – ਇਹ 1946 ਵਿੱਚ ਸਥਾਪਿਤ ਕੀਤੀ ਗਈ ਸੀ । ਇਹ ਲੋੜਵੰਦਾਂ ਲਈ ਅੱਖਾਂ ਦੇ ਕੈਂਪ ਲਗਾਉਂਦੀ ਹੈ ਅਤੇ ਅੰਨਿਆਂ ਦੀ ਭਲਾਈ ਲਈ ਕਾਰਜਸ਼ੀਲ ਕਈ ਸੰਸਥਾਵਾਂ ਦੇ ਕੰਮ ਦਾ ਤਾਲਮੇਲ ਵੀ ਰੱਖਦੀ ਹੈ ।

3. ਭਾਰਤੀ ਟਿਊਬਰਕਲੌਸਿਸ ਸੰਘ (Tuberculosis Association of India) – ਇਹ ਸੰਸਥਾ 1939 ਵਿੱਚ ਸਥਾਪਿਤ ਹੋਈ ਸੀ । ਇਹ ਤਪਦਿਕ ਨੂੰ ਕੰਟਰੋਲ ਕਰਨ ਅਤੇ ਇਸ ਤੋਂ ਬਚਾਅ ਲਈ ਖੋਜ ਕਾਰਜਾਂ ਵਿੱਚ ਲੱਗੀ ਹੋਈ ਹੈ । ਇਹ ਫੰਡ ਇਕੱਠੇ ਕਰਨ ਲਈ ਹਰ ਸਾਲ ਟੀ.ਬੀ. ਕੰਪੈਨ ਵੀ ਚਲਾਉਂਦੀ ਹੈ । ਟਿਊਬਰਕਲੌਸਿਮ ਐਸੋਸੀਏਸ਼ਨ ਆਫ਼ ਇੰਡੀਆ ਡਾਕਟਰਾਂ ਅਤੇ ਸਮਾਜਿਕ ਕਾਰਕੁਨਾਂ ਲਈ ਸਿਖਲਾਈ ਦਾ ਪ੍ਰਬੰਧ ਵੀ ਕਰਦੀ ਹੈ । ਇਸ ਐਸੋਸੀਏਸ਼ਨ ਦੀਆਂ ਕਈ ਸੰਸਥਾਵਾਂ ਜਿਵੇਂ ਨਿਊ ਦਿੱਲੀ ਟਿਊਬਰਕਲੌਸਿਸ ਸੈਂਟਰ ਅਤੇ ਕਸੌਲੀ ਤੇ ਧਰਮਪੁਰ ਵਿੱਚ ਨਾਟੋਰੀਅਮ (ਅਰੋਗਤਾ ਅਸਥਾਨ ਵੀ ਹਨ ।

4. ਹਿੰਦ ਕੁਸ਼ਟ ਨਿਵਾਰਣ ਸੰਘ (Hind Kusht Nivaran Sangh) – ਇਹ ਨਵੀਂ ਦਿੱਲੀ ਵਿਖੇ 1950 ਵਿੱਚ ਬਣਾਈ ਗਈ ਸੀ । ਇਹ ਸੰਘ ਵਿਸ਼ੇਸ਼ ਤੌਰ ਤੇ ਕੋਹੜੀਆਂ ਲਈ ਕੰਮ ਕਰਦਾ ਹੈ ।ਹਿੰਦ ਕੁਸ਼ਟ ਨਿਵਾਰਣ ਸੰਘ ਦੇਸ਼ ਭਰ ਵਿੱਚ ਕਈ ਕੋਹੜ ਕਲੀਨਿਕਾਂ ਨੂੰ ਮਾਲੀ ਮਦਦ ਵੀ ਦਿੰਦਾ ਹੈ । ਇਸ਼ਤਿਹਾਰਾਂ ਰਾਹੀਂ ਇਹ ਸੰਸਥਾ ਕੋਹੜੀਆਂ ਦੀ ਭਲਾਈ ਲਈ ਲੋਕਾਂ ਨੂੰ ਸਿੱਖਿਅਤ ਕਰਦੀ ਹੈ । ਕੋਹੜ ਇੱਕ ਕੌਨਿਕ ਛੂਤਛਾਤ ਦੀ ਬਿਮਾਰੀ ਹੈ ਜੋ ਕਿ ਚਮੜੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ । ਇਹ ਸੰਸਥਾ ਇੱਕ ਮੈਗਜ਼ੀਨ ਲੈਪਰੋਸੀ ਇੰਨ ਇੰਡੀਆ’ ਵੀ ਪ੍ਰਕਾਸ਼ਿਤ ਕਰਦੀ ਹੈ ।

5. ਭਾਰਤੀ ਬੱਚਾ ਭਲਾਈ ਸੰਘ (Indian Council for Child Welfare) – ਇਹ 1952 ਵਿੱਚ ਬਣਾਈ ਗਈ ਸੀ । ਇਹ ਬੱਚਿਆਂ ਦੀ ਭਲਾਈ ਲਈ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਪ੍ਰੋਗਰਾਮ ਉਲੀਕਦੀ ਹੈ ਅਤੇ ਬੱਚਿਆਂ ਦੀ ਸਿਹਤ ਵਿੱਚ ਸੁਧਾਰ ਲਈ ਸਹਾਇਤਾ ਕਰਦੀ ਹੈ ।

6. ਭਾਰਤੀ ਸੇਵਕ ਸੰਘ (Bharat Sevak Samaj) – ਇਹ 1952 ਵਿੱਚ ਸਥਾਪਿਤ ਹੋਈ ਸੀ । ਇਸ ਸਮਾਜ ਦਾ ਉਦੇਸ਼ ਹੈ, ਚੰਗੀ ਸਿਹਤ ਹਾਸਲ ਕਰਨੀ । ਇਸ ਸਮਾਜ ਦੀ ਮਹੱਤਵਪੂਰਨ ਕਾਰਵਾਈ ਹੈ, ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿੱਚ ਸੈਨੀਟੇਸ਼ਨ (ਸਫ਼ਾਈ ਦਾ ਸੁਧਾਰ ਕਰਨਾ ।

7. ਨੈਸ਼ਨਲ ਸੈਂਟਰ ਫਾਰ ਡੈਫ (National Center for Deaf)-ਇਸ ਏਜੰਸੀ ਦਾ ਸਿਖਲਾਈ ਸੈਂਟਰ ਹੈਦਰਾਬਾਦ ਵਿੱਚ ਹੈ ਜੋ ਕਿ ਬੋਲੇ ਬੱਚਿਆਂ ਦੀ ਬਿਹਤਰੀ ਲਈ ਕੰਮ ਕਰਦਾ ਹੈ ।

8. ਆਲ ਇੰਡੀਆ ਵੋਮੈਨਜ਼ ਕਾਨਫਰੰਸ (All India Women’s Conference) – ਇਸ ਦੀ ਸਥਾਪਨਾ 1926 ਵਿੱਚ ਹੋਈ ਸੀ । ਇਹ ਸੰਸਥਾ ਅਸਮਰਥ ਜਨਾਨੀਆਂ ਅਤੇ ਬੱਚਿਆਂ ਦੀ ਮਦਦ ਕਰਦੀ ਹੈ । ਇਹ ਕਿੱਤਾਕਾਰੀ ਸਿਖਲਾਈ ਲਈ ਵੀ ਕੰਮ ਕਰਦੀ ਹੈ ।

9. ਕਸਤੂਰਬਾ ਗਾਂਧੀ ਯਾਦਯਾਰੀ ਟਰੱਸਟ (Kasturba Gandhi National Memorial Trust) – ਇਹ 1944 ਵਿੱਚ ਬਣਿਆ ਸੀ । ਇਹ ਆਮਤੌਰ ਤੇ ਪਿੰਡਾਂ ਵਿੱਚ ਔਰਤਾਂ ਦੀ ਭਲਾਈ ਦੀ ਦੇਖਭਾਲ ਕਰਦਾ ਹੈ । ਇਹ ਕੋਹੜ ਵਿਰੋਧੀ ਕੰਮਾਂ ਵਿੱਚ ਵੀ ਕਾਰਜਸ਼ੀਲ ਹੈ ।

10. ਅੰਨਿਆਂ ਲਈ ਉਦਯੋਗਿਕ ਘਰ (Industrial Home for Blind) -1971 ਵਿੱਚ ਬਣਾਈ ਗਈ ਇਹ ਸੰਸਥਾ ਮੁੰਬਈ ਵਿਚ ਸਥਿਤ ਹੈ ਅਤੇ ਇੱਥੇ ਅੰਨ੍ਹੇ ਬੱਚਿਆਂ ਨੂੰ ਕਿੱਤਾ ਅਗਵਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ਤਾਂ ਜੋ ਉਹ ਅਸਮਰਥ ਹੋਣ ਦੇ ਬਾਵਜੂਦ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਖ਼ੁਦ ਕਰ ਸਕਣ ।

11. ਆਸ਼ਾ ਨਿਕੇਤਨ ਰੀਹੈਬਲੀਟੇਸ਼ਨ ਸੈਂਟਰ (Asha Niketan Rehabilitation Center) – ਇਹ 1960 ਵਿੱਚ ਬਣੀ ਸੀ । ਇਸ ਦਾ ਇੱਕ ਹਸਪਤਾਲ ਹੈ ਜਿਸ ਵਿੱਚ ਫੀਜ਼ੀਉਥਰੈਪਿਕ ਯੂਨਿਟ ਹੈ । ਇਸ ਦੇ ਅਧੀਨ ਇੱਕ ਦਿਮਾਗੀ ਤੌਰ ‘ਤੇ ਕਮਜ਼ੋਰ ਬੱਚਿਆਂ ਅਤੇ ਬੋਲਿਆਂ ਲਈ ਸਕੂਲ ਵੀ ਹੈ ।

12. ਬਣਾਉਟੀ ਅੰਗ ਤਿਆਰ ਕਰਨ ਵਾਲੀ ਸੰਸਥਾ (Artificial Limbs Manufacturing Corporation) – ਇਹ ਕਾਰਪੋਰੇਸ਼ਨ ਕਾਨਪੁਰ ਵਿਖੇ ਬਣਾਈ ਗਈ ਸੀ । ਇੱਥੇ ਅਸਮਰਥਾ ਲਈ ਬਨਾਵਟੀ ਅੰਗਾਂ ਦਾ ਉਤਪਾਦਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

13. ਮੰਦਬੁੱਧੀ ਬੱਚਿਆਂ ਲਈ ਕਮਯਾਨੀ ਸਕੂਲ (Kamayani School for Mentally Handicapped) – ਇਹ . ਸਕੂਲ ਪੂਨਾ ਵਿਖੇ 1964 ਵਿੱਚ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਸੀ । ਇਸ ਸਕੂਲ ਵਿੱਚ ਅਸਮਰਥ, ਖ਼ਾਸ ਤੌਰ ‘ਤੇ ਦਿਮਾਗੀ’ ਤੌਰ ‘ਤੇ ਕਮਜ਼ੋਰਾਂ ਨੂੰ ਕਿੱਤਾ ਸਿਖਲਾਈ ਜਿਵੇਂ ਫਰਨੀਚਰ ਨੂੰ ਪਾਲਿਸ਼ ਕਰਨੀ ਆਦਿ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।

ਇਨ੍ਹਾਂ ਸੰਸਥਾਵਾਂ ਤੋਂ ਇਲਾਵਾ ਹੋਰ ਕਈ ਸਮਾਜ ਸੇਵੀ ਅਦਾਰੇ ਪੁਨਰਵਿਸਥਾਪਨ ਦਾ ਕੰਮ ਕਰ ਰਹੇ ਹਨ । ਉਦਾਹਰਨ ਵਜੋਂ ਇੰਡੀਅਨ ਕੌਂਸਲ ਆਫ਼ ਮੈਂਟਲ ਹਾਈਜੀਨ, ਇੰਡੀਅਨ ਕਾਨਫਰੰਸ ਆਫ਼ ਸੋਸ਼ਲ ਵਰਕ, ਰਾਮਾ ਕ੍ਰਿਸ਼ਨ ਮਿਸ਼ਨ, ਲਾਇਨਜ਼ ਕਲੱਬ, ਮਾਰਵਾੜੀ ਰਿਲੀਫ ਸੋਸਾਇਟੀ, ਆਈ. ਆਈ. ਟੀ. ਦਿੱਲੀ ਨੈਸ਼ਨਲ ਫਿਜ਼ੀਕਲ ਲੈਬਾਰਟਰੀ, ਨਵੇਦਿਕ ਪ੍ਰੋਸਥੈਟਿਕ ਸੈਂਟਰ ਚੰਡੀਗੜ੍ਹ ਆਦਿ ।

ਪੁਨਰਵਿਸਥਾਪਨ ਵਿੱਚ ਸਮਾਜ ਦੀ ਭੂਮਿਕਾ (Role of Community in Rehabilitation) – ਪੁਨਰਵਿਸਥਾਪਨ ਦੇ ਕੰਮ ਵਿੱਚ ਸਮਾਜ ਦੀ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਹੈ । ਸਮਾਜ ਦੇ ਹਰ ਮੈਂਬਰ ਨੂੰ ਅਪਾਹਜ ਦੀ ਮਦਦ ਹਮਦਰਦੀ ਅਤੇ ਸਨੇਹ ਨਾਲ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਜੇ ਸਮਾਜ ਅਸਮਰਥ ਨੂੰ ਅਲੱਗ ਕਰ ਦੇਵੇ ਤਾਂ ਉਸਦੀ ਹਾਲਤ ਹੋਰ ਵੀ ਮਾੜੀ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਸ ਲਈ ਸਮਾਜ ਨੂੰ ਅਪਾਹਜ ਦੀ ਸਹਾਇਤਾ ਤਰਸ ਵਜੋਂ ਨਹੀਂ ਸਗੋਂ ਇੱਕ ਸਦਾਚਾਰਕ ਫਰਜ਼ ਵਜੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਅਸਮਰਥ ਨੂੰ ਹੌਂਸਲਾ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ ।

PSEB 12th Class Physical Education Guide ਅਸਮਰਥਾ Important Questions and Answers

ਇੱਕ ਅੰਕ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (One Mark Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਮੁੜ-ਵਸੇਬੇ ਦਾ ਅਰਥ ਸਮਝਾਓ ।
ਉੱਤਰ-
ਸ਼ਬਦ ‘‘ਰੀਹੈਬਲੀਟੇਸ਼ਨ’’ ਸ਼ਬਦ ਹੈਬੀਲਿਟਾਂ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ ਜਿਸਦਾ ਅਰਥ ਹੈ ਸਮਰੱਥਾ । ਇਸ ਲਈ ਪੁਨਰ ਵਿਸਥਾਪਨ ਦਾ ਅਰਥ ਹੈ ‘ਮੁੜ ਕਬਜ਼ਾ’’ । ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿਚ ਪੁਨਰਵਿਸਥਾਪਨ ਦਾ ਅਰਥ ਹੈ ‘‘ਪਹਿਲੀ ਤੰਦਰੁਸਤੀ ਪ੍ਰਾਪਤ ਕਰਨਾ ਜਾਂ ਰਾਜ਼ੀ ਹੋਣਾ ਅਤੇ ਟਿਕ ਜਾਣਾ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਵੀ ਦੋ ਤਰ੍ਹਾਂ ਦੀ ਅਸਮਰਥਾ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-

ਬਣਤਰ ਅਪੰਗਤਾ
ਕਾਰਜਾਤਮਿਕ ਅਪੰਗਤਾ ।

ਪ੍ਰਸ਼ਨ 3.
WHO ਦਾ ਪੂਰਾ ਨਾਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵਰਲਡ ਹੈਲਥ ਆਰਗਨਾਈਜੇਸ਼ਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਕਿਸੇ ਵੀ ਦੋ ਢਾਂਚਾਗਤ ਅਪਾਹਜਤਾ ਦਾ ਨਾਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਕਾਈਫੋਸਿਸ ਅਤੇ ਲੋਰਡੋਸਿਸ ।

ਪ੍ਰਸ਼ਨ 5.
ਅਸਮਰਥਾ ਦੇ ਕੋਈ ਦੋ ਕਾਰਕਾਂ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ।
ਉੱਤਰ-

ਮਾਨਸਿਕ ਕਾਰਨ
ਸਰੀਰਕ ਕਾਰਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਕਿਸੇ ਵੀ ਦੋ ਰਸਾਇਣਾਂ ਦੇ ਨਾਮ ਲਿਖੋ ਜਿਸ ਤੋਂ ਅਸਮਰਥਾ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-

ਕਾਰਬਨ ਮੋਨੋਆਕਸਾਈਡ
ਸਲਫਰ ਡਾਈਆਕਸਾਈਡ ।

ਪ੍ਰਸ਼ਨ 7.
ਕੋਈ ਵੀ ਦੋ ਭੌਤਿਕ ਏਜੰਟਾਂ ਦੇ ਨਾਮ ਦੱਸੋ ਜਿਸ ਨਾਲ ਕਿੱਤਾ ਬਿਮਾਰੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ।
ਉੱਤਰ-
ਬਹੁਤ ਗਰਮ ਤਾਪਮਾਨ ਅਤੇ ਬਹੁਤ ਠੰਡਾ ਤਾਪਮਾਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਆਮ ਕਿੱਤਾ ਸੰਬੰਧੀ ਬਿਮਾਰੀਆਂ ਵਿਚ ਧੂੜ ਦੇ ਖਤਰੇ ਨੂੰ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ-
ਕੋਲੇ, ਸਿਲਿਕਾ ਧੂੜ ਅਤੇ ਕਪਾਹ ਦੀ ਧੂੜ ਤੋਂ ਭੁਰਾ ਫੇਫੜਾ ਨਾਲ ਬਿਮਾਰੀ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਅਸਮਰਥਾ ਦੀ ਰੋਕਥਾਮ ਲਈ ਕੋਈ ਦੋ ਉਪਚਾਰ ਲਿਖੋ ।
ਉੱਤਰ-
ਮੈਡੀਕਲ ਚੈਕਅਪ ਅਤੇ ਕੰਮ ਦੇ ਸਥਾਨ ਦਾ ਰੱਖਰਖਾਵ ।

ਪ੍ਰਸ਼ਨ 10.
ਵਾਤਾਵਰਣ ਪ੍ਰਦੂਸ਼ਣ ਦੇ ਦੋ ਕਾਰਨ ਲਿਖੋ ।
ਉੱਤਰ-
ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਅਤੇ ਰੌਲਾ ਪ੍ਰਦੁਸ਼ਣ ।

ਪ੍ਰਸ਼ਨ 11.
ਮੁੜ-ਵਸੇਬੇ ਵਿਚ ‘‘ਹੇਬੀਟਾ’’ (Habita) ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਸਮਰੱਥਾ ।

ਪ੍ਰਸ਼ਨ 12.
ਮੁੜ-ਵਸੇਬੇ ਕਿਸ ਭਾਸ਼ਾ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ ?
ਉੱਤਰ-
ਯੂਨਾਨੀ ਭਾਸ਼ਾ ਤੋਂ ।

ਪ੍ਰਸ਼ਨ 13.
ਮੁੜ-ਵਸੇਬੇ ਦੇ ਕੋਈ ਦੋ ਖੇਤਰਾਂ ਦਾ ਨਾਮ ਲਿਖੋ ।
ਉੱਤਰ-
ਡਾਕਟਰੀ ਪੁਨਰ ਵਿਸਥਾਪਣ ਅਤੇ ਕਿੱਤਾਕਾਰੀ ਪੁਨਰ ਵਿਸਥਾਪਣ ।

ਪ੍ਰਸ਼ਨ 14.
ਮੁੜ-ਵਸੇਬੇ ਦੇ ਕੰਮ ਵਿਚ ਲੱਗੀਆਂ ਕਿਸੇ ਦੋ ਸੰਸਥਾਵਾਂ ਦਾ ਨਾਮ ਲਿਖੋ ।
ਉੱਤਰ-

ਇੰਡੀਅਨ ਰੈੱਡ ਕਰਾਸ ਸੁਸਾਇਟੀ
ਆਲ ਇੰਡੀਆ ਬਲਾਈਂਡ ਰਿਲੀਫ਼ ਸੁਸਾਇਟੀ ।

ਪ੍ਰਸ਼ਨ 15.
ਭਾਰਤੀ ਰੈੱਡ ਕਰਾਸ ਸੁਸਾਇਟੀ ਕਦੋਂ ਹੋਂਦ ਵਿਚ ਆਈ ਸੀ ?
ਉੱਤਰ-
1920 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 16.
ਕਿਸ ਸਾਲ ਵਿਚ ਕਮਯਾਨੀ ਸਕੂਲ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ਗਈ ਸੀ ?
ਉੱਤਰ-
1964 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 17.
ਨਕਲੀ ਅੰਗਾਂ ਨੂੰ ਬਣਾਉਣ ਲਈ ਕਾਰਪੋਰੇਸ਼ਨ ਨੂੰ ਕਿੱਥੇ ਬਣਾਇਆ ਗਿਆ ਹੈ ।
ਉੱਤਰ-
ਕਾਨਪੁਰ ।

ਪ੍ਰਸ਼ਨ 18.
ਕਿਹੜੀ ਸੰਸਥਾ ਬੋਲਿਆਂ ਲਈ ਕੰਮ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਨੈਸ਼ਨਲ ਸੈਂਟਰ ਆਫ ਡੈਫ਼ ।

ਪ੍ਰਸ਼ਨ 19.
ਕਿਹੜੀ ਸੰਸਥਾ ਜੋ ਬੱਚਿਆਂ ਦੇ ਵੈਲਫੇਅਰ ਲਈ ਕੰਮ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤੀ ਬੱਚਾ ਭਲਾਈ ਸੰਘ ।

ਪ੍ਰਸ਼ਨ 20.
ਕਿਹੜੇ ਸਾਲ ਵਿਚ ਭਾਰਤ ਵਿਚ ਟੂਬਰਕਲੋਸਿਸ ਐਸੋਸੀਏਸ਼ਨ ਨੂੰ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
1939 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 21.
ਕਮਯਾਨੀ ਸਕੂਲ ਕਿਸ ਸ਼ਹਿਰ ਵਿਚ ਸਥਿਤ ਹੈ ?
ਉੱਤਰ-
ਪੂਨਾ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 22.
ਭਾਈਫੋਸਿਸ ਵਿਚ ਸਰੀਰ ਦੇ ਕਿਸ ਭਾਗ ‘ਤੇ ਅਸਰ ਪੈਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਰੀੜ ਦੀ ਹੱਡੀ ਦੇ ਪਿੱਠ ਵਾਲੇ ਪਾਸੇ ।

ਪ੍ਰਸ਼ਨ 23.
ਲੋਰਡੋਸਿਸ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਲੱਕ ਪਾਸੇ ਆਏ ਵਾਧੇ ਦੀ ਅਪੰਗਤਾ ਹੈ । ਇਸ ਵਿਚ ਸਰੀਰ ਦੇ ਉੱਪਰਲੇ ਭਾਗ ਵਿਚ ਝੁਕਾਅ ਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 24.
ਸਕੌਲਸਿਸ ਅਪੰਗਤਾ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਇਸ ਅਪੰਗਤਾ ਵਿਚ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਇਕ ਪਾਸੇ ਨੂੰ ਟੇਢੀ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 25.
ਪੁਨਰ-ਵਸੇਬੇ ਕੌਂਸਲ ਦੇ ਅਨੁਸਾਰ ਅਪੰਗਤਾ ਨੂੰ ਕਿੰਨੇ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ?
ਉੱਤਰ-
ਚਾਰ ਭਾਗਾਂ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 26.
ਸਰਵ-ਭਾਰਤੀ ਅੰਧ ਸਹਾਇਤਾ ਸੰਘ ਕਿਸ ਸਾਲ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
ਸਾਲ 1946 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 27.
ਹਿੰਦ ਕੁਸ਼ਟ ਨਿਵਾਰਣ ਸੰਘ ਕਿਸ ਸਾਲ ਆਰੰਭ ਹੋਇਆ ਅਤੇ ਕਿੱਥੇ ਹੈ ?
ਉੱਤਰ-
ਸਾਲ 1950 ਵਿਚ, ਨਵੀਂ ਦਿੱਲੀ ਵਿਖੇ ।

ਪ੍ਰਸ਼ਨ 28.
ਭਾਰਤ ਸੇਵਕ ਸੰਘ ਦੀ ਸਥਾਪਨਾ ਕਦੋਂ ਹੋਈ ਸੀ ?
ਉੱਤਰ-
ਸਾਲ 1952 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 29.
ਨੈਸ਼ਨਲ ਸੈਂਟਰ ਫਾਰ ਡੈਫ ਕਿੱਥੇ ਸਥਿਤ ਹੈ ?
ਉੱਤਰ-
ਹੈਦਰਾਬਾਦ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 30.
ਅੰਨਿਆਂ ਦੇ ਉਦਯੋਗਿਕ ਘਰ ਕਿੱਥੇ ਹਨ ?
ਉੱਤਰ-
ਮੁੰਬਈ ਵਿਚ ।

ਦੋ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Two Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਅਸਮਰਥਾ ਤੋਂ ਤੁਹਾਡਾ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਅਸਮਰਥਾ ਦਾ ਅਰਥ ਹੈ, ਕੋਈ ਵਿਸ਼ੇਸ਼ ਸਰੀਰਕ ਜਾਂ ਮਾਨਸਿਕ ਕੰਮ ਕਰਨ ਦੀ ਅਸਮਰਥਾ । ਜਦੋਂ ਸਰੀਰਕ ਮਾਨਸਿਕ ਕਾਰਜ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਘੱਟ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇਸ ਅਵਸਥਾ ਨੂੰ ਅਸਮਰਥਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਅਸਮਰਥਾ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਕਿਸਮਾਂ ਨੂੰ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ-
ਅਸਮਰਥਾ ਦੀਆਂ ਕਿਸਮਾਂ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-
1. ਬਣਤਰ ਅਸਮਰਥਾ (Structural Disability) – ਇਹ ਅਸਮਰਥਾ ਸਰੀਰਕ ਬਣਤਰ ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ । ਇਸ ਵਿਚ ਸਰੀਰ ਦਾ ਬੇਢੰਗਾ ਅਤੇ ਕਰੂਪਤਾ ਆਉਂਦੇ ਹਨ । ਸਰੀਰ ਦੀ ਇਹ ਹਾਲਤ ਕਿਸੇ ਵੀ ਐਕਸੀਡੈਂਟ ਜਾਂ ਸੱਟ ਨਾਲ ਹੋ ਸਕਦੀ ਹੈ । ਇਸ ਦੇ ਕਈ ਕਾਰਨ ਹੋ ਸਕਦੇ ਹਨ ਜਿਵੇਂ, ਦੁਰਘਟਨਾਵਾਂ, ਅਸੰਤੁਲਿਤ ਖੁਰਾਕ ਅਤੇ ਕੰਮ ਕਰਦੇ ਸਮੇਂ ਕੀਤੀਆਂ ਗਲਤੀਆਂ |

2. ਕਾਰਜਾਤਮਿਕ ਅਸਮਰਥਤਾ (Functional Disability) – ਇਸ ਕਿਸਮ ਦੀ ਅਸਮਰਥਤਾ ਵਿਚ ਸਰੀਰਕ ਅੰਗ ਪ੍ਰਭਾਵਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਹ ਨੁਕਸ ਆਮ ਕਰਕੇ ਲੰਬੀ ਬਿਮਾਰੀਆਂ ਕਾਰਨ ਹੁੰਦੇ ਹਨ । ਸਾਹ ਦੀ ਬਿਮਾਰੀ, ਸਿੱਲੀਕੋਸਿਸ, ਐਸਬੈਗਸ, ਲੀਡ ਕਹਿਰ, ਸਾਈਡਰੋਸਿਸ, ਬਾਈਸਨੋਸਿਸ, ਲੇਬਰੋਸਿਸ, ਲੰਗ ਕੈਂਸਰ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਕਾਰਜਸ਼ੀਲ ਅਸਮਰਥਾ ਸ਼ਬਦ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਇਸ ਕਿਸਮ ਦੀ ਅਸਮਰਥਾ ਵਿਚ ਸਰੀਰਕ ਅੰਗ ਪ੍ਰਭਾਵਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਹ ਨੁਕਸ ਆਮ ਕਰਕੇ ਲੰਬੀ ਬਿਮਾਰੀਆਂ ਕਾਰਨ ਹੁੰਦੇ ਹਨ । ਸਾਹ ਦੀ ਬਿਮਾਰੀ, ਸਿੱਲੀਕੋਸਿਸ, ਐਸਬੈਗਸ, ਲੀਡ ਕਹਿਰ, ਸਾਈਡਰੋਸਿਸ, ਬਾਈਸਨੋਸਿਸ, ਲੇਬਰੋਸਿਸ, ਲੰਗ ਕੈਂਸਰ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਮੁੜ-ਵਸੇਬੇ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਡਬਲਯੂ. ਐੱਚ. ਓ. (W.H.O.) ਦੇ ਅਨੁਸਾਰ, “ਪੁਨਰ ਵਿਸਥਾਪਨ, ਜਾਂ ਮੁੜ ਵਸੇਰਾ ਅਪੰਗ ਵਿਅਕਤੀ ਵਿਚ ਕੰਮ ਕਰਨ ਦੀ ਉਚਤਮ ਯੋਗਤਾ ਪੈਦਾ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਹਿੱਤ ਉਸਦੀ ਪੁਨਰ ਸਿਖਲਾਈ ਲਈ ਡਾਕਟਰੀ, ਸਮਾਜਿਕ, ਵਿੱਦਿਅਕ ਅਤੇ ਕਿੱਤਾਕਾਰੀ ਢੰਗਾਂ ਦੀ ਸਮੁੱਚੀ ਅਤੇ ਸੰਯੁਕਤ ਵਰਤੋਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਪੁਨਰਵਾਸ ਦੇ ਸ਼ਬਦਾਵਲੀ ਅਰਥ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
‘‘ਰੀਹੈਬਲੀਟੇਸ਼ਨ’’ ਸ਼ਬਦ ਹੈਬੀਲਿਟਾਂ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ ਜਿਸਦਾ ਅਰਥ ਹੈ ਸਮਰੱਥਾ । ਇਸ ਲਈ ਪੁਨਰ ਵਿਸਥਾਪਨ ਦਾ ਅਰਥ ਹੈ ‘‘ਮੁੜ ਵਸੇਬਾ (ਪੁਨਰਵਾਸ) ” । ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿਚ ਪੁਨਰਵਿਸਥਾਪਨ ਦਾ ਅਰਥ ਹੈ ‘‘ਪਹਿਲੀ ਤੰਦਰੁਸਤੀ ਪ੍ਰਾਪਤ ਕਰਨਾ ਜਾਂ ਰਾਜ਼ੀ ਹੋਣਾ ਅਤੇ ਟਿਕ ਜਾਣਾ ।

ਪ੍ਰਸ਼ਨ 6.
ਵੱਖ-ਵੱਖ ਏਜੰਟਾਂ ਦੀ ਸੂਚੀ ਬਣਾਓ ਜਿਸ ਕਾਰਨ ਆਮ ਕਿੱਤਾ ਬਿਮਾਰੀਆਂ ਹੋਣ ।
ਉੱਤਰ-

ਭੌਤਿਕ ਕਾਰਨਾਂ ਕਰਕੇ ਪੈਦਾ ਹੋਏ ਰੋਗ (Diseases due to Physical agents)
ਧੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Dust Diseases or Dust hazard)
ਰਸਾਇਣਿਕ ਤੱਤਾਂ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Chemical diseases or chemical hazards)
ਅਸਧਾਰਨ ਸਮੇਂ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਪੈਦਾ ਹੋਏ ਰੋਗ ।

ਪ੍ਰਸ਼ਨ 7.
ਮੁੜ-ਵਸੇਬੇ ਦੇ ਦੋ ਖੇਤਰਾਂ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ

ਡਾਕਟਰੀ ਮੁੜ-ਵਸੇਬਾ (Medical Rehabilitation) – ਕਿਸੇ ਸੱਟ ਜਾਂ ਬਿਮਾਰੀ ਨਾਲ ਆਏ ਕਿਸੇ ਸਰੀਰਕ ਵਿਗਾੜ ਦੀ ਸੂਰਤ ਵਿਚ ਮਾਹਿਰ ਡਾਕਟਰੀ ਸਹਾਇਤਾ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ । ਇਸ ਵਿਚ ਮੈਡੀਕਲ ਬ੍ਰਾਂਚ, ਸਰਜਰੀ, ਆਰਥੋਪੈਡਿਕ ਅਤੇ ਫਿਜ਼ੀਓਥਰੈਪੀ ਸ਼ਾਮਿਲ ਹਨ ।
ਕਿੱਤਾਕਾਰੀ ਮੁੜ ਵਸੇਬਾ (Vocational Rehabilitation) – ਅਪਾਹਜਤਾ ਦੇ ਬਾਵਜੂਦ, ਅਪਾਹਜਾਂ ਨੂੰ ਆਪਣੀ ਰੋਜ਼ੀ ਕਮਾਉਣ ਲਈ ਕਿੱਤਾਕਾਰੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਮਿਸਾਲ ਦੇ ਤੌਰ ਤੇ ਅੰਨ੍ਹਿਆਂ ਨੂੰ ਕੁਰਸੀ ਬੁਣਨ ਦੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਪੁਨਰਵਾਸ ਲਈ ਸੇਵਾਵਾਂ ਪ੍ਰਦਾਨ ਕਰਨ ਵਾਲੀਆਂ ਵੱਖ-ਵੱਖ ਸੰਸਥਾਵਾਂ ਦੇ ਨਾਮ ਲਿਖੋ ।
ਉੱਤਰ-

ਇੰਡੀਅਨ ਰੈੱਡ ਕਰਾਸ ਸੁਸਾਇਟੀ
ਆਲ ਇੰਡੀਆ ਬਲਾਈਂਡ ਰਿਲੀਫ ਸੁਸਾਇਟੀ
ਟਿਊਬਰਕਲੋਸਿਸ ਐਸੋਸੀਏਸ਼ਨ ਆਫ਼ ਇੰਡੀਆ ।

ਪ੍ਰਸ਼ਨ 9.
ਅਪਾਜਤਾ ਲਈ ਵੱਖ-ਵੱਖ ਰੋਕਥਾਮ ਦੇ ਦੋ ਉਪਾਵਾਂ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ।
ਉੱਤਰ-

ਨੌਕਰੀ ਤੇ ਰੱਖਣ ਤੋਂ ਪਹਿਲਾਂ ਮੈਡੀਕਲ ਚੈੱਕਅਪ
ਕਰਮਚਾਰੀਆਂ ਦੀ ਸਮੇਂ-ਸਮੇਂ ਤੇ ਜਾਂਚ ਹੋਣਾ ।

ਪ੍ਰਸ਼ਨ 10.
ਕਿਸੇ ਵੀ ਦੋ ਆਮ ਪੇਸ਼ਾਵਰ ਬਿਮਾਰੀਆਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
1. ਕਪਾਹ ਦੀ ਧੂੜ/ਬਿਸੀਨੋਸਿਸ (Cotton dust/Byssinosis) – ਇਸਨੂੰ ਭੂਰਾ ਫੇਫੜਾ (Brown lung) ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਹ ਉਦੋਂ ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਕਰਮਚਾਰੀ ਭੰਗ, ਗਣ ਅਤੇ ਕਪਾਹ ਦੀ ਸੋਸਿੰਗ ਦੇ ਕੰਮ ਦੇ ਦੁਆਰਾ ਧੂੜ ਨੂੰ ਸਾਹ ਦੁਆਰਾ ਸਰੀਰ ਦੇ ਅੰਦਰ ਲੈਂਦਾ ਹੈ । ਇਹ ਇਕ ਭਿਅੰਕਰ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਛਾਤੀ ਤੰਗ ਜਾਂ ਜਕੜ ਜਾਂਦੀ ਹੈ ਅਤੇ ਸਾਹ ਦੀ ਕਮੀ ਹੋਣ ਲੱਗਦੀ ਹੈ । ਇਹ ਮੁੱਖ ਕਰਕੇ ਟੈਕਸਟਾਈਲ ਦੀਆਂ ਫੈਕਟਰੀਆਂ ਵਿਚ ਕੱਪੜਿਆਂ ਦਾ ਕੰਮ-ਕਾਜ ਕਰਦੇ ਹਨ ।

2. ਕਿੱਤਾ ਅਸਥਮਾ (Occupation Asthma) – ਇਹ ਦਮਾਂ ਧੂੜ, ਗੈਸਾਂ, ਧੂੰਆਂ ਅਤੇ ਵਾਸ਼ਪ ਆਦਿ ਵਿਚ ਸਾਹ ਲੈਣ ਕਾਰਨ ਹੁੰਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਦਮੇ ਦੇ ਲੱਛਣ ਭਿਅੰਕਰ ਖੰਘ ਅਤੇ ਘਬਰਾਹਟ ਹਨ ।

ਪ੍ਰਸ਼ਨ 11.
ਬਾਲ ਕਲਿਆਣ ਭਾਰਤ ਕੌਂਸਲ ਦਾ ਕੀ ਕੰਮ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਕੌਂਸਲ 1952 ਵਿੱਚ ਬਣਾਈ ਗਈ ਸੀ । ਇਹ ਬੱਚਿਆਂ ਦੀ ਭਲਾਈ ਲਈ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਪ੍ਰੋਗਰਾਮ ਉਲੀਕਦੀ ਹੈ ਅਤੇ ਬੱਚਿਆਂ ਦੀ ਸਿਹਤ ਵਿੱਚ ਸੁਧਾਰ ਲਈ ਸਹਾਇਤਾ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਕਾਮਯਨੀ ਸਕੂਲ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ-
ਇਹ ਸਕੂਲ ਪੂਨਾ ਵਿਖੇ 1964 ਵਿੱਚ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਸੀ । ਇਸ ਸਕੂਲ ਵਿੱਚ ਅਪਾਹਜ, ਖ਼ਾਸ ਤੌਰ ‘ਤੇ ਦਿਮਾਗੀ ਤੌਰ ‘ਤੇ ਕਮਜ਼ੋਰਾਂ ਨੂੰ ਕਿੱਤਾ ਸਿਖਲਾਈ , ਜਿਵੇਂ ਫਰਨੀਚਰ ਨੂੰ ਪਾਲਿਸ਼ ਕਰਨੀ ਆਦਿ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਆਸ਼ਾ ਨਿਕੇਤਨ ਮੁੜ-ਵਸੇਬਾ ਕੇਂਦਰ ਬਾਰੇ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਇਹ 1960 ਵਿੱਚ ਬਣੀ ਸੀ । ਇਸ ਦਾ ਇੱਕ ਹਸਪਤਾਲ ਹੈ ਜਿਸ ਵਿੱਚ ਫੀਜ਼ੀਓਥਰੈਪਿਕ ਯੂਨਿਟ ਹੈ । ਇਸ ਦੇ ਅਧੀਨ ਇੱਕ ਦਿਮਾਗੀ ਤੌਰ ‘ਤੇ ਕਮਜ਼ੋਰ ਬੱਚਿਆਂ ਅਤੇ ਬੋਲਿਆਂ ਲਈ ਸਕੂਲ ਵੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
ਆਲ ਇੰਡੀਆ ਬਲਾਈਂਡ ਰਿਲੀਫ ਸੁਸਾਇਟੀ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ-
ਇਹ 1946 ਵਿੱਚ ਸਥਾਪਿਤ ਕੀਤੀ ਗਈ ਸੀ । ਇਹ ਲੋੜਵੰਦਾਂ ਲਈ ਅੱਖਾਂ ਦੇ ਕੈਂਪ ਲਗਾਉਂਦੀ ਹੈ ਅਤੇ ਅੰਨਿਆਂ ਦੀ ਭਲਾਈ ਲਈ ਕਾਰਜਸ਼ੀਲ ਕਈ ਸੰਸਥਾਵਾਂ ਦੇ ਕੰਮ ਦਾ ਤਾਲਮੇਲ ਵੀ ਰੱਖਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਲੋਰਡੋਸਿਸ ਅਪੰਗਤਾ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ-
ਇਹ ਅਪੰਗਤਾ, ਲੱਕ ਵਾਲੇ ਪਾਸੇ ਆਏ ਵਾਧੇ ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਸਰੀਰ ਦੇ ਉੱਪਰਲੇ ਭਾਗ ਵਿਚ ਅੱਗੇ ਵੱਲ ਝੁਕਾਅ ਆ ਜਾਂਦਾ ਹੈ ।

ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Three Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਅਸਮਰਥਾ ਦੀਆਂ ਕਿਸਮਾਂ ਨੂੰ ਵਿਸਤ੍ਰਿਤ ਕਰੋ ।
ਉੱਤਰ-
1. ਬਣਤਰ ਅਸਮਰਥਾ (Structural Disability) – ਇਹ ਅਪੰਗਤਾ ਸਰੀਰਕ ਬਣਤਰ ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ । ਇਸ ਵਿਚ ਸਰੀਰ ਦਾ ਬੇਢੰਗਾ ਅਤੇ ਕਰੂਪਤਾ ਆਉਂਦੇ ਹਨ । ਸਰੀਰ ਦੀ ਇਹ ਹਾਲਤ ਕਿਸੇ ਵੀ ਐਕਸੀਡੈਂਟ ਜਾਂ ਸੱਟ ਨਾਲ ਹੋ ਸਕਦੀ ਹੈ । ਇਸ ਦੇ ਕਈ ਕਾਰਨ ਹੋ ਸਕਦੇ ਹਨ ਜਿਵੇਂ, ਦੁਰਘਟਨਾਵਾਂ, ਅਸੰਤੁਲਿਤ ਖੁਰਾਕ ਅਤੇ ਕੰਮ ਕਰਦੇ ਸਮੇਂ ਕੀਤੀਆਂ ਗਲਤੀਆਂ । ਸਰੀਰਕ ਬਣਤਰ ਦੇ ਅਨੁਸਾਰ ਹੇਠ ਲਿਖੀਆਂ ਅਪੰਗਤਾਵਾਂ ਆਉਂਦੀਆਂ ਹਨ-

(ੳ) ਕਾਈਕੋਸਿਸ (Kyphosis) – ਇਹ ਅਪੰਗਤਾ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਦੇ ਪਿੱਠ ਵਾਲੇ ਪਾਸੇ ਡਰੋਸਲ ਵਿਚ ਹੋਏ ਵਾਧੇ | ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਪਿੱਠ ਵਿਚ ਕੁੱਬ ਪੈ ਜਾਂਦਾ ਹੈ ।
(ਅ) ਲੋਰਡੋਸਿਸ (Lordosis) – ਇਹ ਅਪੰਗਤਾ, ਲੱਕ ਵਾਲੇ ਪਾਸੇ ਆਏ ਵਾਧੇ ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਸਰੀਰ । ਦੇ ਉੱਪਰਲੇ ਭਾਗ ਵਿਚ ਅੱਗੇ ਵੱਲ ਝੁਕਾਅ ਆ ਜਾਂਦਾ ਹੈ ।
(ਇ) ਸਕੌਲਸਿਸ (Scoliosis) – ਇਹ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਦੇ ਲਟੇਰਲ ਵਿਚ ਆਏ ਵਾਧੇ ਨਾਲ ਹੁੰਦਾ ਹੈ ।

2. ਕਾਰਜਾਤਮਿਕ ਅਸਮਰਥਾ (Functional Disability) – ਇਸ ਕਿਸਮ ਦੀ ਅਸਮਰਥਾ ਵਿਚ ਸਰੀਰਕ ਅੰਗ ਪ੍ਰਭਾਵਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਹ ਨੁਕਸ ਆਮ ਕਰਕੇ ਲੰਬੀ ਬਿਮਾਰੀਆਂ ਕਾਰਨ ਹੁੰਦੇ ਹਨ | ਸਾਹ ਦੀ ਬਿਮਾਰੀ, ਸਿੱਲੀਕੋਸਿਸ, ਐਸਬੈਗਟਸ, ਲੀਡ ਕਹਿਰ, ਸਾਈਡਰੋਸਿਸ, ਬਾਈਸਨੋਸਿਸ, ਲੇਬਰੋਸਿਸ, ਲੰਗ ਕੈਂਸਰ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਅਸਮਰਥਾ ਵਾਲੇ ਦੋ ਕਾਰਕਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
1. ਭੌਤਿਕ ਕਾਰਨ (Physical Factor) – ਬਹੁਤ ਸਾਰੀਆਂ ਅਯੋਗਤਾਵਾਂ ਭੌਤਿਕ ਕਾਰਨਾਂ ਜਿਵੇਂ ਕਿ ਗਰਮੀ, ਸਰਦੀ, ਰੋਸ਼ਨੀ, ਦਬਾਅ, ਰੌਲਾ, ਵਿਕੀਰਣਾਂ (Radiations) ਆਦਿ ਨਾਲ ਵਾਪਰਦੀਆਂ ਹਨ । ਮਿਸਾਲ ਵਜੋਂ ਅੰਤ ਦਾ ਠੰਡਾ ਮੌਸਮ ਫੁੱਟ ਬਾਈਟ (ਪੈਰ ਗਲ ਜਾਣਾ ਅਤੇ ਉੱਚਾ ਤਾਪਮਾਨ, ਹੀਟ ਕਰੈਂਮਪ, ਅਜਿਹੀਆਂ ਅਪੰਗਤਾਵਾਂ ਨੂੰ ਜਨਮ ਦਿੰਦੇ ਹਨ । ਕੰਮ ਦੇ ਸਥਾਨ ਤੇ ਉੱਚੀਆਂ ਅਵਾਜ਼ਾਂ ਜਾਂ ਰੌਲੇ ਕਾਰਨ ਬੋਲਾਪਣ ਹੋ ਸਕਦਾ ਹੈ ।

2. ਸਮਾਜਿਕ ਕਾਰਨ (Social Factor) – ਬਹੁਤ ਸਾਰੀਆਂ ਸਮਾਜਿਕ ਅਸਮਰਥਾ ਕੰਮ ਕਰਨ ਵਾਲਿਆਂ ਵਿਚ ਉਦੋਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਜਦ ਉਹ ਸਮਾਜਿਕ ਵਾਤਾਵਰਣ ਵਿਚ ਆਪਣੇ ਆਪ ਨੂੰ ਢਾਲ ਨਹੀਂ ਪਾਉਂਦੇ । ਇਹ ਕਈ ਵਾਰ ਆਪਣੇ-ਆਪ (Introvert) ਸੁਭਾਅ ਦੇ ਵਿਅਕਤੀਆਂ ਵਿਚ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਉਹ ਕੰਮ ਕਰਤਾ ਜੋ ਆਪਣੇ ਆਪ ਨੂੰ ਸਮਾਜ ਅਨੁਸਾਰ ਨਾ ਢਾਲ ਸਕੇ ਤਾਂ ਕਈ ਪ੍ਰੇਸ਼ਾਨੀਆਂ ਜਿਵੇਂ ਕਿ ਉਦਾਸੀ, ਤਣਾਅ, ਚਿੰਤਾ ਅਤੇ ਅਸੁਰੱਖਿਆ ਦੇ ਹੇਠ ਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੇ ਹੋਰ ਵੀ ਕਾਰਨ ਹਨ : ਜਿਵੇਂ ਕਿ ਆਪਣੇ ਆਪ ਵਿਚ ਰਹਿਣਾ, · ਆਤਮਵਿਸ਼ਵਾਸ ਦੀ ਕਮੀ ਅਤੇ ਬੁਰੇ ਰਿਸ਼ਤੇ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 3.
ਆਮ ਪੇਸ਼ੇਵਰ ਬਿਮਾਰੀਆਂ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ।
ਉੱਤਰ-
ਆਕੂਪੇਸ਼ਨਲ ਸੇਫਟੀ ਐਂਡ ਹੈਲਥ ਕੰਨਵੈਨਸ਼ਨ (Occupational safety and health Convention) ਦੇ ਅਨੁਸਾਰ ਕਿੱਤਾ ਬਿਮਾਰੀ’ ਸ਼ਬਦ ਉਹਨਾਂ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਨੂੰ ਕਵਰ ਕਰਦਾ ਹੈ ਜੋ ਕਿ ਕੰਮ ਦੀਆਂ ਗਤੀਵਿਧੀਆਂ ਤੋਂ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਜ਼ਖ਼ਮਾਂ ਦੇ ਐਕਸਪੋਜਰ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਆਉਂਦੇ ਹਨ । ਕਿੱਤਾ ਸੰਬੰਧੀ ਬਹਤ ਅਤੇ ਭਿੰਨ-ਭਿੰਨ ਬਿਮਾਰੀਆਂ ਹਨ ਜੋ ਕਿ ਵੱਖ-ਵੱਖ ਰੋਜ਼ਗਾਰ ਕੰਮਾਂ ਵਿਚੋਂ ਘਟਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚੋਂ ਕੁੱਝ ਬਿਮਾਰੀਆਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਦੱਸਿਆ ਗਿਆ ਹੈ ।

ਭੌਤਿਕ ਕਾਰਨਾਂ ਕਰਕੇ ਪੈਦਾ ਹੋਏ ਰੋਗ (Diseases due to Physical agents)
ਧੂੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Dust Diseases or Dust hazard)
ਰਸਾਇਣਿਕ ਤੱਤਾਂ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Chemical diseases or chemical hazards)
ਅਸਧਾਰਨ ਸਮੇਂ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਪੈਦਾ ਹੋਏ ਰੋਗ ।

ਪਸ਼ਨ 4.
ਕਿਵੇਂ ਭੌਤਿਕ ਏਜੰਟ ਕਿੱਤੇ ਦੀ ਬਿਮਾਰੀ ਦਾ ਕਾਰਨ ਹੋ ਸਕਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਸ ਸ਼੍ਰੇਣੀ ਵਿਚ ਉਹ ਬਿਮਾਰੀਆਂ ਆਉਂਦੀਆਂ ਹਨ ਜੋ ਕੰਮ ਕਰਨ ਵਾਲੇ ਸਥਾਨ ਤੋਂ ਉੱਚੇ ਅਤੇ ਨੀਵੇਂ ਤਾਪਮਾਨ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਬਹੁਤ ਉਦਯੋਗਿਕ ਕਰਮਚਾਰੀ ਜੋ ਕਿ ਬਹੁਤ ਹੀ ਗਰਮ ਤਾਪਮਾਨ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਕੋਲੇ ਦੀਆਂ ਖਾਣਾਂ ਦੇ ਭੱਠੇ ਆਦਿ ਵਿਚ ਚਿਹਰੇ ਦਾ ਜਲਣਾ, ਕੈਮਪ ਜਾਂ ਥਕਾਵਟ ਆਦਿ ਬਿਮਾਰੀਆਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ਅਤੇ ਜੋ ਉਦਯੋਗਿਕ ਕਰਮਚਾਰੀ ਬਹੁਤ ਹੀ ਠੰਡੇ ਤਾਪਮਾਨ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਫੋਰਸਟ ਬਾਈਟ, ਪੈਰਾਂ ਦਾ ਗਲਣਾ ਆਦਿ ਸਮੱਸਿਆਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਇਹਨਾਂ ਤੋਂ ਇਲਾਵਾ ਕੁਝ ਹੋਰ ਵੀ ਭੌਤਿਕ ਕਾਰਕ ਹਨ ਜੋ ਕਿ ਅੱਗੇ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

(ਉ) ਰੋਸ਼ਨੀ (Light) – ਤੇਜ਼ ਰੋਸ਼ਨੀ ਜਾਂ ਘੱਟ ਰੋਸ਼ਨੀ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਅੱਖਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । ਜਿੱਥੇ ਤੇਜ਼ ਰੋਸ਼ਨੀ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਮਾਨਸਿਕ ਥਕਾਵਟ ਹੁੰਦੀ ਹੈ ਉੱਥੇ ਹੀ ਘੱਟ ਰੋਸ਼ਨੀ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਸਿਰ ਦਰਦ, ਅੱਖਾਂ ਤੇ ਭਾਰੀਪਨ ਅਤੇ ਮਾਨਸਿਕ ਦਬਾਅ ਵਰਗੀਆਂ ਸਮੱਸਿਆਵਾਂ | ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ ।

(ਅ) ਰੌਲਾ (Noise) – ਤੇਜ਼ ਰੌਲੇ ਵਿਚ ਕੰਮ ਕਰਨ ਅਤੇ ਉੱਚੀ ਅਵਾਜ਼ ਵਿਚ ਸੁਣਨ ਨਾਲ ਸੁਣਨ ਸ਼ਕਤੀ, ਸਿਰ ਦਰਦ ਅਤੇ ਤਣਾਅ ਆਦਿ ਪੈਦਾ ਹੋ ਜਾਂਦੇ ਹਨ ।

(ਇ) ਰੇਡੀਏਸ਼ਨ (Rediation) – ਵਿਕਿਰਣਾਂ ਨਾਲ ਆਦਰਾਂ ਦੇ ਤੱਲ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਦਾ ਹੈ ਜਿਸ ਨਾਲ ਉਲਟੀਆਂ, ਖੂਨ ਦੀ ਉਲਟੀਆਂ ਅਤੇ ਦਸਤ ਲੱਗ ਜਾਂਦੇ ਹਨ । ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਰੇਡੀਏਸ਼ਨ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਕੈਂਸਰ ਅਤੇ ਕਾਰਡੀਉਵੈਸਕੂਲਰ ਨਾਮਕ ਬਿਮਾਰੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਵੱਖ-ਵੱਖ ਧੂੜ ਕਾਰਕਾਂ ਨੂੰ ਉਜਾਗਰ ਕਰੋ ਜੋ ਕਿ ਰੋਗਾਂ ਦਾ ਕਾਰਨ ਬਣ ਸਕਦੇ ਹਨ ?
ਉੱਤਰ-
ਧੂੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Dust Diseases) – ਫੇਫੜਿਆਂ ਦੀਆਂ ਅਜਿਹੀਆਂ ਕਈ ਬਿਮਾਰੀਆਂ ਹਨ ਜੋ ਧੂੜ ਦੇ ਸਰੀਰ ਵਿਚ ਜਾਣ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਧੁੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਕੁਝ ਕੁ ਰੋਗ ਹੇਠ ਲਿਖੇ ਹਨ-

(ੳ) ਕੋਲੇ ਦੀ ਧੂੜ (Coal Dust) – ਕਾਲੇ ਫੇਫੜਿਆਂ ਦੀ ਬਿਮਾਰੀ ਕੋਲੇ ਨੂੰ ਸਾਹ ਦੁਆਰਾ ਅੰਦਰ ਲੈ ਜਾਣ ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚ ਜਲਣ ਅਤੇ ਸੋਜ ਹੁੰਦੀ ਹੈ । ਇਹ ਇਕ ਸਥਾਈ ਬਿਮਾਰੀ ਹੁੰਦੀ ਹੈ ਜੋ ਫੇਫੜਿਆਂ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਂਦੀ ਹੈ ਅਤੇ ਸਾਹ ਲੈਣ ਵਿਚ ਮੁਸ਼ਕਿਲ ਪੈਦਾ ਕਰਦੀ ਹੈ ।

(ਅ) ਸਿਲਿਕਾ ਧੂੜ (Silica Dust) – ਇਹ ਸਥਿਤੀ ਉਦੋਂ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਸਿਲਿਕਾ ਟਿਲ ਖਾਂਣਾਂ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹੋਏ ਸਾਹ ਦੁਆਰਾ ਸਰੀਰ ਵਿਚ ਪਹੁੰਚਦੇ ਹਨ । ਇਸ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚ ਜਲਣ ਹੁੰਦੀ ਹੈ ਅਤੇ ਹੋਰ ਵੀ ਕਈ ਫੇਫੜਿਆਂ ਸੰਬੰਧੀ ਰੋਗ ਪੈਦਾ ਹੋ ਜਾਂਦੇ ਹਨ ।

(ਈ) ਕਪਾਹ ਦੀ ਧੂੜ/ਬਿਸੀਨੋਸਿਸ (Cotton dust/Byssinosis) – ਇਸਨੂੰ ਭੂਰਾ ਫੇਫੜਾ (Brown lung) ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਹ ਉਦੋਂ ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਕਰਮਚਾਰੀ ਭੰਗ, ਗਣ ਅਤੇ ਕਪਾਹ ਦੀ ਸੋਸਿੰਗ ਦੇ ਕੰਮ ਦੇ ਦੁਆਰਾ ਧੂੜ ਨੂੰ ਸਾਹ, ਦੁਆਰਾ ਸਰੀਰ ਦੇ ਅੰਦਰ ਲੈਂਦਾ ਹੈ । ਇਹ ਇਕ ਭਿਅੰਕਰ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਛਾਤੀ ਤੰਗ ਜਾਂ ਜਕੜ ਜਾਂਦੀ ਹੈ ਅਤੇ ਸਾਹ ਦੀ ਕਮੀ ਹੋਣ ਲੱਗਦੀ ਹੈ । ਇਹ ਮੁੱਖ ਕਰਕੇ ਟੈਕਸਟਾਈਲ ਦੀਆਂ ਫੈਕਟਰੀਆਂ ਵਿਚ ਕੱਪੜਿਆਂ ਦਾ ਕੰਮ-ਕਾਜ ਕਰਦੇ ਹਨ ।

(ਸ) ਕਿੱਤਾ ਅਸਥਮਾ (Occupation Asthma) – ਇਹ ਦਮਾਂ ਧੂੜ, ਗੈਸਾਂ, ਧੂੰਆਂ ਅਤੇ ਵਾਸ਼ਪ ਆਦਿ ਵਿਚ ਸਾਹ ਲੈਣ ਕਾਰਨ ਹੁੰਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਦਮੇ ਦੇ ਲੱਛਣ ਭਿਅੰਕਰ ਖੰਘ ਅਤੇ ਘਬਰਾਹਟ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਵੱਖ-ਵੱਖ ਰਸਾਇਣਕ ਖਤਰਿਆਂ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰੋ ਜੋ ਕਿ ਬਿਮਾਰੀਆਂ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਹਨ ?
ਉੱਤਰ-
ਸਾਡੀ ਰੋਜ਼ਾਨਾ ਦੀ ਜ਼ਿੰਦਗੀ ਅਤੇ ਉਦਯੋਗਾਂ ਵਿਚ ਵਿਆਪਕ ਤੌਰ ਤੇ ਰਸਾਇਣ ਵਰਤੇ ਜਾਂਦੇ ਹਨ | ਕਈ ਕੰਮ ਵਿਚ ਆਉਣ ਵਾਲੇ ਉਤਪਾਦ ਰਸਾਇਣਾਂ ਤੋਂ ਬਣਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਪਲਾਸਟਿਕ, ਪੇਂਟਸ, ਫਾਰਮੇਟਿਕਲ, ਡਿਟਰਜੈਂਟ ਆਦਿ | ਕਈ ਰਸਾਇਣਾਂ ਦਾ ਅਸਰ ਲੰਬੇ ਸਮੇਂ ਦੇ ਇਸਤੇਮਾਲ ਤੋਂ ਬਾਅਦ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ । ਇਸ ਵਿਚ ਡਾਇਬਟੀਜ਼, ਐਲਰਜੀ, ਦਮਾ, ਐਕਜ਼ੀਮਾ, ਕੈਂਸਰ, ਧਿਆਨ ਦੀ ਕਮੀ, ਸਿੱਖਣ ਵਿਚ ਕਮੀ, ਬਾਂਝਪਨ, ਡਿਪਰੈਸ਼ਨ, ਗੰਭੀਰ ਥਕਾਵਟ, ਰਸਾਇਣਿਕ ਸੰਵੇਦਨਸ਼ੀਲਤਾ, ਦਿਲ ਦੀ ਬਿਮਾਰੀ, ਮਲਟੀਪਲ ਸਕਲਰੋਸਿਸ, ਪਾਰਕਿੰਸਨਾਸ ਦੀ ਬਿਮਾਰੀ, ਥਾਈਰੋਡ ਬਿਮਾਰੀ ਆਦਿ ਰਸਾਇਣਿਕ ਤੱਤਾਂ ਤੋਂ ਹੋਣ ਵਾਲੀਆਂ ਬਿਮਾਰੀਆਂ ਹਨ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕੁਝ ਹੋਰ ਬਿਮਾਰੀਆਂ ਵੀ ਹਨ ਜੋ ਕਿ ਅੱਗੇ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

(ਉ) ਜ਼ਹਿਰੀਲੀਆਂ ਗੈਸਾਂ ਨੂੰ ਸੁੰਘਣ ਨਾਲ ਹੋਣ ਵਾਲੀਆਂ ਬਿਮਾਰੀਆਂ-ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਗੈਸਾਂ ਜਿਵੇਂ ਕਿ ਕਲੋਰੀਨ (Chlorine), ਫਾਸਗਿਨ (Phosgene), ਸਲਫਰਡਾਈਆਕਸਾਈਡ (Sulphurdioxide), ਹਾਈਡਰੋਜਨ, ਗਿਲਫਾਇਡ, ਨਾਈਟ੍ਰੋਜਨ ਡਾਈਆਕਸਾਈਡ ਅਤੇ ਅਮੋਨੀਆ ਆਦਿ । ਜੇਕਰ ਅਚਾਨਕ ਉਦਯੋਗਿਕ ਹਾਦਸੇ ਵਿਚ ਲੀਕ ਹੋ ਜਾਵੇ ਤਾਂ ਇਹ ਬੁਰੀ ਤਰ੍ਹਾਂ ਫੇਫੜਿਆਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਜਿਵੇਂ ਕਿ ਕਲੋਰੀਨ ਅਤੇ ਅਮੋਨੀਆ ਨਾਮਕ ਗੈਸਾਂ ਆਸਾਨੀ ਨਾਲ ਸਰੀਰ ਅੰਦਰ ਦਾਖਿਲ ਹੋ ਕੇ ਮੂੰਹ, ਨੱਕ ਅਤੇ ਗਲੇ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀਆਂ ਹਨ ।

(ਅ) ਲੀਡ ਜ਼ਹਿਰ (Lead Poisoning) – ਲੀਡ ਜ਼ਹਿਰ ਦੇ ਛੋਟੇ-ਛੋਟੇ ਕਣਾਂ ਦੇ ਸਰੀਰ ਵਿਚ ਜਾਣ ਨਾਲ, ਇਕ ਕਰਮਚਾਰੀ ਨੂੰ ਪੇਟ ਦੀ ਕਬਜ਼ੀ, ਅਨੀਮੀਆ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਵਿਚ ਦਰਦ ਹੋ ਸਕਦਾ ਹੈ ।

(ਈ) ਮਰਕਿਊਰੀ ਜ਼ਹਿਰ (Mercury Poisoning) – ਮਰਕਿਊਰੀ ਜ਼ਹਿਰ ਦੇ ਸਰੀਰ ਵਿਚ ਦਾਖਲ ਹੋਣ ਨਾਲ ਸਾਹ ਲੈਣ ਵਿਚ ਤਕਲੀਫ, ਮਸੂੜਿਆਂ ਵਿਚ ਸੋਜ਼, ਦੰਦ ਡਿੱਗਣ, ਅਨੀਮੀਆ ਆਦਿ ਦੀ ਤਕਲੀਫ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਅਸਮਰਥਾ ਦੇ ਕੋਈ ਵੀ ਦੋ ਬਚਾਅ ਦੇ ਉਪਾਅ ਦਿਓ ।
ਉੱਤਰ-
1. ਕੰਮ ਕਰਨ ਦੇ ਸਥਾਨ ਦਾ ਰੱਖ-ਰਖਾਉ (Maintenance of working Place) – ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਭੌਤਿਕ ਏਜੰਟਾਂ ਦੇ ਕਾਰਨ ਜਿਵੇਂ ਗਰਮੀ, ਸਰਦੀ, ਦਬਾਅ, ਰੇਡੀਏਸ਼ਨ, ਰੌਲਾ ਆਦਿ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਇਹਨਾਂ ਭੌਤਿਕ ਏਜੰਟਾਂ ਦੇ ਰੱਖ-ਰਖਾਵ ਵੱਲ ਖਾਸ ਧਿਆਨ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਕ ਮੁਆਇਨ ਕਰਤਾ ਨੂੰ ਠੰਡੇ, ਹਲਕੇ, ਹਵਾਦਾਰ ਤਾਪਮਾਨ ਅਤੇ ਨਮੀ ਦੀ ਜਾਂਚ ਅਤੇ ਸਾਂਭ-ਸੰਭਾਲ ਨੂੰ ਚੈੱਕ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਵਾਸਤੇ ਹੇਠ ਲਿਖੇ ਕਦਮ ਚੁੱਕੇ ਜਾਣੇ ਚਾਹੀਦੇ ਹਨ ।

2. ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਤੇ ਰੋਕ (Control of air Pollution) – ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਕਾਰਨ ਹੁੰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਨੂੰ ਰੋਕਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖਿਆਂ ਤੇ ਨੋਟ ਲਿਖੋ ।
(ਉ) ਸੁਰੱਖਿਆ ਯੰਤਰਾਂ ਦੀ ਵਰਤੋਂ
(ਅ) ਕਾਮਿਆਂ ਦੀ ਸਿੱਖਿਆ ।
ਉੱਤਰ-
(ੳ) ਸੁਰੱਖਿਆ ਯੰਤਰਾਂ ਦੀ ਵਰਤੋਂ (Use of protective Devices) – ਕਈ ਕਾਰੋਬਾਰੀ ਅਸਮਰਥਾਵਾਂ ਨੂੰ ਸੁਰੱਖਿਆ ਉਪਕਰਨ ਦੀ ਵਰਤੋਂ ਨਾਲ ਘਟਾਇਆ ਜਾ ਸਕਦਾ ਹੈ , ਜਿਵੇਂ ਕਿ ਗੈਸ ਮਾਸਕ (ਮਖੋਟਾ) ਸਾਹ ਵਾਲੀਆਂ ਅਸਮਰਥਾਵਾਂ ਤੋਂ ਬਚਾ ਕਰ ਸਕਦਾ ਹੈ ਜੋ ਕਿ ਧੂੜ, ਗੈਸਾਂ ਆਦਿ ਰਸਾਇਣਿਕ ਪਦਾਰਥਾਂ ਦੇ ਸਾਹ ਦੁਆਰਾ ਅੰਦਰ ਲੈਣ ਨਾਲ ਉਤਪੰਨ ਹੁੰਦੀਆਂ ਹਨ | ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਸੁਰੱਖਿਆ ਯੰਤਰ ਜਿਵੇਂ ਕਿ ਕੰਨਾਂ ਦੇ ਪਲੱਗ, ਜੁੱਤੇ, ਦਸਤਾਨੇ, ਐਪਰਨ, ਹੈਲਮੇਟ ਆਦਿ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਕਿੱਤਾ ਸੰਬੰਧੀ ਸਮੱਸਿਆਵਾਂ ਤੋਂ ਬਚਾਉਂਦੇ ਹਨ ।

(ਅ) ਕਾਮਿਆਂ ਦੀ ਸਿੱਖਿਆ (Educating the Workers) – ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਕਾਰੋਬਾਰੀ ਦੁਰਘਟਨਾਵਾਂ ਅਤੇ ਅਸਮਰਥਾਵਾਂ ਸਿੱਖਿਆ ਦੀ ਘਾਟ ਕਾਰਨ ਹੁੰਦੀਆਂ ਹਨ । ਹਰ ਕਰਮਚਾਰੀ ਨੂੰ ਸੁਰੱਖਿਆ ਯੰਤਰਾਂ ਦੀ ਉੱਚਿਤ ਵਰਤੋਂ ਬਾਰੇ ਸਿੱਖਿਆ ਦੇਣੀ ਚਾਹੀਦੀ ਹੈ । ਕਾਮਿਆਂ ਨੂੰ ਮਸ਼ੀਨਾਂ ਦੀ ਠੀਕ ਢੰਗ ਨਾਲ ਵਰਤੋਂ ਕਰਨ ਸੰਬੰਧੀ ਸਿਖਲਾਈ ਦੇਣੀ ਚਾਹੀਦੀ ਹੈ । ਹਰ ਕਾਮੇ ਨੂੰ ਉਸਦੇ ਕੰਮ-ਮਾਹੌਲ ਵਿਚ ਆਉਣ ਵਾਲੇ ਖ਼ਤਰਿਆਂ ਅਤੇ ਉਨ੍ਹਾਂ ਤੋਂ ਬਚਣ ਦੀ ਸਿਖਲਾਈ ਦੇਣੀ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਮੁੜ-ਵਸੇਬੇ ਲਈ ਡਬਲਿਊ. ਐਚ. ਓ. ਵਲੋਂ ਦਿੱਤੀ ਪਰਿਭਾਸ਼ਾ ਨੂੰ ਬਿਆਨ ਕਰੋ !
ਉੱਤਰ-
ਡਬਲਯੂ. ਐੱਚ. ਓ. (W.H.O.) ਦੇ ਅਨੁਸਾਰ, “ਪੁਨਰ ਵਿਸਥਾਪਨ ਜਾਂ ਮੁੜ ਵਸੇਬਾ ਅਪੰਗ ਵਿਅਕਤੀ ਵਿਚ ਕੰਮ ਕਰਨ ਦੀ ਉਚਤਮ ਯੋਗਤਾ ਪੈਦਾ ਕਰਨ ਦੇ ਉਦੇਸ਼ ਹਿੱਤ ਉਸਦੀ ਪੁਨਰਸਿਖਲਾਈ ਲਈ ਡਾਕਟਰੀ, ਸਮਾਜਿਕ, ਵਿੱਦਿਅਕ ਅਤੇ ਕਿੱਤਾਕਾਰੀ ਢੰਗਾਂ ਦੀ ਸਮੁੱਚੀ ਅਤੇ ਸੰਯੁਕਤ ਵਰਤੋਂ ਹੈ । ਉਦਾਹਰਨ ਵਜੋਂ ਇਕ ਵਿਅਕਤੀ ਕਿਸੇ ਸੱਟ ਨਾਲ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਗੁਆ ਬੈਠਦਾ ਹੈ । ਉਸਦੀ ਤੰਦਰੁਸਤੀ ਨੂੰ ਵਾਪਿਸ ਲਿਆਉਣ ਲਈ ਕੀਤੇ ਕੰਮ ਪੁਨਰ ਵਿਸਥਾਪਨ ਅਖਵਾਉਂਦਾ ਹੈ । ਪੁਰਾਣੇ ਸਮਿਆਂ ਵਿੱਚ ਅਸਮਰਥ ਵਿਅਕਤੀ ਨੂੰ ਸਮਾਜ ਵਲੋਂ ਅਣਗੌਲਾ ਕਰ ਦਿੱਤਾ ਜਾਦਾ ਸੀ ਪਰੰਤੂ ਅੱਜਕੱਲ੍ਹ ਅਸਮਰਥ ਨੂੰ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਵਿਚ ਵਾਪਸ ਲਿਆਉਣ ਲਈ ਕੀਤੇ ਕੰਮਾਂ ਨੂੰ ਪੁਨਰਵਿਸਥਾਪਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਅਸਮਰਥਾਂ ਨੂੰ ਕਿੱਤਾਕਾਰੀ ਦੀ ਸਿਖਲਾਈ ਵੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਸਿੱਖਿਆ ਨੂੰ ਕਿੱਤਾਕਾਰੀ ਸਿਖਲਾਈ (Vocational training) ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਮੁੜ-ਵਸੇਬੇ ਦੇ ਖੇਤਰ ਨੂੰ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ-
ਮੁੜ-ਵਸੇਬੇ ਦਾ ਖੇਤਰ ਬਹੁਤ ਹੀ ਵਿਸ਼ਾਲ ਹੈ । ਕਿਉਂਕਿ ਦੁਰਘਟਨਾਵਾਂ ਕਾਰਨ ਮੁੜ ਵਸੇਬੇ ਦੀ ਲੋੜ ਮਹਿਸੂਸ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਪੁਨਰ ਵਿਸਥਾਪਨ ਦੇ ਖੇਤਰ ਨੂੰ ਹੇਠ ਲਿਖੇ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ-

ਡਾਕਟਰੀ ਮੁੜ-ਵਸੇਬਾ (Medical Rehabilitation) – ਕਿਸੇ ਸੱਟ ਜਾਂ ਬਿਮਾਰੀ ਨਾਲ ਆਏ ਕਿਸੇ ਸਰੀਰਕ ਵਿਗਾੜ ਦੀ ਸੂਰਤ ਵਿਚ ਮਾਹਿਰ ਡਾਕਟਰੀ ਸਹਾਇਤਾ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ । ਇਸ ਵਿਚ ਮੈਡੀਕਲ ਬਾਂਚ, ਸਰਜਰੀ, ਆਰਥੋਪੈਡਿਕ ਅਤੇ ਫਿਜ਼ੀਉਥੇਰੈਪੀ ਸ਼ਾਮਿਲ ਹਨ ।
ਕਿੱਤਾਕਾਰੀ ਮੁੜ-ਵਸੇਬਾ (Vocational Rehabilitation) – ਅਸਮਰਥਾ ਦੇ ਬਾਵਜੂਦ, ਅਸਮਰਥਾਂ ਨੂੰ ਆਪਣੀ ਰੋਜ਼ੀ ਕਮਾਉਣ ਲਈ ਕਿੱਤਾਕਾਰੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਮਿਸਾਲ ਦੇ ਤੌਰ ਤੇ ਅੰਨਿਆਂ ਨੂੰ ਕੁਰਸੀ ਬੁਣਨ ਦੀ ਸਿਖਲਾਈ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।
ਸਮਾਜਿਕ ਮੁੜ-ਵਸੇਬਾ (Social Rehabilitation) – ਇਸ ਨਾਲ ਅਸਮਰਥ ਵਿਅਕਤੀ ਦੇ ਪਰਿਵਾਰਕ ਅਤੇ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਬਹਾਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਉਸਦੀ ਅਪਾਹਜਤਾ ਦੇ ਬਾਵਜੂਦ ਉਸਦੇ ਸਮਾਜਿਕ ਰੁਤਬੇ ਨੂੰ ਹੁਲਾਰਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਮਨੋਵਿਗਿਆਨਿਕ ਮੁੜ ਵਸੇਬਾ (Psychological Rehabilitation) – ਇਸ ਵਿਚ ਅਸਮਰਥ ਵਿਅਕਤੀ ਦਾ ਆਤਮ-ਵਿਸ਼ਵਾਸ ਬਹਾਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਦਿਮਾਗੀ ਵਿਗਾੜ ਦੇ ਜਾਂ ਦਬਾਉ ਦੀ ਸੂਰਤ ਵਿਚ ਮਨੋਚਕਿਸਤਾ ਵਿਭਾਗ, ਮਨੋਵਿਗਿਆਨਕ ਮੁੜ ਵਸੇਬੇ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਹੇਠ ਲਿਖਿਆਂ ‘ਤੇ ਨੋਟ ਲਿਖੋ ।
(ਉ) ਹਿੰਦ ਕੁਸ਼ਟ ਨਿਵਾਰਨ ਸਿੰਘ
(ਅ) ਕਾਮਯਨੀ ਸਕੂਲ ।
ਉੱਤਰ-
(ਉ) ਹਿੰਦ ਕੁਸ਼ਟ ਨਿਵਾਰਣ ਸੰਘ (Hind Kusht Nivaran Sangh) – ਇਹ ਨਵੀਂ ਦਿੱਲੀ ਵਿਖੇ 1950 ਵਿੱਚ ਬਣਾਈ ਗਈ ਸੀ । ਇਹ ਸੰਘ ਵਿਸ਼ੇਸ਼ ਤੌਰ ਤੇ ਕੋਹੜੀਆਂ ਲਈ ਕੰਮ ਕਰਦਾ ਹੈ । ਹਿੰਦ ਕੁਸ਼ਟ ਨਿਵਾਰਣ ਸੰਘ ਦੇਸ਼ ਭਰ ਵਿੱਚ ਕਈ ਕੋਹੜ ਕਲੀਨਿਕਾਂ ਨੂੰ ਮਾਲੀ ਮਦਦ ਵੀ ਦਿੰਦਾ ਹੈ । ਇਸ਼ਤਿਹਾਰਾਂ ਰਾਹੀਂ ਇਹ ਸੰਸਥਾ ਕੋਹੜੀਆਂ ਦੀ ਭਲਾਈ ਲਈ ਲੋਕਾਂ ਨੂੰ ਸਿੱਖਿਅਤ ਕਰਦੀ ਹੈ । ਕੋਹੜ ਇੱਕ ਕੌਨਿਕ ਛੂਤਛਾਤ ਦੀ ਬਿਮਾਰੀ ਹੈ ਜੋ ਕਿ ਚਮੜੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ । ਇਹ ਸੰਸਥਾ ਇੱਕ ਮੈਗਜ਼ੀਨ ‘‘ਲੈਪਰੋਸੀ ਇੰਨ ਇੰਡੀਆ” ਵੀ ਪ੍ਰਕਾਸ਼ਿਤ ਕਰਦੀ ਹੈ ।

(ਅ) ਕਾਮਯਨੀ ਸਕੂਲ (Kamayani School) – ਇਹ ਸਕੂਲੇ ਪੂਨਾ ਵਿਖੇ 1964 ਵਿੱਚ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਸੀ । ਇਸ ਸਕੂਲ ਵਿੱਚ ਅਪਾਹਜ, ਖ਼ਾਸ ਤੌਰ ‘ਤੇ ਦਿਮਾਗੀ ਤੌਰ ‘ਤੇ ਕਮਜ਼ੋਰਾਂ ਨੂੰ ਕਿੱਤਾ ਸਿਖਲਾਈ ਜਿਵੇਂ ਫਰਨੀਚਰ ਨੂੰ ਪਾਲਿਸ਼ ਕਰਨੀ ਆਦਿ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।

ਪੰਜ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ ਤੋਂ (Five Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਅਸਮਰਥਾ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਅਸਮਰਥਾ ਦੀਆਂ ਕਿਸਮਾਂ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ-
ਅਸਮਰਥਾ ਦਾ ਅਰਥ ਹੈ, ਕੋਈ ਵਿਸ਼ੇਸ਼ ਸਰੀਰਕ ਜਾਂ ਮਾਨਸਿਕ ਕੰਮ ਕਰਨ ਦੀ ਅਯੋਗਤਾ । ਜਦੋਂ ਸਰੀਰਕ ਮਾਨਸਿਕ ਕਾਰਜ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਘੱਟ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇਸ ਅਵਸਥਾ ਨੂੰ ਅਸਮਰਥਤਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਡਬਲਯੂ. ਐੱਚ. ਓ. ਅਨੁਸਾਰ (W.H.O.), ‘ ‘ ਇਕ ਸਿਹਤਮੰਦ ਅਤੇ ਸਧਾਰਨ ਵਿਅਕਤੀ ਲਈ ਨਿਰਧਾਰਿਤ ਕੰਮ ਕਰਨ ਵਿਚ ਆਈ ਰੁਕਾਵਟ ਦੀ ਆਯੋਗਤਾ ਨੂੰ ਅਪਾਹਜਤਾ ਆਖਿਆ ਜਾਂਦਾ ਹੈ ।
ਅਸਮਰਥਤਾ ਦੀਆਂ ਕਿਸਮਾਂ (Types of Disability)
ਅਸਮਰਥਤਾ ਆਮਤੌਰ ਤੇ ਦੋ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ-

ਬਣਤਰ ਅਸਮਰਥਾ (Structural Disability)
ਕਾਰਜਾਤਮਿਕ ਅਸਮਰਥਾ (Functional Disability) ।

1. ਬਣਤਰ ਅਸਮਰਥਤਾ (Structural Disability) – ਇਹ ਅਸਮਰਥਤਾ ਸਰੀਰਕ ਬਣਤਰ ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ । ਇਸ ਵਿਚ ਸਰੀਰ ਦਾ ਬੇਢੰਗਾ ਅਤੇ ਕਰੂਪਤਾ ਆਉਂਦੇ ਹਨ | ਸਰੀਰ ਦੀ ਇਹ ਹਾਲਤ ਕਿਸੇ ਵੀ ਐਕਸੀਡੈਂਟ ਜਾਂ ਸੱਟ ਨਾਲ ਹੋ ਸਕਦੀ ਹੈ । ਇਸ ਦੇ ਕਈ ਕਾਰਨ ਹੋ ਸਕਦੇ ਹਨ ਜਿਵੇਂ, ਦੁਰਘਟਨਾਵਾਂ, ਅਸੰਤੁਲਿਤ ਖੁਰਾਕ ਅਤੇ ਕੰਮ ਕਰਦੇ ਸਮੇਂ ਕੀਤੀਆਂ ਗਲਤੀਆਂ | ਸਰੀਰਕ ਬਣਤਰ ਦੇ ਅਨੁਸਾਰ ਹੇਠ ਲਿਖੀਆਂ ਅਪੰਗਤਾਵਾਂ ਆਉਂਦੀਆਂ ਹਨ ।

(ਉ) ਕਾਈਫੋਸਿਸ (Kyphosis)-ਇਹ ਅਸਮਰਥਤਾ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਦੇ ਪਿੱਠ ਵਾਲੇ ਪਾਸੇ ਡਰੋਸਲ ਵਿਚ ਹੋਏ ਵਾਧੇ ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਪਿੱਠ ਵਿਚ ਕੁੱਬ ਪੈ ਜਾਂਦਾ ਹੈ ।
(ਅ) ਲੋਰਡੋਸਿਸ (Lordosis)-ਇਹ ਅਸਮਰਥਤਾ, ਲੱਕ ਵਾਲੇ ਪਾਸੇ ਆਏ ਵਾਧੇ ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਸਰੀਰ ਦੇ ਉੱਪਰਲੇ ਭਾਗ ਵਿਚ ਅੱਗੇ ਵੱਲ ਝੁਕਾਅ ਆ ਜਾਂਦਾ ਹੈ ।
(ਇ) ਸਕੌਲਸਿਸ (Scoliosis)-ਇਹ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਦੇ ਲਟੇਰਲ ਵਿਚ ਆਏ ਵਾਧੇ ਨਾਲ ਹੁੰਦਾ ਹੈ ।

2. ਕਾਰਜਾਤਮਿਕ ਅਸਮਰਥਤਾ (Functional Disability) – ਇਸ ਕਿਸਮ ਦੀ ਅਸਮਰਥਤਾ ਵਿਚ ਸਰੀਰਕ ਅੰਗ | ਪ੍ਰਭਾਵਿਤ ਹੋ ਜਾਂਦੇ ਹਨ ।ਇਹ ਨੁਕਸ ਆਮ ਕਰਕੇ ਲੰਬੀ ਬਿਮਾਰੀਆਂ ਕਾਰਨ ਹੁੰਦੇ ਹਨ । ਸਾਹ ਦੀ ਬਿਮਾਰੀ, ਸਿੱਲੀਕੋਸਿਸ, ਐਸਬੈਗਸ, ਲੀਡ ਕਹਿਰ, ਸਾਈਡਰੋਸਿਸ, ਬਾਈਸਨੋਸਿਸ, ਲੇਬਰੋਸਿਸ, ਲੰਗ ਕੈਂਸਰ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਅਸਮਰਥਤਾਂ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ । ਅਸਮਰਥਤਾ ਨੂੰ ਪ੍ਰਵਾਭਿਤ ਕਰਨ ਵਾਲੇ ਕਾਰਕਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਅਸਮਰਥਤਾ ਦਾ ਅਰਥ ਹੈ, ਕੋਈ ਵਿਸ਼ੇਸ਼ ਸਰੀਰਕ ਜਾਂ ਮਾਨਸਿਕ ਕੰਮ ਕਰਨ ਦੀ ਅਯੋਗਤਾ । ਜਦੋਂ ਸਰੀਰਕ ਮਾਨਸਿਕ ਕਾਰਜ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਘੱਟ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇਸ ਅਵਸਥਾ ਨੂੰ ਅਸਮਰਥਤਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਅਸਮਰਥਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਕਾਰਕ (Factor of Causing Disability)
ਅਸਮਰਥਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਬਹੁਤ ਕਾਰਕ ਹਨ । ਇਹਨਾਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਸਮਝਿਆ ਗਿਆ ਹੈ-

1. ਮਾਨਸਿਕ ਤੱਤ (Mental Factor) – ਮਾਨਸਿਕ ਅਪੰਗਤਾ ਕਦੇ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ਪਰ ਕਈ ਵਾਰ ਇਹ ਮਾਨਸਿਕ ਤਨਾਅ ਕਾਰਨ ਵੀ ਹੋ ਸਕਦੀ ਹੈ | ਮਨ ਅਤੇ ਸਰੀਰ ਆਪਸ ਵਿਚ ਸੰਬੰਧਿਤ ਹੁੰਦੇ ਹਨ । ਇਸ ਲਈ ਮਾਨਸਿਕ ਤੱਤ ਸਰੀਰਕ ਸਥਿਤੀ ਨੂੰ ਬੁਰੀ ਤਰ੍ਹਾਂ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ ।

2. ਸਰੀਰਕ ਬਿਮਾਰੀ (Physical Disease) – ਸਰੀਰਕ ਬਿਮਾਰੀ ਜਾਂ ਬਿਮਾਰੀਆ ਦੇ ਕਾਰਨ ਕੁਝ ਕਮੀਆਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਜੋ ਕਿ ਅਸਮਰਥਤਾ ਦਾ ਕਾਰਨ ਬਣਦੀਆਂ ਹੈ ਜਿਵੇਂ ਕਿ ਚੇਚਕ ਦੀ ਬਿਮਾਰੀ ਕਾਰਨ ਅੰਨਾਪਨ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਅਸੀਂ ਇਹ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਰੀਰਕ ਬਿਮਾਰੀ ਅਪੰਗਤਾ ਦਾ ਕਾਰਨ ਹੋ ਸਕਦੀ ਹੈ ।

3. ਕਿੱਤੇ ਦੇ ਵਾਤਾਵਰਣ ਦੇ ਕਾਰਨ (Occupational Environment) – ਬਹੁਤ ਸਾਰੀਆਂ ਅਸਮਰਥਾਵਾਂ ਕੰਮ ਕਰਨ ਵਾਲੇ ਮਾਹੌਲ ਵਿਚ ਹੁੰਦੀਆਂ ਹਨ । ਜਿਵੇਂ ਕਿ ਸਾਹ ਦੀ ਅਪੰਗਤਾ, ਜ਼ਹਿਰੀਲੇ ਪਦਾਰਥ ਹਵਾ ਦੁਆਰਾ ਸਰੀਰ ਵਿਚ ਜਾਣ ਨਾਲ ਹੋ ਸਕਦੀ ਹੈ । ਜਿਵੇਂ ਕਿ ਐਸਬੈਮਟੋਲ ਫਾਇਬਰਜ਼ ਦੇ ਸਾਹ ਦੁਆਰਾ ਅੰਦਰ ਜਾਣ ਨਾਲ ਐਸਬੈਟਿਸਸ ਨਾਮਕ ਬਿਮਾਰੀ ਦਾ ਕਾਰਨ ਬਣਦਾ ਹੈ । ਕਈ ਵਾਰ ਸਰੀਰ ਦੀ ਗਲਤ ਸਥਿਤੀ (Postural) ਜਿਵੇਂ
ਕਿ ਗਲਤ ਬੈਠਕ, ਖੜ੍ਹੇ ਹੋਣ ਦੀ ਸਥਿਤੀ ਜਾ ਗਲਤ ਝੁਕਾਅ ਦੀਆਂ ਆਦਤਾਂ ਨਾਲ ਅਪੰਗਤਾ ਹੋ ਜਾਂਦੀ ਹੈ । | ਉਦਾਹਰਨ ਵਜੋਂ ਕਾਈਫੋਸਿਸ ਕੁੱਬਾਪਣ ਦਰਜ਼ੀਆਂ ਵਿਚ ਆਮ ਦੇਖਣ ਨੂੰ ਮਿਲਦਾ ਹੈ । ਕਿੱਤਾ ਸੰਬੰਧਿਤ ਕਈ
ਅਸਮਰਥਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

(ਉ) ਭੌਤਿਕ ਕਾਰਨ (Physical Factor) – ਬਹੁਤ ਸਾਰੀਆਂ ਅਸਮਰਥਾਵਾਂ ਭੌਤਿਕ ਕਾਰਨਾਂ ਜਿਵੇਂ ਕਿ ਗਰਮੀ, ਸਰਦੀ, ਰੋਸ਼ਨੀ, ਦਬਾਅ, ਰੌਲਾ, ਵਿਕੀਰਣਾਂ (Radiations) ਆਦਿ ਨਾਲ ਵਾਪਰਦੀਆਂ ਹਨ । ਮਿਸਾਲ ਵਜੋਂ-ਅੰਤ ਦਾ ਠੰਡਾ ਮੌਸਮ ਫੁੱਟ ਬਾਈਟ (ਪੈਰ ਗਲ ਜਾਣਾ ਅਤੇ ਉੱਚਾ ਤਾਪਮਾਨ, ਹੀਟ ਕਰੈਂਮਪ, ਅਜਿਹੀਆਂ ਅਸਮਰਥਾਵਾਂ ਨੂੰ ਜਨਮ ਦਿੰਦੇ ਹਨ । ਕੰਮ ਦੇ ਸਥਾਨ ਤੇ ਉੱਚੀਆਂ ਅਵਾਜ਼ਾਂ ਜਾਂ ਰੌਲੋਂ ਕਾਰਨ ਬੋਲਾਪਣ ਹੋ ਸਕਦਾ ਹੈ ।

(ਅ) ਸਮਾਜਿਕ ਕਾਰਨ (Social Factor) – ਬਹੁਤ ਸਾਰੀਆਂ ਸਮਾਜਿਕ ਅਸਮਰਥਾਵਾਂ ਕੰਮ ਕਰਨ ਵਾਲਿਆਂ ਵਿਚ ਉਦੋਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਜਦ ਉਹ ਸਮਾਜਿਕ ਵਾਤਾਵਰਣ ਵਿਚ ਆਪਣੇ ਆਪ ਨੂੰ ਢਾਲ ਨਹੀਂ ਪਾਉਂਦੇ । ਇਹ ਕਈ ਵਾਰ ਆਪਣੇ-ਆਪ (Introvert) ਸੁਭਾਅ ਦੇ ਵਿਅਕਤੀਆਂ ਵਿਚ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਉਹ ਕੰਮ ਕਰਤਾ ਜੋ ਆਪਣੇ ਆਪ ਨੂੰ ਸਮਾਜ ਅਨੁਸਾਰ ਨਾ ਢਾਲ ਸਕੇ ਤਾਂ ਕਈ ਪ੍ਰੇਸ਼ਾਨੀਆਂ ਜਿਵੇਂ ਕਿ ਉਦਾਸੀ, ਤਣਾਅ, ਚਿੰਤਾ ਅਤੇ ਅਸੁਰੱਖਿਆ ਦੇ ਹੇਠ ਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੇ ਹੋਰ ਵੀ ਕਾਰਨ ਹਨ ਜਿਵੇਂ ਕਿ ਆਪਣੇ ਆਪ ਵਿਚ ਰਹਿਣਾ, ਆਤਮਵਿਸ਼ਵਾਸ ਦੀ ਕਮੀ ਅਤੇ ਬੁਰੇ ਰਿਸ਼ਤੇ ਆਦਿ ।

(ਇ) ਰਸਾਇਣਿਕ ਤੱਤ (Chemical Factor) – ਕਈ ਅਪਾਹਜਤਾਵਾਂ ਰਸਾਇਣਿਕ ਪ੍ਰਦੂਸ਼ਣ ਨਾਲ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਰਸਾਇਣਿਕ ਪ੍ਰਦੂਸ਼ਣ, ਜਿਵੇਂ ਕਿ ਕਾਰਬਨ ਡਾਈਆਕਸਾਈਡ ਵਰਗੀਆਂ ਜ਼ਹਿਰੀਲੀਆਂ ਗੈਸਾਂ ਨਾਲ ਫੈਲਦਾ ਹੈ । ਇਸ ਨਾਲ ਲਗਾਤਾਰ ਸਿਰ ਦਰਦ ਅਤੇ ਸਾਹ ਰੁਕਣਾ ਆਦਿ ਬਿਮਾਰੀਆਂ ਲੱਗ ਸਕਦੀਆਂ ਹਨ । ਇਹ ਜ਼ਿਆਦਾਤਰ ਖਾਣਾਂ ਵਿਚ ਵਾਪਰਦਾ ਹੈ । ਹੋਰ ਜ਼ਹਿਰੀਲੀਆਂ ਗੈਸਾਂ ਜਿਵੇਂ ਕਾਰਬਨਡਾਈਆਕਸਾਈਡ, ਸਲਫਰਡਾਈਆਕਸਾਈਡ ਅਤੇ ਕਾਰਬਨ ਬਾਈਸਲਫਾਈਡ ਆਦਿ । ਇਹ ਗੈਸਾਂ ਕੰਮ ਕਰਨ ਵਾਲਿਆਂ ਦੁਆਰਾ ਸਾਹ ਲੈਣ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚੋਂ ਜਾ ਕੇ ਪਾਚਨ ਕ੍ਰਿਆ ਵਿਚ ਦਾਖਿਲ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਸਥਾਈ ਅਪੰਗਤਾ ਨੂੰ ਜਨਮ ਦਿੰਦੀਆਂ ਹਨ ।

(ਸ) ਮਾਨਸਿਕ ਕਾਰਕ (Psychological Factor) – ਕਈ ਕਿੱਤਾ ਸੰਬੰਧਿਤ ਕੰਮਾਂ ਦੇ ਵਾਤਾਵਰਣ ਵਿਚ ਮਾਨਸਿਕ ਅਸਮਰਥਤਾ ਦਾ ਜਨਮ ਹੁੰਦਾ ਹੈ । ਕਈ ਵਾਰ ਕੰਮ ਵਿਚ ਦਿਲ ਨਾ ਲੱਗਣਾ, ਨੌਕਰੀ ਤੋਂ ਖੁਸ਼ੀ ਨਾ ਮਿਲਣਾ, ਪਰਿਵਾਰਕ ਸਮੱਸਿਆਵਾਂ ਆਦਿ ਮਾਨਸਿਕ ਤਨਾਅ ਅਤੇ ਹੀਨਭਾਵਨਾ ਨੂੰ ਜਨਮ ਦਿੰਦੀ ਹੈ । ਇਹ ਤਨਾਅ ਕਈ ਵਾਰ ਕਿੱਤਾ ਸੰਬੰਧੀ ਕਿਸੇ ਦੁਰਘਟਨਾ ਕਾਰਨ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ।

(ਹ) ਮਕੈਨੀਕਲ ਕਾਰਕ (Mechanical Factor) – ਜ਼ਿਆਦਾਤਰ ਉਦਯੋਗਾਂ ਵਿਚ ਮਕੈਨੀਕਲ ਪ੍ਰੋਸੈਸਰ ਜੋ ਕਿ ਉਤਪਾਦਨ ਵਧਾਉਣ ਲਈ ਵਰਤੇ ਜਾਂਦੇ ਹਨ । ਮਸ਼ੀਨ ਕਾਰਨ ਦੁਰਘਟਨਾਵਾਂ ਦਾ ਕਾਰਨ ਬਣਦੇ ਹਨ । ਜੇਕਰ ਕੰਮ ਕਰਤਾ ਇਸਨੂੰ ਵਰਤ ਰਿਹਾ ਹੋਵੇ ਅਤੇ ਉਸ ਨੂੰ ਮਸ਼ੀਨੀ ਗਿਆਨ ਦੀ ਘਾਟ ਹੋਵੇ, ਇਹ ਉਸਨੂੰ ਮੁਸੀਬਤ ਵਿਚ ਪਾ ਸਕਦੀ ਹੈ । ਸੁਰੱਖਿਆ ਉਪਕਰਨਾਂ ਦੀ ਘਾਟ ਕਾਰਨ ਵੀ ਵੱਖ-ਵੱਖ ਮਕੈਨੀਕਲ ਘਟਨਾਵਾਂ ਦਾ ਖਤਰਾ ਵੱਧ ਜਾਂਦਾ ਹੈ । ਖੇਤੀਬਾੜੀ ਦੇ ਖੇਤਰ ਵਿਚ ਕਈ ਵਾਰ ਕਣਕ ਦੇ ਝਾੜਣ ਲਈ ਜੋ ਫ੍ਰੈਸ਼ਰ ਵਰਤੇ ਜਾਂਦੇ ਹਨ ਉਹਨਾਂ ਵਿਚ ਬਾਂਹਾਂ ਜਾਂ ਹੋਰ ਅੰਗ ਕੱਟੇ ਜਾਂਦੇ ਹਨ, ਜੋ ਮਕੈਨੀਕਲ ਲਾਪਰਵਾਹੀ ਦੇ ਕਾਰਨ ਹੁੰਦੇ ਹਨ ।

(ਕ) ਬਿਜਲੀ ਕਾਰਕ (Electrical Factor) – ਵੱਖ-ਵੱਖ ਫੈਕਟਰੀਆਂ ਵਿਚ ਵਰਤੇ ਜਾਣ ਵਾਲੇ ਬਿਜਲੀ ਯੰਤਰ ਨਾਲ ਇਲੈਕਟਿਕ ਸ਼ਾਟ ਹੋ ਸਕਦਾ ਹੈ ਅਤੇ ਇਹ ਮੌਤ ਦਾ ਕਾਰਨ ਬਣ ਜਾਂਦੀ ਹੈ । ਇਹ ਜ਼ਿਆਦਾਤਰ ਦੁਰਘਟਨਾਵਾਂ ਉਹਨਾਂ ਕਰਮਚਾਰੀਆਂ ਨਾਲ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਸੁਰੱਖਿਆ ਉਪਕਰਣ ਜਿਵੇਂ ਕਿ ਦਸਤਾਨੇ, ਹੈਲਮਟ, ਔਜ਼ਾਰਾਂ ਆਦਿ
ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕਰਦੇ । ਬਿਜਲੀ ਦੁਰਘਟਨਾਵਾਂ ਨੰਗੀਆਂ ਤਾਰਾਂ ਨੂੰ ਛੂਹਣ ਕਰਕੇ ਵੀ ਹੋ ਸਕਦੀਆਂ ਹਨ ।

4. ਦੁਰਘਟਨਾਵਾਂ (Accidents) – ਡਬਲਯੂ. ਐਚ. ਓ. ਦੇ ਅਨੁਸਾਰ (According to WHO), ਦੁਰਘਟਨਾ ਅਜਿਹੀ ਖੁੱਲ੍ਹੀ ਘਟਨਾ ਹੈ ਜੋ ਮਨੁੱਖ ਦੀ ਮਰਜ਼ੀ ਦੇ ਵਿਰੁੱਧ ਕਿਸੇ ਬਾਹਰਲੇ ਬਲ ਦੀ ਅਚਨਚੇਤੀ ਕ੍ਰਿਆ ਨਾਲ ਵਾਪਰਦੀ ਹੈ ਜਿਸ ਨਾਲ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਸੱਟਾਂ ਲੱਗਦੀਆਂ ਹਨ। ਬਿਨਾਂ ਸ਼ੋਰ ਦੁਰਘਟਨਾਵਾਂ ਵੱਧਦੀਆਂ ਜਾ ਰਹੀਆਂ ਹਨ । ਇਹ ਦੁਰਘਟਨਾਵਾਂ ਜਿਵੇਂ ਕਿ ਸੜਕ ਦੁਰਘਟਨਾ, ਘਰੇਲੂ ਦੁਰਘਟਨਾ ਅਤੇ ਕਿੱਤਾਕਾਰੀ ਦੁਰਘਟਨਾ ਆਦਿ ਹਨ ।

5. ਖੁਰਾਕੀ ਤੱਤ (Dietic Factors) – ਕੁਪੋਸ਼ਣ ਦਾ ਸਭ ਤੋਂ ਆਮ ਤਰੀਕਾ ਭੋਜਨ ਦਾ ਅਪੂਰਨ ਜਾਂ ਆਯੋਗ ਹੋਣਾ । ਕੁਪੋਸ਼ਣ ਕਾਰਨ ਅਨੀਮੀਆ ਭਾਵ ਖੂਨ ਦੀ ਕਮੀ ਹੁੰਦੀ ਹੈ । ਇਹ ਭੋਜਨ ਵਿਚ ਵਿਟਾਮਿਨਾਂ, ਕੈਲਸ਼ੀਅਮ ਜਾਂ ਫਾਰਫੋਰਸ ਨਮਕ ਜਾਂ ਧੁੱਪ ਦੇ ਕਾਰਨ ਹੁੰਦਾ ਹੈ ।

6. ਨਸ਼ਿਆਂ ਦੀ ਆਦਤ (Drug Addiction) – ਡਬਲਯੂ. ਐੱਚ. ਓ. (WHO) ਦੇ ਅਨੁਸਾਰ ਨਸ਼ੇ ਦੀ ਬੁਰਾਈ ਦਾ ਅਰਥ ਹੈ ਬਿਨਾਂ ਕਿਸੇ ਡਾਕਟਰੀ ਸਲਾਹ ਤੋਂ ਬਹੁ-ਮਾਤਰਾ ਵਿਚ ਕਿਸੇ ਰਸਾਇਣ ਦਾ ਵਾਰ-ਵਾਰ ਥੈ-ਸੇਵਨ ਕਰਨਾ ਜਿਸ ਵਿਚ ਵਿਅਕਤੀ ਵਿਚ ਆਮ ਕੰਮ ਕਰਨ ਦੀ ਯੋਗਤਾ ਦਾ ਨੁਕਸਾਨ ਹੁੰਦਾ ਹੈ । ਇਸ ਨਾਲ ਸਮਾਜਿਕ ਸਰੀਰਕ ਅਤੇ ਭਾਵਨਾਤਮਿਕ ਤੌਰ ਤੇ ਵੀ ਵਿਅਕਤੀ ਦਾ ਨੁਕਸਾਨ ਹੁੰਦਾ ਹੈ । ਨਸ਼ੇ ਵਿਸ਼ੇਸ਼ ਤੌਰ ਤੇ ਦਿਮਾਗ ਦੀ ਕਾਰਜਕੁਸ਼ਲਤਾ ਨੂੰ ਨਸ਼ਟ ਕਰ ਦਿੰਦੇ ਹਨ । ਬਹੁਤ ਸਾਰੇ ਦੇਸ਼ਾਂ ਵਿਚ ਨਸ਼ਾ ਇਕ ਚਿੰਤਾ ਦਾ ਕਾਰਨ ਬਣ ਗਿਆ ਹੈ । ਨਸ਼ੀਲੇ ਪਦਾਰਥ ਜਿਵੇਂ ਕਿ ਕੋਕੀਨ, ਹੇਰੋਇਨ, ਐੱਲ. ਐੱਸ. ਡੀ. (LSD) ਅਤੇ ਅਲਕੋਹਲ ਵਿਅਕਤੀ ਦੇ ਨਿਊਰੋਮਸਕੁਲਰ
ਤਾਲਮੇਲ ਨੂੰ ਖਰਾਬ ਕਰ ਦਿੰਦਾ ਹੈ ਜੋ ਕਿ ਅਸਮਰਥਾ ਦਾ ਕਾਰਨ ਬਣਦਾ ਹੈ ।

7. ਸਿੱਖਿਆ ਦੀ ਘਾਟ (Lack of Education – ਬਿਮਾਰੀ ਨੂੰ ਰੋਕਣ ਦੇ ਪ੍ਰਤੀ ਅਗਿਆਨਤਾ, ਆਮ ਤੌਰ ਤੇ ਮਾੜੀ ਸਫ਼ਾਈ, ਖੁਰਾਕ ਦੀ ਘਾਟ, ਅਣਸੁਰੱਖਿਆ ਸੰਭੋਗ (ਸਰੀਰਕ ਸੰਬੰਧ) ਅਤੇ ਟੀਕੇ ਆਦਿ ਲਗਾਉਣ ਬਾਰੇ ਅਨਪੜ੍ਹਤਾ ਦਾ ਕਾਰਨ ਹਨ । ਬਿਮਾਰੀ ਤੋਂ ਬਚਾਉ ਅਤੇ ਇਲਾਜ ਦਾ ਗਿਆਨ ਅਕਸਰ ਅਸਮਰਥਾ ਤੋਂ ਬਚਣ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ । ਕੰਮ ਸਮੇਂ ਅਸਮਰਥਤਾ ਸਿੱਖਿਆ ਦੀ ਘਾਟ ਵਜੋਂ ਵਾਪਰਦੀ ਹੈ । ਉਦਾਹਰਨ ਵਜੋਂ ਕਾਮਿਆਂ ਦੀ ਰੱਖਿਆ ਸੰਬੰਧੀ ਉਪਕਰਣਾਂ ਦੀ ਵਰਤੋਂ ਦੇ ਗਿਆਨ ਦੀ ਘਾਟ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 3.
ਪੇਸ਼ੇਵਰ ਬਿਮਾਰੀਆਂ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਆਕੂਪੇਸ਼ਨਲ ਸੇਫਟੀ ਐਂਡ ਹੈਲਥ ਕੰਨਵੈਨਸ਼ਨ (Occupational safety and health Convention) ਦੇ ਅਨੁਸਾਰ ਕਿੱਤਾ ਬਿਮਾਰੀ’’ ਪੇਸ਼ਾਵਰ ਬਿਮਾਰੀ ਸ਼ਬਦ ਉਹਨਾਂ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਨੂੰ ਕਵਰ ਕਰਦਾ ਹੈ ਜੋ ਕਿ ਕੰਮ ਦੀਆਂ ਗਤੀਵਿਧੀਆਂ ਤੋਂ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਜ਼ਖ਼ਮਾਂ ਦੇ ਐਕਸਪੋਜਰ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਆਉਂਦੇ ਹਨ । ਕਿੱਤਾ ਸੰਬੰਧੀ ਬਹੁਤ ਅਤੇ ਭਿੰਨ-ਭਿੰਨ ਬਿਮਾਰੀਆਂ ਹਨ ਜੋ ਕਿ ਵੱਖ-ਵੱਖ ਰੋਜ਼ਗਾਰ ਕੰਮਾਂ ਵਿਚੋਂ ਘਟਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚੋਂ ਕੁੱਝ ਬਿਮਾਰੀਆਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਦੱਸਿਆ ਗਿਆ ਹੈ-

ਭੌਤਿਕ ਕਾਰਨਾਂ ਕਰਕੇ ਪੈਦਾ ਹੋਏ ਰੋਗ (Diseases due to Physical agents)
ਧੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Dust Diseases or Dust hazard) .
ਰਸਾਇਣਿਕ ਤੱਤਾਂ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Chemical diseases or chemical hazards)
ਅਸਧਾਰਨ ਸਮੇਂ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਪੈਦਾ ਹੋਏ ਰੋਗ ।

ਇਹਨਾਂ ਉਪਰੋਕਤ ਤੱਤਾਂ ਤੋਂ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਰੋਗਾਂ ਬਾਰੇ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਵਿਸਥਾਰ ਵਿੱਚ ਦੱਸਿਆ ਗਿਆ ਹੈ ।

1. ਭੌਤਿਕ ਕਾਰਣਾਂ ਕਰਕੇ ਪੈਦਾ ਹੋਏ ਰੋਗ (Diseases due to Physical Agents) – ਇਸ ਸ਼੍ਰੇਣੀ ਵਿਚ ਉਹ ਬਿਮਾਰੀਆਂ ਆਉਂਦੀਆਂ ਹਨ ਜੋ ਕੰਮ ਕਰਨ ਵਾਲੇ ਸਥਾਨ ਤੋਂ ਉੱਚੇ ਅਤੇ ਨੀਵੇਂ ਤਾਪਮਾਨ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਬਹੁਤ ਉਦਯੋਗਿਕ ਕਰਮਚਾਰੀ ਜੋ ਕਿ ਬਹੁਤ ਹੀ ਗਰਮ ਤਾਪਮਾਨ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਕੋਲੇ ਦੀਆਂ ਖਾਣਾਂ ਦੇ ਭੱਠੇ ਆਦਿ ਵਿਚ ਚਿਹਰੇ ਦਾ ਜਲਣਾ, ਕੈਮਪ ਜਾਂ ਥਕਾਵਟ ਆਦਿ ਬਿਮਾਰੀਆਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ਅਤੇ ਜੋ ਉਦਯੋਗਿਕ ਕਰਮਚਾਰੀ ਬਹੁਤ ਹੀ ਠੰਡੇ ਤਾਪਮਾਨ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਫੋਰਸਟ ਬਾਈਟ, ਪੈਰਾਂ ਦਾ ਗਲਣਾ ਆਦਿ ਸਮੱਸਿਆਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਇਹਨਾਂ ਤੋਂ ਇਲਾਵਾ ਕੁਝ ਹੋਰ
ਵੀ ਭੌਤਿਕ ਕਾਰਕ ਹਨ ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

(ਉ) ਰੋਸ਼ਨੀ (Light – ਤੇਜ਼ ਰੋਸ਼ਨੀ ਜਾਂ ਘੱਟ ਰੋਸ਼ਨੀ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਅੱਖਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । ਜਿੱਥੇ ਤੇਜ਼ ਰੋਸ਼ਨੀ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਮਾਨਸਿਕ ਥਕਾਵਟ ਹੁੰਦੀ ਹੈ ਉੱਥੇ ਹੀ ਘੱਟ ਰੋਸ਼ਨੀ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਸਿਰ ਦਰਦ, ਅੱਖਾਂ ਤੇ ਭਾਰੀਪਨ ਅਤੇ ਮਾਨਸਿਕ ਦਬਾਅ ਵਰਗੀਆਂ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ ।

(ਈ) ਰੇਡੀਏਸ਼ਨ (Radiation) – ਵਿਕਿਰਣਾਂ ਨਾਲ ਆਦਰਾਂ ਦੇ ਤੱਲ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਦਾ ਹੈ ਜਿਸ ਨਾਲ ਉਲਟੀਆਂ, ਖੂਨ ਦੀ ਉਲਟੀਆਂ ਅਤੇ ਦਸਤ ਲੱਗ ਜਾਂਦੇ ਹਨ । ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਰੇਡੀਏਸ਼ਨ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਕੈਂਸਰ ਅਤੇ ਕਾਰਡੀਉਵੈਸਕੂਲਰ ਨਾਮਕ ਬਿਮਾਰੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

2. ਧੂੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Dust Diseases) – ਫੇਫੜਿਆਂ ਦੀਆਂ ਅਜਿਹੀਆਂ ਕਈ ਬਿਮਾਰੀਆਂ ਹਨ ਜੋ ਧੂੜ ਦੇ | ਸਰੀਰ ਵਿਚ ਜਾਣ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ | ਧੂੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਕੁਝ ਕੁ ਰੋਗ ਹੇਠ ਲਿਖੇ ਹਨ-

(ਉ) ਕੋਲੇ ਦੀ ਧੂੜ (Coal Dust-ਕਾਲੇ ਫੇਫੜਿਆਂ ਦੀ ਬਿਮਾਰੀ ਕੋਲੇ ਨੂੰ ਸਾਹ ਦੁਆਰਾ ਅੰਦਰ ਲੈ ਜਾਣ ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚ ਜਲਣ ਅਤੇ ਸੋਜ ਹੁੰਦੀ ਹੈ । ਇਹ ਇਕ ਸਥਾਈ ਬਿਮਾਰੀ ਹੁੰਦੀ ਹੈ ਜੋ ਫੇਫੜਿਆਂ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਂਦੀ ਹੈ ਅਤੇ ਸਾਹ ਲੈਣ ਵਿਚ ਮੁਸ਼ਕਿਲ ਪੈਦਾ ਕਰਦੀ ਹੈ ।

(ਅ) ਸਿਲਿਕਾ ਧੂੜ (Silica Dust) – ਇਹ ਸਥਿਤੀ ਉਦੋਂ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਸਿਲਿਕਾ ਕ੍ਰਿਸਟਲ ਖਾਣਾਂ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹੋਏ ਸਾਹ ਦੁਆਰਾ ਸਰੀਰ ਵਿਚ ਪਹੁੰਚਦੇ ਹਨ । ਇਸ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚ ਜਲਣ ਹੁੰਦੀ ਹੈ ਅਤੇ ਹੋਰ ਵੀ ਕਈ ਫੇਫੜਿਆਂ ਸੰਬੰਧੀ ਰੋਗ ਪੈਦਾ ਹੋ ਜਾਂਦੇ ਹਨ ।

(ਈ) ਕਪਾਹ ਦੀ ਧੂੜ/ਬਿਨੋਸਿਸ (Cotton dust/Byssinosis) – ਇਸਨੂੰ ਭੂਰਾ ਫੇਫੜਾ (Brown lung) ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਹ ਉਦੋਂ ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਕਰਮਚਾਰੀ ਭੰਗ, ਗੁਣ ਅਤੇ ਕਪਾਹ ਦੀ ਪਸੋਸਿੰਗ ਦੇ ਕੰਮ ਦੇ ਦੁਆਰਾ ਧੂੜ ਨੂੰ ਸਾਹ ਦੁਆਰਾ ਸਰੀਰ ਦੇ ਅੰਦਰ ਲੈਂਦਾ ਹੈ । ਇਹ ਇਕ ਭਿਅੰਕਰ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਛਾਤੀ ਤੰਗ ਜਾਂ ਜਕੜ ਜਾਂਦੀ ਹੈ ਅਤੇ ਸਾਹ ਦੀ ਕਮੀ ਹੋਣ ਲੱਗਦੀ ਹੈ । ਇਹ ਮੁੱਖ ਕਰਕੇ ਟੈਕਸਟਾਈਲ ਦੀਆਂ ਫੈਕਟਰੀਆਂ ਵਿਚ ਕੱਪੜਿਆਂ ਦਾ ਕੰਮ-ਕਾਜ ਕਰਦੇ ਨੂੰ ਹੁੰਦੀ ਹੈ ।

3. ਰਸਾਇਣਿਕ ਕਾਰਨਾਂ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Chemical Diseases) – ਸਾਡੀ ਰੋਜ਼ਾਨਾ ਦੀ ਜ਼ਿੰਦਗੀ ਅਤੇ ਉਦਯੋਗਾਂ ਵਿਚ ਵਿਆਪਕ ਤੌਰ ਤੇ ਰਸਾਇਣ ਵਰਤੇ ਜਾਂਦੇ ਹਨ । ਕਈ ਕੰਮਾਂ ਵਿਚ ਆਉਣ ਵਾਲੇ ਉਤਪਾਦ ਰਸਾਇਣਾਂ ਤੋਂ ਬਣਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਪਲਾਸਟਿਕ, ਪੇਂਟਸ, ਫਾਰਮੇਟਿਕਲ, ਡਿਟਰਜੈਂਟ ਆਦਿ । ਕਈ ਰਸਾਇਣਾਂ ਦਾ ਅਸਰ ਲੰਬੇ ਸਮੇਂ ਦੇ ਇਸਤੇਮਾਲ ਤੋਂ ਬਾਅਦ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ । ਇਸ ਵਿਚ ਡਾਇਬਟੀਜ਼, ਐਲਰਜੀ, ਦਮਾ, ਐਕਜ਼ੀਮਾ, ਕੈਂਸਰ, ਧਿਆਨ ਦੀ ਕਮੀ, ਸਿੱਖਣ ਵਿਚ ਕਮੀ, ਬਾਂਝਪਨ, ਡਿਪਰੈਸ਼ਨ, ਗੰਭੀਰ ਥਕਾਵਟ, ਰਸਾਇਣਿਕ ਸੰਵੇਦਨਸ਼ੀਲਤਾ, ਦਿਲ ਦੀ ਬਿਮਾਰੀ, ਮਲਟੀਪਲ ਸਕਲਰੋਸਿਸ, ਪਾਰਕਿੰਸਨਾਸ ਦੀ ਬਿਮਾਰੀ, ਥਾਈਰੋਡ ਬਿਮਾਰੀ ਆਦਿ ਰਸਾਇਣਿਕ ਤੱਤਾਂ ਤੋਂ ਹੋਣ ਵਾਲੀਆਂ ਬਿਮਾਰੀਆਂ ਹਨ | ਇਸ ਤੋਂ ਇਲਾਵਾ ਕੁਝ ਹੋਰ ਬਿਮਾਰੀਆਂ ਵੀ ਹਨ ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

(ਉ) ਜ਼ਹਿਰੀਲੀਆਂ ਗੈਸਾਂ ਨੂੰ ਸੁੰਘਣ ਨਾਲ ਹੋਣ ਵਾਲੀਆਂ ਬਿਮਾਰੀਆਂ-ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਗੈਸਾਂ ਜਿਵੇਂ ਕਿ ਕਲੋਰੀਨ (Chlorine), ਫਾਸਨ (Phosgene), ਸਲਫਰਡਾਈਆਕਸਾਈਡ (Sulphurdioxide), ਹਾਈਡਰੋਜਨ, ਗਿਲਫਾਇਡ, ਨਾਈਟ੍ਰੋਜਨ ਡਾਈਆਕਸਾਈਡ ਅਤੇ ਅਮੋਨੀਆ ਆਦਿ । ਜੇਕਰ ਅਚਾਨਕ ਉਦਯੋਗਿਕ ਹਾਦਸੇ ਵਿਚ ਲੀਕ ਹੋ ਜਾਵੇ ਤਾਂ ਇਹ ਬੁਰੀ ਤਰ੍ਹਾਂ ਫੇਫੜਿਆਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਜਿਵੇਂ ਕਿ ਕਲੋਰੀਨ ਅਤੇ ਅਮੋਨੀਆ ਨਾਮਕ ਗੈਸਾਂ ਆਸਾਨੀ ਨਾਲ ਸਰੀਰ ਅੰਦਰ ਦਾਖਿਲ ਹੋ ਕੇ ਮੂਹ, ਨੱਕ ਅਤੇ ਗਲੇ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀਆਂ ਹਨ ।

(ਅ) ਲੀਡ ਜ਼ਹਿਰ (Lead Poisoning) – ਲੀਡ ਜ਼ਹਿਰ ਦੇ ਛੋਟੇ-ਛੋਟੇ ਕਣਾਂ ਦੇ ਸਰੀਰ ਵਿਚ ਜਾਣ ਨਾਲ ਇਕ ਕਰਮਚਾਰੀ ਨੂੰ ਪੇਟ ਦੀ ਕਬਜ਼ੀ, ਅਨੀਮੀਆ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਵਿਚ ਦਰਦ ਹੋ ਸਕਦਾ ਹੈ ।

4. ਅਸਧਾਰਨ ਸਮੇਂ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਰੋਗ (Diseases due to unusual timings of the Workers) – ਅੱਜ ਦੇ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਵਿਚ ਸੰਸਾਰ ਵਿਚ ਤਕਨੀਕੀ ਵਿਕਾਸ ਹੋ ਰਿਹਾ ਹੈ । ਇਹ ਵੀ ਨੋਟਿਸ ਕੀਤਾ ਗਿਆ ਹੈ ਕਿ ਤਕਨੀਕੀ ਕੰਪਨੀਆਂ ਨੌਕਰੀ ਵੀ ਮੁਹੱਈਆ ਕਰਵਾ ਰਹੀਆਂ ਹਨ । ਇਹ ਕੰਪਨੀਆਂ ਭਾਰਤ ਵਿਚ ਵੀ ਨੌਕਰੀਆਂ ਮੁਹੱਈਆ ਕਰਵਾ ਰਹੀਆਂ ਹਨ, ਪਰ ਦਿਨ-ਰਾਤ ਦੇ ਅੰਤਰ ਵਜੋਂ ਕਰਮਚਾਰੀਆਂ ਨੂੰ ਰਾਤ ਨੂੰ ਜਾਂ ਫਿਰ ਸ਼ਾਮ ਦੀ ਸਿਫਟ ਵਿਚ ਕੰਮ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਉਹਨਾਂ ਨੂੰ ਜੀਵਨ-ਸ਼ੈਲੀ ਸੰਬੰਧਿਤ ਰੋਗਾਂ ਦਾ ਸ਼ਿਕਾਰ ਹੋਣਾ ਪੈ ਰਿਹਾ ਹੈ । ਇਹ ਰੋਗ ਜਿਵੇਂ ਕਿ ਡਾਇਬਟੀਜ਼, ਹਾਈ ਪ੍ਰੋਟੇਸ਼ਨ, ਇਨਸੋਮਨੀਆ ਨੀਂਦ ਨਾ ਆਉਣਾ) ਆਦਿ ਗਲਤ ਸਮੇਂ ਵਿਚ ਕੰਮ ਕਰਨ ਕਾਰਨ ਹੋ ਰਹੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਅਸਮਰਥਤਾ ਸ਼ਬਦ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਉ ਅਤੇ ਅਪਾਹਜਪੁਣੇ ਦੇ ਵੱਖ-ਵੱਖ ਪ੍ਰਭਾਵੀ ਉਪਾਵਾਂ ਬਾਰੇ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
ਅਸਮਰਥਤਾ ਦਾ ਅਰਥ ਹੈ, ਕੋਈ ਵਿਸ਼ੇਸ਼ ਸਰੀਰਕ ਜਾਂ ਮਾਨਸਿਕ ਕੰਮ ਕਰਨ ਦੀ ਅਯੋਗਤਾ ! ਜਦੋਂ | ਸਰੀਰਕ ਮਾਨਸਿਕ ਕਾਰਜ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਘੱਟ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇਸ ਅਵਸਥਾ ਨੂੰ ਅਸਮਰਥਤਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਡਬਲਯੂ. ਐੱਚ. ਓ. ਅਨੁਸਾਰ (W.H.0.), ਇਕ ਸਿਹਤਮੰਦ ਅਤੇ ਸਧਾਰਨ ਵਿਅਕਤੀ ਲਈ ਨਿਰਧਾਰਿਤ ਕੰਮ ਕਰਨ ਵਿਚ ਆਈ ਰੁਕਾਵਟ ਦੀ ਆਯੋਗਤਾ ਨੂੰ ਅਸਮਰਥਾ ਆਖਿਆ ਜਾਂਦਾ ਹੈ ।

ਅਸਮਰਥਤਾ ਦੇ ਵੱਖ-ਵੱਖ ਪ੍ਰਭਾਵੀ ਉਪਾਅ-
1. ਨੌਕਰੀ ਤੇ ਰੱਖਣ ਤੋਂ ਪਹਿਲਾਂ ਮੈਡੀਕਲ ਚੈੱਕਅਪ (Medical checkup before Joining) – ਇਸ ਚੈੱਕਅਪ ਦਾ ਉਦੇਸ਼ ਸਹੀ ਨੌਕਰੀ ਤੇ ਸਹੀ 9ਮੀ ਵ ਤੰਦਰੁਸਤ ਆਦਮੀ ਨੂੰ ਰੱਖਣਾ ਹੈ । ਇਕ ਸਹੀ ਵਿਅਕਤੀ ਨੂੰ ਉਦੋਂ ਹੀ ਨੌਕਰੀ ਦਿੱਤੀ ਜਾਣੀ ਚਾਹੀਰੀ ਵੇਰ ਉਰ ਡਾਕਟਰੀ ਤੌਰ ਤੇ ਫਿੱਟ ਹੋਵੇ ਤਾਂ ਕਿ ਉਹ ਬਿਨਾਂ ਕਿਸੇ ਖ਼ਤਰੇ ਤੋਂ ਆਪਣੇ ਕੰਮ ਨੂੰ ਕੁਸ਼ਲਤਾ ਪੂਰਵਕਾ ਕਰ ਕੇ ਜਿਵੇਂ ਕਿ ਜੇਕਰ ਕਿਸੇ ਨੂੰ ਦਮੇ ਦੀ ਸ਼ਿਕਾਇਤ ਹੈ ਤਾਂ ਉਸਨੂੰ ਕੋਲੇ ਦੀਆਂ ਖਾਣਾਂ (mines) ਵਿਚ ਨਹੀਂ ਹੱਲ ਰਾਹੀਲ ।

2. ਕਰਮਚਾਰੀਆਂ ਦੀ ਸਮੇਂ-ਸਮੇਂ ਤੇ ਸਿੱਖ ਹੋਣਾ (Periodical examination of Workers) – ਕਈ ਕਿੱਤਾ ਸੰਬੰਧੀ ਬਿਮਾਰੀਆਂ ਲਗਣ ਨੂੰ ਬਰਡ ਏਬਾ ਸਮਾਂ ਲੱਗਦਾ ਹੈ । ਇਹਨਾਂ ਬਿਮਾਰੀਆਂ ਨੂੰ ਸ਼ੁਰੂਆਤੀ ਪੜਾਅ ਵਿਚ ਪਛਾਣਨਾ ਮੁਸ਼ਕਿਲ ਹੁੰਦਾ ਹੈ | ਸਮੇਂ-ਸਮੇਂ ਤੇ ਜਾਂਚ ਕਰਨ ਨਾਲ ਸ਼ੁਰੂਆਤੀ ਪੜਾਅ ਵਿਚ ਬਿਮਾਰੀ ਪਛਾਣ ਕਰਕੇ ਉਸਨੂੰ ਅਸਾਨੀ ਅਤੇ ਤੇਜ਼ੀ ਨਾਲ ਠੀਕ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਸਮੇਂ ਤੇ ਜਾਂਚ ਕਰਨ ਦਾ ਮੁੱਖ ਉਦੇਸ਼ ਮੁਢਲੇ ਪੜਾਅ ਤੇ ਬਿਮਾਰੀ ਦਾ ਪਤਾ ਲਗਾਉਣਾ ਅਤੇ ਇਲਾਜ ਕਰਨਾ ਹੈ ।

3. ਕੰਮ ਕਰਨ ਦੇ ਸਥਾਨ ਦਾ ਰੱਖ-ਰਖਾਉ (Maintenance of working Place) – ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਭੌਤਿਕ ਏਜੰਟਾਂ ਦੇ ਕਾਰਨ ਜਿਵੇਂ ਗਰਮੀ ਸਰਦੀ, ਦਬਾਅ, ਰੇਡੀਏਸ਼ਨ, ਰੌਲਾ ਆਦਿ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਇਹਨਾਂ ਭੌਤਿਕ ਏਜੰਟਾਂ ਦੇ ਰੋ 1-ਰਖਾਵ ਵੱਲ ਖਾਸ ਧਿਆਨ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਕ ਮੁਆਇਨ ਕਰਤਾ ਨੂੰ ਠੰਡੇ, ਹਲਕੇ, ਹਵਾਦਾਰ ਤਾਪਮਾਨ ਅਤੇ ਨਮੀ ਦੀ ਜਾਂਚ ਅਤੇ ਸਾਂਭ-ਸੰਭਾਲ ਨੂੰ ਚੈੱਕ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਵਾਸਤੇ ਹੇਠ ਲਿਖੇ ਕਦਮ ਚੁੱਕੇ ਜਾਣੇ ਚਾਹੀਦੇ ਹਨ-

(ਉ) ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਤੇ ਰੋਕ (Control of air Pollution) – ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਕਾਰਨ ਹੁੰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਉਪਾਅ ਨਾਲ ਰੋਕਣਾ ਚਾਹੀਦਾ ਹੈ ।

(ਅ ਨਮੀ ਵਧਾ ਕੇ-ਧੂੜ ਨੂੰ ਨਮੀ ਨਾਲ ਘਟਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿਉਂਕਿ ਧੂੜ ਖੁਸ਼ਕ ਹਵਾ ਵਿਚ ਜ਼ਿਆਦਾ ਫੈਲਦੀ ਜਾਂ ਤੈਰਦੀ ਹੈ । ਕੰਮਕਾਜੀ ਸਥਾਨ ਤੇ ਪਾਣੀ ਦਾ ਛਿੜਕਾਅ ਕਰਕੇ, ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਨੂੰ ਕੰਟਰੋਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕਿਸੇ ਵੀ ਸਮੱਗਰੀ ਨੂੰ ਪੀਸਣ ਤੋਂ ਪਹਿਲਾਂ ਉਸ ਵਿਚ ਨਮੀ ਪੈਦਾ ਥੋੜ੍ਹਾ ਪਾਣੀ ਦਾ ਛਿੜਕਾਅ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਇਸ ਨਾਲ ਹਵਾ ਦਾ ਪ੍ਰਦੂਸ਼ਣ ਨਹੀਂ ਫੈਲਦਾ ।

(ਇ) ਅਲੱਗ ਨੱਥੀ ਕਰਨਾ (Seperate Enclosure)-ਫੈਕਟਰੀ ਵਿਚ ਹਾਨੀਕਾਰਕ ਸਮੱਗਰੀ ਨੂੰ ਵੱਖਰੇ ਤੌਰ ਤੇ ਨੱਥੀ | ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਭਾਵ ਇਹਨਾਂ ਕੈਮੀਕਲਾਂ ਨੂੰ ਅਲੱਗ ਥਾਂ ਤੇ ਬੰਦ ਕਰਕੇ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਕਿ ਇਹਨਾਂ ਦੀ ਧੂੜ ਫੈਕਟਰੀ ਵਿਚ ਨਾ ਫੈਲੇ ।

ਨਿਕਾਸ – ਫੈਕਟਰੀਆਂ ਵਿਚ ਵੈਂਟੀਲੇਸ਼ਨ ਦੀ ਵਿਵਸਥਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਤਾਂਕਿ ਫੈਕਟਰੀਆਂ ਦੀ ਧੂੜ ਦਾ ਧੂੰਆਂ ਅਤੇ ਸੁਗੰਧ ਆਦਿ ਬਾਹਰ ਕੱਢੇ ਜਾ ਸਕਣ ।

ਪ੍ਰਸ਼ਨ 5.
ਕੰਮ ਕਰਨ ਵਾਲੀ ਥਾਂ ਤੇ ਕਮਿਆਂ ਦੀ ਡਾਕਟਰੀ ਜਾਂਚ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਆਕੁਪੋਸਟਲ ਹੈਲਥ ਦਾ ਮੁੱਖ ਉਦੇਸ਼ ਹਰ ਤਰ੍ਹਾਂ ਦੇ ਕੰਮਾਂ ਵਿਚ ਲੱਗੇ ਕਰਮਚਾਰੀਆਂ ਵਰਕਰਾਂ ਦੀ ਸਿਹਤ ਦੀ ਸੰਭਾਲ ਅਤੇ ਸਿਹਤ ਦੇ ਸਤਰ ਨੂੰ ਉੱਚਾ ਚੁੱਕਣਾ ਹੈ | ਕਰਮਚਾਰੀਆਂ ਨੂੰ ਸਰੀਰਕ, ਮਾਨਸਿਕ ਅਤੇ ਜਜ਼ਬਾਤੀ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਰੱਖਣ ਲਈ ਕੁਝ ਪ੍ਰਤੀਰੋਧੀ ਢੰਗ ਅਪਣਾਏ ਜਾਂਦੇ ਹਨ ਜੋ ਕਿ ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਨੂੰ ਰੋਕਣ ਵਿਚ ਸਮਰੱਥ ਹੁੰਦੇ ਹਨ | ਵਿਵਸਾਇਕ ਵਾਤਾਵਰਣ ਵਿਚ ਬਹੁਤ ਸਾਰੀਆਂ ਅਸਮਰਥਾਵਾਂ ਵਾਪਰਦੀਆਂ ਹਨ | ਵਿਵਸਾਇਕ ਖਤਰਾ ਉਹਨਾਂ ਥਾਂਵਾਂ ਤੇ ਆਮ ਹੁੰਦਾ ਹੈ ਜਿੱਥੇ ਕਰਮਚਾਰੀ ਵਿਵਸਾਇਕ ਸੰਬੰਧੀ ਸਿਧਾਂਤਾਂ ਨੂੰ ਨਹੀਂ ਅਪਣਾਉਂਦੇ ਹਨ । ਰੋਜ਼ਗਾਰ ਵਿਚ ਵਿਵਸਾਇਕ ਖਤਰਿਆਂ ਨੂੰ ਘਟਾਉਣ ਲਈ ਹੇਠ ਲਿਖੇ ਨਿਵਾਰਕ ਢੰਗਾਂ ਦੀ ਪਾਲਣਾ ਕਰਨੀ ਚਾਹੀਦੀ
ਹੈ ।

1. ਨੌਕਰੀ ਤੇ ਰੱਖਣ ਤੋਂ ਪਹਿਲਾਂ ਮੈਡੀਕਲ ਚੈੱਕਅਪ (Medical checkup before Joining) – ਇਸ ਚੈੱਕਅਪ ਦਾ ਉਦੇਸ਼ ਸਹੀ ਨੌਕਰੀ ਤੇ ਸਹੀ ਆਦਮੀ ਭਾਵ ਤੰਦਰੁਸਤ ਆਦਮੀ ਨੂੰ ਰੱਖਣਾ ਹੈ । ਇਕ ਸਹੀ ਵਿਅਕਤੀ ਨੂੰ ਉਦੋਂ ਹੀ ਨੌਕਰੀ ਦਿੱਤੀ ਜਾਣੀ ਚਾਹੀਦੀ ਹੈ ਜਦ ਉਹ ਡਾਕਟਰੀ ਤੌਰ ਤੇ ਫਿੱਟ ਹੋਵੇ ਤਾਂ ਕਿ ਉਹ ਬਿਨਾਂ ਕਿਸੇ ਖ਼ਤਰੇ ਤੋਂ ਆਪਣੇ ਕੰਮ ਨੂੰ ਕੁਸ਼ਲਤਾ ਪੂਰਵਕ ਕਰ ਸਕੇ। ਜਿਵੇਂ ਕਿ ਜੇਕਰ ਕਿਸੇ ਨੂੰ ਦਮੇ ਦੀ ਸ਼ਿਕਾਇਤ ਹੈ ਤਾਂ ਉਸਨੂੰ ਕੋਲੇ ਦੀਆਂ ਖਾਣਾਂ (mines) ਵਿਚ ਨਹੀਂ ਰੱਖਣਾ ਚਾਹੀਦਾ ।

2. ਕਰਮਚਾਰੀਆਂ ਦੀ ਸਮੇਂ-ਸਮੇਂ ਤੇ ਜਾਂਚ ਹੋਣਾ (Periodical examination of Workers) – ਕਈ ਕਿੱਤਾ ਸੰਬੰਧੀ ਬਿਮਾਰੀਆਂ ਲਗਣ ਨੂੰ ਬਹੁਤ ਲੰਬਾ ਸਮਾਂ ਲੱਗਦਾ ਹੈ । ਇਹਨਾਂ ਬਿਮਾਰੀਆਂ ਨੂੰ ਸ਼ੁਰੂਆਤੀ ਪੜਾਅ ਵਿਚ ਪਛਾਣਨਾ ਮੁਸ਼ਕਿਲ ਹੁੰਦਾ ਹੈ । ਸਮੇਂ-ਸਮੇਂ ਤੇ ਜਾਂਚ ਕਰਨ ਨਾਲ ਸ਼ੁਰੂਆਤੀ ਪੜਾਅ ਵਿਚ ਬਿਮਾਰੀ ਪਛਾਣ ਕਰਕੇ ਉਸਨੂੰ ਅਸਾਨੀ ਅਤੇ ਤੇਜ਼ੀ ਨਾਲ ਠੀਕ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ | ਸਮੇਂ ਤੇ ਜਾਂਚ ਕਰਨ ਦਾ ਮੁੱਖ ਉਦੇਸ਼ ਮੁਢਲੇ ਪੜਾਅ ਤੇ ਬਿਮਾਰੀ ਦਾ ਪਤਾ ਲਗਾਉਣਾ ਅਤੇ ਇਲਾਜ ਕਰਨਾ ਹੈ ।

3. ਕੰਮ ਕਰਨ ਦੇ ਸਥਾਨ ਦਾ ਰੱਖ-ਰਖਾਉ (Maintenance of working Place) – ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਭੌਤਿਕ ਏਜੰਟਾਂ ਦੇ ਕਾਰਨ ਜਿਵੇਂ ਗਰਮੀ, ਸਰਦੀ, ਦਬਾਅ, ਰੇਡੀਏਸ਼ਨ, ਰੌਲਾ ਆਦਿ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਇਹਨਾਂ ਭੌਤਿਕ ਏਜੰਟਾਂ ਦੇ ਰੱਖ-ਰਖਾਵ ਵੱਲ ਖਾਸ ਧਿਆਨ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਕ ਮੁਆਇਨ ਕਰਤਾ ਨੂੰ ਠੰਡੇ, ਹਲਕੇ, ਹਵਾਦਾਰ ਤਾਪਮਾਨ ਅਤੇ ਨਮੀ ਦੀ ਜਾਂਚ ਅਤੇ ਸਾਂਭ-ਸੰਭਾਲ ਨੂੰ ਚੈੱਕ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਵਾਸਤੇ ਹੇਠ ਲਿਖੇ ਕਦਮ ਚੁੱਕੇ ਜਾਣੇ ਚਾਹੀਦੇ ਹਨ |

ਪ੍ਰਸ਼ਨ 6.
ਆਮ ਕਿੱਤਾ ਸੰਬੰਧੀ ਬਿਮਾਰੀਆਂ ਕਿਹੜੀਆਂ ਹਨ ? ਵਿਸਥਾਰ ਨਾਲ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
ਆਕੁਪੇਸ਼ਨਲ ਸੇਫਟੀ ਐਂਡ ਹੈਲਥ ਕੰਨਵੈਨਸ਼ਨ (Occupational safety and health Convention) ਦੇ ਅਨੁਸਾਰ “ਕਿੱਤਾ ਬਿਮਾਰੀ’ ਸ਼ਬਦ ਉਹਨਾਂ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਨੂੰ ਕਵਰ ਕਰਦਾ ਹੈ ਜੋ ਕਿ ਕੰਮ ਦੀਆਂ ਗਤੀਵਿਧੀਆਂ ਤੋਂ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਜ਼ਖ਼ਮਾਂ ਦੇ ਐਕਸਪੋਜਰ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਆਉਂਦੇ ਹਨ । ਕਿੱਤਾ ਸੰਬੰਧੀ ਬਹੁਤ ਅਤੇ ਭਿੰਨ-ਭਿੰਨ ਬਿਮਾਰੀਆਂ ਹਨ ਜੋ ਕਿ ਵੱਖ-ਵੱਖ ਰੋਜ਼ਗਾਰ ਕੰਮਾਂ ਵਿਚੋਂ ਘਟਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚੋਂ ਕੁੱਝ ਬਿਮਾਰੀਆਂ ਨੂੰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਦੱਸਿਆ ਗਿਆ ਹੈ-

ਭੌਤਿਕ ਕਾਰਨਾਂ ਕਰਕੇ ਪੈਦਾ ਹੋਏ ਰੋਗ (Diseases due to Physical agents)
ਧੂੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Dust Diseases or Dust hazard)
ਰਸਾਇਣਿਕ ਤੱਤਾਂ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Chemical diseases or chemical hazards)
ਅਸਧਾਰਨ ਸਮੇਂ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਪੈਦਾ ਹੋਏ ਰੋਗ ।

ਇਹਨਾਂ ਉਪਰੋਕਤ ਤੱਤਾਂ ਤੋਂ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਰੋਗਾਂ ਬਾਰੇ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਵਿਸਥਾਰ ਵਿੱਚ ਦੱਸਿਆ ਗਿਆ ਹੈ ।
1. ਭੌਤਿਕ ਕਾਰਣਾਂ ਕਰਕੇ ਪੈਦਾ ਹੋਏ ਰੋਗ (Diseases due to Physical Agents) – ਇਸ ਸ਼੍ਰੇਣੀ ਵਿਚ ਉਹ ਬਿਮਾਰੀਆਂ ਆਉਂਦੀਆਂ ਹਨ ਜੋ ਕੰਮ ਕਰਨ ਵਾਲੇ ਸਥਾਨ ਤੋਂ ਉੱਚੇ ਅਤੇ ਨੀਵੇਂ ਤਾਪਮਾਨ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ | ਬਹੁਤ ਉਦਯੋਗਿਕ ਕਰਮਚਾਰੀ ਜੋ ਕਿ ਬਹੁਤ ਹੀ ਗਰਮ ਤਾਪਮਾਨ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਕੋਲੇ ਦੀਆਂ ਖਾਣਾਂ ਦੇ ਭੱਠੇ ਆਦਿ ਵਿਚ ਚਿਹਰੇ ਦਾ ਜਲਣਾ, ਕੈਮਪੂ ਜਾਂ ਥਕਾਵਟ ਆਦਿ ਬਿਮਾਰੀਆਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ਅਤੇ ਜੋ ਉਦਯੋਗਿਕ ਕਰਮਚਾਰੀ ਬਹੁਤ ਹੀ ਠੰਡੇ ਤਾਪਮਾਨ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਫੋਰਸਟ ਬਾਈਟ, ਪੈਰਾਂ ਦਾ ਗਲਣਾ ਆਦਿ ਸਮੱਸਿਆਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਇਹਨਾਂ ਤੋਂ ਇਲਾਵਾ ਕੁਝ ਹੋਰ
ਵੀ ਭੌਤਿਕ ਕਾਰਕ ਹਨ ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

(ਈ) ਰੇਡੀਏਸ਼ਨ (Rediation) – ਵਿਕਿਰਣਾਂ ਨਾਲ ਆਦਰਾਂ ਦੇ ਤੱਲ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਦਾ ਹੈ ਜਿਸ ਨਾਲ ਉਲਟੀਆਂ, ਖ਼ੂਨ ਦੀ ਉਲਟੀਆਂ ਅਤੇ ਦਸਤ ਲੱਗ ਜਾਂਦੇ ਹਨ । ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਰੇਡੀਏਸ਼ਨ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਕੈਂਸਰ ਅਤੇ | ਕਾਰਡੀਉਵੈਸਕੁਲਰ ਨਾਮਕ ਬਿਮਾਰੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

2. ਧੂੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Dust Diseases) – ਫੇਫੜਿਆਂ ਦੀਆਂ ਅਜਿਹੀਆਂ ਕਈ ਬਿਮਾਰੀਆਂ ਹਨ ਜੋ ਧੂੜ ਦੇ ਸਰੀਰ ਵਿਚ ਜਾਣ ਕਰਕੇ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ | ਧੂੜ ਤੋਂ ਪੈਦਾ ਹੋਏ ਕੁਝ ਕੁ ਰੋਗ ਹੇਠ ਲਿਖੇ ਹਨ-

(ਉ) ਕੋਲੇ ਦੀ ਧੂੜ (Coal Dust) – ਕਾਲੇ ਫੇਫੜਿਆਂ ਦੀ ਬਿਮਾਰੀ ਕੋਲੇ ਨੂੰ ਸਾਹ ਦੁਆਰਾ ਅੰਦਰ ਲੈ ਜਾਣ ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚ ਜਲਣ ਅਤੇ ਸੋਜ ਹੁੰਦੀ ਹੈ । ਇਹ ਇਕ ਸਥਾਈ ਬਿਮਾਰੀ ਹੁੰਦੀ ਹੈ ਜੋ ਫੇਫੜਿਆਂ ਨੂੰ ਨੁਕਸਾਨ ਪਹੁੰਚਾਉਂਦੀ ਹੈ ਅਤੇ ਸਾਹ ਲੈਣ ਵਿਚ ਮੁਸ਼ਕਿਲ ਪੈਦਾ ਕਰਦੀ ਹੈ ।

(ਅ) ਸਿਲਿਕਾ ਧੂੜ (Silica Dust) – ਇਹ ਸਥਿਤੀ ਉਦੋਂ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ਜਦੋਂ ਸਿਲਿਕਾ ਟਿਲ ਖਾਂਣਾਂ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹੋਏ ਸਾਹ ਦੁਆਰਾ ਸਰੀਰ ਵਿਚ ਪਹੁੰਚਦੇ ਹਨ। ਇਸ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚ ਜਲਣ ਹੁੰਦੀ ਹੈ ਅਤੇ ਹੋਰ ਵੀ ਕਈ ਫੇਫੜਿਆਂ ਸੰਬੰਧੀ ਰੋਗ ਪੈਦਾ ਹੋ ਜਾਂਦੇ ਹਨ ।

(ਬ) ਕਪਾਹ ਦੀ ਧੂੜ/ਬਿਸੀਨੋਸਿਸ (Cotton dust/Byssinosis) – ਇਸਨੂੰ ਭੂਰਾ ਫੇਫੜਾ (Brown lung) ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਹ ਉਦੋਂ ਹੁੰਦਾ ਹੈ ਜਦੋਂ ਕਰਮਚਾਰੀ ਭੰਗ, ਗੁਣ ਅਤੇ ਕਪਾਹ ਦੀ ਸੋਸਿੰਗ ਦੇ ਕੰਮ ਦੇ ਦੁਆਰਾ, ਧੂੜ ਨੂੰ ਸਾਹ ਦੁਆਰਾ ਸਰੀਰ ਦੇ ਅੰਦਰ ਲੈਂਦਾ ਹੈ । ਇਹ ਇਕ ਭਿਅੰਕਰ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਛਾਤੀ ਤੰਗ ਜਾਂ ਜਕੜ ਜਾਂਦੀ ਹੈ ਅਤੇ ਸਾਹ ਦੀ ਕਮੀ ਹੋਣ ਲੱਗਦੀ ਹੈ । ਇਹ ਮੁੱਖ ਕਰਕੇ ਟੈਕਸਟਾਈਲ ਦੀਆਂ ਫੈਕਟਰੀਆਂ ਵਿਚ ਕੱਪੜਿਆਂ ਦਾ ਕੰਮ-ਕਾਜ ਕਰਦੇ ਹਨ ।

3. ਰਸਾਇਣਿਕ ਕਾਰਨਾਂ ਤੋਂ ਪੈਦਾ ਹੋਏ ਰੋਗ (Chemical Diseases) – ਸਾਡੀ ਰੋਜ਼ਾਨਾ ਦੀ ਜ਼ਿੰਦਗੀ ਅਤੇ ਉਦਯੋਗਾਂ ਵਿਚ ਵਿਆਪਕ ਤੌਰ ਤੇ ਰਸਾਇਣ ਵਰਤੇ ਜਾਂਦੇ ਹਨ ।ਕਈ ਕੰਮ ਵਿਚ ਆਉਣ ਵਾਲੇ ਉਤਪਾਦ ਰਸਾਇਣਾਂ ਤੋਂ ਬਣਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਪਲਾਸਟਿਕ, ਪੇਂਟਸ, ਫਾਰਮੇਟਿਕਲੇ, ਡਿਟਰਜੈਂਟ ਆਦਿ | ਕਈ ਰਸਾਇਣਾਂ ਦਾ ਅਸਰ ਲੰਬੇ ਸਮੇਂ ਦੇ ਇਸਤੇਮਾਲ ਤੋਂ ਬਾਅਦ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ । ਇਸ ਵਿਚ ਡਾਇਬਟੀਜ, ਐਲਰਜੀ, ਦਮਾ, ਐਕਜ਼ੀਮਾ, ਕੈਂਸਰ, ਧਿਆਨ ਦੀ ਕਮੀ, ਸਿੱਖਣ ਵਿਚ ਕਮੀ, ਬਾਂਝਪਨ, ਡਿਪਰੈਸ਼ਨ, ਗੰਭੀਰ ਥਕਾਵਟ, ਰਸਾਇਣਿਕ ਸੰਵੇਦਨਸ਼ੀਲਤਾ, ਦਿਲ ਦੀ ਬਿਮਾਰੀ, ਮਲਟੀਪਲ ਸਕਲਰੋਸਿਸ, ਪਾਰਕਿੰਸਨਾਸ ਦੀ ਬਿਮਾਰੀ, ਥਾਈਰੋਡ ਬਿਮਾਰੀ ਆਦਿ ਰਸਾਇਣਿਕ ਤੱਤਾਂ ਤੋਂ ਹੋਣ ਵਾਲੀਆਂ ਬਿਮਾਰੀਆਂ ਹਨ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕੁਝ ਹੋਰ ਬਿਮਾਰੀਆਂ ਵੀ ਹਨ ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

(ਉ) ਜ਼ਹਿਰੀਲੀਆਂ ਗੈਸਾਂ ਨੂੰ ਸੁੰਘਣ ਨਾਲ ਹੋਣ ਵਾਲੀਆਂ ਬਿਮਾਰੀਆਂ – ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਗੈਸਾਂ ਜਿਵੇਂ ਕਿ ਕਲੋਰੀਨ (chlorine), ਫਾਸਗਿਨ (Phosgene), ਸਲਫਰਡਾਈਆਕਸਾਈਡ (Sulphurdioxide), ਹਾਈਡਰੋਜਨ, ਗਿਲਫਾਇਡ, ਨਾਈਟ੍ਰੋਜਨ ਡਾਈਆਕਸਾਈਡ ਅਤੇ ਅਮੋਨੀਆ ਆਦਿ । ਜੇਕਰ ਅਚਾਨਕ ਉਦਯੋਗਿਕ ਹਾਦਸੇ ਵਿਚ ਲੀਕ ਹੋ ਜਾਵੇ ਤਾਂ ਇਹ ਬੁਰੀ ਤਰ੍ਹਾਂ ਫੇਫੜਿਆਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਜਿਵੇਂ ਕਿ ਕਲੋਰੀਨ ਅਤੇ ਅਮੋਨੀਆ ਨਾਮਕ ਗੈਸਾਂ ਆਸਾਨੀ ਨਾਲ ਸਰੀਰ ਅੰਦਰ ਦਾਖਿਲ ਹੋ ਕੇ ਮੂੰਹ, ਨੱਕ ਅਤੇ ਗਲੇ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀਆਂ ਹਨ ।

(ਅ) ਲੀਡ ਜ਼ਹਿਰ (Lead Poisoning) – ਲੀਡ ਜ਼ਹਿਰ ਦੇ ਛੋਟੇ-ਛੋਟੇ ਕਣਾਂ ਦੇ ਸਰੀਰ ਵਿਚ ਜਾਣ ਨਾਲ, ਇਕ ਕਰਮਚਾਰੀ ਨੂੰ ਪੇਟ ਦੀ ਕਬਜ਼ੀ, ਅਨੀਮੀਆ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਵਿਚ ਦਰਦ ਹੋ ਸਕਦਾ ਹੈ । (ਈ ਮਰਕਿਊਰੀ ਜ਼ਹਿਰ (Mercury Poisoning-ਮਰਕਿਊਰੀ ਜ਼ਹਿਰ ਦੇ ਸਰੀਰ ਵਿਚ ਦਾਖਲ ਹੋਣ ਨਾਲ ਸਾਹ ਲੈਣ ਵਿਚ ਤਕਲੀਫ, ਮਸੂੜਿਆਂ ਵਿਚ ਸੋਜ਼, ਦੰਦ ਡਿੱਗਣ, ਅਨੀਮੀਆ ਆਦਿ ਦੀ ਤਕਲੀਫ ਹੋ ਜਾਂਦੀ ਹੈ ।

4. ਅਸਧਾਰਨ ਸਮੇਂ ਵਿਚ ਕੰਮ ਕਰਨ ਨਾਲ ਪੈਦਾ ਹੋਣ ਵਾਲੇ ਰੋਗ (Diseases due to unusual timings of the Workers) – ਅੱਜ ਦੇ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਵਿਚ ਸੰਸਾਰ ਵਿਚ ਤਕਨੀਕੀ ਵਿਕਾਸ ਹੋ ਰਿਹਾ ਹੈ । ਇਹ ਵੀ ਨੋਟਿਸ ਕੀਤਾ ਗਿਆ ਹੈ ਕਿ ਤਕਨੀਕੀ ਕੰਪਨੀਆਂ ਨੌਕਰੀ ਵੀ ਮੁਹੱਈਆ ਕਰਵਾ ਰਹੀਆਂ ਹਨ । ਇਹ ਕੰਪਨੀਆਂ ਭਾਰਤ ਵਿਚ ਵੀ ਨੌਕਰੀਆਂ ਮੁਹੱਈਆ ਕਰਵਾ ਰਹੀਆਂ ਹਨ, ਪਰ ਦਿਨ-ਰਾਤ ਦੇ ਅੰਤਰ ਵਜੋਂ ਕਰਮਚਾਰੀਆਂ ਨੂੰ ਰਾਤ ਨੂੰ ਜਾਂ ਫਿਰ ਸ਼ਾਮ ਦੀ ਸਿਫਟ ਵਿਚ ਕੰਮ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਉਹਨਾਂ ਨੂੰ ਜੀਵਨ-ਸ਼ੈਲੀ ਸੰਬੰਧਿਤ ਰੋਗਾਂ ਦਾ ਸ਼ਿਕਾਰ ਹੋਣਾ ਪੈ ਰਿਹਾ ਹੈ । ਇਹ ਰੋਗ ਜਿਵੇਂ ਕਿ ਡਾਇਬਟੀਜ਼, ਹਾਈ ਪ੍ਰੋਟੇਸ਼ਨ, ਇਨਸੋਮਨੀਆ ਨੀਂਦ ਨਾ ਆਉਣਾ ਆਦਿ . ਗਲਤ ਸਮੇਂ ਵਿਚ ਕੰਮ ਕਰਨ ਕਾਰਨ ਹੋ ਰਹੇ ਹਨ ।

PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes

August 9, 2024August 8, 2024 by Prasanna

Punjab State Board PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes Important Questions and Answers.

PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes

Very Short Answer Type Questions

Question 1.
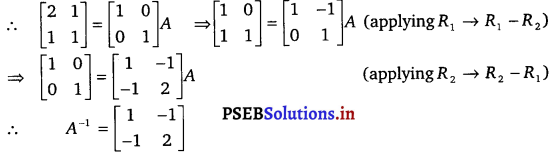
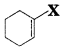Out of and PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 2 , which is an example of allylic halide?
X
Answer:
is an example of allylic halide.

Question 2.
Which of the following reactions is S_N1 type ?
PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 3
Answer:
Reaction (ii) is S_N1 reaction.

Question 3.
Which one of the following compounds is more easily hydrolysed by KOH and why?
CH₃CHClCH₂CH₃ or CH₃CH₂CH₂CH₂Cl
Answer:
Due to +1 effect of alkyl groups the 2° carbonium ion CH₃—CH—CH₂—CH₃ derived from sec-butyl chloride is more stable than the 1° carbonium ion \(\mathrm{CH}_{3}-\mathrm{CH}_{2}-\stackrel{+}{\mathrm{C}} \mathrm{H}_{2}\) derived from n-propyl chloride. Therefore sec-butyl chloride gets hydrolysed more easily than n-propyl chloride under S_N1 conditions.

Question 4.
What is known as a racemic mixture ? Give an example.
Answer:
equimolar mixture of a pair of enantiomers is called racemic mixture. A racemic mixture is optically inactive due to external compensation.

Question 5.
Consider the three types of replacement of group X by group Y as shown here.
PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 4
This can result in giving compound (A) or (B) or both. What is the process called if
(A) is the only compound obtained ?
(B) is the only compound obtained ?
(A) and (B) are formed in equal proportions ?
Answer:
(i) Retention
(ii) Inversion
(iii) Racemisation.

Question 6.
What is an asymmetric carbon?
Answer:
A carbon which is attached to four different atoms/groups is called asymmetric carbon. For example, the carbon atom in BrCHClI.

Question 7.
What is plane polarized light?
Answer:
A beam of light which has vibration in only one plane is called plane polarized light.

Question 8.
Why iodoform has appreciable antiseptic property ?
Answer:
Iodoform liberate I₂ when it comes in contact with skin. Antiseptic property of iodine is due to the liberation of I₂ not because of iodoform itself.
(responsible for antiseptic property)

Question 9.
How does the ordinary light differ from the plane polarized light?
Answer:
Ordinary light has oscillations in all the directions perpendicular to the path of propagation whereas plane polarised light has all oscillations in the same plane.

Question 10.
What do you .understand by the term optical activity of compounds?
Answer:
The property of certain compounds to rotate the plane of polarzed light in a characteristic way when it is passed through their solutions is called optical activity of compounds.

Short Answer Type Questions

Question 1.
Give reasons for the following:
(i) Ethyl iodide undergoes S_N2 reaction faster than ethyl bromide.
(ii) (±) 2-Butanol is optically inactive.
(iii) C—X bond length in halobenzene is smaller than C—X bond length in CH₃ —X.
Answer:
(i) Since I^– ion is a better leaving group than Br^– ion, hence, CH3I reacts faster than CH₃Br in SN₂ reaction with OH^– ion.

(ii) (±) 2-Butanol is a racemic mixture, i.e., there are two enantiomers in equal proportions. The rotation by one enantiomer will be cancelled by the rotation due to the other isomer, making the mixture optically inactive.

(iii) In CH₃—X the carbon atom is sp²-hybridised while in halobenzene the carbon atom is sp³-hybridised. The sp²-hybridised carbon is more electronegative due to greater s-character and holds the electron pair of C—X bond more tightly than sp³-hybridised carbon with less s-character. Thus, C—X bond length in CH₃—X is bigger than C—X in halobenzene.

Question 2.
Give reasons for the following:
(i) Haloalkanes easily dissolve in organic solvents.
(ii) Halogen compounds used in industry as solvents are alkyl chlorides rather than bromides and iodides.
Answer:
(i) Haloalkanes dissolve in organic solvents because the new intermolecular attractions between haloalkanes and organic solvent molecules have much the same strength as ones being broken in the separate haloalkanes and solvent molecules.
(ii) Because alkyl chlorides are more stable and more volatile than bromides and iodides.

Question 3.
Write the mechanism of the following reaction

Answer:
S_N2 mechanism
PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 7

Question 4.
Which would undergo S_N1 reaction faster in the following pairs and why ?
PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 8
Answer:
(i)
Tertiary halide reacts faster than primary halide because of greater stability of 3°-carbocation.

(ii) PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 10
Because the secondary carbocation formed in the slowest step is more stable than the primary carbocation.

Question 5.
Give reasons:
(i) n-Butyl bromide has higher boiling point than f-butyl bromide. Racemic mixture is optically inactive.
(ii) The presence of nitro group (—NO₂) at o/p positions increases the reactivity of haloarenes towards nucleophilic substitution reactions.
Answer:
(i) n-butyl bromide being a straight chain alkyl halide has larger surface area than tert butyl bromide. Larger the surface area, larger the magnitude of the van der Waal’s forces and hence higher is the boiling point.

(ii) A racemic mixture contains the two enantiomers d and l in equal •proportions. As the rotation due to one enantiomer is cancelled by equal and opposite rotation of another enantiomer, therefore, it is optically inactive.

(iii) The presence of NO₂ group at o/p position in haloarenes helps in the stabilisation of resulting carbanion by -R and -I effects and hence increases the reactivity of haloarenes towards nucleophilic substitution reactions.

Question 6.
(i) Why are alkyl halides insoluble in water ?
(ii) Why is butan-l-ol optically inactive but butan-2-ol is optically active ?
(iii) Although chlorine is an electron withdrawing group, yet it is ortho, para directing in electrophilic aromatic substitution reactions. Why ?
Answer:
(i) This is due to the inability of alkyl halide molecule to form intermolecular hydrogen bonds with water molecules.
(ii) PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 11
due to presence of a chiral carbon butan-2-ol is an optically active compound.

(iii) As the weaker resonance (+R) effect of Cl which stabilise the carbocation formed tends to oppose the stronger inductive (-I) effect of Cl which destabilise the carbocation at ortho and para positions and makes deactivation less for ortho and para position.

Question 7.
(i) Allyl chloride can be distinguished from vinyl chloride by NaOH and silver nitrate test. Comment.
(ii) Alkyl halide reacts with lithium aluminium hydride to give alkane. Name the attacking reagent which will bring out this change.
Answer:
(i) Vinyl chloride does not respond to NaOH and silver nitrate test because of partial double bond character due to resonance.
(ii) Hydride ion (H )

Question 8.
Give the ITJPAC name of the product formed when :
(i) 2-Methyl-l-bromopropane is treated with sodium in the presence of dry ether.
(ii) 1-Methyl cyclohexene is treated with HI.
(iii) Chloroethane is treated with silver nitrite.
Answer:
(i) 2, 5-dimethylhexane
(ii) 1 -Methyl-1 -iodocyclohexane
(iii) Nitroethane

Long Answer Type Questions

Question 1.
Some alkyl halides undergo substitution whereas some undergo elimination reaction on treatment with base. Discuss the structural features of alkyl halides with the help of examples which are responsible for this difference.
Answer:
Primary alkyl halides follow S_N2 mechanism in which a nucleophile attacks at 180° to the halogen atom. A transition state is formed in which carbon is bonded to two nucleophiles and finally halogen atom is pushed out. In S_N2 mechanism, substitution of nucleophile takes place as follows :
PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 12
Thus, in S_N2 mechanism, substitution takes place. Tertiary alkyl halides follow? S_N1 mechanism, In this case, tert-alkyl halides form 3° carbocation. Now, if the reagent used is a weak base then substitution occur while if it is a strong base then instead of substitution elimination occur.
PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 13
As alc. KOH is a strong base, so elimination competes over substitution and alkene is formed.

Question 2.
Why are aryl halides less reactive towards nucleophilic substitution reactions than alkyl halides ? How can we enhance the reactivity of aryl halides ?
Answer:
Aryl halides are less reactive towards nucleophilic substitution reaction due to the following reasons :
(i) In haloarenes, the lone pair of electron on halogen are in resonance with benzene ring. So, C—Cl bond acquires partial double bond character which strengthen C—Cl bond. Therefore, they are less reactive towards nucleophilic substitution reaction.
PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 14
(ii) In haloarenes, the carbon atom attached to halogen is sp²-hybridised. The sp²-hybridised carbon is more electronegative than sp³-hybridised carbon. This sp ²-hybridised carbon in haloarenes can hold the electron pair of C—X bond more tightly and make this C—Cl bond shorter than C—Cl bond haloalkanes.

(iii) Since, it is difficult to break a shorter bond than a longer bond therefore haloarenes are less reactive than haloarenes.
In haloarenes, the phenyl cation will not be stabilised by resonance therefore S_N1 mechanism ruled out.

(iv) Because of the repulsion between the nucleophile and electron rich arenes, aryl halides are less reactive than alkyl halides.

The reactivity of aryl halides can be increased by the presence of an electron withdrawing group (—NO₂) at ortho and para positions. However, no effect on reactivity of haloarenes is observed by the presence of electron withdrawing group at meta-position. Mechanism of the reaction is as depicted with OH^– ion.
PSEB 12th Class Chemistry Important Questions Chapter 10 Haloalkanes and Haloarenes 15

From the above resonance, it is very clear that electron density is rich at ortho and para positions. So, presence of EWG will facilitate nucleophilic at ortho and para positions not on meta position.

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.4

August 9, 2024August 8, 2024 by Bhagya

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.4

Dfrectlon (1 – 2): Write minors and cofactors of the elements of following determinants.

Question 1.
(i) \(\left|\begin{array}{cc}
2 & -4 \\
0 & 3
\end{array}\right|\)

(ii) \(\left|\begin{array}{ll}
\boldsymbol{a} & \boldsymbol{c} \\
\boldsymbol{b} & \boldsymbol{d}
\end{array}\right|\)
Solution.
(i) The given determinants is \(\left|\begin{array}{cc}
2 & -4 \\
0 & 3
\end{array}\right|\)
Minor of elements a_ij is M_ij.
∴ M₁₁ = Minor of element a₁₁ = 3
M₁₂ = Minor of element a₁₂= 0
M₂₁ = Minor of element a₂₁ = – 4
M₂₂ = Minor of element a₂₂ = 2

Cofactor of a_ij is = (- 1)^{i + j} M_ij.

∴ A₁₁ = (- 1)^{1 + 1} M₁₁ = (- 1)² (2) = 3
A₁₂ = (- 1)^{1 + 2} M₁₂ = (- 1)³ (0) = 0
A₂₁ = (- 1)^{2 + 1} M₂₁ = (- 1)³ (- 4) = 4
A₂₂ = (- 1)^{2 + 2} M₂₂ = (- 1)⁴ (2) = 2

(ii) The given determinant is \(\left|\begin{array}{ll}
a & c \\
b & d
\end{array}\right|\)
Minor of element a_ij is M_ij.
∴ M₁₁ = Minor of element a₁₁ = d
M₁₂ = Minor of element a₁₂= b
M₂₁ = Minor of element a₂₁ = c
M₂₂ = Minor of element a₂₂ = a

Cofactor of a_ij is = (- 1)^{i + j} M_ij.

∴ A₁₁ = (- 1)^{1 + 1} M₁₁ = (- 1)² (d) = d
A₁₂ = (- 1)^{1 + 2} M₁₂ = (- 1)³ (b) = – b
A₂₁ = (- 1)^{2 + 1} M₂₁ = (- 1)³ (c) = – c
A₂₂ = (- 1)^{2 + 2} M₂₂ = (- 1)⁴ (a) = a.

Question 2.
(i) \(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)

(ii) \(\left|\begin{array}{ccc}
1 & 0 & 4 \\
3 & 5 & -1 \\
0 & 1 & 2
\end{array}\right|\)
Solution.
100
The given determinant is \(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)
By the definition of minors and cofactors, we have

M₁₁ = Minor of A₁₁ = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1

M₁₂ = Minor of A₁₂ = \(\left|\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right|\) = 0.

M₁₃ = Minor of A₁₃ = \(\left|\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right|\) = 0

M₂₁ = Minor of A₂₁ = \(\left|\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right|\) = 0

M₂₂ = Minor of A₂₂ = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1

M₂₃ = Minor of A₂₃ = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right|\) = 0

M₃₁ = Minor of A₃₁ = \(\left|\begin{array}{ll}
0 & 0 \\
1 & 0
\end{array}\right|\) = 0

M₃₂ = Minor of A₃₂ = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right|\) = 0

M₃₃ = Minor of A₃₃ = \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1.

A₁₁ = Cofactor of a₁₁ = (- 1)^{1 + 1} M₁₁ = 1
A₁₂ = Cofactor of a₁₂ = (- 1)^{1 + 2} M₁₂ = 0
A₁₃ = Cofactor of a₁₃ = (-1)^{1 + 3} M₁₃ = 0
A₂₁ = Cofactor of a₂₁ = (- 1)^{2 + 1} M₂₁ = 0
A₂₂ = Cofactor of a₂₂ = (- 1)^{2 + 2} M₂₂ = 1
A₂₃ = Cofactor of a₂₃ = (- 1)^{2 + 3} M₂₃ = 0
A₃₁ = Cofactor of a₃₁ = (- 1)^{3 + 1} M₃₁ = 0
A₃₂ = Cofactor of a₃₂ = (-1)^{3 + 2} M₃₂ = 0
A₃₃ = Cofactor of a₃₃ = (-1)^{3 + 3} M₃₃ = 1

(ii) The given determinant is \(\left|\begin{array}{ccc}
1 & 0 & 4 \\
3 & 5 & -1 \\
0 & 1 & 2
\end{array}\right|\)
By definition of minors and cofactors, we have

M₁₁ = Minor of a₁₁
= \(\left|\begin{array}{cc}
5 & -1 \\
1 & 2
\end{array}\right|\) = 10 + 1 = 11

M₁₂ = Minor of a₁₂
= \(\left|\begin{array}{cc}
3 & -1 \\
0 & 2
\end{array}\right|\) = 6 – 0 = 6

M₁₃ = Minor of a₁₃
= \(\left|\begin{array}{ll}
3 & 5 \\
0 & 1
\end{array}\right|\) = 3 – 0 = 3

M₂₁ = Minor of a₂₁
= \(\left|\begin{array}{ll}
0 & 4 \\
1 & 2
\end{array}\right|\) = 0 – 4 = – 4

M₂₂ = Minor of a₂₂
= \(\left|\begin{array}{ll}
1 & 4 \\
0 & 2
\end{array}\right|\) = 2 – 0 = 2

M₂₃ = Minor of a₂₃
= \(\left|\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right|\) = 1 – 0 = 1

M₃₁ = Minor of a₃₁
= \(\left|\begin{array}{cc}
0 & 4 \\
5 & -1
\end{array}\right|\) = 0 – 20 = – 20

M₃₂ = Minor of a₃₂
= \(\left|\begin{array}{cc}
1 & 4 \\
3 & -1
\end{array}\right|\) = – 1 – 12 = – 13

M₃₃ = Minor of a₃₃
= \(\left|\begin{array}{ll}
1 & 0 \\
3 & 5
\end{array}\right|\) = 5 – 0 = 5.

Cofactor of a_ij = (- 1)^{i + j} M_ij

A₁₁ = Cofactor of a₁₁ = (- 1)^{1 + 1} M₁₁ = 11
A₁₂ = Cofactor of a₁₂ = (- 1)^{1 + 2} M₁₂ = – 6
A₁₃ = Cofactor of a₁₃ = (- 1)^{1 + 3} M₁₃ = 3
A₂₁ = Cofactor of a₂₁ = (- 1)^{2 + 1} M₂₁ = 4
A₂₂ = Cofactor of a₂₂ = (- 1)^{2 + 2} M₂₂ = 2
A₂₃ = Cofactor of a₂₃ = (- 1)^{2 + 3} M₂₃ = – 1
A₃₁ = Cofactor of a₃₁ = (- 1)^{3 + 1} M₃₁ = – 20
A₃₂ = Cofactor of a₃₂ = (- 1)^{3 + 2} M₃₂ = 13
A₃₃ = Cofactor of a₃₃ = (- 1)^{3 + 3} M₃₃ = 5

Question 3.
Using cofactors of elements of second row, evaluate ∆ = \(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\).
Solution.
The given determinant is \(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\)
We have,
M₂₁ = \(\left|\begin{array}{ll}
3 & 8 \\
2 & 3
\end{array}\right|\) = 9 – 16 = – 7
∴ A₂₁ = Cofactor of a₂₁ = (- 1)^{2 + 1} = 7

M₂₂ = \(\left|\begin{array}{ll}
5 & 8 \\
1 & 3
\end{array}\right|\) = 15 – 8 = 7
∴ A₂₂ = Cofactor of a₂₂ = (- 1)^{2 + 1} = 7

M₂₃ = \(\left|\begin{array}{ll}
5 & 3 \\
1 & 2
\end{array}\right|\)
∴ A₂₃ = Cofactor of a₂₃ = (- 1)^{2 + 3} M₂₃ = – 7
We know that is equal to the sum of the product of the elements of the second row with their corresponding cofactors.
∴ ∆ = a₂₁A₂₁ + a₂₂A₂₂ + a₂₃A₂₃
= 2 (7) + 0 (7) + 1 (- 7) = 14 – 7 = 7.

Question 4.
Using cofactors of elements of third column, evaluate
∆ = \(\left|\begin{array}{lll}
1 & x & y z \\
1 & y & z x \\
1 & x & x y
\end{array}\right|\)
Solution.
The given determinant is \(\left|\begin{array}{lll}
1 & x & y z \\
1 & y & z x \\
1 & x & x y
\end{array}\right|\)
We have,
M₁₃ = \(\left|\begin{array}{ll}
1 & y \\
1 & z
\end{array}\right|\) = z – y

M₂₃ = \(\left|\begin{array}{ll}
1 & x \\
1 & z
\end{array}\right|\) = z – x

M₃₃ = \(\left|\begin{array}{ll}
1 & x \\
1 & y
\end{array}\right|\) = y – x

∴ A₁₃ = Cofactor of a₁₃ = (- 1)^{1 + 3} M₁₃ = (z – y)
A₂₃ = Cofactor of a₂₃ = (- 1)^{2 + 3} M₂₃ = – (z – x) = (x – z)
A₃₃ = Cofactor of a₃₃ = (- 1 )^{3 + 3} M₃₃ = (y – x)
We know that ∆ is equal to the sum of the product of the elements of the second row with their corresponding cofactors.

∴ ∆ = a₁₃A₁₃ + a₂₃A₂₃ + a₃₃A₃₃
= yz (z – y) + zx (x – z) + xy (y – x)
= yz² – y²z + x²z – xz² + xy² – x²y
= (x²z – y²z) + (yz² – xz²) + (xy² – x²y)
= z(x² – y²) + z² (y – x) + xy (y – x)
= z(x – y)(x + y) + z² (y – x) + xy (y – x)
= (x – y)[zx + zy – z² – xy]
= (x – y) [z(x – z) + y(z – x)]
= (x – y) (z – x)[- z + y]
= (x – y) (y – z) (z – x)
Hence, A = (x – y)(y – z)(z – x)

Question 5.
If ∆ = \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\) and A_ij is cofactor of a_ij, then value of ∆ is given by
(A) a₁₁A₃₁ + a₁₂A₃₂ + a₁₃A₃₃
(B) a₁₁A₁₁ + a₁₂A₂₁ + a₁₃A₃₁
(C) a₂₁A₁₁ + a₂₂A₁₂ + a₂₃A₁₃
(D) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁
Solution.
∆ is equal to the sum of the products of the elements of a row (or a column) with their corresponding cofactors.
∆ = a₁₁A₁₁ + a₁₂A₁₂ + a₁₃A₁₃ or
a₂₁A₂₁ + a₂₂A₂₂ + a₂₃A₂₃ or
a₃₁A₃₁ + a₃₂A₃₂ + a₃₃A₃₃ or

a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁ or
a₁₂A₁₂ + a₂₂A₂₂ + a₃₂A₃₂ or
a₁₃A₁₃ + a₂₃A₂₃ + a₃₃A₃₃

Sum of the products of the elements of first column with their corresponding cofactors is ∆ = a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁
Hence, the correct answer is (D).

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.1

August 9, 2024August 8, 2024 by Bhagya

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.1

Direction (1 – 2): Evaluate the determinants.

Question 1.
\(\left|\begin{array}{cc}
2 & 4 \\
-5 & -1
\end{array}\right|\)
Solution.
Let A = \(\left|\begin{array}{cc}
2 & 4 \\
-5 & -1
\end{array}\right|\)
∴ |A| = 2(- 1) – 4(- 5) = – 2 + 20 = 18.

Question 2.
(i) \(\left|\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right|\)

(ii) \(\left|\begin{array}{cc}
x^{2}-x+1 & x-1 \\
x+1 & x+1
\end{array}\right|\)
solution.
(i) \(\left|\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right|\) = (cos θ) (cos θ) – (- sin θ)(sin θ)
= cos² θ + sin² θ = 1

(ii) \(\left|\begin{array}{cc}
x^{2}-x+1 & x-1 \\
x+1 & x+1
\end{array}\right|\) = (x² – x + 1) (x + 1) – (x – 1) (x + 1)
= x³ – x² + x + x² – x + 1 – (x² – 1)
= x³ + 1 – x² + 1
= x³ – x² + 2.

Question 3.
If A = \(\left[\begin{array}{ll}
1 & 2 \\
4 & 2
\end{array}\right]\) then show that [2A] = 4|A|
Solution.
The given matrix is A = \(\left[\begin{array}{ll}
1 & 2 \\
4 & 2
\end{array}\right]\)
2A = \(2\left[\begin{array}{ll}
1 & 2 \\
4 & 2
\end{array}\right]=\left[\begin{array}{ll}
2 & 4 \\
8 & 4
\end{array}\right]\)
L.H.S.= |2A|
= \(\left|\begin{array}{ll}
2 & 4 \\
8 & 4
\end{array}\right|\)
= 2 × 4 – 4 × 8
= 8 – 32 = – 24

Now, |A| = \(\left|\begin{array}{ll}
1 & 2 \\
4 & 2
\end{array}\right|\)
= 1 × 2 – 2 × 4 = 2 – 8 = – 6
∴ R.H.S.= 4|A| = 4 × (- 6) = – 24
∴ L.H.S. = R.H.S.

Question 4.
If A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 1 & 2 \\
0 & 0 & 4
\end{array}\right]\),then show that |3A| = 27|A|.
Solution.
The given matrix is A = \(\left[\begin{array}{lll}
1 & 0 & 1 \\
0 & 1 & 2 \\
0 & 0 & 4
\end{array}\right]\)

It can be observed that in the first column, two entries are zero. Thus, we expand the matrix A along the first column (C₁) for finding |A|.

PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.1 1

From Eqs. (j) and (ii), we have,
|3A| = 27 |A|
Hence, the given result is proved.

Question 5.
Evaluate the following determinants:
(i) \(\left|\begin{array}{ccc}
3 & -1 & -2 \\
0 & 0 & -1 \\
3 & -5 & 0
\end{array}\right|\)

(ii) \(\left|\begin{array}{ccc}
3 & -4 & 5 \\
1 & 1 & -2 \\
2 & 3 & 1
\end{array}\right|\)

(iii) \(\left|\begin{array}{ccc}
0 & 1 & 2 \\
-1 & 0 & -3 \\
-2 & 3 & 0
\end{array}\right|\)

(iv) \(\left[\begin{array}{ccc}
2 & -1 & -2 \\
0 & 2 & -1 \\
3 & -5 & 0
\end{array}\right]\)

Solution.
(i) Let A = \(\left|\begin{array}{ccc}
3 & -1 & -2 \\
0 & 0 & -1 \\
3 & -5 & 0
\end{array}\right|\)

It can be observed that in the second row, two entries are zero. Thus, we expand along the second row for easier calculation.

|A| = \(0\left|\begin{array}{cc}
-1 & -2 \\
-5 & 0
\end{array}\right|+0\left|\begin{array}{cc}
3 & -2 \\
3 & 0
\end{array}\right|-(-1)\left|\begin{array}{cc}
3 & -1 \\
3 & -5
\end{array}\right|\)
= – 15 + 3 = – 12

(ii) Let A = \(\left|\begin{array}{ccc}
3 & -4 & 5 \\
1 & 1 & -2 \\
2 & 3 & 1
\end{array}\right|\)
By expanding along the first row, we have
|A| = \(3\left|\begin{array}{cc}
1 & -2 \\
3 & 1
\end{array}\right|+4\left|\begin{array}{cc}
1 & -2 \\
2 & 1
\end{array}\right|+5\left|\begin{array}{ll}
1 & 1 \\
2 & 3
\end{array}\right|\)

= 3 (1 + 6) + 4 (1 + 4) + 5 (3 – 2)
= 3(7) + 4(5) + 5(1)
= 21 + 20 + 5 = 46.

(iii) \(\left|\begin{array}{ccc}
0 & 1 & 2 \\
-1 & 0 & -3 \\
-2 & 3 & 0
\end{array}\right|\)
By expanding along the first row, we have
|A| = \(0\left|\begin{array}{cc}
0 & -3 \\
3 & 0
\end{array}\right|-1\left|\begin{array}{cc}
-1 & -3 \\
-2 & 0
\end{array}\right|+2\left|\begin{array}{cc}
-1 & 0 \\
-2 & 3
\end{array}\right|\)
= 0 – 1(0 – 6) + 2(- 3 – 0)
= – 1(- 6) + 2 (- 3) = 6 – 6 = 0

(iv) \(\left[\begin{array}{ccc}
2 & -1 & -2 \\
0 & 2 & -1 \\
3 & -5 & 0
\end{array}\right]\)
By expanding along the first row, we have
|A| = \(2\left|\begin{array}{cc}
2 & -1 \\
-5 & 0
\end{array}\right|-0\left|\begin{array}{cc}
-1 & -2 \\
-5 & 0
\end{array}\right|+3\left|\begin{array}{cc}
-1 & -2 \\
2 & -1
\end{array}\right|\)
= 2(0 – 5) – 0 + 3 (1 + 4)
= – 10 + 15 = 5.

Question 6.
If A = \(\left[\begin{array}{ccc}
1 & 1 & -2 \\
2 & 1 & -3 \\
5 & 4 & -9
\end{array}\right]\), find |A|.
Solution.
Let A = \(\left[\begin{array}{ccc}
1 & 1 & -2 \\
2 & 1 & -3 \\
5 & 4 & -9
\end{array}\right]\)

By expanding along the first row, we have

|A| = \(1\left|\begin{array}{cc}
1 & -3 \\
4 & -9
\end{array}\right|-1\left|\begin{array}{cc}
2 & -3 \\
5 & -9
\end{array}\right|-2\left|\begin{array}{ll}
2 & 1 \\
5 & 4
\end{array}\right|\)
= 1 (- 9 + 12) – 1 (- 18 + 15) – 2 (8 – 5)
= 1 (3) – 1 (- 3) – 2 (3)
= 3 + 3 – 6
= 6 – 6 = 0.

Question 7.
Find values of x, if
(i) \(\left|\begin{array}{ll}
2 & 4 \\
5 & 1
\end{array}\right|=\left|\begin{array}{cc}
2 x & 4 \\
6 & x
\end{array}\right|\)

(ii) \(\left|\begin{array}{ll}
2 & 3 \\
4 & 5
\end{array}\right|=\left|\begin{array}{cc}
x & 3 \\
2 x & 5
\end{array}\right|\)
Solution.
(i) Given, \(\left|\begin{array}{ll}
2 & 4 \\
5 & 1
\end{array}\right|=\left|\begin{array}{cc}
2 x & 4 \\
6 & x
\end{array}\right|\)

On expending both determinants, we get
⇒ 2 × 1 – 5 × 4 = 2 × x – 6 × 4
⇒ 2 – 20 = 2x² – 24
⇒ 2x² = 6
⇒ x² = 3
⇒ x = ±√3.

(ii) \(\left|\begin{array}{ll}
2 & 3 \\
4 & 5
\end{array}\right|=\left|\begin{array}{cc}
x & 3 \\
2 x & 5
\end{array}\right|\)

On expending both determinants, we get
⇒ 2 × 5 – 3 × 4 = x × 5 – 3 × 2x
⇒ 10 – 12 = 5x – 6x
⇒ – 2 = – x
⇒ x = 2.

Question 8.
If \(\left|\begin{array}{cc}
x & 2 \\
18 & x
\end{array}\right|=\left|\begin{array}{cc}
6 & 2 \\
18 & 6
\end{array}\right|\), then x is equal to
(A) 6
(B) ± 6
(C) – 6
(D) 0
Solution.
Given, \(\left|\begin{array}{cc}
x & 2 \\
18 & x
\end{array}\right|=\left|\begin{array}{cc}
6 & 2 \\
18 & 6
\end{array}\right|\)

On expending both determinants, we get
⇒ x² – 36 = 36 – 36
⇒ x² – 36 = 0
⇒ x² – 36 = 0
⇒ x = ± 6.
Hence, the correct answer is (B).

PSEB 12th Class Maths Solutions Chapter 3 Matrices Miscellaneous Exercise

August 9, 2024August 8, 2024 by Bhagya

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3 Matrices Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Miscellaneous Exercise

Question 1.
Let A = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\), show that (aI + bA)ⁿ = aⁿI + na^{n – 1}bA, where I is the identity matrix of order 2 and n ∈ N.
Solution.
It is given that A = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\)
To show:
P(n): {aI + bA)ⁿ =(aI + bA)ⁿ = aⁿI + na^{n – 1}bA, n ∈ N.
We shall prove that the result by using the principle of mathematical induction.
For n = 1, we have
P(1): (aI + bA) = aI + ba°A = aI + bA
Therefore, the result is true for n = 1.
Let the result be true for n = k.
That is, P(k): (aI + bA)^k = a^kI = ka^{k – 1} bA
Now, we prove that the result is true for n = k +1.
Consider
(aI + bA)^{k + 1} = (aI + bA)^k (aI + bA)
(∵ a^{x + y} = a^x x a^y)
= (a^kI + ka^{k – 1}bA) (aI + bA)
= a^{k + 1} I + ka^kbAI + a^kbIA + ka^{k – 1} b²A²
= a^{k + 1}I + (k + 1)a^kbA + ka^{k – 1}b²A²

Now, A² = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\) = 0

From Eq. (i) we have,
(aI + bA)^{k + 1} = a^{k + 1}I + (k + 1)a^kbA + 0
= a^{k + 1}I + (k + 1)a^kbA

Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have
(aI + bA)ⁿ = aⁿI + na^{n – 1}bA, where A = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\) n ∈ N.

Question 2.
If A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\), prove that Aⁿ = \(\left[\begin{array}{lll}
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1}
\end{array}\right]\), n ∈ N.
Solution.
It is given that A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\)
To show:
P(n) = Aⁿ = \(\left[\begin{array}{lll}
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1}
\end{array}\right]\), n ∈ N

We shall prove the result by using the principle of mathematical induction.
For n= 1, we have
P(1) = \(\left[\begin{array}{lll}
3^{1-1} & 3^{1-1} & 3^{1-1} \\
3^{1-1} & 3^{1-1} & 3^{1-1} \\
3^{1-1} & 3^{1-1} & 3^{1-1}
\end{array}\right]=\left[\begin{array}{lll}
3^{0} & 3^{0} & 3^{0} \\
3^{0} & 3^{0} & 3^{0} \\
3^{0} & 3^{0} & 3^{0}
\end{array}\right]=\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\) = A
Therefore, the result is true for n = 1.
Let the result be true for n = k.
i.e., P(k) = A^k = \(\left[\begin{array}{lll}
3^{k-1} & 3^{k-1} & 3^{k-1} \\
3^{k-1} & 3^{k-1} & 3^{k-1} \\
3^{k-1} & 3^{k-1} & 3^{k-1}
\end{array}\right]\)
Now, we prove that the result is true for n = k + 1.
Now, A^{k + 1} = A . A^k
= \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\left[\begin{array}{lll}
3^{k-1} & 3^{k-1} & 3^{k-1} \\
3^{k-1} & 3^{k-1} & 3^{k-1} \\
3^{k-1} & 3^{k-1} & 3^{k-1}
\end{array}\right]\)

= \(\left[\begin{array}{lll}
3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} \\
3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} \\
3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} & 3 \cdot 3^{k-1}
\end{array}\right]=\left[\begin{array}{lll}
3^{(k+1)-1} & 3^{(k+1)-1} & 3^{(k+1)-1} \\
3^{(k+1)-1} & 3^{(k+1)-1} & 3^{(k+1)-1} \\
3^{(k+1)-1} & 3^{(k+1)-1} & 3^{(k+1)-1}
\end{array}\right]\)

Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have
Aⁿ = \(\left[\begin{array}{lll}
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1}
\end{array}\right]\), n ∈ N.

Question 3.
If A = \(\left[\begin{array}{rr}
3 & -4 \\
1 & -1
\end{array}\right]\), then prove Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), where n is any positive integer.
Solution.
It is given that A = \(\left[\begin{array}{rr}
3 & -4 \\
1 & -1
\end{array}\right]\)

To prove:
P(n) : Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), n ∈ N
We shall prove that result by using the principle of mathematical induction.
For n = 1, we have
P(1) : A¹ = \(\left[\begin{array}{cc}
1+2 & -4 \\
1 & 1-2
\end{array}\right]=\left[\begin{array}{cc}
3 & -4 \\
1 & -1
\end{array}\right]\) = A

Therefore, the result is true for n = 1.
Let the result be true for n = k.

i.e., p(k) = A^k = \(\left[\begin{array}{cc}
1+2 k & -4 k \\
k & 1-2 k
\end{array}\right]\), n ∈ N

Now, we prove that the result is true for n = k +1.
Consider A^k+1 = A^k . A

PSEB 12th Class Maths Solutions Chapter 3 Matrices Miscellaneous Exercise 1

Therefore, the result is true for n = k +1.
Thus, by the principle of mathematical induction, we have

Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), n ∈ N.

Question 4.
If A and B are symmetric matrices, prove that AB – BA is a skew symmetric matrix.
Solution.
It is given that A and B are symmetric matrices. Therefore, we have
A’ = A and B’ = B …………..(i)
Now, (AB – BA)’ = (AB)’ – (BA)’ [(A -B)’ = A’ – B’]
= B’A’ – A’B’ [(AB)’ = B’A’]
= BA – AB [UsingEq. (i)]
= – (AB – BA)
∴ (AB – BA)’ = – (AB – BA)
Thus, (AB – BA) is a skew symmetric matrix.

Question 5.
Show that the matrix B’ AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.
Solution.
We suppose that A is a symmetric matrix, then A’ = A ………… (i)
Consider
(B’ABX = {B’ (AB)}’
= (AB)’ (B’)’ [(AB)’ = B’A’]
= B’A'(B) [∵ (B’)’ = B]
= B'(A’B)
= B'(AB) [Using Eq. (i)]
∴ (B’AB)’ = B’ AB
Thus, if A is a symmetric matrix, then B’AB is a symmetric matrix.
Now, we suppose that A is a skew symmetric matrix.
Then, A’ = – A
Consider
(B’AB)’ = [B’ (AB)]’ = (AB)’ (B’ )’ [∵ (AB)’ = B’A’ and (A’)’ = A]
= (B’A’)B = B’ (-A)B
= – B’AB
∴ (B’ AB)’ = – B’ AB
Thus, if A is a skew-symmetric matrix, then B’ AB is a skew symmetric matrix.
Hence, if A is a symmetric or skew symmetric matrix, then B’AB is a symmetric or skew symmetric matrix accordingly.

Question 6.
Find the values of x, y and z if the matrix A = \(\left[\begin{array}{ccc}
0 & 2 y & z \\
x & y & -z \\
x & -y & z
\end{array}\right]\) satisfy the equation A’ A = I.
Solution.
Given, A’A = I

PSEB 12th Class Maths Solutions Chapter 3 Matrices Miscellaneous Exercise 2

On comparing the corresponding elements, we have
2x² = 1,
⇒ x² = \(\frac{1}{2}\),
⇒ x = ± \(\frac{1}{\sqrt{2}}\)

6y² = 1,
⇒ y² = \(\frac{1}{6}\),
⇒ y = ± \(\frac{1}{\sqrt{6}}\)

3z² = 1
⇒ z² = \(\frac{1}{3}\)
⇒ z = ± \frac{1}{\sqrt{3}}\(\).

Question 7.
For what values of x:[1 2 1] \(\left[\begin{array}{lll}
1 & 2 & 0 \\
2 & 0 & 1 \\
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0?
Solution.
We have [1 2 1] \(\left[\begin{array}{lll}
1 & 2 & 0 \\
2 & 0 & 1 \\
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0
⇒ [1 + 4 + 1 2 + 0 + 0 0 + 2 + 2] \(\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0

⇒ [6 2 4] \(\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0
⇒ [6(0) + 2(2) + 4(x)]= 0
[4 + 4x] = [0]
∴ 4 + 4x = 0
⇒ x = – 1
Thus, the required value of x is – 1.

Question 8.
If A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\) show that A² – 5A + 7I = 0.
Solution.
k is given that A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\)

PSEB 12th Class Maths Solutions Chapter 3 Matrices Miscellaneous Exercise 3

Question 9.
Find x, if [x – 5 – 1] \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\left[\begin{array}{c}
x \\
4 \\
1
\end{array}\right]\) = 0.
Solution.
[x – 5 – 1] \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\left[\begin{array}{c}
x \\
4 \\
1
\end{array}\right]\)

⇒ [x + 0 – 2 0 – 10 + 0 2x – 5 – 3] \(\left[\begin{array}{l}
x \\
4 \\
1
\end{array}\right]\) = 0
⇒ [x – 2 -10 2x – 8] \(\left[\begin{array}{l}
x \\
4 \\
1
\end{array}\right]\) = 0

⇒ [x(x – 2) – 40 + 2x – 8] = 0
⇒ [x² – 2x – 40 + 2x – 8] = 0
⇒ [x² – 48] = [0]
⇒ x² – 48 = 0
⇒ x² = 48
⇒ x = ± 4√3.

Question 10.
A manufacturer produces three products x, y, z which he sells in two markets.
Annual sales are indicated below

PSEB 12th Class Maths Solutions Chapter 3 Matrices Miscellaneous Exercise 4

(a) If unit sale prices of x, y and z are ₹ 2.50, ₹ 1.50 and ₹ 1.00, respectively, then find the total revenue In each market with the help of matrix algebra.
(b) If the unit costs of the above three commodities are ₹ 2.00, ₹ 1.00 and 50 paise respectively. Find the gross profit.
Solution.
(a) The unit sale prices of x, y and z are respectively given as ₹ 2.50, ₹ 1.50, and ₹ 1.00.
Consequently, the total revenue in market I can be represented in the form of a matrix as
[10000 2000 18000] \(\left[\begin{array}{l}
2.50 \\
1.50 \\
1.00
\end{array}\right]\)
= 10000 × 2.50 + 2000 × 1.50 + 18000 × 1.00
= 25000 +3000 + 18000 = 46000
The total revenue in market II can be represented in the form of a matrix as
[6000 2000 8000] \(\left[\begin{array}{l}
2.50 \\
1.50 \\
1.00
\end{array}\right]\)
= 6000 × 2.50 + 20000 × 1.50 + 8000 × 1.00
= 15000 + 30000 + 8000 = 53000
Therefore, the total revenue in market I is ₹ 46000 and the same in market II is ₹ 53000.

(b) The unit cost prices of x, y, and z are respectively given as 2.00, U.00, and 50 paise.
Consequently, the total cost prices of all the products in market I can be represented in the form of a matrix as
[10000 2000 18000] \(\left[\begin{array}{l}
2.00 \\
1.00 \\
0.50
\end{array}\right]\)
= 10000 × 2.00 + 2000 × 1.00 + 18000 × 0.50
= 20000 + 2000 + 9000 = 31000
Since the total revenue in market I is ₹ 46000, the gross profit in this market is (₹ 46000 – ₹ 31000) = ₹ 15000.
The total cost prices of all the products in market Il can be represented in the form of a matrix as
[6000 20000 8000] \(\left[\begin{array}{l}
2.00 \\
1.00 \\
0.50
\end{array}\right]\)
= 6000 × 2.00 + 20000 × 1.00 + 8000 × 0.50
= 12000 + 20000 + 4000 = 36000
Since the total revenue in market is ₹ 53000, the gross profit in this market is ( 53000 – 36000) = 17000.
Total gross profit = ₹ (15000 + 17000) = ₹ 32000.

Question 11.
Find the matrix X so that X \(\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right]\) = \(\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)
Solution.
It is given that

\(\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right]\) = \(\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)

The matrix given on the R.H.S. of the equation is a 2 × 3 matrix and the one given on the L.H.S. of the equation is a 2 × 3 matrix. Therefore, X has to be a 2 × 2 matrix.
Now, let x = \(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\)
Therefore, we have

\(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right]=\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)

⇒ \(\left[\begin{array}{ccc}
a+4 c & 2 a+5 c & 3 a+6 c \\
b+4 d & 2 b+5 d & 3 b+6 d
\end{array}\right]=\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)

On equating the corresponding elements of the two matrices, we have
a + 4c = – 7,
b + 4d = 2,

2a + 5c = – 8,
2b + 5d = 4,

3a + 6c = – 9,
3b + 6d = 6

Now, a + 4c = – 7
⇒ a = – 7 – 4c

∴ 2a + 5c = – 8
⇒ – 14 – 8c + 5c = – 8
⇒ – 3c = 6
⇒ c = – 2
∴ a = – 7 – 4(- 2)
= – 7 + 8 = 1

Now, b + 4d = 2
⇒ b = 2 – 4d
∴ 2b + 5d = 4
⇒ 4 – 8d + 5d = 4
⇒ – 3d = 0
⇒ d = 0.
Thus, a = 1, b = 2, c = – 2, d = 0
Hence, the required matrix X is \(\left[\begin{array}{cc}
1 & -2 \\
2 & 0
\end{array}\right]\).

Question 12.
If A and B are square matrices of the same order such that AB = BA, then prove by induction that AB” = B” A. Further, provethat(AB)” =A”B” for all n ∈ N.
Solution.
A and B are square matrices of the same order such that AB = BA.
To prove:
P(n): ABⁿ = BⁿA, n e N
For n = 1,we have P(1): AB = BA (Given)
AB¹ = B¹A
Therefore, the result is true for n = 1.
Let the result be true for n = k.
P(k): AB^k = B^kA ………….(i)
Now, we prove that the result is true for n = k + 1.
AB^{k + 1} = AB^k . B = (B^kA)B [From Eq. (j)]
= B^k (AB) [By associative law]
= B^k (BA) [: AB = BA (Given)]
= (B^kB)A [By associative law]
= B^{k + 1} A
Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have
ABⁿ = BⁿA, n e N.
Now, we prove that (AB)ⁿ = AⁿBⁿ for all n ∈ N
For n = 1, we have
(AB)¹ = A¹B¹ = AB
Therefore, the result is true for n = 1.
Let the result be true for n = k.
(AB)^k = A^kB^k …………….(ii)
Now, we prove that the result is true for n = k + 1.
(AB)^{k + 1} = (AB)^k . (AB)
= (A^kB^k).(AB)
= A^k(B^kA)B
= A^k(AB^k)B
= (A^kA).(B^kB)
= A^{k + 1}B^{k + 1}
Therefore, the result is true for n = k +1.
Thus, by the principle of mathematical induction, we have (AB)ⁿ = AⁿBⁿ, for all natural numbers.

Direction (13 – 15) Choose the correct answer in the following questions.

Question 13.
If A = \(\left[\begin{array}{cc}
\alpha & \beta \\
\gamma & -\alpha
\end{array}\right]\) is such that A² = I, then
(A) 1 + α² + βγ = 0
(C) 1 – α² – βγ = 0
(B) 1 – α² + βγ = 0
(D) 1 + α² – βγ = 0
Solution.
We have, A = \(\left[\begin{array}{cc}
\alpha & \beta \\
\gamma & -\alpha
\end{array}\right]\)

PSEB 12th Class Maths Solutions Chapter 3 Matrices Miscellaneous Exercise 5

On comparing the corresponding elements, we have
α² + βγ = 1
α² + βγ – 1 = 0
1 – α² – βγ = 0
Hence, the correct answer is (C).

Question 14.
If the matrix A is both symmetric and skew symmetric, then
(A) A is a diagonal matrix
(B) A is a zero matrix
(C) A is a square matrix
(D) None of these
Solution.
If A is both symmetric and skew symmetric matrix, then we should have
A’ = A and A’ = – A
⇒ A = – A
⇒ A + A = 0
⇒ 2A = 0 A = 0
Therefore, A is a zero matrix.
Hence, the correct answer is (B).

Question 15.
If A is square matrix such that A² = A, then (I + A)³ – 7A is equal to
(A) A
(B) I – A
(C) I
(D)3A
Solution.
(I + A)³ – 7A = I³ + A³ + 3I²A + 3A²I – 7A
= I + A³ + 3A + 3A² – 7A
= I + A² . A + 3A + 3A – 7A [∵ A² = A (given)]
= I + A.A – A
= I + A² – A
I + A – A = 1
∴ (I + A)³ – 7A = 1
Hence, the correct answer is (C).

PSEB 12th Class Geography Book Solutions Guide in Punjabi English Medium

August 9, 2024August 8, 2024 by Veer

Punjab State Board Syllabus PSEB 12th Class Geography Book Solutions Guide Pdf in English Medium and Punjabi Medium are part of PSEB Solutions for Class 12.

PSEB 12th Class Geography Guide | Geography Guide for Class 12 PSEB

Geography Guide for Class 12 PSEB | PSEB 12th Class Geography Book Solutions

PSEB 12th Class Geography Book Solutions in Hindi Medium

PSEB 12th Class Geography Book Solutions in English Medium

Chapter 1 Human Geography and its Branches
Chapter 2 Human Resources – Population and its Change
Chapter 3 Human Resources – Human Development and Settlements
Chapter 4 Economic Geography – Agriculture and Overview (Activities of Primary Sector)
Chapter 5 Economic Geography – Minerals and Energy Resources
Chapter 6 Economic Geography Manufacturing (Secondary Care and Knowledge/Activities of Specialised Areas
Chapter 7 Transport, Communication and Trade
Chapter 8 Geographical Perspective on selected Issues
Chapter 9 Practical Geography

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2

August 9, 2024August 8, 2024 by Bhagya

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3 Matrices Ex 3.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.2

Question 1.
Let A = \(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\), C = \(\left[\begin{array}{cc}
-2 & 5 \\
3 & 4
\end{array}\right]\)
Find each of the following:
(i) A + B
(ii) A – B
(iii) 3A – C
(iv) AB
(v) BA
Solutions.
(i) A + B = \(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]+\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\)

= \(\left[\begin{array}{cc}
2+1 & 4+3 \\
3-2 & 2+5
\end{array}\right]=\left[\begin{array}{ll}
3 & 7 \\
1 & 7
\end{array}\right]\)

(ii) A – B = \(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]-\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\)

= \(\left[\begin{array}{cc}
2-1 & 4-3 \\
3-(-2) & 2-5
\end{array}\right]=\left[\begin{array}{cc}
1 & 1 \\
5 & -3
\end{array}\right]\)

(iii) 3A – C = 3\(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]-\left[\begin{array}{cc}
-2 & 5 \\
3 & 4
\end{array}\right]\)

= \(\left[\begin{array}{ll}
3 \times 2 & 3 \times 4 \\
3 \times 3 & 3 \times 2
\end{array}\right]-\left[\begin{array}{cc}
-2 & 5 \\
3 & 4
\end{array}\right]\)

= \(\left[\begin{array}{cc}
6 & 12 \\
9 & 6
\end{array}\right]-\left[\begin{array}{cc}
-2 & 5 \\
3 & 4
\end{array}\right]\)

= \(\left[\begin{array}{cc}
6+2 & 12-5 \\
9-3 & 6-4
\end{array}\right]\)

= \(\left[\begin{array}{ll}
8 & 7 \\
6 & 2
\end{array}\right]\)

(iv) Matrix A has 2 columns. This number is equal to the number of rows in matrix B. Therefore, AB is defined as
AB = \(\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\)

= \(\left[\begin{array}{ll}
2(1)+4(-2) & 2(3)+4(5) \\
3(1)+2(-2) & 3(3)+2(5)
\end{array}\right]\)

= \(\left[\begin{array}{ll}
2-8 & 6+20 \\
3-4 & 9+10
\end{array}\right]=\left[\begin{array}{ll}
-6 & 26 \\
-1 & 19
\end{array}\right]\)

(v) Matrix B has 2 columns. This number is equal to the number of rows in matrix A.
Therefore, BA is defined as
BA = \(\left[\begin{array}{cc}
1 & 3 \\
-2 & 5
\end{array}\right]\left[\begin{array}{ll}
2 & 4 \\
3 & 2
\end{array}\right]\)

= \(\left[\begin{array}{cc}
1(2)+3(3) & 1(4)+3(2) \\
-2(2)+5(3) & -2(4)+5(2)
\end{array}\right]\)

= \(\left[\begin{array}{cc}
2+9 & 4+6 \\
-4+15 & -8+10
\end{array}\right]=\left[\begin{array}{cc}
11 & 10 \\
11 & 2
\end{array}\right]\)

Question 2.
Compute the following:
(i) \(\left[\begin{array}{cc}
\boldsymbol{a} & \boldsymbol{b} \\
-\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]+\left[\begin{array}{cc}
\boldsymbol{a} & \boldsymbol{b} \\
\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
a^{2}+b^{2} & b^{2}+c^{2} \\
a^{2}+c^{2} & a^{2}+b^{2}
\end{array}\right]+\left[\begin{array}{cc}
2 a b & 2 b c \\
-2 a c & -2 a b
\end{array}\right]\)

(iii) \(\left[\begin{array}{ccc}
-1 & 4 & -6 \\
8 & 5 & 16 \\
2 & 8 & 5
\end{array}\right]+\left[\begin{array}{ccc}
12 & 7 & 6 \\
8 & 0 & 5 \\
3 & 2 & 4
\end{array}\right]\)

Solution.
(i) \(\left[\begin{array}{cc}
\boldsymbol{a} & \boldsymbol{b} \\
-\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]+\left[\begin{array}{cc}
\boldsymbol{a} & \boldsymbol{b} \\
\boldsymbol{b} & \boldsymbol{a}
\end{array}\right]\) = \(\left[\begin{array}{cc}
a+a & b+b \\
-b+b & a+a
\end{array}\right]=\left[\begin{array}{cc}
2 a & 2 b \\
0 & 2 a
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
a^{2}+b^{2} & b^{2}+c^{2} \\
a^{2}+c^{2} & a^{2}+b^{2}
\end{array}\right]+\left[\begin{array}{cc}
2 a b & 2 b c \\
-2 a c & -2 a b
\end{array}\right]\) = \(\left[\begin{array}{ll}
a^{2}+b^{2}+2 a b & b^{2}+c^{2}+2 b c \\
a^{2}+c^{2}-2 a c & a^{2}+b^{2}-2 a b
\end{array}\right]\)

= \(\left[\begin{array}{ll}
(a+b)^{2} & (b+c)^{2} \\
(a-c)^{2} & (a-b)^{2}
\end{array}\right]\).

(iii) \(\left[\begin{array}{ccc}
-1 & 4 & -6 \\
8 & 5 & 16 \\
2 & 8 & 5
\end{array}\right]+\left[\begin{array}{ccc}
12 & 7 & 6 \\
8 & 0 & 5 \\
3 & 2 & 4
\end{array}\right]\) = \(\left[\begin{array}{ccc}
-1+12 & 4+7 & -6+6 \\
8+8 & 5+0 & 16+5 \\
2+3 & 8+2 & 5+4
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
11 & 11 & 0 \\
16 & 5 & 21 \\
5 & 10 & 9
\end{array}\right]\)

(iv) \(\left[\begin{array}{cc}
\cos ^{2} x & \sin ^{2} x \\
\sin ^{2} x & \cos ^{2} x
\end{array}\right]+\left[\begin{array}{cc}
\sin ^{2} x & \cos ^{2} x \\
\cos ^{2} x & \sin ^{2} x
\end{array}\right]\) = \(\left[\begin{array}{ll}
\cos ^{2} x+\sin ^{2} x & \sin ^{2} x+\cos ^{2} x \\
\sin ^{2} x+\cos ^{2} x & \cos ^{2} x+\sin ^{2} x
\end{array}\right]\)

= \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\) [∵ sin² x + cos² x = 1].

Question 3.
Compute the indicated products:
(i) \(\left[\begin{array}{cc}
a & b \\
-b & a
\end{array}\right]\left[\begin{array}{cc}
a & -b \\
b & a
\end{array}\right]\)

(ii) \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\left[\begin{array}{lll}
2 & 3 & 4
\end{array}\right]\)

(iii) \(\left[\begin{array}{cc}
1 & -2 \\
2 & 3
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right]\)

(iv) \(\left[\begin{array}{lll}
2 & 3 & 4 \\
3 & 4 & 5 \\
4 & 5 & 6
\end{array}\right]\left[\begin{array}{ccc}
1 & -3 & 5 \\
0 & 2 & 4 \\
3 & 0 & 5
\end{array}\right]\)

(v) \(\left[\begin{array}{cc}
2 & 1 \\
3 & 2 \\
-1 & 1
\end{array}\right]\left[\begin{array}{ccc}
1 & 0 & 1 \\
-1 & 2 & 1
\end{array}\right]\)

(vi) \(\left[\begin{array}{ccc}
3 & -1 & 3 \\
-1 & 0 & 2
\end{array}\right]\left[\begin{array}{cc}
2 & -3 \\
1 & 0 \\
3 & 1
\end{array}\right]\)

Solution.
(i) \(\left[\begin{array}{cc}
a & b \\
-b & a
\end{array}\right]\left[\begin{array}{cc}
a & -b \\
b & a
\end{array}\right]\) = \(\left[\begin{array}{cc}
a(a)+b(b) & a(-b)+b(a) \\
-b(a)+a(b) & -b(-b)+a(a)
\end{array}\right]\)

=\(\left[\begin{array}{cc}
a^{2}+b^{2} & -a b+a b \\
-a b+a b & b^{2}+a^{2}
\end{array}\right]\)

= \(\left[\begin{array}{cc}
a^{2}+b^{2} & 0 \\
0 & a^{2}+b^{2}
\end{array}\right]\)

(ii) \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\left[\begin{array}{lll}
2 & 3 & 4
\end{array}\right]\) = \(\left[\begin{array}{lll}
1(2) & 1(3) & 1(4) \\
2(2) & 2(3) & 2(4) \\
3(2) & 3(3) & 3(4)
\end{array}\right]=\left[\begin{array}{ccc}
2 & 3 & 4 \\
4 & 6 & 8 \\
6 & 9 & 12
\end{array}\right]\)

(iii) \(\left[\begin{array}{cc}
1 & -2 \\
2 & 3
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & 3 \\
2 & 3 & 1
\end{array}\right]\) = \(\left[\begin{array}{lll}
1(1)-2(2) & 1(2)-2(3) & 1(3)-2(1) \\
2(1)+3(2) & 2(2)+3(3) & 2(3)+3(1)
\end{array}\right]\)

= \(\left[\begin{array}{lll}
1-4 & 2-6 & 3-2 \\
2+6 & 4+9 & 6+3
\end{array}\right]=\left[\begin{array}{ccc}
-3 & -4 & 1 \\
8 & 13 & 9
\end{array}\right]\)

(iv) \(\left[\begin{array}{lll}
2 & 3 & 4 \\
3 & 4 & 5 \\
4 & 5 & 6
\end{array}\right]\left[\begin{array}{ccc}
1 & -3 & 5 \\
0 & 2 & 4 \\
3 & 0 & 5
\end{array}\right]\) =

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 1

(v) \(\left[\begin{array}{cc}
2 & 1 \\
3 & 2 \\
-1 & 1
\end{array}\right]\left[\begin{array}{ccc}
1 & 0 & 1 \\
-1 & 2 & 1
\end{array}\right]\) =

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 2

(vi) \(\left[\begin{array}{ccc}
3 & -1 & 3 \\
-1 & 0 & 2
\end{array}\right]\left[\begin{array}{cc}
2 & -3 \\
1 & 0 \\
3 & 1
\end{array}\right]\) =

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 3

Question 4.
If A = \(\left[\begin{array}{ccc}
1 & 2 & -3 \\
5 & 0 & 2 \\
1 & -1 & 1
\end{array}\right]\), B = \(\left[\begin{array}{ccc}
3 & -1 & 2 \\
4 & 2 & 5 \\
2 & 0 & 3
\end{array}\right]\) and C = \(\left[\begin{array}{ccc}
4 & 1 & 2 \\
0 & 3 & 2 \\
1 & -2 & 3
\end{array}\right]\) then compute (A + B) and (B – C). Also, verify that A + (B – C) = (A + B) – C.
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 4

(A + B) – C = \(\left[\begin{array}{ccc}
4 & 1 & -1 \\
9 & 2 & 7 \\
3 & -1 & 4
\end{array}\right]-\left[\begin{array}{ccc}
4 & 1 & 2 \\
0 & 3 & 2 \\
1 & -2 & 3
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
4-4 & 1-1 & -1-2 \\
9-0 & 2-3 & 7-2 \\
3-1 & -1-(-2) & 4-3
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
0 & 0 & -3 \\
9 & -1 & 5 \\
2 & 1 & 1
\end{array}\right]\)
Hence, verified that A + (B – C) = (A + B) – C.

Question 5.
If A = \(\left[\begin{array}{ccc}
\frac{2}{3} & 1 & \frac{5}{3} \\
\frac{1}{3} & \frac{2}{3} & \frac{4}{3} \\
\frac{7}{3} & 2 & \frac{2}{3}
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
\frac{2}{5} & \frac{3}{5} & 1 \\
\frac{1}{5} & \frac{2}{5} & \frac{4}{5} \\
\frac{7}{5} & \frac{6}{5} & \frac{2}{5}
\end{array}\right]\)
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 5

Question 6.
Simplify cos θ \(\left[\begin{array}{cc}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\) + sin θ \(\left[\begin{array}{cc}
\sin \theta & -\cos \theta \\
\cos \theta & \sin \theta
\end{array}\right]\).
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 6

Question 7.
Find X and Y, if
(i) X + Y = \(\left[\begin{array}{ll}
7 & 0 \\
2 & 5
\end{array}\right]\) and X – Y = \(\left[\begin{array}{ll}
\mathbf{3} & \mathbf{0} \\
\mathbf{0} & \mathbf{3}
\end{array}\right]\)

(ii) 2X + 3Y = \(\left[\begin{array}{ll}
2 & 3 \\
4 & 0
\end{array}\right]\) and 3X + 2Y = \(\left[\begin{array}{cc}
2 & -2 \\
-1 & 5
\end{array}\right]\).
Solution.

(i) PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 7

(ii) PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 8

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 9

Question 8.
Find X, if Y = \(\left[\begin{array}{ll}
3 & 2 \\
1 & 4
\end{array}\right]\) and 2X + Y = \(\left[\begin{array}{cc}
1 & 0 \\
-3 & 2
\end{array}\right]\).
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 10

Question 9.
Find x and y, if 2\(\left[\begin{array}{ll}
1 & 3 \\
0 & x
\end{array}\right]+\left[\begin{array}{ll}
y & 0 \\
1 & 2
\end{array}\right]=\left[\begin{array}{ll}
5 & 6 \\
1 & 8
\end{array}\right]\)
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 11

Question 10.
Solve the equation for x, y, z and t, if 2 \(\left[\begin{array}{cc}
x & z \\
y & t
\end{array}\right]+3\left[\begin{array}{cc}
1 & -1 \\
0 & 2
\end{array}\right]=3\left[\begin{array}{ll}
3 & 5 \\
4 & 6
\end{array}\right]\).
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 12

On comparing the corresponding elements of these two matrices, we have
2x + 3 = 9
⇒ 2x = 6
⇒ x = 3

2y = 12
⇒ y = 6

2z – 3 = 15
⇒ 2z = 12
⇒ z = 6

2t + 6 = 18
⇒ 2t = 12
⇒ t = 6
Hence x = 3, y=6, z = 6 and t = 6.

Question 11.
If x\(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\) + y\(\left[\begin{array}{r}
-1 \\
1
\end{array}\right]\) = \(\left[\begin{array}{c}
10 \\
5
\end{array}\right]\), then find the values of x and y.
Solution.
If, \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\) + y\(\left[\begin{array}{r}
-1 \\
1
\end{array}\right]\) = \(\left[\begin{array}{c}
10 \\
5
\end{array}\right]\)
⇒ \(\left[\begin{array}{l}
2 x \\
3 x
\end{array}\right]+\left[\begin{array}{c}
-y \\
y
\end{array}\right]=\left[\begin{array}{c}
10 \\
5
\end{array}\right]\)

⇒ \(\left[\begin{array}{l}
2 x-y \\
3 x+y
\end{array}\right]=\left[\begin{array}{c}
10 \\
5
\end{array}\right]\)

On comparing the corresponding elements of these two matrices, we get 2x – y = 10 and 3x + y = 5 ………….(ii)
On adding Eq. (i) and (ii), we get
5x = 15
⇒ x = 3
Now, 3x + y = 5
⇒ y = 5 – 3x
⇒ y = 5 – 9 = – 4
Hence, x = 3 and y = – 4.

Question 12.
Given 3 \(\left[\begin{array}{ll}
x & y \\
z & w
\end{array}\right]=\left[\begin{array}{cc}
x & 6 \\
-1 & 2 w
\end{array}\right]+\left[\begin{array}{cc}
4 & x+y \\
z+w & 3
\end{array}\right]\) find the values of x, y and z.
Solution.
Given, 3 \(\left[\begin{array}{ll}
x & y \\
z & w
\end{array}\right]=\left[\begin{array}{cc}
x & 6 \\
-1 & 2 w
\end{array}\right]+\left[\begin{array}{cc}
4 & x+y \\
z+w & 3
\end{array}\right]\)

⇒ \(\left[\begin{array}{ll}
3 x & 3 y \\
3 z & 3 w
\end{array}\right]=\left[\begin{array}{cc}
x+4 & 6+x+y \\
-1+z+w & 2 w+3
\end{array}\right]\)

On comparing the corresponding elements of these two matrices, we get
3x = x + 4
⇒ 2x = 4
⇒ x = 2
and 3y = 6 + x + y
⇒ 2y = 6 + x
⇒ 2y = 6+ 2
⇒ 2y = 8
⇒ y = 4
3w = 2w + 3
⇒ w = 3
3z = – 1 + z + w
⇒ 2z = – 1 + w = – 1 + 3 = 2
⇒ z = 1
Hence, x = 2, y = 4, z = 1, and w = 3.

Question 13.
If F(x) = \(\left[\begin{array}{ccc}
\cos x & -\sin x & 0 \\
\sin x & \cos x & 0 \\
0 & 0 & 1
\end{array}\right]\), show that F(x) F(y) = F(x + y).
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 13

Question 14.
Show that
(i) \(\left[\begin{array}{cc}
5 & -1 \\
6 & 7
\end{array}\right]\left[\begin{array}{cc}
2 & 1 \\
3 & 4
\end{array}\right] \neq\left[\begin{array}{cc}
2 & 1 \\
3 & 4
\end{array}\right]\left[\begin{array}{cc}
5 & -1 \\
6 & 7
\end{array}\right]\)

(ii) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 1 & 0 \\
1 & 1 & 0
\end{array}\right]\left[\begin{array}{ccc}
-1 & 1 & 0 \\
0 & -1 & 1 \\
2 & 3 & 4
\end{array}\right] \neq\left[\begin{array}{ccc}
-1 & 1 & 0 \\
0 & -1 & 1 \\
2 & 3 & 4
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 1 & 0 \\
1 & 1 & 0
\end{array}\right]\)
Solution.
(i) PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 14

(ii) PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 15

Question 15.
Find A² – 5A + 6I, if A = \(\left[\begin{array}{ccc}
\mathbf{2} & \mathbf{0} & \mathbf{1} \\
\mathbf{2} & \mathbf{1} & \mathbf{3} \\
\mathbf{1} & -\mathbf{1} & \mathbf{0}
\end{array}\right]\).
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 16

Question 16.
If A = \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\), prove that A³ – 6A² + 7A + 2I = 0.
Solution.
A² = A . A
= \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\)

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 17

Question 17.
If A = \(\left[\begin{array}{ll}
3 & -2 \\
4 & -2
\end{array}\right]\) and I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\), find k so that A² = kA – 2I
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 18

⇒ \(\left[\begin{array}{ll}
1 & -2 \\
4 & -4
\end{array}\right]=\left[\begin{array}{cc}
3 k-2 & -2 k \\
4 k & -2 k-2
\end{array}\right]\)
On comparing the corresponding elements, we get
3k – 2 = 1
⇒ 3k = 3
⇒ k = 1
Thus, the value of k is 1.

Question 18.
If A = \(\left[\begin{array}{cc}
0 & -\tan \frac{\alpha}{2} \\
\tan \frac{\alpha}{2} & 0
\end{array}\right]\) and I is the identity matrix of order 2, show that I + A = (I – A) \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\).
Solution.

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 19

PSEB 12th Class Maths Solutions Chapter 3 Matrices Ex 3.2 20

Thus, from Eqs. (i) and (ii), we get L.H.S = R.H.S.

Question 19.
A trust fund has ₹ 30000 that must be invested in two different types of bonds. The first bond pays 5 % interest per year, and the second bond pays 7 % interest per year. Using matrix multiplication, determine how to divide ₹ 30000 among the two types of bonds. If the trust fund must obtain an annual total interest of:
(a) ₹ 1800
(b) ₹ 2000
Solution.
(a) Let ₹ x be invested in the first bond. Then, the sum of money invested in the second bond will be ₹ (30000 – x).
It is given that the first bond pays 5% interest per year and the second bond pays 7% interest per year.
Therefore, in order to obtain an annual total interest of ₹ 1800, we have
⇒ 2x = 30000
⇒ x = 15000
Thus, in order to obtain an annual total interest of ₹ 1800, the trust fund should invest ₹ 15000 in the first bond and the remaining ?15000 in the second bond.

(b) Let ₹ x be invested in the first bond. Then, the sum of money invested in the second bond will be ₹ (30000 – x).
Therefore, in order to obtain an annual total interest of ₹ 2000, we have
[x (30000 – x)] \(\left[\begin{array}{c}
\frac{5}{100} \\
\frac{7}{100}
\end{array}\right]\) = [2000]

⇒ \(\frac{5 x}{100}+\frac{7(30000-x)}{100}\) = [2000]
⇒ 5x + 210000 – 7x = 200000
⇒ 210000 – 2x = 200000
⇒ 2x = 210000 – 200000
⇒ 2x = 10000
⇒ x = 5000
Thus, in order to obtain an annual total interest of ?2000, the trust fund should invest ₹ 5000 in the first bond and the remaining ₹ 25000 in the second bond.

Question 20.
The bookshop of a particular school has 10 dozen Chemistry books, 8 dozen Physics books and 10 dozen Economics books. Their selling prices are ₹ 80, ₹ 60, and ₹ 40 each respectively. Find the total amount the bookshop will receive from selling all the books using matrix algebra.
Solution.
The bookshop has 10 dozen Chemistry books, 8 dozen Physics book and 10 dozen Economics books.
The selling prices of a Chemistry book, a Physics book and an Economics book are respectively given as ₹ 80, ₹ 60 and ₹ 40.
The total amount of money that will be received from the sale of all,these books can be represented in the form of a matrix as
12 [10 8 10] \(\left[\begin{array}{l}
80 \\
60 \\
40
\end{array}\right]\)
= 12[10 × 80 + 8 × 60 + 10 × 40]
= 12 [800 + 480 + 400]
= 12(1680) = 20160
Thus, the bookshop will receive ₹ 20160 from the sale of all these books.

Direction (21 – 22)
Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3, and p × k, respectively. Choose the correct answer in Q. 21 and Q. 22.

Question 21.
The restrictions on n, k and p so that PY + WY will be defined, are
(A) k – 3, p = n
(B) k is arbitrary, p = 2
(C) p is arbitrary, k – 3
(D) k = 2, p = 3
Solution.
Matrices P and Y are of the orders p × k and 3 × k, respectively.
Therefore, matrix PY will be defined if k – 3. Consequently, PY will be of the order p × k.
Matrices W and Y are of the orders n × 3 and 3 × k, respectively.
Since, the number of columns in W is equal to the number of rows in Y, matrix WY is well-defined and is of the order n × k.
Matrices PY and WY can be added only when their orders are the same. However, PY is of the order p × k and WY is of the order n × k. Therefore, we must have p = n.
Thus, k = 3 and p = n are the restrictions on n, k and p so that PY + WY will be defined.
Hence, the correct answer is (A).

Question 22.
If n = p, then the order of the matrix IX – 5Z is
(A) p × 2
(B) 2 × n
(C) C n × 3
(D) p × n
Solution.
Matrix X is of the order 2 × n.
Therefore, matrix 7X is also of the same order.
Matrix Z is of the order 2 × p,i.e., 2 × n [∵ n = p]
Therefore, matrix 5Z is also of the same order.
Now, both the matrices 7X and 5Z are of the order 2 × n.
Thus, matrix 7X – 5Z is well-defined and is of the order 2 × n.
Hence, the correct answer is (B).