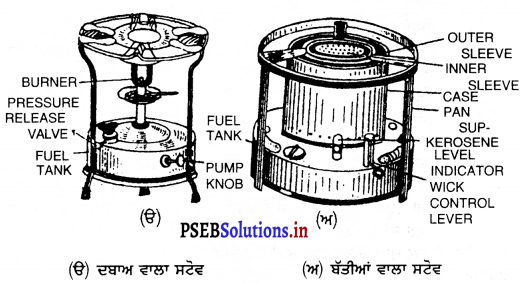
Punjab State Board PSEB 9th Class Home Science Book Solutions Chapter 6 ਰਸੋਈ ਦਾ ਪ੍ਰਬੰਧ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Home Science Chapter 6 ਰਸੋਈ ਦਾ ਪ੍ਰਬੰਧ
Home Science Guide for Class 9 PSEB ਰਸੋਈ ਦਾ ਪ੍ਰਬੰਧ Textbook Questions and Answers
ਪਾਠ-ਪੁਸਤਕ ਦੇ ਪ੍ਰਸ਼ਨ ਉੱਤਰ
ਵਸਤੁਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਰਸੋਈ ਘਰ ਦਾ ਮਹੱਤਵਪੂਰਨ ਹਿੱਸਾ ਕਿਉਂ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਰਸੋਈ ਵਿਚ ਘਰ ਦੇ ਮੈਂਬਰਾਂ ਲਈ ਖਾਣਾ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਤੇ ਗਹਿਣੀ ਦਾ ਮੁੱਖ ਕੰਮ ਰਸੋਈ ਵਿਚ ਹੀ ਹੁੰਦਾ ਹੈ ਤੇ ਉਸ ਦਾ ਜ਼ਿਆਦਾ ਸਮਾਂ ਰਸੋਈ ਵਿਚ ਹੀ ਬੀਤਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਰਸੋਈ ਘਰ ਦਾ ਮਹੱਤਵਪੂਰਨ ਹਿੱਸਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਪੁਰਾਣੀ ਕਿਸਮ ਅਤੇ ਨਵੀਂ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਮੁੱਖ ਅੰਤਰ ਕੀ ਹੈ?
ਉੱਤਰ-
ਪੁਰਾਣੀ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਸਾਰਾ ਕੰਮ ਜ਼ਮੀਨ ਤੇ ਬੈਠ ਕੇ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਜਿਵੇਂ ਖਾਣਾ ਪਕਾਉਣਾ ਤੇ ਖਾਣਾ ਖਾਣ ਲਈ ਵੀ ਪਟੜੇ ਜਾਂ ਪੀੜੀ ਤੇ ਹੀ ਬੈਠਿਆ ਜਾਂਦਾ ਸੀ । . ਨਵੀਂ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਸਾਰਾ ਕੰਮ ਖੜੇ ਹੋ ਕੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਤੇ ਬਾਰ-ਬਾਰ ਉੱਠਣ ਬੈਠਣ ਲਈ ਸਮਾਂ ਤੇ ਸ਼ਕਤੀ ਖ਼ਰਾਬ ਨਹੀਂ ਹੁੰਦੀ । ਫਰਿਜ਼ ਵਗੈਰਾ ਵੀ ਰਸੋਈ ਵਿਚ ਹੀ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਰਸੋਈ ਦੇ ਕੰਮ ਨੂੰ ਕਿਨ੍ਹਾਂ ਕਾਰਜ ਖੇਤਰਾਂ ਵਿਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ?
ਉੱਤਰ-
ਰਸੋਈ ਘਰ ਵਿਚ ਕਿਸ ਤਰ੍ਹਾਂ ਕੰਮ ਕੀਤਾ ਜਾਵੇ ਅਰਥਾਤ ਵੱਖ-ਵੱਖ ਕਾਰਜਾਂ ਦੇ ਪ੍ਰਬੰਧ ਨੂੰ ਕਾਰਜ ਵਿਵਸਥਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਰਸੋਈ ਦੇ ਕੰਮ ਨੂੰ ਤਿੰਨ ਕਾਰਜ ਖੇਤਰਾਂ ਵਿਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ।
- ਭੋਜਨ ਦੀ ਤਿਆਰੀ
- ਪਕਾਉਣਾ ਤੇ ਵਰਤਾਉਣਾ
- ਹੁੰਦੀ ।
ਪ੍ਰਸ਼ਨ 4.
ਨਵੀਂ ਕਿਸਮ ਦੀਆਂ ਰਸੋਈਆਂ ਕਿਹੜੀ-ਕਿਹੜੀ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਨਵੀਂ ਰਸੋਈ ਵਿਚ ਖੜ੍ਹੇ ਹੋ ਕੇ ਕੰਮ ਕਰਨ ਲਈ ਸ਼ੈਲਫਾਂ ਹੁੰਦੀਆਂ ਹਨ । ਸ਼ੈਲਫ ਦੇ ਅਨੁਸਾਰ ਪੰਜ ਕਿਸਮ ਦੀਆਂ ਰਸੋਈਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
- ਇਕ ਦੀਵਾਰ ਵਾਲੀ
- ਦੋ ਦੀਵਾਰਾਂ ਵਾਲੀ
- ਐਲ (L) ਸ਼ਕਲ ਵਾਲੀ .
- ਯੂ (U) ਸ਼ਕਲ ਵਾਲੀ ਅਤੇ
- ਟੁੱਟਿਆ ਯੂ (U) ਸ਼ਕਲ ਵਾਲੀ ।
ਪ੍ਰਸ਼ਨ 5.
ਰਸੋਈ ਵਿਚ ਬਿਜਲੀ ਦੇ ਸਵਿਚ ਕਿੰਨੇ ਕੁ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਰਸੋਈ ਵਿਚ ਬਿਜਲੀ ਦੇ ਉਪਕਰਨਾਂ ਦੀ ਵਰਤੋਂ ਦੇ ਹਿਸਾਬ ਨਾਲ ਸਵਿਚ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਬੇਲੋੜੇ ਵਿਚ ਨਹੀਂ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਰਸੋਈ ਦਾ ਰੰਗ ਕਿਹੋ ਜਿਹਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਕਿਉਂ ?
ਉੱਤਰ-
ਰਸੋਈ ਵਿਚ ਹਲਕੇ ਰੰਗਾਂ ਦਾ ਇਸਤੇਮਾਲ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਕਿਉਂਕਿ ਹਲਕੇ ਰੰਗ ਖੁੱਲ੍ਹੇਪਣ ਦਾ ਅਹਿਸਾਸ ਕਰਵਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 7.
ਰਸੋਈ ਨਾਲ ਸਟੋਰ ਦੀ ਜ਼ਰੂਰਤ ਕਦੋਂ ਅਤੇ ਕਿਉਂ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਜਿਹੜੇ ਘਰਾਂ ਵਿਚ ਰਸੋਈ ਦਾ ਸਾਮਾਨ ਇਕੱਠਾ ਖ਼ਰੀਦਿਆ ਜਾਂਦਾ ਹੈ ਉਹਨਾਂ ਘਰਾਂ ਵਿਚ ਰਸੋਈ ਦੇ ਨਾਲ ਸਟੋਰ ਵੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਮੱਖੀ ਮੱਛਰ ਤੋਂ ਬਚਣ ਲਈ ਤੁਸੀਂ ਰਸੋਈ ਵਿਚ ਕੀ ਉਪਬੰਧ ਕਰੋਗੇ ?
ਉੱਤਰ-ਮੱਛਰ ਮੱਖੀ ਤੋਂ ਬਚਾਅ ਲਈ ਰਸੋਈ ਦੇ ਦਰਵਾਜ਼ਿਆਂ ਅਤੇ ਖਿੜਕੀਆਂ ਤੇ ਜਾਲੀ ਲੱਗੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਜਾਲੀ ਦੇ ਦਰਵਾਜ਼ੇ ਹਮੇਸ਼ਾਂ ਬੰਦ ਰੱਖਣੇ ਚਾਹੀਦੇ ਹਨ । ਰਸੋਈ ਸਾਫ਼ ਸੁਥਰੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਰਸੋਈ ਦੀ ਸਫ਼ਾਈ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਰਸੋਈ ਦੀ ਸਾਫ਼-ਸਫ਼ਾਈ ਇਸ ਲਈ ਜ਼ਰੂਰੀ ਹੈ ਕਿਉਂਕਿ ਜੇ ਰਸੋਈ ਗੰਦੀ ਹੋਵੇ ਤਾਂ ਕਈ ਜੀਵ ਜੰਤੂਆਂ ਨੂੰ ਆਪਣਾ ਘਰ ਬਣਾਉਣ ਦਾ ਮੌਕਾ ਮਿਲ ਜਾਵੇਗਾ ਕਿਉਂਕਿ ਰਸੋਈ ਵਿਚ ਖਾਧ-ਪਦਾਰਥ ਉਹਨਾਂ ਨੂੰ ਆਸਾਨੀ ਨਾਲ ਉਪਲੱਬਧ ਹੋ ਸਕਦੇ ਹਨ । ਰਸੋਈ ਦਾ ਪ੍ਰਬੰਧ ‘ ਰਸੋਈ ਵਿਚ ਜ਼ਹਿਰੀਲੀਆਂ ਦਵਾਈਆਂ ਦੀ ਵਰਤੋਂ ਵੀ ਨਹੀਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਇਸ ਲਈ ਇਹ ਅਤਿ ਜ਼ਰੂਰੀ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿ ਰਸੋਈ ਦੀ ਸਫ਼ਾਈ ਦਾ ਖ਼ਾਸ ਖ਼ਿਆਲ ਰੱਖਿਆ ਜਾਵੇ ।
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 10.
ਘਰ ਵਿਚ ਰਸੋਈ ਦੀ ਚੋਣ ਕਿਵੇਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
- ਰਸੋਈ ਦੀ ਚੋਣ ਘਰ ਅਤੇ ਘਰ ਵਾਲਿਆਂ ਦੀ ਗਿਣਤੀ ਅਨੁਸਾਰ ਕੀਤੀ ਜਾਣੀ ਚਾਹੀਦੀ ਹੈ ।
- ਰਸੋਈ ਅਜਿਹੀ ਥਾਂ ਤੇ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਜਿੱਥੇ ਹਵਾ ਅਤੇ ਸਿੱਧੀ ਰੋਸ਼ਨੀ ਪਹੁੰਚ ਸਕੇ ।
- ਦਰਵਾਜ਼ੇ ਅਤੇ ਖਿੜਕੀਆਂ ਹਵਾ ਦੀ ਦਿਸ਼ਾ ਵਿਚ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ।
- ਰਸੋਈ ਵਿਚ ਅੱਗ ਦੀ ਗਰਮੀ ਹੁੰਦੀ ਹੈ ਇਸ ਲਈ ਰਸੋਈ ਵਿਚ ਧੁੱਪ ਨਹੀਂ ਆਉਣੀ ਚਾਹੀਦੀ । ਨਹੀਂ ਤਾਂ ਗਰਮੀਆਂ ਵਿੱਚ ਰਸੋਈ ਜ਼ਿਆਦਾ ਗਰਮ ਹੋ ਜਾਵੇਗੀ ।
- ਰਸੋਈ ਨਾ ਤਾਂ ਬਹੁਤੀ ਵੱਡੀ ਹੋਵੇ ਤੇ ਨਾ ਹੀ ਬਹੁਤੀ ਛੋਟੀ । ਛੋਟੀ ਰਸੋਈ ਵਿਚ ਕੰਮ ਕਰਨਾ ਔਖਾ ਹੋ ਜਾਂਦਾ ਹੈ ਤੇ ਜ਼ਿਆਦਾ ਵੱਡੀ ਰਸੋਈ ਵਿਚ ਜ਼ਿਆਦਾ ਮਿਹਨਤ ਕਰਨੀ ਪੈਂਦੀ ਹੈ ।
- ਰਸੋਈ ਨੂੰ ਸ਼ੌਚਾਲਯ ਅਤੇ ਨਾਲੀਆਂ ਤੋਂ ਦੂਰ ਬਣਾਉ ਤਾਂ ਕਿ ਇਹਨਾਂ ਵਿਚਲੀ ਦੁਰਗੰਧ ਰਸੋਈ ਤਕ ਨਾ ਪਹੁੰਚ ਸਕੇ ।
![]()
ਪ੍ਰਸ਼ਨ 11.
ਰਸੋਈ ਘਰ ਦਾ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਹਿੱਸਾ ਹੈ । ਇਸ ਤੱਥ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਮਨੁੱਖ ਕੰਮ ਕਾਜ ਕਰਨ ਲਈ ਊਰਜਾ ਭੋਜਨ ਤੋਂ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ਤੇ ਭੋਜਨ ਰਸੋਈ ਘਰ ਵਿਚ ਪਕਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਰਸੋਈ ਦਾ ਮਨੁੱਖ ਦੇ ਜੀਵਨ ਵਿਚ ਕਾਫ਼ੀ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਹੈ । ਹਿਣੀ ਰਸੋਈ ਦੀ ਮਾਲਕਣ ਹੁੰਦੀ ਹੈ, ਉਸ ਦਾ ਕਾਫ਼ੀ ਸਮਾਂ ਰਸੋਈ ਵਿਚ ਹੀ ਬੀਤਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਰਸੋਈ ਘਰ ਦਾ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਹਿੱਸਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਰਸੋਈ ਵਿਚ ਕੰਮ ਕਰਨ ਦੇ ਮੁੱਖ ਕੇਂਦਰ ਕਿਹੜੇ ਹਨ ਅਤੇ ਇੱਥੇ ਕੀ-ਕੀ ਕੰਮ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਰਸੋਈ ਵਿਚ ਕੰਮ ਕਰਨ ਦੇ ਤਿੰਨ ਮੁੱਖ ਕੇਂਦਰ ਹਨ-
- ਭੋਜਨ ਦੀ ਤਿਆਰੀ,
- ਭੋਜਨ ਪਕਾਉਣਾ ਤੇ ਵਰਤਾਉਣਾ ਅਤੇ
- ਹੁੰਦੀ ।
1. ਭੋਜਨ ਦੀ ਤਿਆਰੀ – ਭੋਜਨ ਪਕਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਸਬਜ਼ੀਆਂ ਨੂੰ ਛਿੱਲਣ, ਕੱਟਣ, ਚੁਣਨ ਆਦਿ ਦੀ ਤਿਆਰੀ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਖਾਣਾ ਪਕਾਉਣ ਲਈ ਹੋਰ ਸੰਬੰਧਤ ਕਾਰਜ ਵੀ ਇੱਥੇ ਹੀ ਹੁੰਦੇ ਹਨ । ਇਸ ਲਈ ਰਸੋਈ ਖੁੱਲ੍ਹੀ-ਡੁੱਲ੍ਹੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਸਮਾਂ ਅਤੇ ਸ਼ਕਤੀ ਬਚਾਉਣ ਲਈ ਹੁੰਦੀ ਅਤੇ ਖਾਣਾ ਪਕਾਉਣ ਵਾਲੀ ਜਗ੍ਹਾ ਨੇੜੇ-ਨੇੜੇ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ਅਤੇ ਰੈਫਰੀਜ਼ਰੇਟਰ ਦਾ ਦਰਵਾਜ਼ਾ ਜਿਸ ਪਾਸੇ ਖੁੱਲ੍ਹਦਾ ਹੋਵੇ ਕਾਊਂਟਰ (ਸ਼ੈਲਫ) ਵੀ ਉਸੇ ਪਾਸੇ ਹੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
2. ਭੋਜਨ ਪਕਾਉਣ ਅਤੇ ਵਰਤਾਉਣ ਵਾਲੀ ਥਾਂ – ਰਸੋਈ ਦੇ ਇਸ ਹਿੱਸੇ ਵਿਚ ਖਾਣਾ ਪਕਾ ਕੇ ਗਰਮ ਗਰਮ ਵਰਤਾਇਆ ਜਾਂਦਾ ਹੈ । ਇੱਥੇ ਬਿਜਲੀ ਦਾ ਚੁੱਲਾ, ਗੈਸ, ਸਟੋਵ ਜਾਂ ਅੰਗੀਠੀ ਆਦਿ ਰੱਖਿਆ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਦੇ ਆਲੇ-ਦੁਆਲੇ ਜਗਾ ਖੁੱਲ੍ਹੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਤਾਂ ਜੋ ਖਾਣਾ ਪਕਾਉਣ ਵੇਲੇ ਸੌਖ ਰਹੇ | ਖਾਣਾ ਪਕਾਉਣ ਵਾਲੇ ਬਰਤਨ ਇਸ ਜਗਾ ਦੇ ਨੇੜੇ ਹੀ ਸ਼ੈਲਫ਼ ਪਾ ਕੇ ਰੱਖਣ ਦੀ ਜਗ੍ਹਾ ਬਣਾ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ । ਕੜਛੀਆਂ ਅਤੇ ਚਮਚ ਆਦਿ ਟੰਗਣ ਲਈ ਵੀ ਖੁੰਟੀਆਂ ਲੱਗੀਆਂ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ।
3. ਹੁੰਦੀ – ਹੌਦੀ ਦੀ ਵਰਤੋਂ ਆਮ ਤੌਰ ‘ਤੇ ਬਰਤਨ ਸਾਫ਼ ਕਰਨ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਰੈਫਰੀਜ਼ਰੇਟਰ ਵਿਚ ਭੋਜਨ ਪਦਾਰਥ ਰੱਖਣ ਤੋਂ ਪਹਿਲਾਂ ਉਹਨਾਂ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਧੋਣ ਲਈ ਵੀ ਹੁੰਦੀ ਦੀ ਵਰਤੋਂ ਹੁੰਦੀ ਹੈ | ਖਾਣਾ ਪਕਾਉਣ ਅਤੇ ਇਸ ਦੀ ਤਿਆਰੀ ਵੇਲੇ ਵੀ ਪਾਣੀ ਇੱਥੇ ਲੱਗੀ ਟੂਟੀ ਤੋਂ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਲਈ ਰਸੋਈ ਵਿਚ ਹੁੰਦੀ ਸੌਖੀ ਪਹੁੰਚ ਅੰਦਰ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ, ਖੂੰਜੇ ਵਿਚ ਨਹੀਂ । ਹੌਦੀ ਦੇ ਨੇੜੇ ਬਰਤਨ ਤੇ ਲੋੜੀਂਦਾ ਸਮਾਨ ਰੱਖਣ ਦੀ ਥਾਂ ਵੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਆਸੇ ਪਾਸੇ ਦਾ ਪਾਣੀ ਨੁਚੜ ਕੇ ਹਿੰਦੀ ਵਿਚ ਹੀ ਪੈਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 13.
ਰਸੋਈ ਦੀ ਬਣਤਰ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ? ਨਵੀਂ ਅਤੇ ਪੁਰਾਣੀ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਕੀ ਅੰਤਰ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਰਸੋਈ ਦੇ ਦਰਵਾਜ਼ੇ ਅਤੇ ਖਿੜਕੀਆਂ ‘ਤੇ ਜਾਲੀ ਲੱਗੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਤੇ ਇਹਨਾਂ ਦਰਵਾਜ਼ਿਆਂ ਨੂੰ ਹਮੇਸ਼ਾ ਬੰਦ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਮੱਖੀ ਮੱਛਰ ਰਸੋਈ ਵਿਚ ਨਹੀਂ ਵੜ ਸਕੇਗਾ | ਰਸੋਈ ਵਿਚ ਰੋਸ਼ਨਦਾਨਾਂ ਦਾ ਹੋਣਾ ਲਾਜ਼ਮੀ ਹੈ । | ਰਸੋਈ ਦਾ ਧੂੰਆਂ ਕੱਢਣ ਲਈ ਚਿਮਨੀ ਜਾਂ ਐਗਜ਼ਾਸਟ ਪੱਖਾ ਲੱਗਾ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ । ਆਮ ਪਰਿਵਾਰ ਲਈ ਰਸੋਈ ਦਾ ਆਕਾਰ 9′ × 10’ ਫੁੱਟ ਦਾ ਹੁੰਦਾ ਹੈ । ਪਰ ਇਹ ਘਰ ਦੇ ਆਕਾਰ ਦੇ ਅਨੁਸਾਰ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ।
ਨਵੀਂ ਅਤੇ ਪੁਰਾਣੀ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਅੰਤਰ-ਪੁਰਾਣੇ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਜ਼ਮੀਨ ਤੇ ਬੈਠ ਕੇ ਹੀ ਸਾਰਾ ਕੰਮ ਕੀਤਾ ਜਾਂਦਾ ਹੈ | ਪਰ ਨਵੇਂ ਕਿਸਮ ਦੀਆਂ ਰਸੋਈਆਂ ਵਿਚ ਖੜੇ ਹੋ ਕੇ ਸਾਰਾ ਕੰਮ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਲਈ ਸ਼ੈਲਫ਼ਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਸ਼ੈਲਫ਼ਾਂ ਦੀ ਉਚਾਈ ਆਮ ਕਰਕੇ ਫ਼ਰਸ਼ ਤੋਂ 21/2 ਫੁੱਟ ਹੁੰਦੀ ਹੈ ਪਰ ਤ੍ਰਿਣੀ ਦੀ ਲੰਬਾਈ ਮੁਤਾਬਿਕ ਇਹ ਉਚਾਈ ਵੱਧ-ਘੱਟ ਵੀ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 14.
ਨਵੀਂ ਕਿਸਮ ਦੀਆਂ ਤਿੰਨ ਰਸੋਈਆਂ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਰਸੋਈ ਵਿਚ ਪਾਈ ਜਾਣ ਵਾਲੀ ਸ਼ੈਲਫ਼ ਦੇ ਅਨੁਸਾਰ ਰਸੋਈਆਂ ਪੰਜ ਤਰ੍ਹਾਂ ਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚੋਂ ਤਿੰਨਾਂ ਦਾ ਵੇਰਵਾ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ
1. ਐੱਲ ਸ਼ਕਲ (L) ਦੀ ਰਸੋਈ – ਆਮ ਘਰਾਂ ਵਿਚ (L) ਸ਼ਕਲ ਦੀ ਰਸੋਈ ਹੀ ਪ੍ਰਚਲਿਤ ਹੈ ।ਇਕ ਬਾਹੀ ਲੰਬੀ ਅਤੇ ਦੂਸਰੀ ਛੋਟੀ ਹੁੰਦੀ ਹੈ । ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਆਮ ਤੌਰ ‘ਤੇ ਲੰਬੇ ਪਾਸੇ ਕੰਮ ਕਰਨ ਦੇ ਦੋ ਕੇਂਦਰ ਜਿਵੇਂ ਹੁੰਦੀ ਅਤੇ ਤਿਆਰੀ ਦਾ ਕੇਂਦਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਛੋਟੀ ਬਾਹੀ ਵਾਲੇ ਪਾਸੇ ਖਾਣਾ ਪਕਾਉਣ ਦਾ ਕੇਂਦਰ ਹੁੰਦਾ ਹੈ ।
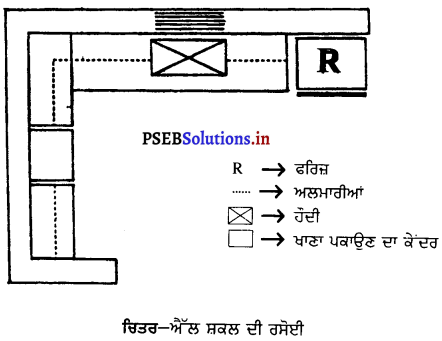
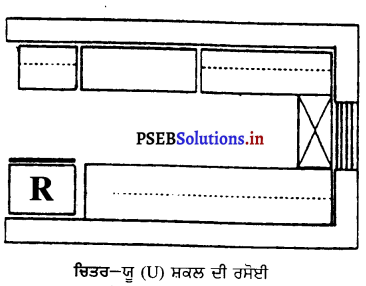
2. ਯੂ (U) ਸ਼ਕਲ ਦੀ ਰਸੋਈ – ਰਸੋਈਆਂ ਵਿਚੋਂ ਯੂ ਕਿਸਮ ਦੀ ਰਸੋਈ ਸਾਰੀਆਂ ਕਿਸਮਾਂ ਤੋਂ ਚੰਗੀ ਮੰਨੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਇਹ ਕਾਫ਼ੀ ਪ੍ਰਚਲਿਤ ਵੀ ਹੈ । ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਖਾਣਾ ਪਕਾਉਣ ਦਾ ਕੇਂਦਰ ਇਕ ਬਾਹੀ ਦੇ ਦਰਮਿਆਨ ਹੁੰਦਾ ਹੈ ਅਤੇ ਦੂਸਰੀ ਬਾਹੀ ਤਿਆਰੀ ਦੇ ਕੇਂਦਰ ਵਜੋਂ ਵਰਤੀ ਜਾਂਦੀ ਹੈ । ਹੌਦੀ ਯੂ ਦੇ ਤਲ ਤੇ ਹੋ ਸਕਦੀ ਹੈ । ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਕੰਮ ਕਰਨ ਲਈ ਅਤੇ ਸਮਾਨ ਰੱਖਣ ਲਈ ਅਲਮਾਰੀਆਂ ਬਣਾਉਣ ਲਈ ਕਾਫ਼ੀ ਥਾਂ ਹੁੰਦੀ ਹੈ । ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਜ਼ਿਆਦਾ ਤੁਰਨਾ-ਫਿਰਨਾ ਨਹੀਂ ਪੈਂਦਾ ਅਤੇ ਰਸੋਈ ਲਾਂਘਾ ਵੀ ਨਹੀਂ ਬਣਦੀ ।
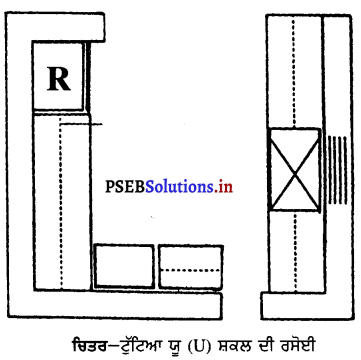
3. ਟੁੱਟਿਆ ਧੂ (U) ਸ਼ਕਲ ਦੀ ਰਸੋਈ – ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਯੂ (U) ਦੇ ਤਲ ਵਾਲੇ ਪਾਸੇ ਸ਼ੈਲਫ ਪੂਰੀ ਨਹੀਂ ਹੁੰਦੀ ਪਰ ਯੂ ਸ਼ਕਲ ਦੀ ਰਸੋਈ ਵਾਂਗ ਇਸ ਵਿਚ ਵੀ ਕੰਮ ਕਰਨ ਲਈ ਅਤੇ ਸਮਾਨ ਰੱਖਣ ਲਈ ਕਾਫ਼ੀ ਥਾਂ ਹੁੰਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 15.
ਰਸੋਈ ਦਾ ਸਾਜੋ ਸਮਾਨ ਰੱਖਣ ਲਈ ਕੀ-ਕੀ ਉਪਬੰਧ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਰਸੋਈ ਵਿਚ ਸਮਾਨ ਰੱਖਣ ਲਈ ਦੀਵਾਰਾਂ ਵਿਚ ਅਲਮਾਰੀਆਂ ਜਾਂ ਰੈਕ ਬਣਾਏ ਹੁੰਦੇ ਹਨ ।
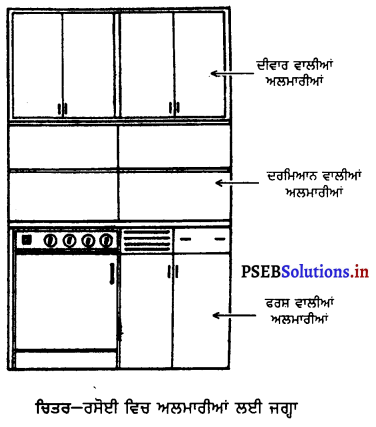
ਅਲਮਾਰੀਆਂ ਆਪਣੀ ਜ਼ਰੂਰਤ ਅਨੁਸਾਰ ਘੱਟ ਜਾਂ ਵੱਧ ਬਣਾਈਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ । ਸ਼ੈਲਫਾਂ, ਰੈਕ ਜਾਂ ਅਲਮਾਰੀਆਂ ਕੰਮ ਕਰਨ ਦੇ ਹਰੇਕ ਕੇਂਦਰ ਜਿਵੇਂ ਭੋਜਨ ਦੀ ਤਿਆਰੀ, ਪਕਾਉਣ ਦਾ ਕੇਂਦਰ ਅਤੇ ਹੌਦੀ ਅਨੁਸਾਰ ਹੀ ਬਣਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਰਸੋਈ ਵਿਚ ਬਰਤਨ ਰੱਖਣ ਲਈ ਐਲੂਮੀਨੀਅਮ ਜਾਂ ਸਟੀਲ ਦੇ ਸਟੈਂਡ ਵੀ ਲਏ ਜਾ ਸਕਦੇ ਹਨ । ਇਹ ਦੀਵਾਰ ਵਿਚ ਵੀ ਫਿਟ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਪਲੇਟਾਂ, ਕਟੋਰੀਆਂ, ਗਿਲਾਸ, ਡੂੰਗੇ ਆਦਿ ਰੱਖਣ ਲਈ ਵੱਖਰੀ-ਵੱਖਰੀ ਥਾਂ ਹੁੰਦੀ ਹੈ ।
ਵਸਤੂਆਂ ਨੂੰ ਰੈਫਰੀਜਰੇਟਰ ਜਾਂ ਜਾਲੀਦਾਰ ਅਲਮਾਰੀ ਵਿਚ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਕੋਈ ਵੀ ਵਸਤੁ ਨੰਗੀ ਨਹੀਂ ਰੱਖਣੀ ਚਾਹੀਦੀ ।
ਪ੍ਰਸ਼ਨ 16.
ਰਸੋਈ ਦੀ ਯੋਜਨਾ ਬਣਾਉਂਦੇ ਸਮੇਂ ਕਿਨ੍ਹਾਂ ਗੱਲਾਂ ਨੂੰ ਧਿਆਨ ਵਿਚ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ? .
ਉੱਤਰ-
ਰਸੋਈ ਦੀ ਯੋਜਨਾ ਬਣਾਉਣ ਵੇਲੇ ਵਿਚਾਰਨ ਵਾਲੀਆਂ ਗੱਲਾਂ ਇਸ ਤਰ੍ਹਾਂ ਹਨ-
- ਪਾਣੀ ਲਈ ਹਿੰਦੀ ਵਿਚ ਟੁਟੀ ਦਾ ਪ੍ਰਬੰਧ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਜਾਂ ਫਿਰ ਕਿਸੇ ਬਾਲਟੀ ਆਦਿ ਨੂੰ ਟੂਟੀ ਲਾ ਕੇ ਪਾਣੀ ਨਾਲ ਭਰ ਕੇ ਰੱਖ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਰਸੋਈ ਵਿਚ ਸਮਾਨ ਰੱਖਣ ਲਈ ਅਲਮਾਰੀਆਂ, ਰੈਕ ਆਦਿ ਤੇ ਕੜਛੀਆਂ, ਚਮਚੇ, ਚਾਕੂ ਆਦਿ ਟੰਗਣ ਲਈ ਖੁੰਟੀਆਂ ਆਦਿ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ।
- ਰਸੋਈ ਦਾ ਫਰਸ਼ ਪੱਕਾ ਸੰਗਮਰਮਰ, ਰੰਗਦਾਰ ਟਾਇਲਾ, ਲਿਨੋਲੀਅਮ ਆਦਿ ਦਾ ਅਤੇ ਜਲਦੀ ਸਾਫ਼ ਹੋ ਸਕਣ ਵਾਲਾ ਅਤੇ ਜ਼ਿਆਦਾ ਢਲਾਨ ਵਾਲਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਜੋ ਇਸ ਨੂੰ ਆਸਾਨੀ ਨਾਲ ਧੋਇਆ ਜਾ ਸਕੇ । ਪਰ ਰਸੋਈ ਦਾ ਫਰਸ਼ ਤਿਲਕਣਾ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ।
- ਫਰਸ਼ ਦੀ ਤਰ੍ਹਾਂ ਰਸੋਈ ਦੀਆਂ ਦੀਵਾਰਾਂ ਵੀ ਸਾਫ਼ ਹੋ ਸਕਣ ਵਾਲੀਆਂ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਤੇ ਪੇਂਟ ਜਾਂ ਧੋ ਹੋ ਸਕਣ ਵਾਲੇ ਪੇਪਰ ਦਾ ਇਸਤੇਮਾਲ ਵੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
- ਰਸੋਈ ਵਿਚ ਇਕ ਹੀ ਦਰਵਾਜ਼ਾ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿਉਂਕਿ ਜ਼ਿਆਦਾ ਦਰਵਾਜ਼ੇ ਕੰਮ ਕਰਨ ਦੀ ਥਾਂ ਘਟਾਉਂਦੇ ਹਨ ਤੇ ਤੁਰਨ ਫਿਰਨ ਵਿਚ, ਸਮਾਨ ਰੱਖਣ ਵਿਚ ਰੁਕਾਵਟ ਵੀ ਪੈਦਾ ਕਰਦੇ ਹਨ ।
- ਰਸੋਈ ਵਿਚ ਹਵਾ ਤੇ ਰੌਸ਼ਨੀ ਦਾ ਠੀਕ ਪ੍ਰਬੰਧ ਹੋ ਸਕੇ ਇਸ ਲਈ ਇਸ ਨੂੰ ਬਾਹਰ ਵੱਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਧੂਆਂ ਬਾਹਰ ਕੱਢਣ ਲਈ ਚੁਲ੍ਹੇ ਉੱਪਰ ਚਿਮਨੀ (ਜਾਂ ਫਿਰ ਐਗਜ਼ਾਸਟ ਫੈਨ) ਜ਼ਰੂਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਨਹੀਂ ਤਾਂ ਧੂੰਆਂ ਦੂਸਰੇ ਕਮਰਿਆਂ ਵਿਚ ਫੈਲ ਜਾਵੇਗਾ ।
- ਰਸੋਈ ਵਿਚ ਬਿਜਲੀ ਦੇ ਉਪਕਰਨਾਂ ਦੀ ਵਰਤੋਂ ਅਨੁਸਾਰ ਹੀ ਬਿਜਲੀ ਦੇ ਵਿੱਚ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ।
- ਰਸੋਈ ਵਿਚ ਹਮੇਸ਼ਾ ਹਲਕੇ ਰੰਗਾਂ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਹਲਕੇ ਰੰਗ ਖੁੱਲ੍ਹੇਪਨ ਦਾ ਅਹਿਸਾਸ ਕਰਵਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 17.
ਰਸੋਈ ਦੀ ਸਫ਼ਾਈ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਰਸੋਈ ਦੇ ਹਰ ਇਕ ਸਥਾਨ ਨੂੰ ਧੋ-ਪੂੰਝ ਕੇ ਸਾਫ਼ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਭੋਜਨ ਖ਼ਤਮ ਹੋਣ ਤੋਂ ਬਾਅਦ ਬਚਿਆ ਹੋਇਆ ਭੋਜਨ ਦੁਸਰੇ ਸਾਫ਼ ਭਾਂਡਿਆਂ ਵਿਚ ਰੱਖ ਕੇ ਜਾਲੀਦਾਰ ਅਲਮਾਰੀ ਜਾਂ ਰੈਫ਼ਰੀਜਰੇਟਰ ਵਿਚ ਰੱਖ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ । ਜੂਠੇ ਭਾਂਡਿਆਂ ਨੂੰ ਸਾਫ਼ ਕਰਨ ਦੀ ਥਾਂ ਤੇ ਹੀ ਸਾਫ਼ ਕੀਤਾ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ । ਭੋਜਨ ਪਕਾਉਣ ਅਤੇ ਪਰੋਸਣ ਦੇ ਸਥਾਨ ਨੂੰ ਪਹਿਲਾਂ ਗਿੱਲੇ ਅਤੇ ਫਿਰ ਸੁੱਕੇ ਕੱਪੜੇ ਨਾਲ ਪੂੰਝ ਕੇ ਸਾਫ਼ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਭਾਂਡਿਆਂ ਨੂੰ ਸਾਫ਼ ਕਰਕੇ ਉੱਚਿਤ ਸਥਾਨ ਤੇ ਟਿਕਾ ਕੇ ਰੱਖਣਾ ਚਾਹੀਦਾ । ਨਲ, ਫ਼ਰਸ਼, ਸਿੰਕ ਹੁੰਦੀ ਆਦਿ ਨੂੰ ਸਾਫ਼ ਕਰਕੇ ਸੁੱਕਾ ਰੱਖਣ ਦਾ ਯਤਨ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਰਸੋਈ ਘਰ ਦੀ ਚੌਂਕੀ, ਤਖ਼ਤ, ਮੇਜ਼, ਕੁਰਸੀ ਦੀ ਸਫ਼ਾਈ ਵੀ ਹਰ ਰੋਜ਼ ਕੀਤੀ ਜਾਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਫ਼ਰਸ਼ ਨੂੰ ਪਾਣੀ ਨਾਲ ਹਰ ਰੋਜ਼ ਸਾਫ਼ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਸਿੰਕ (ਹਿੰਦੀ) ਨੂੰ ਝਾੜੂ ਨਾਲ ਜਾਂ ਕੂਚੀ ਨਾਲ ਰਗੜ ਕੇ ਧੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਨਿਬੰਧਾਤਮਕ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 18.
ਰਸੋਈ ਸਾਡੇ ਘਰ ਦਾ ਸਭ ਤੋਂ ਜ਼ਰੂਰੀ ਅੰਗ ਹੈ ਕਿਉਂ ?
ਉੱਤਰ-
ਮਨੁੱਖ ਦੀ ਸਾਰੀ ਦੌੜ-ਭੱਜ ਦਾ ਮੁੱਖ ਕਾਰਨ ਅਸਲ ਵਿਚ ਢਿੱਡ ਦੀ ਭੁੱਖ ਨੂੰ ਮਿਟਾਉਣਾ ਹੈ ਤੇ ਦੌੜ ਭੱਜ ਕੀਤੀ ਵੀ ਤਾਂ ਹੀ ਜਾ ਸਕਦੀ ਹੈ ਜੇਕਰ ਢਿੱਡ ਭਰਿਆ ਹੋਵੇ । “ਭੁੱਖੇ ਪੇਟ ਭਜਨ ਨਾ ਹੋਵੇ, ਵਾਲੀ ਕਹਾਵਤ ਤੋਂ ਤਾਂ ਸਾਰੇ ਜਾਣੂ ਹੀ ਹਨ । ਭੋਜਨ ਜਿੱਥੇ ਮਨੁੱਖ ਨੂੰ ਕੰਮ ਕਰਨ ਲਈ ਲੋੜੀਂਦੀ ਊਰਜਾ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ਉੱਥੇ ਉਸ ਨੂੰ ਜੀਵਿਤ ਰੱਖਣ ਵਿਚ ਵੀ ਸਹਾਈ ਹੈ ।
ਪਰ ਭੋਜਨ ਬਣਾਇਆ ਕਿੱਥੇ ਜਾਂਦਾ ਹੈ, ਰਸੋਈ ਵਿਚ । ਇਸ ਤਰ੍ਹਾਂ ਰਸੋਈ ਮਨੁੱਖ ਦੇ ਜੀਵਨ ਵਿਚ ਖ਼ਾਸ ਅਹਿਮੀਅਤ ਰੱਖਦੀ ਹੈ । ਪੁਰਾਣੇ ਸਮਿਆਂ ਤੋਂ ਹੀ ਇਹ ਵੰਡ ਕਰ ਲਈ ਗਈ ਸੀ ਕਿ ਬਾਹਰਲੇ ਕੰਮ ਆਦਮੀ ਕਰੇਗਾ ਅਤੇ ਘਰ ਦੇ ਕੰਮ ਜਿਵੇਂ ਭੋਜਨ ਪਕਾਉਣਾ ਆਦਿ ਹਿਣੀ ਕਰੇਗੀ । ਇਸ ਤਰ੍ਹਾਂ ਜੇ ਆਦਮੀ ਸਾਰਾ ਦਿਨ ਘਰੋਂ ਬਾਹਰ ਕੰਮ ਕਰਦਾ ਹੈ ਤਾਂ ਹਿਣੀ ਵੀ ਲਗਪਗ ਸਾਰਾ ਦਿਨ ਸੁਆਦਲੇ ਅਤੇ ਸਿਹਤਮੰਦ ਭੋਜਨ ਦੀ ਤਿਆਰੀ ਵਿਚ ਰਸੋਈ ਵਿਚ ਹੀ ਬਿਤਾਉਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਰਸੋਈ ਸਾਡੇ ਘਰ ਅਤੇ ਜ਼ਿੰਦਗੀ ਦਾ ਜ਼ਰੂਰੀ ਅੰਗ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 19.
ਰਸੋਈ ਬਣਾਉਣ ਸਮੇਂ ਤੁਸੀਂ ਕਿਨ੍ਹਾਂ-ਕਿਨ੍ਹਾਂ ਗੱਲਾਂ ਨੂੰ ਧਿਆਨ ਵਿਚ ਰੱਖੋਗੇ ?
ਉੱਤਰ-
ਰਸੋਈ ਦੀ ਯੋਜਨਾ ਬਣਾਉਣ ਵੇਲੇ ਵਿਚਾਰਨ ਵਾਲੀਆਂ ਗੱਲਾਂ ਇਸ ਤਰ੍ਹਾਂ ਹਨ-
- ਪਾਣੀ ਲਈ ਹਿੰਦੀ ਵਿਚ ਟੁਟੀ ਦਾ ਪ੍ਰਬੰਧ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਜਾਂ ਫਿਰ ਕਿਸੇ ਬਾਲਟੀ ਆਦਿ ਨੂੰ ਟੂਟੀ ਲਾ ਕੇ ਪਾਣੀ ਨਾਲ ਭਰ ਕੇ ਰੱਖ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਰਸੋਈ ਵਿਚ ਸਮਾਨ ਰੱਖਣ ਲਈ ਅਲਮਾਰੀਆਂ, ਰੈਕ ਆਦਿ ਤੇ ਕੜਛੀਆਂ, ਚਮਚੇ, ਚਾਕੂ ਆਦਿ ਟੰਗਣ ਲਈ ਖੁੰਟੀਆਂ ਆਦਿ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ।
- ਰਸੋਈ ਦਾ ਫਰਸ਼ ਪੱਕਾ ਸੰਗਮਰਮਰ, ਰੰਗਦਾਰ ਟਾਇਲਾ, ਲਿਨੋਲੀਅਮ ਆਦਿ ਦਾ ਅਤੇ ਜਲਦੀ ਸਾਫ਼ ਹੋ ਸਕਣ ਵਾਲਾ ਅਤੇ ਜ਼ਿਆਦਾ ਢਲਾਨ ਵਾਲਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਜੋ ਇਸ ਨੂੰ ਆਸਾਨੀ ਨਾਲ ਧੋਇਆ ਜਾ ਸਕੇ । ਪਰ ਰਸੋਈ ਦਾ ਫਰਸ਼ ਤਿਲਕਣਾ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ।
- ਫਰਸ਼ ਦੀ ਤਰ੍ਹਾਂ ਰਸੋਈ ਦੀਆਂ ਦੀਵਾਰਾਂ ਵੀ ਸਾਫ਼ ਹੋ ਸਕਣ ਵਾਲੀਆਂ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਤੇ ਪੇਂਟ ਜਾਂ ਧੋ ਹੋ ਸਕਣ ਵਾਲੇ ਪੇਪਰ ਦਾ ਇਸਤੇਮਾਲ ਵੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
- ਰਸੋਈ ਵਿਚ ਇਕ ਹੀ ਦਰਵਾਜ਼ਾ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿਉਂਕਿ ਜ਼ਿਆਦਾ ਦਰਵਾਜ਼ੇ ਕੰਮ ਕਰਨ ਦੀ ਥਾਂ ਘਟਾਉਂਦੇ ਹਨ ਤੇ ਤੁਰਨ ਫਿਰਨ ਵਿਚ, ਸਮਾਨ ਰੱਖਣ ਵਿਚ ਰੁਕਾਵਟ ਵੀ ਪੈਦਾ ਕਰਦੇ ਹਨ ।
- ਰਸੋਈ ਵਿਚ ਹਵਾ ਤੇ ਰੌਸ਼ਨੀ ਦਾ ਠੀਕ ਪ੍ਰਬੰਧ ਹੋ ਸਕੇ ਇਸ ਲਈ ਇਸ ਨੂੰ ਬਾਹਰ ਵੱਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਧੂਆਂ ਬਾਹਰ ਕੱਢਣ ਲਈ ਚੁਲ੍ਹੇ ਉੱਪਰ ਚਿਮਨੀ (ਜਾਂ ਫਿਰ ਐਗਜ਼ਾਸਟ ਫੈਨ) ਜ਼ਰੂਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਨਹੀਂ ਤਾਂ ਧੂੰਆਂ ਦੂਸਰੇ ਕਮਰਿਆਂ ਵਿਚ ਫੈਲ ਜਾਵੇਗਾ ।
- ਰਸੋਈ ਵਿਚ ਬਿਜਲੀ ਦੇ ਉਪਕਰਨਾਂ ਦੀ ਵਰਤੋਂ ਅਨੁਸਾਰ ਹੀ ਬਿਜਲੀ ਦੇ ਵਿੱਚ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ।
- ਰਸੋਈ ਵਿਚ ਹਮੇਸ਼ਾ ਹਲਕੇ ਰੰਗਾਂ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਹਲਕੇ ਰੰਗ ਖੁੱਲ੍ਹੇਪਨ ਦਾ ਅਹਿਸਾਸ ਕਰਵਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 20.
ਨਵੇਂ ਅਤੇ ਪੁਰਾਣੀ ਕਿਸਮ ਦੀਆਂ ਰਸੋਈਆਂ ਬਾਰੇ ਦੱਸੋ ਅਤੇ ਇਹਨਾਂ ਵਿਚ ਕੀ ਅੰਤਰ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਰਸੋਈ ਦੀਆਂ ਕਿਸਮਾਂ-
1. ਪੁਰਾਣੀ ਕਿਸਮ-ਪੁਰਾਣੀ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਆਮ ਤੌਰ ‘ਤੇ ਸਾਰਾ ਕੰਮ ਜ਼ਮੀਨ ਤੇ ਬੈਠ ਕੇ ਹੀ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਬਹੁਤੇ ਘਰਾਂ ਖ਼ਾਸ ਕਰਕੇ ਪਿੰਡਾਂ ਵਿਚ ਇਸ ਤਰ੍ਹਾਂ ਦੀਆਂ ਹੀ ਰਸੋਈਆਂ ਹਨ | ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਅੰਗੀਠੀ ਜਾਂ ਚੁੱਲਾ ਜ਼ਮੀਨ ਤੇ ਹੀ ਬਣਾਇਆ ਹੁੰਦਾ ਹੈ । ਬੈਠਣ ਲਈ ਪਟੜੇ ਜਾਂ ਪੀੜ੍ਹੀ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਰਸੋਈ ਵਿਚ ਹੀ ਪੀੜ੍ਹੀ ਜਾਂ ਪਟੜੇ ਤੇ ਬੈਠ ਕੇ ਖਾਣਾ ਖਾ ਲਿਆ ਜਾਂਦਾ ਹੈ ।
ਬੈਠ ਕੇ ਖਾਣਾ ਪਕਾਉਂਦੇ ਸਮੇਂ ਕੋਈ ਵੀ ਚੀਜ਼ ਲੈਣ ਜਾਂ ਰੱਖਣ ਵੇਲੇ ਬਾਰ-ਬਾਰ ਉੱਠਣਾ ਪੈਂਦਾ ਹੈ ਜਿਵੇਂ ਬਰਤਨ, ਭੋਜਨ, ਪਾਣੀ ਜਾਂ ਕੋਈ ਹੋਰ ਚੀਜ਼ । ਇਸ ਤਰ੍ਹਾਂ ਉੱਠਣ-ਬੈਠਣ ਤੇ ਕਾਫ਼ੀ ਸਮਾਂ ਅਤੇ ਸ਼ਕਤੀ ਲੱਗ ਜਾਂਦੀ ਹੈ ਕਿਉਂਕਿ ਸਾਰਾ ਸਮਾਨ ਬੈਠਣ ਵਾਲੀ ਜਗਾ ਦੇ ਨੇੜੇ ਨਹੀਂ ਰੱਖਿਆ ਜਾ ਸਕਦਾ | ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਸ਼ਕਤੀ ਵੱਧ ਲੱਗਣ ਕਾਰਨ ਸਰੀਰ ਨੂੰ ਵੱਧ ਤਕਲੀਫ਼ ਰਸੋਈ ਦਾ ਪ੍ਰਬੰਧ ਦੇਣੀ ਪੈਂਦੀ ਹੈ । ਸਫ਼ਾਈ ਦੇ ਪੱਖ ਤੋਂ ਵੀ ਇਸ ਤਰੀਕੇ ਨੂੰ ਸਹੀ ਨਹੀਂ ਕਿਹਾ ਜਾ ਸਕਦਾ ਕਿਉਂਕਿ ਕੰਮ ਕਰਦੇ ਹੋਏ ਸਾਰਾ ਸਮਾਨ ਜ਼ਮੀਨ ਤੇ ਹੀ ਰੱਖਣਾ ਪੈਂਦਾ ਹੈ ।
2. ਨਵੀਂ ਕਿਸਮ ਦੀਆਂ ਰਸੋਈਆਂ – ਵਿਗਿਆਨ ਨੇ ਤਰੱਕੀ ਨਾਲ ਨਵੇਂ-ਨਵੇਂ ਉਪਕਰਨਾਂ ਦੀ ਕਾਢ ਹੋਈ ਅਤੇ ਇਹਨਾਂ ਦੀ ਵਰਤੋਂ ਨਾਲ ਕੰਮ ਸੌਖੇ ਤਰੀਕੇ ਨਾਲ ਅਤੇ ਘੱਟ ਸਮੇਂ ਵਿਚ ਹੋਣ ਲੱਗ ਪਿਆ ਹੈ । ਸਮੇਂ ਅਤੇ ਸ਼ਕਤੀ ਦੀ ਬੱਚਤ ਹੋ ਸਕੇ ਇਸ ਲਈ ਨਵੇਂ ਕਿਸਮ ਦੀਆਂ ਰਸੋਈਆਂ ਬਣਨ ਲੱਗ ਗਈਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਖੜੇ ਖੜੇ ਹੀ ਸਾਰੇ ਕੰਮ ਕਰ ਲਏ ਜਾਂਦੇ ਹਨ । ਬਾਰ-ਬਾਰ ਉੱਠਣ ਬੈਠਣ ਲਈ ਸਮਾਂ ਅਤੇ ਸ਼ਕਤੀ ਵਿਅਰਥ ਨਹੀਂ ਜਾਂਦੇ । ਫਰਿਜ਼ ਲਈ ਆਮ ਕਰਕੇ ਰਸੋਈ ਵਿਚ ਹੀ ਥਾਂ ਬਣਾ ਲਈ ਜਾਂਦੀ ਹੈ । ਕੰਮ ਕਰਨ ਲਈ ਜੋ ਸ਼ੈਲਫ਼ ਹੁੰਦੀ ਉਸ ਅਨੁਸਾਰ ਪੰਜ ਕਿਸਮ ਦੀਆਂ ਰਸੋਈਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ-
- ਇਕ ਦੀਵਾਰ ਵਾਲੀ .
- ਦੋ ਦੀਵਾਰਾਂ ਵਾਲੀ
- ਐੱਲ (L) ਸ਼ਕਲ ਵਾਲੀ
- ਯੂ. (U) ਸ਼ੇਕਲੇ ਵਾਲੀ
- ਟੁੱਟਿਆ ਯੂ. (U) ਸ਼ਕਲ ਵਾਲੀ ।
ਨਵੀਂ ਕਿਸਮ ਅਤੇ ਪੁਰਾਣੀ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਅੰਤਰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-
| ਨਵੀਂ ਕਿਸਮ | ਪੁਰਾਣੀ ਕਿਸਮ |
| (1) ਇਸ ਵਿਚ ਸਾਰੇ ਕੰਮ ਖੜ੍ਹੇ ਹੋ ਕੇ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । | (1) ਇਸ ਵਿਚ ਸਾਰੇ ਕੰਮ ਬੈਠ ਕੇ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । |
| (2) ਗੈਸ, ਚੁੱਲ੍ਹੇ ਜਾਂ ਨਵੇਂ ਉਪਕਰਨਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । | (2) ਉਹੀ ਪੁਰਾਣੇ ਚੁੱਲਿਆਂ, ਸਟੋਵਾਂ ਜਾਂ ਅੰਗੀਠੀਆਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । |
| (3) ਸਮਾਂ ਅਤੇ ਸ਼ਕਤੀ ਦੀ ਬੱਚਤ ਹੋ ਜਾਂਦੀ ਹੈ । | (3) ਸਮਾਂ ਅਤੇ ਸ਼ਕਤੀ ਦੋਵੇਂ ਵਿਅਰਥ ਹੁੰਦੇ ਹਨ । |
| (4) ਭੋਜਨ ਪਕਾਉਣ ਵੇਲੇ ਸਫ਼ਾਈ ਦਾ ਧਿਆਨ ਰੱਖਿਆ ਜਾ ਸਕਦਾ ਹੈ । | (4) ਕਿਉਂਕਿ ਸਾਰਾ ਸਮਾਨ ਜ਼ਮੀਨ ਤੇ ਰੱਖਣਾ ਪੈਂਦਾ ਹੈ ਇਸ ਲਈ ਸਫ਼ਾਈ ਦੇ ਪੱਖ ਤੋਂ ਇਹ ਰਸੋਈ ਵਧੀਆ ਨਹੀਂ ਹੈ । |
ਪ੍ਰਸ਼ਨ 21.
ਰਸੋਈ ਦੀ ਸਫ਼ਾਈ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ? ਇਸ ਦੇ ਅੰਤਰਗਤ ਕੀ-ਕੀ ਆਉਂਦਾ
ਉੱਤਰ-
ਰਸੋਈ ਦੀ ਸਫ਼ਾਈ ਬਹੁਤ ਹੀ ਜ਼ਰੂਰੀ ਹੈ ਕਿਉਂਕਿ ਰਸੋਈ ਵਿਚ ਖਾਧ ਪਦਾਰਥ ਰੱਖੇ ਜਾਂਦੇ ਹੁੰਦੇ ਹਨ ਇਸ ਲਈ ਜੇਕਰ ਸਫ਼ਾਈ ਨਾ ਰੱਖੀ ਜਾਵੇ ਤਾਂ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਜੀਵ ਜੰਤੂ ਪੈਦਾ ਹੋ ਜਾਂਦੇ ਹਨ ।
ਖਾਧ ਪਦਾਰਥਾਂ ਵਾਲੀਆਂ ਅਲਮਾਰੀਆਂ ਵਿਚ ਜ਼ਹਿਰੀਲੇ ਰਸਾਇਣ ਪਦਾਰਥ ਜਾਂ ਕੀੜੇ ਮਾਰ ਦਵਾਈਆਂ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕੀਤੀ ਜਾ ਸਕਦੀ । ਜੀਵ ਜੰਤੂ ਪੈਦਾ ਹੀ ਨਾ ਹੋਣ ਇਸ ਲਈ ਰਸੋਈ ਦੀ ਸਫ਼ਾਈ ਕਰਦੇ ਰਹਿਣਾ ਲਾਜ਼ਮੀ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਰਸੋਈ ਦੀ ਸਫ਼ਾਈ ਆਸਾਨੀ ਨਾਲ ਕੀਤੀ ਜਾ ਸਕੇ ਇਸ ਲਈ ਫਰਸ਼ ਪੱਕੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
ਖਾਣਾ ਪਕਾਉਣ ਤੋਂ ਬਾਅਦ ਰਸੋਈ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਧੋਵੋ ਅਤੇ ਹਫ਼ਤੇ ਵਿਚ ਇਕ ਵਾਰ ਸਾਬਣ, ਡਿਟਰਜੈਂਟ ਜਾਂ ਸੋਡੇ ਵਾਲੇ ਗਰਮ ਪਾਣੀ ਨਾਲ ਰਸੋਈ ਨੂੰ ਜ਼ਰੂਰ ਸਾਫ਼ ਕਰੋ । ਚੁੱਲ੍ਹੇ ਦੀ ਸਫ਼ਾਈ ਹਰ ਰੋਜ਼ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਰਸੋਈ ਧੋਣ ਤੋਂ ਬਾਅਦ ਪੋਚਾ ਫੇਰ ਕੇ ਸੁਕਾ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ ।
ਰਸੋਈ ਦੀਆਂ ਅਲਮਾਰੀਆਂ, ਡੱਬੇ ਰੱਖਣ ਵਾਲੀਆਂ ਥਾਵਾਂ, ਦੀਵਾਰਾਂ ਅਤੇ ਛੱਤਾਂ ਨੂੰ ਵੀ ਹਫ਼ਤੇ ਜਾਂ ਪੰਦਰਾਂ ਦਿਨਾਂ ਵਿਚ ਇਕ ਵਾਰ ਜ਼ਰੂਰ ਸਾਫ਼ ਕਰ ਲਓ । ਰਸੋਈ ਵਿਚ ਬੇਲੋੜਾ ਸਮਾਨ ਇੱਕਠਾ ਨਾ ਕਰੋ, ਵੱਡੇ ਬਰਤਨ ਜਾਂ ਫਾਲਤੂ ਡੱਬਿਆਂ ਨੂੰ ਇੱਕਠਾ ਕਰਕੇ ਸਟੋਰ ਵਿਚ ਰੱਖ ਦਿਓ । ਕਦੇ-ਕਦੇ ਇਹਨਾਂ ਬਰਤਨਾਂ ਅਤੇ ਸਟੋਰ ਦੀ ਵੀ ਸਫ਼ਾਈ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
ਰਸੋਈ ਦੀਆਂ ਦੀਵਾਰਾਂ ਵਿਚ ਸਲ੍ਹਾਬ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ ।ਜੇ ਉੱਲੀ ਆਦਿ ਲੱਗ ਜਾਵੇ ਤਾਂ ਦਵਾਈ ਆਦਿ ਨਾਲ ਇਸ ਨੂੰ ਦੂਰ ਕਰੋ । | ਰਸੋਈ ਵਿਚ ਢੱਕਣ ਵਾਲੇ ਕੂੜੇਦਾਨ ਦੀ ਵਰਤੋਂ ਕਰੋ ( ਕੂੜਾ ਇਸ ਵਿਚ ਹੀ ਪਾਓ ਪਰ ਇਕੱਠਾ ਨਾ ਹੋਣ ਦਿਓ ਨਹੀਂ ਤਾਂ ਮੱਖੀ, ਮੱਛਰ ਪੈਦਾ ਹੋਣ ਲੱਗ ਜਾਂਦੇ ਹਨ ।
ਰਸੋਈ ਅੰਦਰ ਅਲੱਗ ਜੁੱਤੀਆਂ ਦੀ ਵਰਤੋਂ ਕਰੋ । ਕਿਉਂਕਿ ਬਾਹਰ ਪਹਿਣਨ ਵਾਲੀਆਂ ਜੁੱਤੀਆਂ ‘ਤੇ ਗੰਦ-ਮੰਦ ਲੱਗਾ ਹੋ ਸਕਦਾ ਹੈ । ਰਸੋਈ ਅੱਗੇ ਪਾਏਦਾਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਜੋ ਹਰ ਕੋਈ ਪੈਰ ਪੂੰਝ ਕੇ ਹੀ ਅੰਦਰ ਵੜੇ ।
![]()
PSEB 9th Class Home Science Guide ਰਸੋਈ ਦਾ ਪ੍ਰਬੰਧ Important Questions and Answers
ਕੁੱਝ ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਪ੍ਰਸ਼ਨ
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਪਹਿਲਾਂ ਚੁੱਲ੍ਹੇ ਇਕ ਪਾਸੇ ਵਿਹੜੇ ਵਿਚ ਕਿਉਂ ਬਣਾਏ ਜਾਂਦੇ ਸਨ ?
ਉੱਤਰ-
ਕਿਉਂਕਿ ਪਹਿਲਾਂ ਧੂੰਏਂ ਵਾਲਾ ਬਾਲਣ ਵਰਤਿਆ ਜਾਂਦਾ ਸੀ ਇਸ ਲਈ ਕਮਰਿਆਂ ਦੇ ਅੰਦਰ ਰਸੋਈ ਦਾ ਚੁੱਲ੍ਹਾ ਨਹੀਂ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਸੀ । ਇਸ ਲਈ ਚੁੱਲਾ ਇਕ ਪਾਸੇ ਵਿਹੜੇ ਵਿਚ ਹੀ ਬਣਾਇਆ ਜਾਂਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 2.
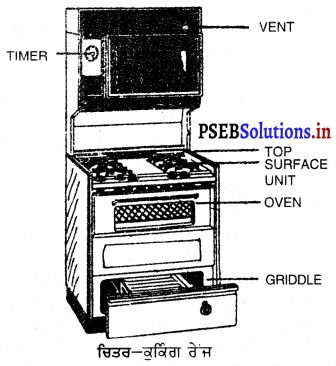
ਅੱਜ-ਕੱਲ੍ਹ ਰਸੋਈ ਵਿਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਬਾਲਣਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਦਾ ਤੇਲ, ਗੋਬਰ ਗੈਸ, ਖਾਣਾ ਪਕਾਉਣ ਵਾਲੀ ਗੈਸ ਅਤੇ ਬਿਜਲੀ ਆਦਿ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਖ਼ਾਸ ਪਕਵਾਨ ਬਣਾਉਣ ਸਮੇਂ ਯੋਜਨਾ ਕਿਉਂ ਬਣਾਉਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਖ਼ਾਸ ਪਕਵਾਨ ਬਣਾਉਣ ਲਈ ਕਈ ਖ਼ਾਸ ਵਸਤਾਂ, ਖਾਧ ਪਦਾਰਥਾਂ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਪਹਿਲਾਂ ਜ਼ਰੂਰੀ ਵਸਤਾਂ ਦੀ ਸੂਚੀ ਤੇ ਪਕਾਉਣ ਦੀ ਯੋਜਨਾ ਬਣਾ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ । ਮੰਨ ਲਉ ਬਿਨਾਂ ਯੋਜਨਾ ਤੋਂ ਕੇਸਰ ਕੁਲਫ਼ੀ ਬਣਾਉਣ ਲੱਗ ਜਾਈਏ ਤੇ ਬਾਅਦ ਵਿਚ ਘਰ ਵਿਚ ਕੇਸਰ ਹੀ ਨਾ ਹੋਵੇ ਤੇ ਮਾਯੂਸੀ ਦਾ ਸਾਮਣਾ ਕਰਨਾ ਪਵੇਗਾ ।
ਪ੍ਰਸ਼ਨ 4.
ਰਸੋਈ ਵਿਚ ਸ਼ੈਲਫਾਂ ਦੀ ਉਚਾਈ ਕਿੰਨੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਰਸੋਈ ਵਿਚ ਆਮ ਤੌਰ ਤੇ ਸੈਲਫਾਂ ਦੀ ਉਚਾਈ ਢਾਈ ਫੁੱਟ ਹੁੰਦੀ ਹੈ, ਪਰ ਹਿਣੀ ਦੀ ਲੰਬਾਈ ਅਨੁਸਾਰ ਵੱਧ ਜਾਂ ਘੱਟ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਪੁਰਾਣੇ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਸਮਾਂ ਤੇ ਸ਼ਕਤੀ ਕਿਵੇਂ ਨਸ਼ਟ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਵਾਰ-ਵਾਰ ਉੱਠਣ-ਬੈਠਣ ਨਾਲ ਸਮਾਂ ਤੇ ਸ਼ਕਤੀ ਨਸ਼ਟ ਹੁੰਦੇ ਹਨ ਕਿਉਂਕਿ ਸਾਰਾ ਸਮਾਨ ਜ਼ਮੀਨ ਤੇ ਨਹੀਂ ਰੱਖਿਆ ਜਾ ਸਕਦਾ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਰਸੋਈ ਵਿਚ ਕੰਮ ਕਰਨ ਦੇ ਕੇਂਦਰਾਂ ਦੀ ਯੋਜਨਾ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਹੋਣੀ ਚਾਹੀਦੀ
ਹੈ ?
ਉੱਤਰ-
ਇਸ ਲਈ ਯੋਜਨਾ ਇਸ ਤਰ੍ਹਾਂ ਬਣਾਓ ਕਿ ਕੰਮ ਵਾਲੇ ਨੂੰ ਵੱਧ ਤੋਂ ਵੱਧ ਥਾਂ ਉਪਲੱਬਧ ਹੋਵੇ ਅਤੇ ਘੱਟ ਤੋਂ ਘੱਟ ਚਲਣਾ ਪਵੇ । ਕੰਮ ਕਰਨ ਦੇ ਤਿੰਨਾਂ ਕੇਂਦਰਾਂ ਵਿਚ ਤਾਲਮੇਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਰਸੋਈ ਵਿਚ ਵੱਧ ਦਰਵਾਜ਼ੇ ਕਿਉਂ ਨਹੀਂ ਹੋਣੇ ਚਾਹੀਦੇ ?
ਉੱਤਰ-
ਵੱਧ ਦਰਵਾਜ਼ੇ ਇਕ ਤਾਂ ਥਾਂ ਵੱਧ ਘੇਰਨਗੇ ਤੇ ਇਕ ਕੰਮ ਵਿਚ ਰੁਕਾਵਟ ਪਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 8.
ਰਸੋਈ ਵਿਚ ਉੱਲੀ ਦਾ ਕੰਟਰੋਲ ਕਿਵੇਂ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਰਸੋਈ ਵਿਚ ਉੱਲੀ ਦਾ ਕੰਟਰੋਲ ਕਰਨ ਲਈ ਨੀਲਾ ਥੋਥਾ ਦੋ ਹਿੱਸੇ ਜਾਂ ਬੋਰਿਕ ਪਾਊਡਰ ਇਕ ਹਿੱਸਾ ਨੂੰ 20 ਹਿੱਸੇ ਪਾਣੀ ਵਿਚ ਘੋਲ ਕੇ ਉੱਲੀ ਵਾਲੀ ਥਾਂ ਧੋ ਦੇਣੀ ਚਾਹੀਦੀ ਹੈ ।
ਵੱਡੇ ਉੱਤਰ ਵਾਲਾ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਇਕ ਦੀਵਾਰ ਵਾਲੀ ਅਤੇ ਦੋ ਦੀਵਾਰਾਂ ਵਾਲੀ ਰਸੋਈ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
1. ਇਕ ਵਾਰ ਵਾਲੀ ਰਸੋਈ-ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਭੋਜਨ ਦੀ ਤਿਆਰੀ, ਖਾਣਾ ਪਕਾਉਣਾ ਅਤੇ ਵਰਤਾਉਣ ਦਾ ਕੇਂਦਰ ਅਤੇ ਰੌਦੀ ਸਭ ਕੁਝ ਇਕ ਹੀ ਦੀਵਾਰ ਦੇ ਨਾਲ ਹੁੰਦਾ ਹੈ ਇਸ ਲਈ ਇਸ ਵਿਚ ਵਧੇਰੇ ਤੁਰਨਾ ਫਿਰਨਾ ਪੈਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਂ ਤੇ ਸ਼ਕਤੀ ਵੱਧ ਲਗਦੇ ਹਨ ।
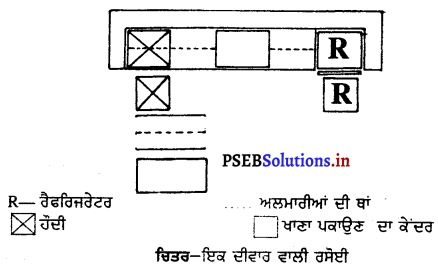
2. ਦੋ ਦੀਵਾਰਾਂ ਵਾਲੀ-ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਆਮਣੇ-ਸਾਹਮਣੇ ਦੋਵਾਂ ਦੀਵਾਰਾਂ ਤੇ ਸ਼ੈਲਫ਼ਾਂ ਬਣੀਆਂ ਹੁੰਦੀਆਂ ਹਨ। ਕੰਮ ਕਰਨ ਦੇ ਦੋ ਕੇਂਦਰ ਇਕ ਦੀਵਾਰ ਨਾਲ ਅਤੇ ਤੀਸਰਾ ਕੇਂਦਰ ਸਾਹਮਣੇ ਵਾਲੀ ਦੀਵਾਰ ਨਾਲ ਹੁੰਦੇ ਹਨ | ਅਜਿਹੀ ਰਸੋਈ ਵਿਚ ਕਾਫ਼ੀ ਥਾਂ ਹੁੰਦੀ ਹੈ ਤੇ ਜਗਾ ਦੀ ਮੁਸ਼ਕਿਲ ਨਹੀਂ ਹੁੰਦੀ ਪਰ ਜੇ ਦੋਨੋਂ ਪਾਸੇ ਦਰਵਾਜ਼ੇ ਹੋਣ ਤਾਂ ਰਸੋਈ ਲਾਂਘਾ ਹੀ ਬਣ ਜਾਂਦੀ ਹੈ ।
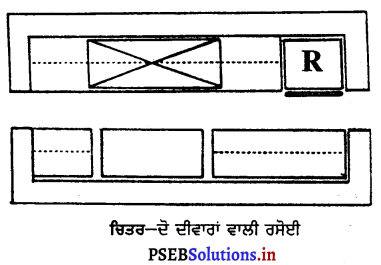
![]()
ਵਸਤੁਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ
ਖ਼ਾਲੀ ਥਾਂ ਭਰੋ
1. ਪੁਰਾਣੀ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਸਾਰੇ ਕੰਮ …………………… ਕੇ ਕੀਤੇ ਜਾਂਦੇ ਸਨ ।
2. ਰਸੋਈ ਵਿਚ ਕੰਮ ਕਰਨ ਲਈ …………………… ਕੇਂਦਰ ਹੁੰਦੇ ਹਨ ।
3. ਸਾਧਾਰਨ ਪਰਿਵਾਰ ਲਈ ਰਸੋਈ ਦਾ ਆਕਾਰ ……………………… ਹੁੰਦਾ ਹੈ ।
4. ਨਵੀਂ ਕਿਸਮ ਦੀਆਂ ਰਸੋਈਆਂ ……………………. ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ।
5. ਰਸੋਈ ਵਿਚ ਉੱਲੀ ਤੋਂ ਬਚਾਓ ਲਈ ਨੀਲੇ ਥੋਥੇ ਅਤੇ …………………….. ਦੇ ਘੋਲ ਦੀ ਵਰਤੋਂ ਕਰੋ ।
ਉੱਤਰ-
1. ਬੈਠ,
2. ਤਿੰਨ,
3. 9×10 ਫੁੱਟ,
4. ਪੰਜ,
5. ਬੋਰਿਕ ਪਾਊਡਰ ।
ਇਕ ਸ਼ਬਦ ਵਿਚ ਉੱਤਰ ਦਿਓ
ਪ੍ਰਸ਼ਨ 1.
ਰਸੋਈ ਵਿਚ ਸ਼ੈਲਫ਼ਾਂ ਦੀ ਸਾਧਾਰਨ ਉਚਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਢਾਈ ਫੁੱਟ ਨੂੰ
ਪ੍ਰਸ਼ਨ 2.
ਰਸੋਈ ਦਾ ਫ਼ਰਸ਼ ਨਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਪੱਕਾ ।
ਪ੍ਰਸ਼ਨ 3.
ਰਸੋਈ ਵਿਚ ਕਿੰਨੇ ਦਰਵਾਜ਼ੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਕ ਹੀ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਰਸੋਈ ਵਿਚ ਕਿਹੋ ਜਿਹੇ ਰੰਗ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਹਲਕੇ ਰੰਗ ਦੀ ।
ਪ੍ਰਸ਼ਨ 5.
ਰਸੋਈ ਵਿਚ ਕਿਹੋ ਜਿਹੇ ਕੂੜੇਦਾਨ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਢੱਕਣ ਵਾਲੇ ।
ਠੀਕ/ਗਲਤ ਦੱਸੋ
1. ਰਸੋਈ ਦੇ ਕੰਮ ਨੂੰ ਤਿੰਨ ਕਾਰਜ ਖੇਤਰਾਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
2. ਰਸੋਈ ਵਿੱਚ ਹਲਕੇ ਰੰਗਾਂ ਦਾ ਇਸਤੇਮਾਲ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
3. ਰਸੋਈ ਦੇ ਦਰਵਾਜ਼ੇ ਖੁੱਲ੍ਹੇ ਰੱਖਣੇ ਚਾਹੀਦੇ ਹਨ ।
ਉੱਤਰ-
ਗ਼ਲਤ
4. ਆਮ ਘਰਾਂ ਵਿੱਚ L ਆਕਾਰ ਦੀ ਰਸੋਈ ਪ੍ਰਚਲਿਤ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
5. ਰਸੋਈ ਦੀਆਂ ਸ਼ੈਲਫ਼ਾਂ ਦੀ ਉਚਾਈ ਢਾਈ ਫੁੱਟ ਹੁੰਦੀ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
![]()
6. ਰਸੋਈ ਦਾ ਫ਼ਰਸ਼ ਪੱਕਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
ਬਹੁ-ਵਿਕਲਪੀ
ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚ ਠੀਕ ਹੈ-
(A) ਪੁਰਾਣੀ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿਚ ਸਾਰਾ ਕੰਮ ਜ਼ਮੀਨ ਤੇ ਬੈਠ ਕੇ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ।
(B) ਨਵੀਂ ਕਿਸਮ ਦੀ ਰਸੋਈ ਵਿੱਚ ਸਮਾਂ ਤੇ ਸ਼ਕਤੀ ਦੀ ਬੱਚਤ ਹੋ ਜਾਂਦੀ ਹੈ
(C) ਰਸੋਈ ਦੀਆਂ ਦੀਵਾਰਾਂ ਤੇ ਸਲ੍ਹਾਬ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ
(D) ਸਾਰੇ ਠੀਕ ।
ਉੱਤਰ-
(D) ਸਾਰੇ ਠੀਕ ।
ਪ੍ਰਸ਼ਨ 2.
ਗਲਤ ਤੱਥ ਹੈ-
(A) ਰਸੋਈ ਅਜਿਹੀ ਥਾਂ ਤੇ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਜਿੱਥੇ ਹਵਾ ਅਤੇ ਸਿੱਧੀ ਰੋਸ਼ਨੀ ਪਹੁੰਚ ਸਕੇ .
(B) ਰਸੋਈ ਦੇ ਦਰਵਾਜ਼ੇ ਅਤੇ ਖਿੜਕੀਆਂ ਤੇ ਜਾਲੀ ਲੱਗੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਦਰਵਾਜ਼ੇ ਹਮੇਸ਼ਾ ਖੁੱਲ੍ਹੇ ਰੱਖਣੇ ਚਾਹੀਦੇ ਹਨ
(C) ਗ੍ਰਹਿਣੀ ਰਸੋਈ ਦੀ ਮਾਲਕਣ ਹੁੰਦੀ ਹੈ, ਉਸ ਦਾ ਕਾਫ਼ੀ ਸਮਾਂ ਰਸੋਈ ਵਿਚ ਬਤੀਤ ਹੁੰਦਾ ਹੈ
(D) ਸਾਰੇ ਗ਼ਲਤ ਹਨ ।
ਉੱਤਰ-
(B) ਰਸੋਈ ਦੇ ਦਰਵਾਜ਼ੇ ਅਤੇ ਖਿੜਕੀਆਂ ਤੇ ਜਾਲੀ ਲੱਗੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਦਰਵਾਜ਼ੇ ਹਮੇਸ਼ਾ ਖੁੱਲ੍ਹੇ ਰੱਖਣੇ ਚਾਹੀਦੇ ਹਨ