Bhagya

zxPunjab State Board Syllabus PSEB 11th Class Maths Book Solutions Guide Pdf in English Medium and Punjabi Medium are part of PSEB Solutions for Class 11.

PSEB 11th Class Maths Guide | Maths Guide for Class 11 PSEB in English Medium

PSEB 11 Class Math Book Pdf Chapter 1 Sets

• Chapter 1 Sets Ex 1.1
• Chapter 1 Sets Ex 1.2
• Chapter 1 Sets Ex 1.3
• Chapter 1 Sets Ex 1.4
• Chapter 1 Sets Ex 1.5
• Chapter 1 Sets Ex 1.6
• Chapter 1 Sets Miscellaneous Exercise

Punjab Board Maths Book Class 11 Solutions Chapter 2 Relations and Function

• Chapter 2 Relations and Functions Ex 2.1
• Chapter 2 Relations and Functions Ex 2.2
• Chapter 2 Relations and Functions Ex 2.3
• Chapter 2 Relations and Functions Miscellaneous Exercise

11th Class Math Book PSEB Chapter 3 Trigonometric Functions

• Chapter 3 Trigonometric Functions Ex 3.1
• Chapter 3 Trigonometric Functions Ex 3.2
• Chapter 3 Trigonometric Functions Ex 3.3
• Chapter 3 Trigonometric Functions Ex 3.4
• Chapter 3 Trigonometric Functions Miscellaneous Exercise

PSEB Class 11 Maths Solutions Chapter 4 Principle of Mathematical Induction

• Chapter 4 Principle of Mathematical Induction Ex 4.1

PSEB Class 11 Maths Book Pdf Download Chapter 5 Complex Numbers and Quadratic Equations

• Chapter 5 Complex Numbers and Quadratic Equations Ex 5.1
• Chapter 5 Complex Numbers and Quadratic Equations Ex 5.2
• Chapter 5 Complex Numbers and Quadratic Equations Ex 5.3
• Chapter 5 Complex Numbers and Quadratic Equations Miscellaneous Exercise

PSEB Class 11 Maths Syllabus Chapter 6 Linear Inequalities

• Chapter 6 Linear Inequalities Ex 6.1
• Chapter 6 Linear Inequalities Ex 6.2
• Chapter 6 Linear Inequalities Ex 6.3
• Chapter 6 Linear Inequalities Miscellaneous Exercise

PSEB 11th Class Math Book Pdf Chapter 7 Permutations and Combinations

• Chapter 7 Permutations and Combinations Ex 7.1
• Chapter 7 Permutations and Combinations Ex 7.2
• Chapter 7 Permutations and Combinations Ex 7.3
• Chapter 7 Permutations and Combinations Ex 7.4
• Chapter 7 Permutations and Combinations Miscellaneous Exercise

11th Class Maths Solutions PSEB Chapter 8 Binomial Theorem

• Chapter 8 Binomial Theorem Ex 8.1
• Chapter 8 Binomial Theorem Ex 8.2
• Chapter 8 Binomial Theorem Miscellaneous Exercise

PSEB 11th Class Maths Solutions Chapter 9 Sequences and Series

• Chapter 9 Sequences and Series Ex 9.1
• Chapter 9 Sequences and Series Ex 9.2
• Chapter 9 Sequences and Series Ex 9.3
• Chapter 9 Sequences and Series Ex 9.4
• Chapter 9 Sequences and Series Miscellaneous Exercise

PSEB 11th Class Math Book Pdf Chapter 10 Straight Lines

• Chapter 10 Straight Lines 10.1
• Chapter 10 Straight Lines 10.2
• Chapter 10 Straight Lines 10.3
• Chapter 10 Straight Lines Miscellaneous Exercise

PSEB Class 11 Maths Syllabus Chapter 11 Conic Sections

• Chapter 11 Conic Sections Ex 11.1
• Chapter 11 Conic Sections Ex 11.2
• Chapter 11 Conic Sections Ex 11.3
• Chapter 11 Conic Sections Ex 11.4
• Chapter 11 Conic Sections Miscellaneous Exercise

PSEB Class 11 Maths Book Pdf Download Chapter 12 Introduction to three Dimensional Geometry

• Chapter 12 Introduction to three Dimensional Geometry Ex 12.1
• Chapter 12 Introduction to three Dimensional Geometry Ex 12.2
• Chapter 12 Introduction to three Dimensional Geometry Ex 12.3
• Chapter 12 Introduction to three Dimensional Geometry Miscellaneous Exercise

PSEB Class 11 Maths Solutions Chapter 13 Limits and Derivatives

• Chapter 13 Limits and Derivatives Ex 13.1
• Chapter 13 Limits and Derivatives Ex 13.2
• Chapter 13 Limits and Derivatives Miscellaneous Exercise

11th Class Math Book PSEB Chapter 14 Mathematical Reasoning

• Chapter 14 Mathematical Reasoning Ex 14.1
• Chapter 14 Mathematical Reasoning Ex 14.2
• Chapter 14 Mathematical Reasoning Ex 14.3
• Chapter 14 Mathematical Reasoning Ex 14.4
• Chapter 14 Mathematical Reasoning Ex 14.5
• Chapter 14 Mathematical Reasoning Miscellaneous Exercise

Punjab Board Maths Book Class 11 Solutions Chapter 15 Statistics

• Chapter 15 Statistics Ex 15.1
• Chapter 15 Statistics Ex 15.2
• Chapter 15 Statistics Ex 15.3
• Chapter 15 Statistics Miscellaneous Exercise

PSEB 11 Class Math Book Pdf Chapter 16 Probability

• Chapter 16 Probability Ex 16.1
• Chapter 16 Probability Ex 16.2
• Chapter 16 Probability Ex 16.3
• Chapter 16 Probability Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3 Matrices Ex 3.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.3

Question 1.
Find the transpose of each of the following matrices:
(i) \(\left[\begin{array}{c}
5 \\
\frac{1}{2} \\
-1
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right]\)

(iii) \(\left[\begin{array}{ccc}
-1 & 5 & 6 \\
\sqrt{3} & 5 & 6 \\
2 & 3 & -1
\end{array}\right]\)
Solution.
(i) Let A = \(=\left[\begin{array}{c}
5 \\
\frac{1}{2} \\
-1
\end{array}\right]_{3 \times 1}\), then A’ = \(\left[5 \frac{1}{2}-1\right]_{1 \times 3}\).

(ii) Let A = \(\left[\begin{array}{cc}
1 & -1 \\
2 & 3
\end{array}\right]\), then A’ = \(\left[\begin{array}{cc}
1 & 2 \\
-1 & 3
\end{array}\right]\)

(iii) Let A = \(\left[\begin{array}{ccc}
-1 & 5 & 6 \\
\sqrt{3} & 5 & 6 \\
2 & 3 & -1
\end{array}\right]\), then A’ = \(\left[\begin{array}{ccc}
-1 & \sqrt{3} & 2 \\
5 & 5 & 3 \\
6 & 6 & -1
\end{array}\right]\).

Question 2.
If A = \(\) and B = \(\), then verify that
(i) (A + B) = A’ + B’
(ii) (A – B)’ = A’ – B’
Solution.
(i)

Hence, we have verified that (A + B)’ = A’ + B’

(ii)

 

Hence, we have verified that (A – B)’ = A’ – B’.

Question 3.
If A’ = \(\left[\begin{array}{cc}
3 & 4 \\
-1 & 2 \\
0 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]\), then verify that
(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’
Solution.
It is known that A = (A’)’
Therefore, we have
A = \(\left[\begin{array}{cc}
3 & 4 \\
-1 & 2 \\
0 & 1
\end{array}\right]^{\prime}=\left[\begin{array}{ccc}
3 & -1 & 0 \\
4 & 2 & 1
\end{array}\right]\)

B = \(\left[\begin{array}{ccc}
-1 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]^{\prime}=\left[\begin{array}{cc}
-1 & 1 \\
2 & 2 \\
1 & 3
\end{array}\right]\)

(i) A + B = \(\left[\begin{array}{ccc}
3 & -1 & 0 \\
4 & 2 & 1
\end{array}\right]+\left[\begin{array}{ccc}
-1 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]=\left[\begin{array}{lll}
2 & 1 & 1 \\
5 & 4 & 4
\end{array}\right]\)

Thus, we have verified that (A + B)’ = A’ + B’

(ii)

Thus, we have verified that (A – B)’ = A’ – B’.

Question 4.
If A’ = \(\left[\begin{array}{cc}
-\mathbf{2} & \mathbf{3} \\
\mathbf{1} & \mathbf{2}
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
-1 & 0 \\
1 & 2
\end{array}\right]\), then find (A + 2B)’.
Solution.
We know that A = (A’)’

Question 5.
For the matrices A and B, verify that (AB)’ = B’A’, where
(i) A = \(\left[\begin{array}{c}
1 \\
-4 \\
3
\end{array}\right]\), B = [- 1 2 1]
(ii) A = \(\left[\begin{array}{l}
\mathbf{0} \\
\mathbf{1} \\
\mathbf{2}
\end{array}\right]\), B = [1 5 7].
Solution.
(i)

B’A’ = \(\left[\begin{array}{c}
-1 \\
2 \\
1
\end{array}\right]\left[\begin{array}{lll}
1 & -4 & 3
\end{array}\right]=\left[\begin{array}{ccc}
-1 & 4 & -3 \\
2 & -8 & 6 \\
1 & -4 & 3
\end{array}\right]\)
Hence, we have verified that (AB)’ = B’A’.

(ii)

Hence, we have verified that (AB)’ = B’A’.

Question 6.
(i) If A = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\), then verify that A’A = I.

(ii) If A = \(\left[\begin{array}{cc}
\sin \alpha & \cos \alpha \\
-\cos \alpha & \sin \alpha
\end{array}\right]\), then verify that A’A = I.
Solution.

Hence, we have verified that A’A = I.

(ii) Given, A = \(\left[\begin{array}{cc}
\sin \alpha & \cos \alpha \\
-\cos \alpha & \sin \alpha
\end{array}\right]\)

∴ A’ = \(\left[\begin{array}{cc}
\sin \alpha & -\cos \alpha \\
\cos \alpha & \sin \alpha
\end{array}\right]\)

Hence, we have verified that A’A = I.

Question 7.
(i) Show that the matrix A = \(\left[\begin{array}{rrr}
1 & -1 & 5 \\
-1 & 2 & 1 \\
5 & 1 & 3
\end{array}\right]\) is a symmetric matrix.

(ii) Show that the matrix A = \(\left[\begin{array}{rrr}
0 & 1 & -1 \\
-1 & 0 & 1 \\
1 & -1 & 0
\end{array}\right]\) is a skew symmetric matrix.
Solution.
We have A’ = \(=\left[\begin{array}{rrr}
1 & -1 & 5 \\
-1 & 2 & 1 \\
5 & 1 & 3
\end{array}\right]\) = A
Hence, A is a symmetric matrix.

(ii) We have, A’ = \(\left[\begin{array}{rrr}
0 & -1 & 1 \\
1 & 0 & -1 \\
-1 & 1 & 0
\end{array}\right]\)

= – \(\left[\begin{array}{rrr}
0 & 1 & -1 \\
-1 & 0 & 1 \\
1 & -1 & 0
\end{array}\right]\) = – A
∴ A’ = – A
Hence, A’ is a symmetric matrix.

Question 8.
For the matrix A = \(\left[\begin{array}{ll}
1 & 5 \\
6 & 7
\end{array}\right]\), verify that
(i) (A + A’)’ is a symmetric matrix.
(ii) (A – A’) is a skew symmetric matrix.
Solution.
We have, A’ = \(\left[\begin{array}{ll}
1 & 6 \\
5 & 7
\end{array}\right]\)

(i) A + A’ = \(\left[\begin{array}{ll}
1 & 5 \\
6 & 7
\end{array}\right]+\left[\begin{array}{ll}
1 & 6 \\
5 & 7
\end{array}\right]=\left[\begin{array}{cc}
2 & 11 \\
11 & 14
\end{array}\right]\)

(A + A’)’ = \(\left[\begin{array}{cc}
2 & 11 \\
11 & 14
\end{array}\right]\) = A + A’
Hence, (A + A’)’ is a symmetric matrix.

(ii) A – A’ = \(\left[\begin{array}{ll}
1 & 5 \\
6 & 7
\end{array}\right]-\left[\begin{array}{ll}
1 & 6 \\
5 & 7
\end{array}\right]=\left[\begin{array}{rr}
0 & -1 \\
1 & 0
\end{array}\right]\)

(A – A’)’ = \(\left[\begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array}\right]=-\left[\begin{array}{rr}
0 & -1 \\
1 & 0
\end{array}\right]\) = -(A – A’).
Thus, (A – A’) is a skew symmetric matrix.

Question 9.
Find \(\frac{1}{2}\) (A + A’) and \(\frac{1}{2}\) (A – A’) when A = \(\left[\begin{array}{ccc}
0 & \boldsymbol{a} & \boldsymbol{b} \\
-\boldsymbol{a} & \mathbf{0} & \boldsymbol{c} \\
-\boldsymbol{b} & -\boldsymbol{c} & \mathbf{0}
\end{array}\right]\).
Solution.

Question 10.
Express the following matrices as the sum of a symmetric and a skew-symmetric matrix.
(i) \(\left[\begin{array}{rr}
\mathbf{3} & \mathbf{5} \\
\mathbf{1} & -\mathbf{1}
\end{array}\right]\)

(ii) \(\left[\begin{array}{rrr}
6 & -2 & 2 \\
-2 & 3 & -1 \\
2 & -1 & 3
\end{array}\right]\)

(iii) \(\left[\begin{array}{rrr}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\)

(iv) \(\left[\begin{array}{cc}
1 & 5 \\
-1 & 2
\end{array}\right]\)
Solution.

Let, Q = \(\frac{1}{2}\) (A – A’)

= \(\frac{1}{2}\) \(\left[\begin{array}{cc}
0 & 4 \\
-4 & 0
\end{array}\right]=\left[\begin{array}{cc}
0 & 2 \\
-2 & 0
\end{array}\right]\)

Now, Q’ = \(\left[\begin{array}{cc}
0 & -2 \\
2 & 0
\end{array}\right]\) = – Q
Thus, Q = \(\frac{1}{2}\) (A – A’) is a skew symmetric matrix.
Representing A as the sum of P and Q
P + Q = \(\left[\begin{array}{rr}
3 & 3 \\
3 & -1
\end{array}\right]+\left[\begin{array}{rr}
0 & 2 \\
-2 & 0
\end{array}\right]=\left[\begin{array}{rr}
3 & 5 \\
1 & -1
\end{array}\right]\) = A

 

(ii)

(iii)

Thus, Q = \(\frac{1}{2}\) (A – A’) is a skew-symmetric matrix.
P + Q = \(\left[\begin{array}{ccc}
3 & \frac{1}{2} & -\frac{5}{2} \\
\frac{1}{2} & -2 & -2 \\
-\frac{5}{2} & -2 & 2
\end{array}\right]+\left[\begin{array}{ccc}
0 & \frac{5}{2} & \frac{3}{2} \\
-\frac{5}{2} & 0 & 3 \\
-\frac{3}{2} & -3 & 0
\end{array}\right]=\left[\begin{array}{ccc}
3 & 3 & -1 \\
-2 & -2 & 1 \\
-4 & -5 & 2
\end{array}\right]\) = A.

(iv) Let A = \(\left[\begin{array}{rr}
1 & 5 \\
-1 & 2
\end{array}\right]\), then A’ = \(\left[\begin{array}{cc}
1 & -1 \\
5 & 2
\end{array}\right]\)

Now, A + A’ = \(\left[\begin{array}{cc}
1 & 5 \\
-1 & 2
\end{array}\right]+\left[\begin{array}{cc}
1 & -1 \\
5 & 2
\end{array}\right]=\left[\begin{array}{cc}
2 & 4 \\
4 & 4
\end{array}\right]\)

Let P = \(\frac{1}{2}\) (A + A’) = \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]\)

Now, p’ = \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]\) = p

Thus, P = \(\frac{1}{2}\) (A + A’) is a symmetric matrix.

Now, A – A’ = \(\left[\begin{array}{cc}
1 & 5 \\
-1 & 2
\end{array}\right]-\left[\begin{array}{cc}
1 & -1 \\
5 & 2
\end{array}\right]=\left[\begin{array}{cc}
0 & 6 \\
-6 & 0
\end{array}\right]\)
Let Q = \(\frac{1}{2}\) (A – A’) = \(\left[\begin{array}{cc}
0 & 3 \\
-3 & 0
\end{array}\right]\)

Now, Q’ = \(\left[\begin{array}{cc}
0 & -3 \\
3 & 0
\end{array}\right]\) = – Q
Thus, Q = \(\frac{1}{2}\) (A – A’) is a skew symmetric matrix.
Representing A as the sum of P and Q:
P + Q = \(\left[\begin{array}{ll}
1 & 2 \\
2 & 2
\end{array}\right]+\left[\begin{array}{cc}
0 & 3 \\
-3 & 0
\end{array}\right]=\left[\begin{array}{cc}
1 & 5 \\
-1 & 2
\end{array}\right]\) = A.

Direction (11 – 12) : Choose the correct answer in the following questions.

Question 11.
If A and B are symmetric matrices of same order, then AB – BA is a
(A) skew-symmetric matrix
(B) symmetric matrix
(C) zero matrix
(D) identity matrix
Solution.
A and B are symmetric matrices, therefore we have
A’ = A and B’ = B …………..(i)
Consider (AB – BA)’ = (AB)’ – (BA)’ [∵ (A – B)’ = A’ – B’]
= B’A’ – A’B’ [v (AB/= B’A’] [∵ (AB)’ = B’A’]
= BA – AB [FromEq. (i)]
= – (AB – BA)
∴ (AB – BA) = – (AB – BA)
Thus, (AB – BA) is a skew-symmetric matrix.
Hence, the correct answer is (A).

Question 12.
If A = \(\), then A + A’ = I, if the value of α is
(A) \(\frac{\pi}{6}\)

(B) \(\frac{\pi}{3}\)

(C) π

(D) \(\frac{3 \pi}{2}\)
Solution.
We have, A = \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]\)

⇒ A’ = \(\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]\)

Given, A + A’ = I
∴ \(\left[\begin{array}{cc}
\cos \alpha & -\sin \alpha \\
\sin \alpha & \cos \alpha
\end{array}\right]+\left[\begin{array}{cc}
\cos \alpha & \sin \alpha \\
-\sin \alpha & \cos \alpha
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)

⇒ \(\left[\begin{array}{cc}
2 \cos \alpha & 0 \\
0 & 2 \cos \alpha
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)

On comparing the corresponding elements of these two matrices, we have
2 cos α = 1
⇒ cos α = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
∴ α = \(\frac{4}{4}\)
Hence, the correct answer is (B).

Punjab State Board PSEB 11th Class Chemistry Important Questions Chapter 3 Classification of Elements and Periodicity in Properties Important Questions and Answers.

PSEB 11th Class Chemistry Important Questions Chapter 3 Classification of Elements and Periodicity in Properties

Very Short Answer Type Questions

Question 1.
Which properties of the elements depend on’ the electronic configuration of the atoms and which do not?
Answer:
Chemical and many physical properties of the elements depends on the electronic configuration of the atoms, whereas the nuclear properties do not.

Question 2.
Write the number designation of a group that has 2 electrons beyond a noble gas configuration.
Answer:
The number designation of a group that has 2 electrons beyond a noble gas configuration will be 2 which means it will belong to group 2 of periodic table.

Question 3.
Why is it more logical to call the atomic radius as the effective atomic radius?
Answer:
This is because the size of atom is very small and it has no sharp boundaries.

Question 4.
A boy has reported the radii of Cu, Cu⁺ and Cu²⁺ as 0.096 nm, 0.122 nm and Question072 nm respectively. However, it has been noticed that he interchanged the values by mistake. Assign the correct values to different species.
Answer:
Cu [0.122 nm], Cu⁺ [0.096 nm], Cu²⁺ [0.072 nm].
∵ Size ∝ \(\frac{1}{\text { positive charge }}\)

Question 5.
Atomic radii of fluorine is 72 pm where as atomic radii of neon is 160 pm. Why? [NCERT Exemplar]
Answer:
Atomic radius of F is expressed in terms of covalent radius while, atomic radius of neon is usually expressed in terms of van der Waals’ radius, van der Waals’ radius of an element is always larger than its covalent radius.
Therefore, atomic radius of F is smaller than atomic radius of Ne (F = 72 pm, Ne = 160 pm)

Question 6.
Arrange the following elements in order of decreasing electron gain enthalpy : B, C, N, O.
Answer:
N has positive electron gain enthalpy while all others have negative electron gain enthalpies. Since size decreases on moving from B → C → O, therefore, electron gain enthalpies become more and more negative from B → C → O. Thus, the overall decreasing order of electron gain enthalpies is N, B, C, O.

Question 7.
Which of the following atoms would most likely form an anion (i) Be, (ii) Al, (iii) Ga, (iv) I ?
Answer:
I, because of high electron gain enthalpy, it can accept an electron readily to form an anion F < Cl < Br > I.

Question 8.
Explain why chlorine can be converted into chloride ion more easily as compared to fluoride ion from fluorine.
Answer:
Electron gain enthalpy of Cl is more negative than that of F.

Question 9.
Among alkali metals which element do you expect to be least electronegative and why? [NCERT Exemplar]
Answer:
On moving down the group, electronegativity decreases because atomic size increases. Fr has the largest size, therefore it is least electronegative.

Question 10.
Arrange the following elements in the increasing order of non-metallic character. B, C, Si, N, F
Answer:
The given non-metals are arranged in the increasing order of non-metallic character as follows:

Short Answer Type Questions

Question 1.
What would be IUPAC names and symbols for elements with atomic numbers 122, 127, 135, 149 and 150? .
Answer:
The roots 2, 7, 5, 9 and 0 are referred as bi, sept, pent, enn and nil respectively. Therefore, their names and symbol are

Z (Atomic number)	Name	Symbol
122	Unbibium	Ubb
127	Unbiseptium	Ubs
135	Untripentium	Dtp
149	Unquadennium	Uqe
150	Unpentnilium	Upn

Question2.
All transition elements are d-block elements, but all d-block elements are not transition elements. Explain.
Answer:
Elements in which the last electron enters in the d-orbitals, are called d-block elements or transition elements. These elements have the general outer electronic configuration (n – 1)d^1-10ns^0-2 Zn, Cd and Hg having the electronic configuration, (n – l1)d¹⁰ns² do not show most of the properties of transition elements. The d-orbitals in these elements are completely filled in the ground state as well as in their common oxidation states. Therefore, they are not regarded as transition elements. Thus, on the basis of properties, all transition elements are d-block elements but on the basis of electronic configuration, all d-block elements are not transition elements.

Question 3.
Arrange the elements N, P, O and S in the order of
(i) increasing first ionisation enthalpy.
(ii) increasing non-metallic character.
Give reason for the arrangement assigned.
Answer:

	Group 15	Group 16
2nd period	N	0
3rd period	P	S

(i) Ionisation enthalpy of nitrogen (₇N = 1s², 2s², 2p³) is greater than oxygen (₈O = 1s² , 2s² , 2p⁴ ) due to extra stable half-filled 2p-orbitals. Similarly, ionisation enthalpy of phosphorus (₁₅P = 1s², 2s², 2p⁶, 3s², 3p³) is greater than sulphur (₁₆S = 1s², 2x², 2p⁶, 3s², 3p⁴).
On moving down the group, ionisation enthalpy decreases with increasing atomic size. So, the increasing order of first ionisation enthalpy is S < P < O < N.

(ii) Non-metallic character across a period (left to right) increases but on moving down the group it decreases. So, the increasing order of non-metallic character is P < S < N < 0.

Question 4.
What do you understand by exothermic reaction and endothermic reaction? Give one example of each type.
Answer:
Exothermic reactions : Reactions which are accompanied by evolution of heat are called exothermic reactions. The quantity of heat produced is shown either along with the products with a ‘+’ sign or in terms if ΔH with a sign, e.g.,

C(s) + O₂(g) → CO₂(g) + 393.5 kJ
H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l) ΔH = -285.8 kJ mol^-1

Endothermic reactions : Reactions which proceed with absorption of heat are called endothermic reactions. The quantity of heat absorbed is shown either alongwith the products with a sign or in terms of ΔH with a ‘-‘ sign, e.g.,

C(s) + H₂O(g) → CO(g) + H₂(g) -131.4 kJ
N₂(g) + 3H₂(g) → 2NH₃(g); ΔH = +92.4 kJ mol^-1

Question5.
How does the metallic and non-metallic character vary on moving from left to right in a period?
Answer:
As we move from left to right in a period, the number of valence electrons increases by one at each succeeding element but the number of shells remains same. Due to this, effective nuclear charge increases.

More is the effective nuclear charge, more is the attraction between nuclei and electron.
Hence, the tendency of the element to lose electrons decreases, this results in decrease in metallic character.
Furthermore, the tendency of an element to gain electrons increases with increase in effective nuclear charge, so non-metallic character increases on moving from left to right in a period.

Long Answer Type Questions

Question 1.
Write the drawbacks in Mendeleev’s Periodic Table that led to its modification.
Answer:
The main drawbacks of Mendeleev’s Periodic Table are:
(i) Some elements having similar properties were placed in different groups whereas some elements having dissimilar properties were placed in the same group. For example alkali metals such as Li, Na, K, etc., (I A group) are grouped together with coinage metals such as Cu, Ag, Au (I B group) though their properties are quite different. Chemically similar elements such as Cu (I B group) and Hg (II B group) have been placed in different groups.

(ii) Some elements with higher atomic weights are placed before the elements with lower atomic weights in order to maintain the similar chemical nature of elements. For example,

(iii) Isotopes did not find any place in the Periodic Table. However, according to Mendeleev’s classification, these should be placed at different places in the Periodic Table.
(All the above three defects were however removed when modern periodic law based on atomic number was given.)

(iv) Position of hydrogen in the Periodic Table is not fixed but is
controversial. ,
(v) Position of elements of group VIII could not be made clear which have been arranged in three triads without any justification.
(vi) It could not explain the even and odd series in IV, V and VI long periods.
(vii) Lanthanides and actinides which were discovered later on, have not been given proper positions in the main frame of Periodic Table.

Question 2.
p-block elements form acidic, basic and amphoteric oxides. Explain each property by giving two examples and also write the reactions of these oxides with water.
Answer:
In p-block, when we move from left to right in a period, the acidic character of the oxides increases due to increase in electronegativity, e.g.,

(i) 2nd period
B₂O₃ < CO₂ < N₂O₃ acidic character increases.

(ii) 3rd period
Al₂O₃ < SiO₂ < P₄O₁₀ < SO₃ < Cl₂O₇ acidic character increases.
On moving down the group, acidic character decreases and basic character increases, e.g.,

(a) Nature of oxides of 13 group elements

(b) Nature of oxides of 15 group elements

Among the oxides of same element, higher the oxidation state of the element, stronger is the acid. e.g., SO₃ is a stronger acid than SO₂. B₂O₃ is weakly acidic and on dissolution in water, it forms orthoboric acid. Orthoboric acid does not act as a protonic acid (it does not ionise) but acts as a weak Lewis acid.

Al₂O₃ is amphoteric in nature. It is insoluble in water but dissolves in alkalies and react with acids.

Tl₂O is as basic as NaOH due to its lower oxidation state (+1).
Tl₂O + 2HCl → 2TlCl + H₂O

P₄O₁₀ on reaction with water gives orthophosporic acid.

Cl₂O₇ is strongly acidic in nature and on dissolution in water, it gives perchloric acid.

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Miscellaneous Exercise

Question 1.
Prove that the determinant \(\left|\begin{array}{ccc}
x & \sin \theta & \cos \theta \\
-\sin \theta & -x & 1 \\
\cos \theta & 1 & x
\end{array}\right|\) is independent of θ.
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
x & \sin \theta & \cos \theta \\
-\sin \theta & -x & 1 \\
\cos \theta & 1 & x
\end{array}\right|\)
On expanding to corresponding first row, we get
= x(- x² – 1) – sin θ (- x sin θ – cos θ) + cos θ(- sin θ + x cos θ)
= – x³ – x + x sin² θ + sinθ cos θ – sin θ cos θ + x cos² θ
= – x³ – x + x(sin² θ + cos² θ) [∵ sin² θ +cos² θ = 1]
= – x³ – x + x = – x³
Hence, ∆ is independent of θ.

Question 2.
Without expanding the determinant, prove that
\(\left|\begin{array}{lll}
a & a^{2} & b c \\
b & b^{2} & c a \\
c & c^{2} & a b
\end{array}\right|=\left|\begin{array}{ccc}
1 & a^{2} & a^{3} \\
1 & b^{2} & b^{3} \\
1 & c^{2} & c^{3}
\end{array}\right|\)
Solution.

Question 3.
Evaluate \(\left|\begin{array}{ccc}
\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\
-\sin \beta & \cos \beta & 0 \\
\sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha
\end{array}\right|\)
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\
-\sin \beta & \cos \beta & 0 \\
\sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha
\end{array}\right|\)

By expanding along C₃ we have
∆ = – sin α (- sin α sin² β – cos2 β sin α) + cos α (cos α cos2 β + cos α sin2 β)
= sin² α (sin² β + cos² β) + cos² α (cos² β + sin² β)
= sin² α (1) + cos² α (1)
= 1 [∵ sin² θ + cos² θ = 1].

Question 4.
If a, b and c are real numbers, and ∆ = \(\left|\begin{array}{lll}
b+c & c+a & a+b \\
c+a & a+b & b+c \\
a+b & b+c & c+a
\end{array}\right|\) = 0.
Show that, either a + b + c = 0 or a = b= c.
Solution.
Given ∆ = \(\left|\begin{array}{lll}
b+c & c+a & a+b \\
c+a & a+b & b+c \\
a+b & b+c & c+a
\end{array}\right|\)

By expanding along R1, we have
∆ = 2(a + b + c)(1) [(b – c) (c – b) – (b – a) (c – a)]
= 2 (a + b + c) [- b² – c² + 2bc – bc + ba + ac – a²]
= 2(a + b + c) [ab + bc + ca – a² – b² – c²]
It is given that ∆ = 0.
(a + b + c) [ab + bc + ca – a² – b² – c²] = 0
⇒ Either a + b + c = 0, or ab + bc + ca – a² – b² – c² = 0
Now, ab + bc + ca – a² – b² – c² = 0
⇒ – 2ab – 2bc – 2ca + 2a² + 2b² + 2c² = 0
⇒ (a – b)² + (b – c)² + (c – a)² = 0
⇒ (a – b)² = (b – c)² = (c – a)² = 0
[Since (a – b)², (b – c)² and (c – a)² are non – negative]
⇒ (a – b) = (b – c) = (c – a)
⇒ a = b = c
Hence, if ∆ = 0, then either a + b + c = 0 or a = b = c.

Question 5.
Solve the equation \(\left|\begin{array}{ccc}
x+a & x & x \\
x & x+a & x \\
x & x & x+a
\end{array}\right|\) = 0, a ≠ 0
Solution.

(3x + a) \(\left|\begin{array}{lll}
1 & 0 & 0 \\
x & a & 0 \\
x & 0 & a
\end{array}\right|\) = 0

(App1ying C₂ → C₂ – C₁ and C₃ → C₃ – C₁)
By expanding along R₁ we have
(3x + a) [1 × a²] = 0
⇒ a² (3x + a) = 0
But a ≠ 0
Therefore, 3x + a = 0
x = – \(\frac{a}{3}\)

Question 6.
Prove that \(\left|\begin{array}{ccc}
a^{2} & b c & a c+c^{2} \\
a^{2}+a b & b^{2} & a c \\
a b & b^{2}+b c & c^{2}
\end{array}\right|\) = 4a²b²c²
Solution.

By expanding along R₃, we have
∆ = 2ab²c [a(c – a) + a(a +c)]
= 2ab²c[ac – a² + a² + ac]
= 2ab²c(2ac)
= 4a²b²c²
Hence, the given result is proved.

Question 7.
If A^-1 = \(\left[\begin{array}{crr}
3 & -1 & 1 \\
-15 & 6 & -5 \\
5 & -2 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{rrr}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right]\), find (AB)^-1.
Solution.
We kncw that (AB)^-1 = B^-1A^-1 and A^-1 is known therefore, we proceed to find B^-1
Here, |B| = \(\left|\begin{array}{rrr}
1 & 2 & -2 \\
-1 & 3 & 0 \\
0 & -2 & 1
\end{array}\right|\)
= 1 (3 – 0) – 2(- 1 – 0) – 2 (2 – 0)
= 3 + 2 – 4 = 1 ≠ 0
Thus, B is non-singular.
Therefore, its inverse exists.
Cofactors of B are
B₁₁ = (3 – 0) = 3,
B₁₂ = – (- 1 – 0) = 1,
B₁₃ = (2 – 0) = 2,
B₂₁ = – (2 – 4) = – 2,
B₂₂ = 1 – 0 = 1,
B₂₃ = – (- 2 – 0) = 2,
B₃₁ = (0 + 6) = 6,
B₃₂ = – (0 – 2) =2,
B₃₃ = 3 + 2 = 5

Question 8.
Let A = \(\left[\begin{array}{rrr}
1 & -2 & 1 \\
-2 & 3 & 1 \\
1 & 1 & 5
\end{array}\right]\). verify that
(i) [adj A]^-1 = adj (A)^-1
(ii) (A^-1)^-1 = A
Solution.
Given, A = \(\left[\begin{array}{rrr}
1 & -2 & 1 \\
-2 & 3 & 1 \\
1 & 1 & 5
\end{array}\right]\)

∴ |A| = 1(5 – 1) + 2(- 10 – 1) + 1 (- 2 – 3) = 14 – 22 – 5 = – 13 ≠ 0
Thus, A is non-singular. Therefore its inverse exists.
Cofactors of A are
A₁₁ = 14,
A₁₂= 11,
A₁₃ = – 5
A₂₁ = 11,
A₂₂ = 4,
A₂₃ = – 3
A₃₁ = – 5
A₃₂ = – 3
A₃₃ = – 1

∴ adj (A) = \(\left[\begin{array}{ccc}
14 & 11 & -5 \\
11 & 4 & -3 \\
-5 & -3 & -1
\end{array}\right]\)

∴ A^-1 = \(\frac{1}{|A|}\) (adj A)
= \(-\frac{1}{13}\left[\begin{array}{ccc}
14 & 11 & -5 \\
11 & 4 & -3 \\
-5 & -3 & -1
\end{array}\right]=\frac{1}{13}\left[\begin{array}{ccc}
-14 & -11 & 5 \\
-11 & -4 & 3 \\
5 & 3 & 1
\end{array}\right]\)

(i) Let B = |adj A|
= 14 (- 4 – 9) – 11(- 11 – 15) – 5(- 33 + 20)
= 14(- 13) – 11(- 26) – 5(- 13)
= – 182 + 286 + 65 = 169 ≠ 0
Cofactors of B are:
B₁₁ = – 13,
B₁₂ = 26,
B₁₃ = – 13,
B₂₁ = 26,
B₂₂ = – 39,
B₂₃ = – 13
B₃₁ = – 13,
B₃₂ = – 13,
B₃₃ = – 65
∴ adj(adjA) = \(\left[\begin{array}{rrr}
-13 & 26 & -13 \\
26 & -39 & -13 \\
-13 & -13 & -65
\end{array}\right]\)
∴ B = [adj A]^-1
= \(\frac{1}{|\ {adj} A|}\) [adj(adj A)]

= \(\frac{1}{169}\left[\begin{array}{rrr}
-13 & 26 & -13 \\
26 & -39 & -13 \\
-13 & -13 & -65
\end{array}\right]=\frac{1}{13}\left[\begin{array}{rrr}
-1 & 2 & -1 \\
2 & -3 & -1 \\
-1 & -1 & -5
\end{array}\right]\) ……………..(i)

Cofactors of A^-1 are
A₁₁ = \(\frac{-13}{169}\)

A₁₂ = \(\frac{26}{169}\)

A₁₃ = \(\frac{-13}{169}\)

A₂₁ = \(\frac{26}{169}\)

A₂₂ = \(\frac{-39}{169}\)

A₂₃ = \(\frac{-13}{169}\)

A₃₁ = \(\frac{-13}{169}\)

A₃₂ = \(\frac{-13}{169}\)

A₃₃ = \(\frac{-65}{169}\)

= \(\frac{1}{169}\left[\begin{array}{ccc}
-13 & 26 & -13 \\
26 & -39 & -13 \\
-13 & -13 & -65
\end{array}\right]=\frac{1}{13}\left[\begin{array}{rrr}
-1 & 2 & -1 \\
2 & -3 & -1 \\
-1 & -1 & -5
\end{array}\right]\) ……………(ii)

From Eqs. (i) and (ii) we get
[adj A]^-1 = adj (A^-1).

(ii) We have shown that
A^-1 = \(\frac{1}{13}\left[\begin{array}{rrr}
-14 & -11 & 5 \\
-11 & -4 & 3 \\
5 & 3 & 1
\end{array}\right]\)

and adj A^-1 = \(\frac{1}{13}\left[\begin{array}{rrr}
-1 & 2 & -1 \\
2 & -3 & -1 \\
-1 & -1 & -5
\end{array}\right]\)
Now, |A^-1| = \(\left(\frac{1}{13}\right)^{3}\) [- 14 × (- 13) + 11 × (- 26) + 5 × (- 13)]
= \(\left(\frac{1}{13}\right)^{3}\) × (- 169) = \(-\frac{1}{13}\)

∴ (A^-1)^-1 = \(\frac{\ {adj} A^{-1}}{\left|A^{-1}\right|}\)

= \(\frac{1}{\left(-\frac{1}{13}\right)} \times \frac{1}{13}\left[\begin{array}{rrr}
-1 & 2 & -1 \\
2 & -3 & -1 \\
-1 & -1 & -5
\end{array}\right]\)

= \(\left[\begin{array}{rrr}
1 & -2 & 1 \\
-2 & 3 & 1 \\
1 & 1 & 5
\end{array}\right]\) = A
∴ (A^-1)^-1 = A.

Question 9.
Evaluate \(\left|\begin{array}{ccc}
x & y & x+y \\
y & x+y & x \\
x+y & x & y
\end{array}\right|\).
Solution.

By expanding along R₁, we have
∆ = 2 (x + y) [- x² + y (x – y)]
= – 2 (x + y) (x² + y² – yx)
= – 2(x³ + y³).

Question 10.
Evaluate \(\left|\begin{array}{ccc}
1 & x & y \\
1 & x+y & y \\
1 & x & x+y
\end{array}\right|\).
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
1 & x & y \\
1 & x+y & y \\
1 & x & x+y
\end{array}\right|\)

App1ying R₂ → R₂ – R₁ and R₃ → R₃ – R₁

∆ = \(\left|\begin{array}{lll}
1 & x & y \\
0 & y & 0 \\
0 & 0 & x
\end{array}\right|\)
By expanding along C₁, we have
∆ = 1(xy – 0) = xy.

DirectIon (11 – 15):
Using ptoperties of determinants, prove that following questions

Question 11.
\(\left|\begin{array}{lll}
\alpha & \alpha^{2} & \beta+\gamma \\
\beta & \beta^{2} & \gamma+\alpha \\
\gamma & \gamma^{2} & \alpha+\beta
\end{array}\right|\) = (β – γ) (γ – α) (α – β) (α + β + γ)
Solution.

By expanding along R₃, we have
= (β – α) (γ – α) [- (γ – β) (- α – β – γ)]
= (β – α) (γ – α) (γ – β)(α + β + γ)
= (α – β) (β – γ) (γ – α) (α + β + γ)
Hence, the given result is proved.

Question 12.
\(\left|\begin{array}{lll}
x & x^{2} & 1+p x^{3} \\
y & y^{2} & 1+p y^{3} \\
z & z^{2} & 1+p z^{3}
\end{array}\right|\) = (1 + pxyz) (x – y) (y – z) (z – x)
Solution.
Let ∆ = \(\left|\begin{array}{lll}
x & x^{2} & 1+p x^{3} \\
y & y^{2} & 1+p y^{3} \\
z & z^{2} & 1+p z^{3}
\end{array}\right|\)
App1ying R₂ → R₂ – R₁ and R₃ → R₃ – R₁

By expanding along R₃, we have
∆ = (x – y) (y – z) (z – x) [(- 1)(p) (xy² + x³ + x²y) + 1 + px³ + p (x + y + z) (xy)]
= (x – y) (y – z) (z – x) [- pxy² – px³ – px²y + 1 + px³ + px²y + pxy² + pxyz]
= (x – y) (y – z) (z – x) (1 + pxyz)
Hence, the given result is proved.

Question 13.
\(\left|\begin{array}{ccc}
3 a & -a+b & -a+c \\
-b+a & 3 b & -b+c \\
-c+a & -c+b & 3 c
\end{array}\right|\) = 3 (a + b + c) (ab + bc + ca)
Solution.

∆ = (a + b + c) \(\left|\begin{array}{ccc}
1 & -a+b & -a+c \\
0 & 2 b+a & a-b \\
0 & a-c & 2 c+a
\end{array}\right|\)
By expanding along C₁, we have
∆ = (a + b + c) [(2b + a) (2c + a) – (a – b) (a – c)]
= (a + b + c) [4bc + 2ab + 2ac + a² – a² + ac + ba – bc]
= (a + b + c) (3ab + 3bc + 3ac)
= 3(a + b + c)(ab + bc + ca)
Hence, the given result is proved.

Question 14.
\(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
2 & 3+2 p & 4+3 p+2 q \\
3 & 6+3 p & 10+6 p+3 q
\end{array}\right|\) = 1
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
2 & 3+2 p & 4+3 p+2 q \\
3 & 6+3 p & 10+6 p+3 q
\end{array}\right|\)
Applying R₂ → R₂ 2R₁ and R₃ → R₃ – 3 R₁, we have

∆ = \(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
0 & 1 & 2+p \\
0 & 3 & 7+3 p
\end{array}\right|\)
Applying R₃ → R₃ – 3 R₂, we have

∆ = \(\left|\begin{array}{ccc}
1 & 1+p & 1+p+q \\
0 & 1 & 2+p \\
0 & 0 & 1
\end{array}\right|\)

By expanding along C₁, we have = 1 (1 – 0) = 1.

Question 15.
\(\left|\begin{array}{ccc}
\sin \alpha & \cos \alpha & \cos (\alpha+\delta) \\
\sin \beta & \cos \beta & \cos (\beta+\delta) \\
\sin \gamma & \cos \gamma & \cos (\gamma+\delta)
\end{array}\right|\) = 0
Solution.

Taking common cos δ from C₃ in first determinant and taking common – sin δ from C₃ in second determinant
∆ = \(\cos \delta\left|\begin{array}{lll}
\sin \alpha & \cos \alpha & \cos \alpha \\
\sin \beta & \cos \beta & \cos \beta \\
\sin \gamma & \cos \gamma & \cos \gamma
\end{array}\right|-\sin \delta\left|\begin{array}{ccc}
\sin \alpha & \cos \alpha & \sin \alpha \\
\sin \beta & \cos \beta & \sin \beta \\
\sin \gamma & \cos \gamma & \sin \gamma
\end{array}\right|\)
∆ = cos δ . 0 – sin δ . 0 = 0
[Since, C₂ and C₃ in first determinant C₁ and C₃ in second determinant are identical so values of determinants are zero.]
Hence, the given result is proved.

Question 16.
Solve the system of the following equations
\(\frac{2}{x}+\frac{3}{y}+\frac{10}{z}\) = 4; \(\frac{4}{x}-\frac{6}{y}+\frac{5}{z}\) = 1; \(\frac{6}{x}+\frac{9}{y}-\frac{20}{x}\) = 2
Solution.
Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q, \(\frac{1}{z}\) = r.
Then, the given system of equation is as follows:
2p + 3q + 10r = 4, 4p – 6q + 5r = 1, 6p + 9q – 20 = 2.
This system can be written in the form of AX = B, where

A = \(\left[\begin{array}{ccc}
2 & 3 & 10 \\
4 & -6 & 5 \\
6 & 9 & -20
\end{array}\right]\), X = \(\left[\begin{array}{l}
p \\
q \\
r
\end{array}\right]\) and B = \(\left[\begin{array}{l}
4 \\
1 \\
2
\end{array}\right]\)

Now, |A| = 2(120 – 45) – 3(- 80 – 30) + 10 (36 + 36)
= 150 + 330 + 720 = 1200
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 75,
A₁₂ = 110,
A₁₃ = 72,
A₂₁ = 150,
A₂₂ = – 100,
A₂₃ = 0,
A₃₁ = 7,
A₃₂ = 30,
A₃₃ = – 24

= \(\frac{1}{1200}\left[\begin{array}{c}
300+150+150 \\
440-100+60 \\
288+0-48
\end{array}\right]=\frac{1}{1200}\left[\begin{array}{c}
600 \\
400 \\
240
\end{array}\right]=\left[\begin{array}{l}
\frac{1}{2} \\
\frac{1}{3} \\
\frac{1}{5}
\end{array}\right]\)

∴ p = \(\frac{1}{2}\), q = \(\frac{1}{3}\) and r = \(\frac{1}{5}\)
⇒ \(\frac{1}{x}=\frac{1}{2}\), \(\frac{1}{y}=\frac{1}{3}\), \(\frac{1}{z}=\frac{1}{5}\)
Hence x = 2, y = 3 and z = 5.

Direction (17 – 19): Choose the correct answer in the following questions.

Question 17.
If a, b and c are in AP., then the determinant \(\left|\begin{array}{lll}
x+2 & x+3 & x+2 a \\
x+3 & x+4 & x+2 b \\
x+4 & x+5 & x+2 c
\end{array}\right|\) is
(A) 0
(B) 1
(C) x
(D) 2x
Solution.

Question 18.
If x, y and z are non-zero real numbers, then the inverse of matrix A = \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\) is
(A) \(\left[\begin{array}{ccc}
x^{-1} & 0 & 0 \\
0 & y^{-1} & 0 \\
0 & 0 & z^{-1}
\end{array}\right]\)

(B) xyz \(\left[\begin{array}{ccc}
x^{-1} & 0 & 0 \\
0 & y^{-1} & 0 \\
0 & 0 & z^{-1}
\end{array}\right]\)

(C) \(\frac{1}{x y z}\left[\begin{array}{ccc}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\)

(D) \(\frac{1}{x y z}\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)
solution.
Given, A = \(\left[\begin{array}{lll}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & z
\end{array}\right]\)
∴ |A| = x (yz – 0) = xyz ≠ 0
(∵ x, y, z are non-zero)
Cofactors of A are
A₁₁ = yz,
A₁₂ = 0,
A₁₃ = 0
A₂₁ = 0,
A₂₂ = xz,
A ₂₃= 0
A₃₁ = 0,
A₃₂ = 0,
A₃₃ = xy

Hence, the correct answer is (A).

Question 19.
Let A = \(\left[\begin{array}{ccc}
1 & \sin \theta & 1 \\
-\sin \theta & 1 & \sin \theta \\
-1 & -\sin \theta & 1
\end{array}\right]\), where 0 ≤ θ ≤ 2π, then
(A) Det (A) = 0
(B) Det (A) ∈ (2, ∞)
(C) Det (A) ∈(2, 4)
(D)Det (A) ∈ [2, 4]
Solution.
Given, A = \(\left[\begin{array}{ccc}
1 & \sin \theta & 1 \\
-\sin \theta & 1 & \sin \theta \\
-1 & -\sin \theta & 1
\end{array}\right]\)

∴ |A| = 1 (1 + sin² θ) – sin θ (- sin θ + sin θ) – 1 (sin² θ + 1)
= 1 + sin² θ + sin² θ + 1
= 2 + 2 sin² θ
= 2 (1 + sin² θ)
Now, 0 ≤ θ ≤ 2π
= 0 ≤ sin θ ≤ 1
= 0 ≤ sin² θ ≤ 1
= 1 ≤ 1 + sin² θ ≤ 2
= 2 ≤ 2 (1 + sin² θ) ≤ 4
∴ Det (A) ∈ [2, 4]
Hence, the correct answer is (D).

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.3

Question 1.
Find area of the triangle with vertices at the point given in each of the following:
(i) (a, 0), (6, 0), (4, 3)
(ii) (2, 7), (1, 1), (10, 8)
(iii) (- 2, – 3), (3, 2), (- 1, – 8)
Solution.
(i) The area of the triangle with vertices (1, 0), (6, 0) and (4, 3) is given by the relation,
∆ = \(\frac{1}{2}\) \(\left|\begin{array}{lll}
1 & 0 & 1 \\
6 & 0 & 1 \\
4 & 3 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [1 (0 – 3) – 0 (6 – 4) + 1 (18 – 0)]
= \(\frac{1}{2}\) [- 3 + 18]
= \(\frac{15}{2}\) sq. unit.

(ii) The area of the triangle with vertices (2, 7), (1,1) and (10,8), is given by the relation,
∆ = \(\frac{1}{2}\) \(\left|\begin{array}{ccc}
2 & 7 & 1 \\
1 & 1 & 1 \\
10 & 8 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [2(1 – 8) – 7(1 – 10) + 1(8 – 10)]
= \(\frac{1}{2}\) [2(- 7) – 7 (- 9) + 1 (- 2)]
= \(\frac{1}{2}\) [- 14 + 63 – 2]
= \(\frac{1}{2}\) [- 16 + 63]
= \(\frac{47}{2}\) sq. unit

(iii) The area of the triangle with vertices (- 2, – 3), (3, 2) and (- 1, – 8) is given by the relation,
∆ = \(\frac{1}{2}\) \(\left|\begin{array}{ccc}
-2 & -3 & 1 \\
3 & 2 & 1 \\
-1 & -8 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [- 2(2 + 8) + 3(3 + 1) + 1(- 24 + 2)]
= \(\frac{1}{2}\) [- 2 (10) + 3(4) + 1 (- 22)]
= \(\frac{1}{2}\) [- 20 + 12 – 22]
= – \(\frac{30}{2}\)
= -15 sq. unit.
Hence, the area of the triangle is |- 15 | = 15 sq. unit.

Question 2.
Show that points A(a, b + c), B(b, c + a), C(c, a + b) are collinear.
Solution.
Area of ∆ABC is given by the relation, ∆ = \(\frac{1}{2}\) \(\left|\begin{array}{ccc}
a & b+c & 1 \\
b & c+a & 1 \\
c & a+b & 1
\end{array}\right|\)

= \(\frac{1}{2}\) \(\left|\begin{array}{ccc}
a & b+c & 1 \\
b-c & a-b & 0 \\
c-a & a-c & 0
\end{array}\right|\)
(Applying R₂ → R₂ – R₁ and R → R₃ – R₁)
= \(\frac{1}{2}\) (a – b) (c – a) \(\left|\begin{array}{ccc}
a & b+c & 1 \\
-1 & 1 & 0 \\
1 & -1 & 0
\end{array}\right|\)

= \(\frac{1}{2}\) (a – b) (c – a) \(\left|\begin{array}{ccc}
a & b+c & 1 \\
-1 & 1 & 0 \\
0 & 0 & 0
\end{array}\right|\) = 0
(Applying R₃ → R₃ + R₂)
Thus, the area of the triangle formed by points A, B and C is zero.
Hence, the points A, B and C are collinear.

Question 3.
Find the value of k, if area of triangle is 4 sq. units and vertices are
(i) (k, 0), (4, 0), (0, 2)
(ii) (- 2, 0), (0, 4), (0, k)
Solution.
(i) The area of the triangle with vertices (k, 0), (4,0) and (0, 2) is given by the relation,
∆ = \(\frac{1}{2}\) \(\left|\begin{array}{lll}
k & 0 & 1 \\
4 & 0 & 1 \\
0 & 2 & 1
\end{array}\right|\) = 4

= \(\frac{1}{2}\) [k(0 – 2) – 0 (4 – 0) + 1 (8 – 0)] = 4
∴ – k + 4 = ± 4
When – k + 4 = – 4, then k = 8
When – k + 4 = 4, then k = 0
Hence, k = 0, 8.

(ii) The area of the triangle with vertices (- 2, 0), (0, 4) and (0, k) is given by the relation,
∆ = \(\frac{1}{2}\) \(\left|\begin{array}{ccc}
-2 & 0 & 1 \\
0 & 4 & 1 \\
0 & k & 1
\end{array}\right|\) = 4
∴ k – 4 = ± 4
When k – 4 = – 4, then k = 0
When k – 4 = 4, then k = 8
Hence, k = 0, 8.

Question 4.
(i) Find the equation of the line joining (1, 2) and (3, 6) using determinants.
(ii) Find the equation of the line joining (3, 1) and (9, 3) using determinants.
Solution.
(i) LetP(x, y) be any point on the line joining points A (1, 2) and B (3, 6).
Then, the points A, B and P are collinear. Therefore, the area of triangle ABP will be zero.
∴ \(\frac{1}{2}\) \(\left|\begin{array}{lll}
1 & 2 & 1 \\
3 & 6 & 1 \\
x & y & 1
\end{array}\right|\) = 0
⇒ 6 – y – 6 + 2x + 3y – 6x = 0
⇒ 2y – 4x = 0
⇒ 2x – y = 0
Hence, the equation of the line joining the given points is 2x – y = 0.

(ii) Let P (x, y) be any point on the line joining points A (3, 1) and B (9, 3).
Then, the points A, B and P are collinear.
Therefore, the area of triangle ABP will be zero.
∴ \(\frac{1}{2}\) \(\left|\begin{array}{lll}
3 & 1 & 1 \\
9 & 3 & 1 \\
x & y & 1
\end{array}\right|\) = 0
⇒ \(\frac{1}{2}\) [3 (3 – y) – 1(9 – x) + 1 (9y – 3x)] = 0
⇒ 9 – 3y – 9 + x + 9y – 3x = 0
⇒ 6y – 2x = 0
⇒ x – 3y = 0
Hence, the equation of the line joining the given points is x – 3y = 0.

Question 5.
If area of triangle is 35 sq. units with vertices (2, – 6), (5, 4) and (k, 4). Then, k is
(A) 12
(B) – 2
(C) – 12, – 2
(D) 12, – 2
Solution.
The area of the triangle with vertices (2, – 6), (5, 4), and (k, 4) is given by the relation.
∆ = \(\frac{1}{2}\) \(\left|\begin{array}{ccc}
2 & -6 & 1 \\
5 & 4 & 1 \\
k & 4 & 1
\end{array}\right|\)
= \(\frac{1}{2}\) [2 (4 – 4) + 6 (5 – k) +1 (20 – 4k)]
= \(\frac{1}{2}\) [30 – 6k + 20 – 4k]
= \(\frac{1}{2}\) [50 – 10k]
= 25 – 5k
It is given that the area of the triangle is ± 35.
Therefore, we have
⇒ 25- 5k = ± 35
⇒ 5(5 – k) = ± 35
⇒ 5 – k = ±7
When 5 – k = – 7, then k = 5 + 7 = 12
When 5 – k = 7, then k = 5 – 7 = – 2
Hence, k = 12, – 2.
The correct answer is (D).

Punjab State Board PSEB 12th Class Physical Education Book Solutions Chapter 3 ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿੱਚ ਕਿੱਤੇ ਅਤੇ ਖੇਡ ਅਵਾਰਡ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physical Education Chapter 3 ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿੱਚ ਕਿੱਤੇ ਅਤੇ ਖੇਡ ਅਵਾਰਡ

Physical Education Guide for Class 12 PSEB ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿੱਚ ਕਿੱਤੇ ਅਤੇ ਖੇਡ ਅਵਾਰਡ Textbook Questions and Answers

ਇੱਕ ਅੰਕ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (One Mark Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਜਦੋਂ ਅੰਗਰੇਜ਼ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਭਾਰਤ ਆਏ ਤਾਂ ਉਹਨਾਂ ਨੇ ਆਪਣੇ ਬੱਚਿਆਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਲਈ ਕਿਹੋ ਜਿਹੇ ਸਕੂਲ ਖੋਲ੍ਹੇ ?
ਉੱਤਰ-
ਅੰਗਰੇਜ਼ ਖੇਡਾਂ ਦੇ ਬੜੇ ਸ਼ੌਕੀਨ ਸਨ ਅਤੇ ਉਹਨਾਂ ਨੇ ਹੀ ਪਹਿਲੀ ਵਾਰ ਕ੍ਰਿਕੇਟ, ਫੁੱਟਬਾਲ, ਜਿਮਨਾਸਟਿਕ, ਹਾਕੀ ਆਦਿ ਖੇਡਾਂ ਨੂੰ ਭਾਰਤ ਵਿਚ ਪੇਸ਼ ਕੀਤਾ ਅਤੇ ਆਪਣੇ ਬੱਚਿਆਂ ਨੂੰ ਪੜ੍ਹਾਉਣ ਵਾਸਤੇ ਅੰਗਰੇਜ਼ੀ ਸਕੂਲਾਂ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਬੀ. ਪੀ. ਐੱਡ ਦਾ ਕੋਰਸ ਕਿੰਨੇ ਸਾਲਾਂ ਦਾ ਹੈ ?
ਉੱਤਰ-
ਬੀ. ਪੀ. ਐੱਡ ਦਾ ਕੋਰਸ 2 ਸਾਲਾਂ ਦਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਰੀਰਿਕ ਸਿੱਖਿਆ ਦੀ ਭਾਰਤ ਵਿੱਚ ਹੋਂਦ ਕਦੋਂ ਹੋਈ ?
ਉੱਤਰ-
ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੀ ਹੋਂਦ 1920 ਤੋਂ ਮੰਨੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਐੱਨ.ਐੱਸ.ਐੱਨ. ਆਈ. ਐੱਸ. ਦਾ ਪੂਰਾ ਨਾਂ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨੇਤਾ ਜੀ ਸੁਭਾਸ਼ ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਨ ।

ਦੋ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Two Marks Question Answers)

ਪ੍ਰਸ਼ਨ 5.
ਅਰਜੁਨ ਅਵਾਰਡ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਕੀ ਯੋਗਤਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੇ ਲਗਾਤਾਰ ਚਾਰ ਸਾਲ ਤਕ ਕੌਮੀ ਅਤੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਪੱਧਰ ਜਿਵੇਂ ਕਿ ਓਲੰਪਿਕ ਖੇਡਾਂ, ਏਸ਼ੀਅਨ ਖੇਡਾਂ, ਕਾਮਨਵੈਲਥ ਅਤੇ ਰਾਸ਼ਟਰੀ ਪੱਧਰ ਤੇ ਬੇਹਤਰੀਨ ਪ੍ਰਦਰਸ਼ਨ ਕੀਤਾ ਹੋਵੇ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਰਟੀਫਿਕੇਟ ਕੋਰਸ ਇੰਨ ਯੋਗ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਇਹ ਕੋਰਸ ਬਾਰਵੀਂ ਤੋਂ ਬਾਅਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਜਿਸਦੀ ਮਿਆਦ 40 ਦਿਨਾਂ ਦੀ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਡਿਪਲੋਮਾ ਇੰਨ ਯੋਗ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਇਹ ਇਕ ਸਾਲ ਦੀ ਮਿਆਦ ਵਾਲਾ ਕੋਰਸ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਹ ਬੈਚਲਰ ਡਿਗਰੀ ਤੋਂ ਬਾਅਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ ਕਿਸ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਅਵਾਰਡ ਕੋਚਾਂ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਤਿੰਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Three Marks Question Answers)

ਪ੍ਰਸ਼ਨ 9.
ਖਿਡਾਰੀਆਂ ਲਈ ਫਿਜਿਉਥੈਰੇਪਿਸਟ ਦਾ ਕੀ ਰੋਲ ਹੈ ?
ਉੱਤਰ-
ਇਕ ਖੇਡ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਦੇ ਤੌਰ ਤੇ (As a Sports Physiotherapist) – ਜੇ ਵਿਅਕਤੀ ਨੂੰ ਖੇਡਾਂ ਵਿਚ ਲੱਗਣ ਵਾਲੀਆਂ ਸੱਟਾਂ ਅਤੇ ਪ੍ਰਬੰਧਨ ਦੀ ਜਾਣਕਾਰੀ ਹੋਏ ਤਾਂ ਉਹ ਇਸ ਕਿੱਤੇ ਨੂੰ ਖੇਡ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਦੇ ਤੌਰ ਤੇ ਅਪਣਾ ਸਕਦੇ ਹਨ । ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਬਣਨ ਦੀ ਯੋਗਤਾ ਡਿਪਲੋਮਾ, ਬੈਚਲਰ ਆਫ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਬੀ.ਐੱਸ.ਸੀ. (B.Sc.) ਇਨ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਜਾਂ ਮਾਸਿਕ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਲਾਜ਼ਮੀ ਹੈ । ਕੈਰੀਅਰ ਦੇ ਤੌਰ ‘ਤੇ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਲਈ ਸ਼ਾਨਦਾਰ ਮੌਕੇ ਹਨ । ਉਹ ਕਈ ਖੇਡ ਸੰਸਥਾਵਾਂ ਨਾਲ ਜੁੜ ਸਕਦੇ ਹਨ । ਰਾਸ਼ਟਰੀ ਟੀਮਾਂ ਜਾਂ ਫਿਰ ਨਿੱਜੀ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਦੇ ਤੌਰ ‘ਤੇ ਵੀ ਕੰਮ ਕਰ ਸਕਦੇ ਹਨ ਕਿਉਂਕਿ ਖੇਡ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਜਾਂ ਫਿਰ ਅਭਿਆਸ ਦੌਰਾਨ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸੱਟਾਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਲੱਗਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ ਅਤੇ ਇਹਨਾਂ ਦੇ ਇਲਾਜ ਵਾਸਤੇ ਭੌਤਿਕ-ਚਿਕਿਤਸਾ ਦੇ ਮਾਹਿਰਾਂ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਅਵਾਰਡ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਅਵਾਰਡ (Rajiv Gandhi Sports Award) – ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਅਵਾਰਡ ਸਾਬਕਾ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਰਾਜੀਵ ਗਾਂਧੀ ਦੀ ਯਾਦ ਵਿਚ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਹ ਸਭ ਤੋਂ ਵੱਡੇ ਰੈਂਕ ਦਾ ਰਾਸ਼ਟਰੀ ਅਵਾਰਡ ਹੈ ਅਤੇ ਇਹ ਖਿਡਾਰੀਆਂ ਦੇ ਮਨੋਬਲ ਅਤੇ ਵਿਸ਼ਵਾਸ ਨੂੰ ਉਤਸਾਹਿਤ ਕਰਨ ਲਈ ਇਹ 1991 ਵਿਚ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ । ਇਹ ਅਵਾਰਡ ਯੁਵਾ ਮਾਮਲਿਆਂ ਅਤੇ ਖੇਡ ਮੰਤਰਾਲੇ ਦੁਆਰਾ ਖਿਡਾਰੀਆਂ ਨੂੰ ਭਾਰਤ ਵਿਚ ਖੇਡਾਂ ਵਿਚ ਸ਼ਾਨਦਾਰ ਪ੍ਰਦਰਸ਼ਨ ਲਈ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਅਵਾਰਡ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੇ 7.5 ਲੱਖ ਦਾ ਨਕਦ ਇਨਾਮ ਅਤੇ ਤਮਗਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਇਹ ਅਵਾਰਡ ਵਿਸ਼ਵਨਾਥਨ ਆਨੰਦ (Vishwnathan Anand) ਨੇ 1992-1993 ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤਾ ਅਤੇ ਔਰਤਾਂ ਵਿਚ ਕਰਨਮ ਮਲੇਸ਼ਵਰੀ ਨੂੰ ਇਹ ਅਵਾਰਡ 1995-96 ਵਿਚ ਮਿਲਿਆ । ਪੰਕਜ ਅਡਵਾਨੀ ਇਕ ਅਜਿਹੇ ਪਹਿਲੇ ਖਿਡਾਰੀ ਹੋਏ ਹਨ ਜਿਨ੍ਹਾਂ ਨੂੰ ਦੋ ਖੇਡਾਂ ਸਨੂਕਰ (Snooker) ਅਤੇ ਬਿਲੀਅਰਡਜ਼ (Billiards) ਲਈ ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਅਵਾਰਡ ਮਿਲਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਅਵਾਰਡ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਅਵਾਰਡ ਪੰਜਾਬ ਸਰਕਾਰ ਦੁਆਰਾ ਸਿੱਖ ਰਾਜ ਦੇ ਆਗੂ ਦੇ ਨਾਂ ਤੇ 1978 ਵਿਚ ਸਥਾਪਿਤ ਕੀਤਾ ਸੀ । ਇਸ ਅਵਾਰਡ ਵਿਚ ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਦੀ ਫੀ ਤੇ 5 ਲੱਖ ਰੁਪਏ ਦੀ ਨਕਦ ਰਕਮ (2018 ਪਾਲਿਸੀ ਦੇ ਅਨੁਸਾਰ ਰਕਮ ਵਾਧਾ) ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । 2017 ਤੱਕ ਇਹ ਰਾਸ਼ੀ ਇੱਕ ਲੱਖ ਰੁਪਏ ਸੀ।
ਇਹ ਪੁਰਸਕਾਰ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਪੱਧਰ ਦੇ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਹਿੱਸਾ ਲਿਆ ਹੋਵੇ । ਸ: ਪਰਗਟ ਸਿੰਘ ਪਹਿਲੇ ਵਿਅਕਤੀ ਸਨ ਜਿਨ੍ਹਾਂ ਨੇ ਇਹ ਅਵਾਰਡ ਪ੍ਰਾਪਤ ਕੀਤਾ ।
ਇਹ ਅਵਾਰਡ 1996 ਤੋਂ 2005 ਤੱਕ ਮੁਅੱਤਲ ਕਰ ਦਿੱਤਾ ਗਿਆ ਸੀ ਅਤੇ 2006 ਵਿਚ ਇਸ ਨੂੰ ਦੁਬਾਰਾ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ ਸੀ ।

ਪੰਜ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Five Marks Question Answers)

ਪ੍ਰਸ਼ਨ 12.
ਖੇਡ ਸਿਖਲਾਈ ਕੀ ਹੈ ? ਇਸ ਦੀ ਸੰਖੇਪ ਰੂਪ ਵਿਚ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਖੇਡ ਸਿਖਲਾਈ ਖੇਡਾਂ ਵਿੱਚ ਆਮ ਵਰਤਿਆ ਜਾਣ ਵਾਲਾ ਸ਼ਬਦ ਹੈ ਪਰ ਵਿਸ਼ਾਲ ਤੌਰ ਤੇ : ਇਹ ਇਕ ਸੰਗਠਿਤ ਅਤੇ ਵਿਵਸਥਿਤ ਤੇ ਅਰਬਪੁਰਨ ਦੇ ਤੌਰ ਤੇ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਜਿਸ ਦਾ ਉਦੇਸ਼ ਵਿਅਕਤੀਗਤ, ਮਾਨਸਿਕ ਅਤੇ ਬੌਧਿਕ ਕਾਰਜਕੁਸ਼ਲਤਾ ਵਿਚ ਸੁਧਾਰ ਲਿਆਉਣਾ ਹੈ ।

ਖੇਡ ਸਿਖਲਾਈ ਲਈ ਹੇਠ ਲਿਖੇ ਕੋਰਸ ਕਰਵਾਏ ਜਾਂਦੇ ਹਨ :-
ਮਾਸਟਰ ਡਿਗਰੀ ਇਨ ਸਪੋਰਟਸ ਕੋਚਿੰਗ (Master degree in Sports Coaching) – ਇਹ ਦੋ ਸਾਲ ਦੀ ਮਿਆਦ ਵਾਲੀ ਡਿਗਰੀ ਹੈ ਜਿਸ ਵਿਚ ਕੋਚਾਂ ਵਿਚ ਰਿਸਰਚ ਵਿਵਹਾਰ ਦਾ ਵਿਕਾਸ ਕਰਨਾ ਹੈ । ਇਹ ਡਿਗਰੀ ਐਥਲੈਟਿਕਸ, ਬਾਸਕੇਟਬਾਲ, ਫੁੱਟਬਾਲ, ਹਾਕੀ, ਸਵੀਮਿੰਗ, ਵਾਲੀਬਾਲ, ਵੇਟ ਲਿਫਟਿੰਗ ਅਤੇ ਕੁਸ਼ਤੀ ਲਈ ਮੌਜ਼ੂਦ ਹੈ ਅਤੇ ਪੰਜਾਬੀ ਯੂਨੀਵਰਸਿਟੀ ਪਟਿਆਲਾ ਨਾਲ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੈ । ਇਸ ਡਿਗਰੀ ਵਾਸਤੇ ਵਿਅਕਤੀ ਗੈਜੁਏਟ ਅਤੇ ਐੱਸ.ਏ.ਆਈ (SAI) ਜਾਂ ਐੱਨ.ਐੱਸ.ਐੱਨ. ਆਈ. ਐੱਸ (NSNIS) ਤੋਂ 60% ਨਾਲ ਡਿਪਲੋਮਾ ਪਾਸ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਸਰਟੀਫਿਕੇਟ ਕੋਰਸ ਇਨ ਸਪੋਰਟਸ ਕੋਚਿੰਗ (Certificate Course in Sports Coaching) – ਇਹ ਛੇ ਹਫਤਿਆਂ ਦਾ ਸਰਟੀਫਿਕੇਟ ਕੋਰਸ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸ ਵਿਚ ਸਕੂਲ, ਕਾਲਜਾਂ, ਯੂਨੀਵਰਸਿਟੀ, ਜਾਂ ਕਿਸੇ ਵੀ ਸਪੋਰਟਸ ਏਜੰਸੀ ਦੇ ਅਧਿਆਪਕ ਜਾਂ ਕੋਚ ਇਸ ਨੂੰ ਕਰ ਸਕਦੇ ਹਨ ।

ਡਿਪਲੋਮਾ ਇਨ ਸਪੋਰਟਸ ਕੋਚਿੰਗ (Diploma in Sports Coaching) – ਇਹ ਇਕ ਸਾਲ ਦਾ ਹੁੰਦਾ ਹੈ ਜਿਸ ਵਿਚ ਕੋਚ ਬਣਨ ਆਏ ਵਿਅਕਤੀ ਆਪਣੀ-ਆਪਣੀ ਖੇਡ ਵਿਚ ਮੁਹਾਰਤ ਹਾਸਿਲ ਕਰਦੇ ਹਨ । ਇਹ 12ਵੀਂ ਤੋਂ ਬਾਅਦ ਕਿਸੇ ਵੀ ਉੱਚ ਡਿਗਰੀ ਤੋਂ ਬਾਅਦ ਵਿਚ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਵਿਅਕਤੀ ਨੇ ਆਪਣੀ-ਆਪਣੀ ਖੇਡ ਵਿਚ ਉਪਲੱਬਧੀ ਹਾਸਿਲ ਕੀਤੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਸਰੀਰਿਕ ਸਿੱਖਿਆ ਵਿੱਚ ਕਿੱਤੇ ਅਤੇ ਖੇਡ ਅਵਾਰਡ ਦੀ ਕੀ ਮਹੱਤਤਾ ਹੈ ? ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੀ ਭਾਰਤ ਵਿੱਚ ਹੋਂਦ ਬਾਰੇ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਰੀਰਕ ਸਿੱਖਿਆ ਇਕ ਅਜਿਹੀ ਸਿੱਖਿਆ ਹੈ ਜੋ ਕਿ ਸਰੀਰਕ ਗਤੀਵਿਧੀਆਂ, ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ, ਜੀਵਨ ਸ਼ੈਲੀ, ਖੇਡਾਂ ਅਤੇ ਅੰਤਰ-ਨਿਜੀ ਹੁਨਰ ਦੇ ਰਾਹੀਂ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਵਿਚ ਕੈਰੀਅਰ ਦੇ ਮੌਕੇ ਦਿਨੋਦਿਨ ਭਾਰਤ ਅਤੇ ਵਿਦੇਸ਼ਾਂ ਵਿਚ ਵੱਧ ਰਹੇ ਹਨ | ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਵਿਸ਼ੇ ਵਿਚ ਕੈਰੀਅਰ ਬਣਾਉਣ ਦਾ ਵਿਕਲਪ ਆਸਾਨ ਨਹੀਂ ਹੈ । ਇਸ ਵਿਚ ਭਾਰਤ ਦੀਆਂ ਕਈ ਸਰਕਾਰੀ ਸੰਸਥਾਵਾਂ ਜਿਵੇਂ ਸਪਰੋਟਸ ਅਥਾਰਿਟੀ ਆਫ ਇੰਡੀਆ, ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਵਾਂ, ਵੱਖ-ਵੱਖ ਯੂਥ ਸੇਵਾਵਾਂ ਅਤੇ ਖੇਡ ਵਿਭਾਗ, ਰੇਲਵੇਜ਼, ਬੈਂਕ, ਭਾਰਤੀ ਏਅਰਲਾਈਨਜ਼, ਸੂਬਾ ਪੁਲਿਸ ਵਰਗੀਆਂ ਸੰਸਥਾਵਾਂ ਬਹੁਤ ਸਾਰੀਆਂ ਨੌਕਰੀਆਂ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ । ਇਹ ਨੌਕਰੀਆਂ ਖੇਡ ਕੋਟੇ ਦੇ ਅਧੀਨ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਅੱਜ ਦੇ ਦੌਰ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਨੌਕਰੀਆਂ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਖੇਤਰ ਮੌਕੇ ਪ੍ਰਦਾਨ ਕਰ ਰਹੇ ਹਨ ।

ਇਹ ਖੇਡ ਅਵਾਰਡ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਖੇਡਾਂ ਲਈ ਦਿੱਤੇ ਗਏ ਹਨ । ਖਿਡਾਰੀ ਅਤੇ ਕੋਚ ਦੇ ਖੇਡਾਂ ਵਿਚ ਯੋਗਦਾਨ ਲਈ ਅਤੇ ਉਹਨਾਂ ਦੇ ਮਨੋਬਲ ਨੂੰ ਉੱਚਾ ਚੁੱਕਣ ਲਈ ਖੇਡ ਅਵਾਰਡਾਂ ਨੂੰ ਹਰ ਸਾਲ ਸਾਡੇ ਦੇਸ਼ ਦੇ ਮਹਾਨ ਹਾਕੀ ਖਿਡਾਰੀ ਮੇਜਰ ਧਿਆਨਚੰਦ ਦੇ ਜਨਮ ਦਿਹਾੜੇ, 29 ਅਗਸਤ ਨੂੰ ਹਰ ਸਾਲ ਰਾਸ਼ਟਰਪਤੀ ਭਵਨ ਵਿਚ ਰਾਸ਼ਟਰਪਤੀ ਦੁਆਰਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ 29 ਅਗਸਤ ਨੂੰ ਦੇਸ਼ ਦੇ ਰਾਸ਼ਟਰੀ ਖੇਡ ਦਿਵਸ (National Sports Day) ਦੇ ਰੂਪ ਵਿੱਚ ਵੀ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਜੋ ਖਿਡਾਰੀਆਂ ਅਤੇ ਭਵਿੱਖ ਵਿਚ ਉਭਰਦੇ ਖਿਡਾਰੀ ਨੂੰ ਪ੍ਰੇਰਨਾ ਮਿਲ ਸਕੇ ।

ਖੇਡਾਂ ਮਨੁੱਖੀ ਸੱਭਿਅਤਾ ਦਾ ਹਮੇਸ਼ਾ ਸਰਗਰਮ ਹਿੱਸਾ ਰਹੀਆਂ ਹਨ | ਜੇਕਰ ਅਸੀਂ ਆਪਣੀ ਪੁਰਾਣੀ ਸੱਭਿਅਤਾ ਤੇ ਨਜ਼ਰ ਮਾਰੀਏ ਤਾਂ ਵੈਦਿਕ ਸਮਾਂ (Vedic period), ਮਹਾਂਕਾਵਿ (Epic period) ਅਤੇ ਇਤਿਹਾਸਿਕ ਦੌਰ (Historical period) ਵਿਚ ਖੇਡਾਂ ਦੀ ਆਪਣੀ ਮਹੱਤਵਪੂਰਨ ਜਗਾ ਸੀ । ਕਈ ਖੋਜਾਂ ਤੋਂ ਪਤਾ ਲੱਗਿਆ ਹੈ ਕਿ ਲੋਕ ਖੇਡ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਹਿੱਸਾ ਲੈਂਦੇ ਸਨ । ਇਹ ਤੀਰ ਅੰਦਾਜ਼ੀ, ਘੋੜੇ ਦੀ ਸਵਾਰੀ, ਹਥਿਆਰ ਸਿਖਲਾਈ, ਸ਼ਿਕਾਰ, ਤਲਵਾਰਬਾਜ਼ੀ, ਤੈਰਾਕੀ ਅਤੇ ਗੱਦਾ (Gada) ਲੜਾਈ ਵਰਗੀਆਂ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਭਾਗ ਲੈਂਦੇ ਸਨ । ਹਾਲਾਂਕਿ ਬ੍ਰਿਟਿਸ਼ ਲੋਕ ਵੀ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਚਾਹਵਾਨ ਸਨ ਉਹਨਾਂ ਨੇ ਭਾਰਤ ਵਿਚ ਸਰੀਰਕ ਸੱਭਿਆਚਾਰ ਨੂੰ ਵਿਕਸਿਤ ਕੀਤਾ । 1858 ਵਿਚ ਈਸਟ ਇੰਡੀਆ ਕੰਪਨੀ ਭਾਰਤ ਵਿਚ ਦਾਖ਼ਲ ਹੋਈ ਅਤੇ ਸਾਰਾ ਭਾਰਤ ਟਿਸ਼ ਸ਼ਾਸਨ ਦੇ ਅਧੀਨ ਆ ਗਿਆ | ਅੰਗਰੇਜ਼ ਖੇਡਾਂ ਦੇ ਬੜੇ ਸ਼ੌਕੀਨ ਸਨ ਅਤੇ ਉਹਨਾਂ ਨੇ ਹੀ ਪਹਿਲੀ ਵਾਰ ਕਿਕੇਟ, ਫੁੱਟਬਾਲ, ਜਿਮਨਾਸਟਿਕ, ਹਾਕੀ ਆਦਿ ਖੇਡਾਂ ਨੂੰ ਭਾਰਤ ਵਿਚ ਪੇਸ਼ ਕੀਤਾ ਅਤੇ ਆਪਣੇ ਬੱਚਿਆਂ ਨੂੰ ਪੜ੍ਹਾਉਣ ਵਾਸਤੇ ਅੰਗਰੇਜ਼ੀ ਸਕੂਲਾਂ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ।

ਪ੍ਰਸ਼ਨ 14.
ਹੇਠ ਦਰਸਾਏ ਕੋਰਸਾਂ ਲਈ ਕੀ ਯੋਗਤਾ ਚਾਹੀਦੀ ਹੈ ? ਇਹ ਕੋਰਸ ਕਰਨ ਦਾ ਸਮਾਂ ਵੀ ਦੱਸੋ ।
(ਉ) ਬੀ. ਪੀ. ਐੱਡ.
(ਅ) ਡੀ. ਪੀ. ਐੱਡ.
(ਈ ਸਰਟੀਫਿਕੇਟ ਕੋਰਸ ਇੰਨ ਯੋਗ
(ਸ) ਪੀ. ਐੱਚ. ਡੀ. ।
ਉੱਤਰ-
(ੳ) ਬੀ.ਪੀ.ਐੱਡ. (ਇੰਟੀਗਰੇਟਿਡ ਕੋਰਸ) – ਇਹ ਕੋਰਸ ਚਾਰ ਸਾਲ ਦੀ ਮਿਆਦ ਵਾਲਾ ਹੈ ਅਤੇ ਕਈ ਕਾਲਜਾਂ ਅਤੇ ਯੂਨੀਵਰਸਿਟੀ ਵਲੋਂ ਕਰਵਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਵੀ ਬੈਚਲਰ ਆਫ ਆਰਟਸ ਦੇ ਬਰਾਬਰ ਦੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਡਿਗਰੀ ਹੁੰਦੀ ਹੈ । ਪਹਿਲਾਂ ਇਸ ਕੋਰਸ ਦੀ ਮਿਆਦ ਤਿੰਨ ਸਾਲ ਦੀ ਰੱਖੀ ਗਈ ਪਰ ਐੱਨ.ਸੀ.ਆਰ.ਟੀ. ਨੇ 2016-17 ਵਿਚ ਇਸ ਦੀ ਮਿਆਦ ਬਦਲ ਕੇ ਚਾਰ ਸਾਲ ਕਰ ਦਿੱਤੀ ਗਈ ਹੈ । ਚਾਰ ਸਾਲ ਪੂਰੇ ਹੋਣ ਤੋਂ ਬਾਅਦ ਵਿਅਕਤੀ ਸਿੱਧੇ ਤੌਰ ‘ਤੇ ਐੱਮ.ਪੀ.ਐੱਡ. ਵਿਚ ਦਾਖਲਾ ਲੈ ਸਕਦਾ ਹੈ । ਬੀ.ਪੀ. ਐੱਡ. ਦੀ ਡਿਗਰੀ ਪੂਰੀ ਕਰਨ ਤੋਂ ਬਾਅਦ ਵਿਅਕਤੀ ਕਿਸੇ ਵੀ ਸਕੂਲ ਵਿਚ ਪੀ.ਟੀ.ਆਈ. ਕੰਮ ਕਰ ਸਕਦਾ ਹੈ ।

ਬੀ. ਪੀ. ਐੱਡ. ਲਈ ਯੋਗਤਾ
(ਉ) ਕਿਸੇ ਵੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਬੋਰਡ ਤੋਂ ਬਾਰਵੀਂ 50% ਅੰਕਾਂ ਨਾਲ ਪਾਸ ਕੀਤੀ ਹੋਵੇ ।
(ਅ) ਦਾਖ਼ਲੇ ਵਾਸਤੇ ਇਨਟਰੈਨਸ ਪੇਪਰ ਅਤੇ ਫਿਜ਼ੀਕਲ ਟੈਸਟ ਪਾਸ ਕੀਤਾ ਹੋਵੇ । (ੲ) ਵਿਅਕਤੀ ਕਿਸੇ ਖੇਡ ਵਿਚ ਮਾਹਿਰ ਜ਼ਰੂਰ ਹੋਵੇ ।
(ਸ) ਡੀ.ਪੀ. ਐੱਡ. ਡਿਗਰੀ 50% ਅੰਕਾਂ ਨਾਲ ਪਾਸ ਹੋਵੇ ।
(ਅ) ਡੀ. ਪੀ. ਐੱਡ.- ਇਹ ਕੋਰਸ ਪਹਿਲਾਂ ਸੀ.ਪੀ. ਐੱਡ ਦੇ ਨਾਮ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਸੀ ਅਤੇ ਬਾਅਦ ਵਿਚ ਇਸ ਨੂੰ ਡੀ.ਪੀ.ਐੱਡ ਕਿਹਾ ਜਾਣ ਲੱਗ ਪਿਆ । ਇਸਦੇ ਨਾਲ ਹੀ ਇਸ ਦੀ ਮਿਆਦ ਇਕ ਸਾਲ ਤੋਂ ਵਧਾ ਕੇ ਦੋ ਸਾਲ ਕਰ ਦਿੱਤੀ ਗਈ ਸੀ । ਇਸ ਕੋਰਸ ਨੂੰ ਪੂਰਾ ਕਰਕੇ ਵਿਅਕਤੀ ਕਿਸੇ ਵੀ ਐਲੀਮੈਂਟਰੀ ਸਕੂਲ ਪੀ.ਟੀ.ਆਈ. ਦੇ ਤੌਰ ‘ਤੇ ਅਧਿਆਪਕ ਵਜੋਂ ਕੰਮ ਕਰ ਸਕਦਾ ਹੈ ।

ਡੀ. ਪੀ. ਐੱਡ. ਵਿਚ ਦਾਖ਼ਲੇ ਲਈ ਯੋਗਤਾ-
(ਉ) ਵਿਅਕਤੀ ਨੇ ਕਿਸੇ ਵੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਬੋਰਡ ਤੋਂ ਬਾਰ੍ਹਵੀਂ 50% ਅੰਕਾਂ ਨਾਲ ਪਾਸ ਕੀਤੀ ਹੋਵੇ ।
(ਅ) ਉਹ ਫਿਜੀਕਲ ਤੌਰ ‘ਤੇ ਤੰਦਰੁਸਤ ਹੋਵੇ ।
(ਈ) ਉਸ ਨੇ ਦਾਖ਼ਲੇ ਵਾਸਤੇ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਦਾ ਟੈਸਟ ਪਾਸ ਕੀਤਾ ਹੋਵੇ ।
(ਬ ਸਰਟੀਫਿਕੇਟ ਇੰਨ ਯੋਗਾ-ਇਸ ਕੋਰਸ ਨੂੰ ਕਰਨ ਵਾਸਤੇ ਘੱਟੋ-ਘੱਟ ਬਾਰਵੀਂ ਪਾਸ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਇਹ ਛੇ ਹਫ਼ਤਿਆਂ ਦੀ ਮਿਆਦ ਵਾਲਾ ਕੋਰਸ ਹੁੰਦਾ ਹੈ ਜਿਸ ਵਿਚ ਯੋਗਾ ਦੇ ਆਸਨਾਂ ਦਾ ਗਿਆਨ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
(ਸ) ਪੀ. ਐੱਚ. ਡੀ. (ਡਾਕਟਰ ਆਵ ਫਿਲਾਸਫੀ)-ਇਹ ਸਭ ਤੋਂ ਉੱਚੀ ਡਿਗਰੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਦੀ ਮਿਆਦ 3 ਸਾਲ ਤੋਂ 4 ਸਾਲ ਤੱਕ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਵਿਅਕਤੀ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਕਿਸੇ ਵੀ ਵਿਸ਼ੇ ਤੇ ਆਪਣੀ ਰੁਚੀ ਮੁਤਾਬਿਕ ਨਵੀਂ ਖੋਜ ਕਰਦਾ ਹੈ ਅਤੇ ਜੋ ਨਤੀਜੇ ਆਉਂਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਵਿਕਾਸ ਵਿਚ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਡਿਗਰੀ ਨੂੰ ਪੂਰਾ ਕਰਨ ਤੋਂ ਵਿਅਕਤੀ ਨੂੰ ਡਾਕਟਰ ਦੀ ਉਪਾਧੀ ਨਾਲ ਨਿਵਾਜਿਆ ਜਾਂਦਾ ਹੈ ।
ਯੋਗਤਾ-

1. ਇਸ ਵਿਚ ਪ੍ਰਵੇਸ਼ ਪ੍ਰੀਖਿਆ ਪਾਸ ਕਰਨੀ ਜ਼ਰੂਰੀ ਹੁੰਦੀ ਹੈ ਜੇਕਰ ਵਿਅਕਤੀ ਨੇ ਯੂ.ਜੀ.ਸੀ. ਨੈੱਟ ਨਹੀਂ ਪਾਸ ਕੀਤਾ ।
2. ਐੱਮ.ਪੀ.ਐੱਡ. ਮਾਸਟਰ ਡਿਗਰੀ ਅਤੇ ਐੱਮ. ਫਿਲ. ਤੋਂ ਬਾਅਦ ਇਸ ਨੂੰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

PSEB 12th Class Physical Education Guide ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿੱਚ ਕਿੱਤੇ ਅਤੇ ਖੇਡ ਅਵਾਰਡ Important Questions and Answers

ਇੱਕ ਅੰਕ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (One Mark Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਵਾਈ. ਐੱਮ. ਸੀ. ਏ. (YMCA) ਕਾਲਜ ਨੂੰ ਕਿਸ ਸਾਲ ਵਿਚ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
1920.

ਪ੍ਰਸ਼ਨ 2.
ਇੰਡੀਅਨ ਉਲੰਪਿਕ ਕਿਸ ਸਾਲ ਬਣਾਈ ਗਈ ਸੀ ?
ਉੱਤਰ-
1927 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 3.
ਭਾਰਤੀ ਐਜੂਕੇਸ਼ਨ ਕਮਿਸ਼ਨ ਦਾ ਦੂਜਾ ਨਾਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਕੋਠਾਰੀ ਕਮਿਸ਼ਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਮਦਰਾਸ ਵਿਚ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਯੋਗਦਾਨ ਵਿਚ ਪ੍ਰਮੁੱਖ ਸੰਸਥਾ ਦਾ ਨਾਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਵਾਈ. ਐਮ. ਸੀ. ਏ. ।

ਪ੍ਰਸ਼ਨ 5.
ਸਕੂਲੀ ਪੱਧਰ ਤੇ, ਅਧਿਆਪਕ ਦੀ ਕੀ ਯੋਗਤਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਡੀ.ਪੀ. ਐੱਡ., ਬੀ.ਪੀ. ਐੱਡ. ਅਤੇ ਐੱਮ.ਪੀ. ਐੱਡ. ।

ਪਸ਼ਨ 6.
ਖੇਡਾਂ ਵਿਚ ਕੋਚਿੰਗ ਪੇਸ਼ੇ ਲਈ ਕੀ ਯੋਗਤਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਐਨ. ਐੱਸ. ਐਨ. ਆਈ. ਐੱਸ. (NSNIS) ।

ਪ੍ਰਸ਼ਨ 7.
ਕਾਲਜ ਅਧਿਆਪਕਾਂ ਦੀ ਕੀ ਯੋਗਤਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਐੱਮ.ਪੀ. ਐੱਡ., ਯੂ. ਜੀ. ਸੀ. (ਨੈੱਟ) ਅਤੇ ਪੀ-ਐੱਚ. ਡੀ. ।

ਪ੍ਰਸ਼ਨ 8.
ਕਿਸ ਸਾਲ ਵਿਚ ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਅਵਾਰਡ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
1991 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 9.
ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਅਵਾਰਡ ਵਿਚ ਦਿੱਤੀ ਜਾਣ ਵਾਲੀ ਨਕਦ ਰਾਸ਼ੀ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
7.5 ਲੱਖ ਰੁਪਏ ।

ਪ੍ਰਸ਼ਨ 10.
ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਅਵਾਰਡ ਕਿਸ ਮਹਿਲਾ ਨੂੰ ਮਿਲਿਆ ਸੀ ?
ਉੱਤਰ-
ਕਰਨਮ ਮਲੇਸ਼ਵਰੀ ਨੂੰ ਭਾਰ ਤੋਲਨ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 11.
ਨਾਭਾ ਦਾ (NADA) ਦਾ ਪੂਰਾ ਨਾਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਨੈਸ਼ਨਲ ਐਂਟੀ ਡੋਪਿੰਗ ਏਜੰਸੀ ।

ਪ੍ਰਸ਼ਨ 12.
ਵਾਲਾ (WADA) ਦਾ ਪੂਰਾ ਨਾਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵੱਲਡ ਐਂਟੀ ਡੋਪਿੰਗ ਏਜੰਸੀ ।

ਪ੍ਰਸ਼ਨ 13.
ਸਾਲ 2018 ਵਿਚ, ਐਥਲੈਟਿਕਸ ਵਿਚ ਅਰਜੁਨ ਅਵਾਰਡ ਪੁਰਸਕਾਰ ਕਿਸ ਨੇ ਪ੍ਰਾਪਤ ਕੀਤਾ ਸੀ ?
ਉੱਤਰ-
ਨੀਰਜ ਚੋਪੜਾ, ਸੂਬੇਦਾਰ ਜਿਨਸਨ ਜੋਨਸਨ ਅਤੇ ਹਿਮਾ ਦਾਸ ।

ਪ੍ਰਸ਼ਨ 14.
ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਮਾਸਟਰ ਡਿਗਰੀ ਦੀ ਮਿਆਦ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਦੋ ਸਾਲ ।

ਪ੍ਰਸ਼ਨ 15.
ਕੋਚਾਂ ਦੇ ਯੋਗਦਾਨ ਲਈ ਕਿਹੜਾ ਪੁਰਸਕਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ ।

ਪ੍ਰਸ਼ਨ 16.
ਸਪੋਰਟਸ ਅਥਾਰਿਟੀ ਆਂਫ ਇੰਡੀਆ ਦਾ ਨਵਾਂ ਨਾਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸਪੋਰਟਸ ਇੰਡੀਆ ।

ਪ੍ਰਸ਼ਨ 17.
ਕਿਸ ਸਾਲ ਵਿਚ ‘‘ਅਥਾਰਿਟੀ’ ਸ਼ਬਦ ਨੂੰ ਸਪੋਟਰਸ ਅਥਾਰਿਟੀ ਆਫ ਇੰਡੀਆ ਵਿਚੋਂ ਹਟਾ ਦਿੱਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
2018 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 18.
ਭਾਰਤ ਵਿਚ ਖਿਡਾਰੀ ਨੂੰ ਦਿੱਤੇ ਜਾਣ ਵਾਲੇ ਖੇਡ ਅਵਾਰਡ ਦਾ ਕੀ ਨਾਮ ਹੈ ?
ਉੱਤਰ-
ਅਰਜੁਨ ਅਵਾਰਡ ।

ਪ੍ਰਸ਼ਨ 19.
ਭਾਰਤ ਵਿਚ ਕੋਚਾਂ ਨੂੰ ਦਿੱਤਾ ਜਾਣ ਵਾਲਾ ਸਰਵੋਤਮ ਅਵਾਰਡ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ-
ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ ।

ਪ੍ਰਸ਼ਨ 20.
ਸੰਨ 1961 ਵਿਚ, ਅਰਜੁਨ ਅਵਾਰਡ ਐਥਲੈਟਿਕਸ ਵਿਚ ਕਿਸ ਨੂੰ ਮਿਲਿਆ ਸੀ ?
ਉੱਤਰ-
ਗੁਰਬਚਨ ਸਿੰਘ ਰੰਧਾਵਾ ।

ਪ੍ਰਸ਼ਨ 21.
ਆਈ. ਓ. ਏ. (IOA) ਦੀ ਸਥਾਪਨਾ ਕਿਸ ਸਾਲ ਹੋਈ ?
ਉੱਤਰ-
1927 ਵਿੱਚ ।

ਪ੍ਰਸ਼ਨ 22.
1968 ਵਿਚ, ਖੇਡ ਨੀਤੀ ਦੀ ਘੋਸ਼ਣਾ ਕਿਸ ਨੇ ਕੀਤੀ ਸੀ ?
ਉੱਤਰ-
ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਇੰਦਰਾ ਗਾਂਧੀ ਨੇ ।

ਪ੍ਰਸ਼ਨ 23.
ਸਪੋਰਟਸ ਅਥਾਰਿਟੀ ਆਫ਼ ਇੰਡੀਆ ਦਾ ਉਦੇਸ਼ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਖੇਡਾਂ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਸਹੂਲਤਾਂ ਨੂੰ ਉੱਚਿਤ ਵਰਤੋਂ ਵਿਚ ਲਿਆਉਣਾ ਅਤੇ ਖੇਡਾਂ ਦੀ ਉੱਨਤੀ ਅਤੇ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਚਲਾਉਣਾ ।

ਪ੍ਰਸ਼ਨ 24.
ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਬਾਰਵੀਂ ਤੋਂ ਬਾਅਦ ਬੈਚਲਰ ਡਿਗਰੀ ਦੀ ਮਿਆਦ ਤਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
4 ਸਾਲ ।

ਪ੍ਰਸ਼ਨ 25.
ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਡੀ. ਪੀ. ਐੱਡ. ਕਿੰਨੇ ਸਾਲ ਦੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
2 ਸਾਲ ।

ਪ੍ਰਸ਼ਨ 26.
ਖੇਡ ਪੁਰਸਕਾਰ ਹਰ ਸਾਲ ਕਿਸ ਤਰੀਖ ਤੇ ਵੰਡੇ ਜਾਂਦੇ ਹਨ ਅਤੇ ਕਿੱਥੇ ? .
ਉੱਤਰ-
ਖੇਡ ਪੁਰਸਕਾਰ ਹਰ 29 ਅਗਸਤ ਨੂੰ ਰਾਸ਼ਟਰਪਤੀ ਭਵਨ ਵਿਚ ਵੰਡੇ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 27.
ਰਾਸ਼ਟਰੀ ਖੇਡ ਦਿਵਸ ਕਿਸ ਮਹਾਨ ਖਿਡਾਰੀ ਦੇ ਜਨਮ ਦਿਨ ਦੇ ਰੂਪ ਵਿਚ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਮੇਜਰ ਧਿਆਨ ਚੰਦ ਜੀ ।

ਪ੍ਰਸ਼ਨ 28.
ਵਿਰਾਟ ਕੋਹਲੀ ਨੂੰ ਕਿਸ ਸਾਲ ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਪੁਰਸਕਾਰ ਮਿਲਿਆ ਸੀ ?
ਉੱਤਰ-
ਸਾਲ 2018 ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 29.
ਪੰਜਾਬ ਰਾਜ ਦਾ ਸਭ ਤੋਂ ਵੱਡਾ ਖੇਡ ਅਵਾਰਡ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ-
ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਅਵਾਰਡ ।

ਪ੍ਰਸ਼ਨ 30.
ਮੌਲਾਨਾ ਅਬੁਲ ਕਲਾਮ ਅਜ਼ਾਦ ਅਵਾਰਡ ਕਿਸ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਖੇਡ ਵਿਚ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨ ਵਾਲੀ ਸਰਵੋਤਮ ਯੂਨੀਵਰਸਿਟੀ ਨੂੰ ।

ਪ੍ਰਸ਼ਨ 31.
ਮੌਲਾਨਾ ਅਬੁਲ ਕਲਾਮ ਅਜ਼ਾਦ ਅਵਾਰਡ ਦੀ ਇਨਾਮੀ ਰਕਮ ਕਿੰਨੀ ਹੈ ?
ਉੱਤਰ-
10 ਲੱਖ ਰੁਪਏ ।

ਪ੍ਰਸ਼ਨ 32.
ਮਾਕਾ (Maka) ਦਾ ਪੂਰਾ ਨਾਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਮੌਲਾਨਾ ਅਬੁਲ ਕਲਾਮ ਅਜ਼ਾਦ ।

ਪ੍ਰਸ਼ਨ 33.
ਸਾਈ (SAI) ਦੇ ਨਾਮ ਵਿਚ ਕੀ ਬਦਲਿਆ ਗਿਆ ਹੈ ?
ਉੱਤਰ-
ਸਪੋਰਟਸ ਇੰਡੀਆ ।

ਦੋ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Two Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਵੱਖ-ਵੱਖ ਕੈਰੀਅਰ ਵਿਕਲਪਾਂ ਦੀ ਸੂਚੀ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਸਿੱਖਿਆਰਥੀ ਦੇ ਰੂਪ ਵਿਚ
2. ਫਿਟਨੈੱਸ ਟ੍ਰੇਨਰ ਦੇ ਰੂਪ ਵਿਚ
3. ਕੋਚਿੰਗ ਕਿੱਤੇ ਦੇ ਰੂਪ ਵਿਚ ।
4. ਖੇਡ ਪੱਤਰਕਾਰ ਦੇ ਰੂਪ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 2.
LNIPE ਤੇ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਾਲ 1957 ਵਿਚ, ਲਕਸ਼ਮੀ ਬਾਈ ਨੈਸ਼ਨਲ ਕਾਲਜ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ਗਈ ਸੀ । ਇਹ ਗਵਾਲੀਅਰ ਵਿਖੇ ਸਥਿਤ ਹੈ ਅਤੇ ਇਹ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਅਧਿਆਪਕਾਂ ਅਤੇ ਸਰੀਰਕ ਸਿੱਖਿਆ ਨੂੰ ਦੇਸ਼ ਵਿਚ ਬੜਾਵਾ ਦੇ ਰਿਹਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਕੋਚਾਂ ਵਾਸਤੇ ਕੀ ਯੋਗਤਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਐਨ.ਆਈ.ਐਸ. ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਕੋਚਿੰਗ ਡਿਪਲੋਮੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਰਾਜ ਕੁਮਾਰੀ ਅੰਮ੍ਰਿਤ ਕੌਰ ਕੋਚਿੰਗ ਸਕੀਮ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਰਾਜ ਕੁਮਾਰੀ ਅੰਮ੍ਰਿਤ ਕੌਰ ਕੋਚਿੰਗ ਸਕੀਮ 1953 ਵਿਚ ਸ਼ੁਰੂ ਕੀਤੀ ਗਈ ਸੀ । ਅੱਠ ਸਾਲਾਂ ਦੇ ਬਾਅਦ ਇਸ ਨੂੰ ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਨ ਵਿਚ ਮਿਲਾ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਸਕੀਮ ਦਾ ਉਦੇਸ਼ ਖਿਡਾਰੀਆਂ ਨੂੰ ਸਿਖਲਾਈ ਪ੍ਰਦਾਨ ਕਰਨਾ ਸੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਖੇਡਾਂ ਵਿਚ ਖੇਡ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਦੀ ਭੂਮਿਕਾ ਹੈ ।
ਉੱਤਰ-
ਜੋ ਵਿਅਕਤੀ ਖੇਡਾਂ ਵਿਚ ਲੱਗਣ ਵਾਲੀਆਂ ਸੱਟਾਂ ਅਤੇ ਪ੍ਰਬੰਧਨ ਦੀ ਜਾਣਕਾਰੀ ਹੋਏ ਉਹ ਇਸ ਕਿੱਤੇ ਨੂੰ ਖੇਡ ਫਿਜਿਉਥੈਰੇਪਿਸਟ ਦੇ ਤੌਰ ਤੇ ਅਪਣਾ ਸਕਦੇ ਹਨ । ਫਿਜਿਉਥੈਰੇਪਿਸਟ ਬਣਨ ਦੀ ਯੋਗਤਾ ਡਿਪਲੋਮਾ, ਬੈਚਲਰ ਆਫ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਬੀ.ਐਸ. (B.Sc.) ਇਨ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਜਾਂ ਮਾਸਿਕ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਲਾਜ਼ਮੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਪੋਰਟਸ ਅਵਾਰਡ ਬਾਰੇ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਉ ।
ਉੱਤਰ-
ਅਰਜੁਨ ਅਵਾਰਡ, ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ, ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਅਵਾਰਡ, ਧਿਆਨਚੰਦ ਅਵਾਰਡ, ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਅਵਾਰਡ ਅਤੇ ਮਾਕਾ ।

ਪ੍ਰਸ਼ਨ 7.
ਅਰਜੁਨ ਅਵਾਰਡ ਲਈ ਕੋਈ ਦੋ ਨਿਯਮਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਅਰਜੁਨ ਪੁਰਸਕਾਰ ਦਾ ਉਦੇਸ਼ ਭਾਰਤ ਵਿਚ ਖੇਡਾਂ ਦੇ ਵਿਕਸਿਤ ਮਿਆਰਾਂ ਨੂੰ ਵਿਕਸਿਤ ਕਰਨਾ ਹੈ ਅਤੇ ਭਾਰਤ ਸਰਕਾਰ ਹਰ ਸਾਲ ਮਿੱਥੇ ਸਮੇਂ ਤੇ ਖਿਡਾਰੀਆਂ ਦੇ ਨਾਮ ਸੂਚੀ ਫੈਡਰੇਸ਼ਨ ਤੋਂ ਮੰਗ ਲੈਂਦੀ ਹੈ ।
2. ਇਹ ਅਵਾਰਡ ਮਰਨ ਤੋਂ ਬਾਅਦ ਵੀ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
IOA ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ-
ਭਾਰਤੀ ਓਲੰਪਿਕ ਐਸੋਸੀਏਸ਼ਨ ਨੂੰ ਭਾਰਤੀ ਓਲੰਪਿਕ ਸੰਘ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਹ 1927 ਵਿਚ ਡਾ: ਏ.ਜੀ. ਨੋਇਟਰੇਨ (A.G. Noehren) ਅਤੇ ਸਰ ਦੋਰਾਬਜੀ ਟਾਟਾ (Sir Dorabji Tata) ਦੇ ਸਮਰਥਨ ਨਾਲ ਬਣੀ ਸੀ । ਇਹ ਇਕ ਗੈਰ ਸਰਕਾਰੀ ਤੇ ਗੈਰ ਮੁਨਾਫਾ ਸੰਸਥਾ ਹੈ ਜੋ ਭਾਰਤ ਦੇ ਸਮੁੱਚੇ ਰਾਜ ਦੇ ਅਧਿਕਾਰ ਖੇਤਰ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਕੋਚਾਂ ਵਾਸਤੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਕੋਰਸ ਉਪਲੱਬਧ ਕਰਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਕੋਚਾਂ ਵਾਸਤੇ ਸਰਟੀਫ਼ਿਕੇਟ ਕੋਰਸ, ਐਡਵਾਂਸ ਸਰਟੀਫ਼ਿਕੇਟ ਕੋਰਸ, ਡਿਪਲੋਮਾ ਅਤੇ ਮਾਸਟਰ ਡਿਗਰੀ ਇੰਨ ਕੋਚਿੰਗ ਵਰਗੇ ਕੋਰਸ ਉਪਲੱਬਧ ਹਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਪੁਰਸਕਾਰ ਦਾ ਕੋਈ ਇਕ ਨਿਯਮ ਲਿਖੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਸਰਕਾਰ ਸੰਬੰਧਿਤ ਖੇਡ ਫੈਡਰੇਸ਼ਨਾਂ ਤੋਂ, ਖਿਡਾਰੀ ਦੇ ਨਾਮ ਦੀ ਸੂਚੀ ਮੰਗਵਾਉਂਦੀ ਹੈ, ਜਿਸ ਦੀ ਆਖਰੀ ਮਿਤੀ 31 ਮਈ ਹੁੰਦੀ ਹੈ । ਇੱਥੇ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਦੀ ਨਾਮਜ਼ਦਗੀ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਜਿਨ੍ਹਾਂ ਨੇ ਓਲੰਪਿਕ, ਕਾਮਨਵੈਲਥ ਗੇਮਜ਼, ਏਸ਼ੀਅਨ ਖੇਡਾਂ ਵਿਚ ਮੈਡਲ ਪ੍ਰਾਪਤ ਕੀਤੇ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 11.
ਐਨ. ਐਸ. ਐਨ. ਆਈ. ਐਸ. ਪਟਿਆਲਾ ਬਾਰੇ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਨੇਤਾ ਜੀ ਸੁਭਾਸ਼ ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਨ, ਪਟਿਆਲਾ (NIS) (Netaji Subhash National Institute of Sports, Patiala) – 1959 ਵਿਚ ਭਾਰਤੀ ਖੇਡਾਂ ਦੇ ਡਿੱਗਦੇ ਮਿਆਰਾਂ ਦਾ ਅਧਿਐਨ ਕਰਨ ਲਈ ਇਕ ਕਮੇਟੀ ਬਣਾਈ ਗਈ ਸੀ । ਇਸ ਕਮੇਟੀ ਨੇ ਸਰਬ ਭਾਰਤੀ ਖੇਡ ਪਰਿਸ਼ਦ ( All India Council of Sports) ਨੂੰ ਭਾਰਤ ਵਿਚ ਇਕ ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਨ ਸਥਾਪਤ ਕਰਨ ਦੀ ਸਲਾਹ ਦਿੱਤੀ । ਬਾਅਦ ਵਿਚ 1961 ਵਿਚ ਕੇ.ਐਲ. ਸ਼ਰੀਮਾਲੀ (K.L. Sharimali) ਨੇ ਪਟਿਆਲਾ ਵਿਚ ਨੇਤਾ ਜੀ ਸੁਭਾਸ਼ ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਨ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ । ਇਸ ਦਾ ਉਦੇਸ਼ ਵਿਗਿਆਨਕ ਲੀਹਾਂ ਉੱਤੇ ਖੇਡਾਂ ਦਾ ਵਿਕਾਸ ਕਰਨਾ ਸੀ । ਇਹ ਸੰਸਥਾ ਵੱਖ-ਵੱਖ ਖੇਡਾਂ ਵਿਚ ਆਧੁਨਿਕ ਤਕਨੀਕਾਂ ਨਾਲ ਸਿਖਲਾਈ ਦਿੰਦਾ ਹੈ ਅਤੇ ਇੱਥੇ ਵੱਖ-ਵੱਖ ਖੇਡਾਂ ਦੇ ਕੋਚਿੰਗ ਡਿਪਲੋਮੇ ਅਤੇ ਰੀਫਰੈਸ਼ਰ ਕੋਰਸ ਵੀ ਕਰਵਾਏ ਜਾਂਦੇ ਹਨ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਸੰਸਥਾ ਵਿਚ ਰੀਸਰਚ ਵੀ ਹੁੰਦੀ ਹੈ ।

ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Three Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਪੋਰਟਸ ਅਥਾਰਿਟੀ ਆਫ ਇੰਡੀਆ ਤੇ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਪੋਰਟਸ ਅਥਾਰਿਟੀ ਆਫ ਇੰਡੀਆ (SAI) (Sports Authority of India) – ਸਪੋਰਟਸ ਅਥਾਰਟੀ ਆਫ ਇੰਡੀਆ ਭਾਰਤ ਸਰਕਾਰ ਦੁਆਰਾ 1984 ਵਿਚ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਸੀ ਤਾਂ ਕਿ ਖੇਡਾਂ ਦੇ ਮਿਆਰ ਨੂੰ ਦੇਸ਼ ਵਿਚ ਉੱਚਾ ਚੁੱਕਿਆ ਜਾਵੇ । ਇਸਦੇ 7 ਖੇਤਰੀ ਸੈਂਟਰ ਹਨ ਜੋ ਕਿ ਬੰਗਲੌਰ, ਭੋਪਾਲ, ਗਾਂਧੀ ਨਗਰ, ਕੋਲਕਾਤਾ, ਸੋਨੀਪਤ, ਦਿੱਲੀ, ਮੁੰਬਈ, ਅਤੇ ਇੰਫ਼ਾਲ ਵਿਚ ਸਥਿਤ ਹਨ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਗੁਹਾਟੀ ਅਤੇ ਔਰੰਗਾਬਾਦ ਵਿਚ ਦੋ ਉਪ ਕੇਂਦਰ ਵੀ ਹਨ । ਇਹ ਸੰਸਥਾ ਨੇਤਾ ਜੀ ਸੁਭਾਸ਼ ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਨ (NIS), ਲਕਸ਼ਮੀ ਬਾਈ ਨੈਸ਼ਨਲ ਕਾਲਜ ਆਫ ਫਿਜੀਕਲ ਐਜੂਕੇਸ਼ਨ ਆਦਿ ਵੱਡੀਆਂ ਸੰਸਥਾਵਾਂ ਨੂੰ ਚਲਾਉਂਦੀ ਹੈ । ਇਸ ਸੰਸਥਾ ਦਾ ਮੁੱਖ ਉਦੇਸ਼ ਖੇਡਾਂ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਸਹੂਲਤਾਂ ਨੂੰ ਉਚਿਤ ਵਰਤੋਂ ਵਿਚ ਲਿਆਉਣਾ ਅਤੇ ਖੇਡਾਂ ਦੀ ਉੱਨਤੀ ਅਤੇ ਖੇਡ ਦਾ ਪ੍ਰਬੰਧ ਚਲਾਉਣਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਰਾਜ ਕੁਮਾਰੀ ਕੋਚਿੰਗ ਸਕੀਮ ਕਿਵੇਂ ਪੇਸ਼ ਕੀਤੀ ਗਈ ? .
ਉੱਤਰ-
ਰਾਜ ਕੁਮਾਰੀ ਅੰਮ੍ਰਿਤ ਕੌਰ ਕੋਚਿੰਗ ਸਕੀਮ 1953 ਵਿਚ ਸ਼ੁਰੂ ਕੀਤੀ ਗਈ ਸੀ । ਅੱਠ ਸਾਲਾਂ ਦੇ ਬਾਅਦ ਇਸ ਨੂੰ ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਨ ਵਿਚ ਮਿਲਾ ਦਿੱਤਾ ਗਿਆ । ਇਸ ਸਕੀਮ ਦਾ ਉਦੇਸ਼ ਖਿਡਾਰੀਆਂ ਨੂੰ ਸਿਖਲਾਈ ਪ੍ਰਦਾਨ ਕਰਨਾ ਸੀ ।
ਰਾਜ ਕੁਮਾਰੀ ਅੰਮ੍ਰਿਤ ਕੌਰ ਕੋਚਿੰਗ ਸਕੀਮ ਦੇ ਉਦੇਸ਼

1. ਸਾਲਾਨਾ ਕੋਚਿੰਗ ਕੈਂਪ ਅਤੇ ਟੀਮਾਂ ਨੂੰ ਮੁਕਾਬਲਿਆਂ ਲਈ ਤਿਆਰ ਕਰਨਾ ।
2. ਕੋਚਿੰਗ, ਕਲੀਨਿਕ ਅਤੇ ਮੁਕਾਬਲਿਆਂ ਆਦਿ ਦੀ ਤਿਆਰੀ ਕਰਵਾਉਣ ਲਈ ਫੈਡਰੇਸ਼ਨਸ ਨੂੰ ਸਹਾਇਤਾ ਕਰਨਾ
3. ਕੋਚਾਂ ਵਾਸਤੇ ਰੀਫਰੈਸ਼ਰ ਕੋਰਸ ਲਗਵਾਉਣੇ ਅਤੇ ਬਾਹਰਲੇ ਦੇਸ਼ਾਂ ਦੇ ਮਾਹਿਰਾਂ ਨੂੰ ਬੁਲਾਉਣਾ ।
4. ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਦੇ ਉਚਤਮ ਵਿਕਾਸ ਲਈ ਮਦਦ ਅਤੇ ਅਗਵਾਈ ਦੇਣਾ ।
5. ਰਾਜ ਸਰਕਾਰ ਅਤੇ ਸੰਸਥਾਵਾਂ ਵਿਚ ਤਾਲਮੇਲ ਪੈਦਾ ਕਰਨਾ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਕੂਲੀ ਅਧਿਆਪਕਾਂ ਲਈ ਵੱਖ-ਵੱਖ ਯੋਗਤਾਵਾਂ ਕੀ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਸਰੀਰਕ ਸਿੱਖਿਆ ਨੂੰ ਅਧਿਆਪਨ ਦੇ ਤੌਰ ਤੇ ਅਪਣਾਉਣ ਲਈ ਆਪਣੇ ਕੋਲ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਕਾਲਜ ਜਾਂ ਯੂਨੀਵਰਸਿਟੀ ਤੋਂ ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਸਰਟੀਫਿਕੇਟ, ਡਿਗਰੀ ਜਾਂ ਡਿਪਲੋਮਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਸਰੀਰਕ ਸਿੱਖਿਆ ਲਈ ਇਸ ਖੇਤਰ ਵਿਚ ਕਈ ਮੌਕੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਡਿਗਰੀਆਂ ਦੀਆਂ ਪ੍ਰਾਪਤੀਆਂ ਤੋਂ ਬਾਅਦ ਉਹ ਸਕੂਲ ਵਿਚ ਅਧਿਆਪਕ ਵੀ ਹੋ ਸਕਦੇ ਹਨ ।

ਉਪਰੋਕਤ ਡਿਗਰੀ ਪ੍ਰਾਪਤੀ ਲਈ ਸਿੱਖਿਆਰਥੀ ਨੇ 12ਵੀਂ ਪਾਸ ਕੀਤੀ ਹੋਵੇ ਅਤੇ ਨਾਲ ਕੋਈ ਖੇਡ ਪ੍ਰਾਪਤੀ ਅਤੇ ਉਪਰੋਕਤ ਕੋਰਸ ਲਈ ਇਨਟਰੈਂਸ ਪੇਪਰ ਪਾਸ ਕੀਤਾ ਹੋਵੇ ।

ਪ੍ਰਸ਼ਨ 4.
ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਪੇਸ਼ੇ ਵਜੋਂ “ਪੱਤਰਕਾਰੀ” ਨੂੰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਇਕ ਖੇਡ ਪੱਤਰਕਾਰ ਦੇ ਰੂਪ ਵਿਚ (As a Sports Journalist) – ਦੁਨੀਆਂ ਭਰ ਵਿਚ ਖੇਡਾਂ ਨੂੰ ਬੜੇ ਧਿਆਨ ਨਾਲ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ । ਅੱਜ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਲੋਕ ਮੀਡੀਆ, ਖਬਰਾਂ, ਮੈਗਜੀਨਾਂ ਵਿਚ ਖੇਡ ਪੱਤਰਕਾਰ ਦੇ ਰੂਪ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ ਇਸ ਲਈ ਇਹ ਇਕ ਵਧੀਆ ਕੈਰੀਅਰ ਵਿਕਲਪ ਦੇ ਰੂਪ ਵਿਚ ਆ ਰਿਹਾ ਹੈ । ਖੇਡ ਪੱਤਰਕਾਰ ਨੂੰ ਮਾਸਿਕ ਸੰਚਾਰ (Mass Communication) ਵਿਚ ਡਿਗਰੀ ਦਾ ਡਿਪਲੋਮਾ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਹਨਾਂ ਡਿਗਰੀਆਂ ਵਾਸਤੇ ਖੇਡ ਪੱਤਰਕਾਰ ਨੇ 12ਵੀਂ ਪਾਸ ਕੀਤੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਉਸ ਕੋਲ ਵੱਖ-ਵੱਖ ਖੇਡ ਦਾ ਤੇ ਖੇਡ ਦੇ ਪ੍ਰਦਰਸ਼ਨ ਦਾ ਗਿਆਨ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਉਸਨੂੰ ਮੀਡੀਆ ਉਤਪਾਦਨ (production) ਅਤੇ ਪ੍ਰਸਾਰਣ ਬਾਰੇ ਜਾਣਕਾਰੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਅਵਾਰਡ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਪੁਰਸਕਾਰ (Rajiv Gandhi Sports Awards) – ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਪੁਰਸਕਾਰ ਸਾਬਕਾ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਰਾਜੀਵ ਗਾਂਧੀ ਦੀ ਯਾਦ ਵਿਚ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਹ ਸਭ ਤੋਂ ਵੱਡੇ ਰੈਂਕ ਦਾ ਰਾਸ਼ਟਰੀ ਪੁਰਸਕਾਰ ਹੈ ਅਤੇ ਇਹ ਖਿਡਾਰੀਆਂ ਦੇ ਮਨੋਬਲ ਅਤੇ ਵਿਸ਼ਵਾਸ ਨੂੰ ਉਤਸਾਹਿਤ ਕਰਨ ਲਈ ਇਹ 1991 ਵਿਚ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ । ਇਹ ਪੁਰਸਕਾਰ ਯੁਵਾ ਮਾਮਲਿਆਂ ਅਤੇ ਖੇਡ ਮੰਤਰਾਲੇ ਦੁਆਰਾ ਖਿਡਾਰੀਆਂ ਨੂੰ ਭਾਰਤ ਵਿਚ ਖੇਡਾਂ ਵਿਚ ਸ਼ਾਨਦਾਰ ਪ੍ਰਦਰਸ਼ਨ ਲਈ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਪੁਰਸਕਾਰ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੇ 7.5 ਲੱਖ ਦਾ ਨਕਦ ਇਨਾਮ, ਅਤੇ ਤਮਗਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ | ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਇਹ ਪੁਰਸਕਾਰ ਵਿਸ਼ਵਨਾਥਨ ਆਨੰਦ (Vishwnathan Anand) ਨੇ 1992-1993 ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤਾ ਅਤੇ ਔਰਤਾਂ ਵਿਚ ਕਰਨਮ ਮਲੇਸ਼ਵਰੀ ਨੂੰ ਇਹ ਪੁਰਸਕਾਰ 1995-96 ਵਿਚ ਮਿਲਿਆ | ਪੰਕਜ ਅਡਵਾਨੀ ਇਕ ਅਜਿਹੇ ਪਹਿਲੇ ਖਿਡਾਰੀ ਹੋਏ ਹਨ ਜਿਨ੍ਹਾਂ ਨੂੰ ਦੋ ਖੇਡਾਂ ਸਨੁਕਰ (Snooker) ਅਤੇ ਬਿਲੀਅਰਡਜ਼ (Billiards) ਲਈ ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਪੁਰਸਕਾਰ ਮਿਲਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਖਿਡਾਰੀਆ ਨੂੰ ਦਿੱਤੇ ਜਾਣ ਵਾਲੇ ਸਭ ਤੋਂ ਵੱਡੇ ਅਵਾਰਡ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਖਿਡਾਰੀਆਂ ਨੂੰ ਸਭ ਤੋਂ ਵੱਡਾ ਅਵਾਰਡ ਅਰਜੁਨ ਅਵਾਰਡ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਪੁਰਸਕਾਰ 1961 ਵਿਚ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ ਸੀ ਅਤੇ ਇਹ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੇ ਲਗਾਤਾਰ ਚਾਰ ਸਾਲ ਤਕ ਕੌਮੀ ਅਤੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਪੱਧਰ ਜਿਵੇਂ ਕਿ ਓਲੰਪਿਕ ਖੇਡਾਂ, ਏਸ਼ੀਅਨ ਖੇਡਾਂ, ਕਾਮਨਵੈਲਥ ਅਤੇ ਰਾਸ਼ਟਰੀ ਪੱਧਰ ਤੇ ਬੇਹਤਰੀਨ ਪ੍ਰਦਰਸ਼ਨ ਕੀਤਾ ਹੋਏ । ਇਸ ਅਵਾਰਡ ਦੇ ਤਹਿਤ ਇਕ ਵਾਫੀ (ਅਰਜਨ ਦਾ ਕਾਂਸੀ ਦਾ ਬੁੱਤ) ਅਤੇ 5 ਲੱਖ ਰੁਪਏ ਨਕਦ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ ।

ਇਹ ਅਵਾਰਡ ਖੇਡ ਮੰਤਰਾਲੇ ਵਜੋਂ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ 1961 ਵਿਚ ਸਭ ਤੋਂ ਪਹਿਲਾਂ 6 ਖਿਡਾਰੀਆਂ ਨੂੰ ਇਹ ਅਵਾਰਡ ਦਿੱਤਾ ਗਿਆ । ਇਹ ਖਿਡਾਰੀ ਸਲੀਮ ਦੁਰਾਨੀ (Saleem Durrani) ਕ੍ਰਿਕਟ, ਗੁਰਬਚਨ ਸਿੰਘ ਰੰਧਾਵਾ (Gurbachan Singh Randhawa) ਐਥਲੈਟਿਕਸ, ਸਰਬਜੀਤ ਸਿੰਘ (Sarabjit Singh) ਬਾਸਕੇਟਬਾਲ, ਮੈਨੁਅਲ ਮੋਰਾਨ (Manuel Aaron ਸ਼ਤਰੰਜ, ਨੰਦੁ ਟੇਕ (Nandhu Natekar) ਬੈਡਮਿੰਟਨ ਅਤੇ ਐਲ.ਬੀ. ਡਿਸਜਾ (L.B. D’souza) ਬਾਕਸਿੰਗ, ਮੀਨਾ ਸ਼ਾਹ (Meena Shah) ਬੈਡਮਿੰਟਨ ਪਹਿਲੀ ਮਹਿਲਾ ਸੀ ਜਿਸ ਨੂੰ 1962 ਵਿਚ ਇਹ ਅਵਾਰਡ ਦਿੱਤਾ ਗਿਆ ।

ਪ੍ਰਸ਼ਨ 7.
ਕੋਚਾਂ ਦੇ ਯੋਗਦਾਨ ਲਈ ਕਿਹੜਾ ਅਵਾਰਡ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ? ਅਵਾਰਡ ਬਾਰੇ ਕੁਝ ਲਾਈਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਖੇਡਾਂ ਵਿਚ ਕੋਚਾਂ ਦੇ ਯੋਗਦਾਨ ਦੀ ਪਛਾਣ ਕਰਨ ਲਈ, ਭਾਰਤ ਸਰਕਾਰ ਨੇ ਦਰੋਣਾਚਾਰੀਆ ਪੁਰਸਕਾਰ ਨੂੰ ਦੇਣ ਦਾ ਫੈਸਲਾ ਕੀਤਾ ਅਤੇ ਇਸ ਪੁਰਸਕਾਰ ਦਾ ਨਾਮ ਅਰਜੁਨ ਦੇ ਗੁਰੂ ਦਰੋਣਾਚਾਰੀਆ ਦੇ ਨਾਮ ਤੇ ਰੱਖਿਆ ਗਿਆ ।ਇਕ ਸ਼ਾਨਦਾਰ ਗੁਰੂ ਜਿਸ ਨੇ ਪਾਠਕਾਂ ਨੂੰ ਸਿੱਖਿਅਤ ਕੀਤਾ ਸੀ । ਇਹ ਪੁਰਸਕਾਰ ਉਨ੍ਹਾਂ ਕੋਚਾਂ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਦੇ ਖਿਡਾਰੀਆਂ ਨੇ ਰਾਸ਼ਟਰੀ ਅਤੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਖੇਡ ਮੁਕਬਾਲਿਆਂ ਵਿਚ ਤਮਗਾ ਜਿੱਤਿਆ ਹੋਵੇ । ਇਸ ਅਵਾਰਡ ਦੇ ਜੇਤੂ ਨੂੰ ਦਰੋਣਾਚਾਰੀਆ ਦੀ ਮੂਰਤੀ ਅਤੇ 5 ਲੱਖ ਰੁਪਏ ਦਾ ਨਕਦ ਇਨਾਮ ਦੇ ਨਾਲ ਸਰਟੀਫਿਕੇਟ ਪੇਸ਼ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਭਾਲਚੰਦਰ ਭਾਸਕਰ ਭਾਗਵਤ ਰੈਸਲਿੰਗ), ਉਮ ਪ੍ਰਕਾਸ਼ ਭਾਰਦਵਾਜ ਬਾਕਸਿੰਗ), ਓ.ਐਮ ਨੰਬੀਅਰ (ਐਥਲੇਟਿਕਸ) ਆਦਿ ਨੂੰ 1988 ਵਿਚ ਪਹਿਲੀ ਵਾਰ ਪੁਰਸਕਾਰ ਨਾਲ ਸਮਾਨਿਤ ਕੀਤਾ ਗਿਆ ।

ਪ੍ਰਸ਼ਨ 8.
ਧਿਆਨ ਚੰਦ ਅਵਾਰਡ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਖੇਡਾਂ ਦੇ ਖੇਤਰ ਵਿਚ ਇਹ ਸਭ ਤੋਂ ਵੱਡਾ ਪੁਰਸਕਾਰ ਹੈ ਇਸ ਅਵਾਰਡ ਦਾ ਨਾਮ ਹਾਕੀ ਦੇ ਜਾਦੂਗਰ ਧਿਆਨਚੰਦ ਦੇ ਨਾਮ ਤੇ ਰੱਖਿਆ ਗਿਆ ਹੈ ਜੋ ਕਿ ਭਾਰਤੀ ਸੈਨਾ ਦੇ ਸਿਪਾਹੀ ਸਨ ਤੇ ਨਾਲ ਹੀ ਹਾਕੀ ਦੇ ਉੱਘੇ ਖਿਡਾਰੀ, ਜਿਨ੍ਹਾਂ ਨੇ ਆਪਣੇ 20 ਸਾਲ ਦੇ ਕੈਰੀਅਰ ਵਿਚ ਤਕਰੀਬਨ 1000 ਤੋਂ ਵੱਧ ਗੋਲ ਬਣਾਏ ਸਨ ।

ਇਹ ਅਵਾਰਡ 2002 ਵਿਚ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ ਸੀ ਅਤੇ ਹਰ ਸਾਲ ਖੇਡ ਮੰਤਰਾਲੇ ਵਲੋਂ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਅਵਾਰਡ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੇ ਨੂੰ ਉਹਨਾਂ ਦੇ ਖੇਡਾਂ ਵਿਚ ਪ੍ਰਦਰਸ਼ਨ ਅਤੇ ਯੋਗਦਾਨ ਦੇ ਅਧਾਰ ਤੇ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਅਵਾਰਡ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ-
ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਅਵਾਰਡ ਪੰਜਾਬ ਸਰਕਾਰ ਦੁਆਰਾ ਸਿੱਖ ਰਾਜ ਦੇ ਆਗੁ ਦੇ ਨਾਂ ਤੇ 1978 ਵਿਚ ਸਥਾਪਿਤ ਕੀਤਾ ਸੀ । ਇਸ ਅਵਾਰਡ ਵਿਚ ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਦੀ ਟ੍ਰਾਫੀ ਤੇ 5 ਲੱਖ ਰੁਪਏ ਦੀ ਨਕਦ ਰਕਮ (2018 ਪਾਲਿਸੀ ਦੇ ਅਨੁਸਾਰ ਰਕਮ ਵਾਧਾ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । 2017 ਤੱਕ ਇਹ ਰਾਸ਼ੀ ਇੱਕ ਲੱਖ ਰੁਪਏ ਸੀ । ਇਹ ਪੁਰਸਕਾਰ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਪੱਧਰ ਦੇ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਹਿੱਸਾ ਲਿਆ ਹੋਵੇ । ਸ: ਪਰਗਟ ਸਿੰਘ ਪਹਿਲੇ ਵਿਅਕਤੀ ਸਨ ਜਿਨ੍ਹਾਂ ਨੇ ਇਹ ਪੁਰਸਕਾਰ ਪ੍ਰਾਪਤ ਕੀਤਾ ।

ਪ੍ਰਸ਼ਨ 10.
ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਅਵਾਰਡ ਲਈ ਕੀ ਨਿਯਮ ਹਨ ?
ਉੱਤਰ-

1. ਜਿਸ ਖਿਡਾਰੀ ਨੂੰ ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ, ਅਰਜੁਨ ਅਵਾਰਡ ਮਿਲਿਆ ਹੋਵੇ ਅਤੇ ਉਹ ਪੰਜਾਬ ਦਾ ਰਹਿਣ ਵਾਲਾ ਹੋਵੇ ਉਸਨੂੰ ਇਹ ਪੁਰਸਕਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
2. ਜਿਸ ਖਿਡਾਰੀ ਨੇ ਪੰਜ ਸਾਲ ਦੇ ਕੈਰੀਅਰ ਵਿਚ ਕੁੱਲ 40 ਅੰਕ ਪ੍ਰਾਪਤ ਕੀਤੇ ਹੋਣ ।
3. ਇਹ ਪੁਰਸਕਾਰ 1996 ਤੋਂ 2005 ਤੱਕ ਮੁਅੱਤਲ ਕਰ ਦਿੱਤਾ ਗਿਆ ਸੀ ਅਤੇ 2006 ਵਿਚ ਇਸ ਨੂੰ ਦੁਬਾਰਾ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ ਸੀ ।

ਪ੍ਰਸ਼ਨ 11.
ਰਾਜ ਕੁਮਾਰੀ ਅੰਮ੍ਰਿਤ ਕੌਰ ਕੋਚਿੰਗ ਸਕੀਮ ਦੇ ਉਦੇਸ਼ ਕੀ ਸਨ ?
ਉੱਤਰ-

1. ਸਾਲਾਨਾ ਕੋਚਿੰਗ ਕੈਂਪ ਅਤੇ ਟੀਮਾਂ ਨੂੰ ਮੁਕਾਬਲਿਆਂ ਲਈ ਤਿਆਰ ਕਰਨਾ ।
2. ਕੋਚਿੰਗ, ਕਲੀਨਿਕ ਅਤੇ ਮੁਕਾਬਲਿਆਂ ਆਦਿ ਦੀ ਤਿਆਰੀ ਕਰਵਾਉਣ ਲਈ ਫੈਡਰੇਸ਼ਨ ਨੂੰ ਸਹਾਇਤਾ ਕਰਨਾ ।
3. ਕੋਚਾਂ ਵਾਸਤੇ ਰੀਫਰੈਸ਼ਰ ਕੋਰਸ ਲਗਵਾਉਣੇ ਅਤੇ ਬਾਹਰਲੇ ਦੇਸ਼ਾਂ ਦੇ ਮਾਹਿਰਾਂ ਨੂੰ ਬੁਲਾਉਣਾ ।
4. ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਦੇ ਉੱਚਤਮ ਵਿਕਾਸ ਲਈ ਮਦਦ ਅਤੇ ਅਗਵਾਈ ਦੇਣਾ ।
5. ਰਾਜ ਸਰਕਾਰ ਅਤੇ ਸੰਸਥਾਵਾਂ ਵਿਚ ਤਾਲਮੇਲ ਪੈਦਾ ਕਰਨਾ ।

ਪ੍ਰਸ਼ਨ 12.
ਸਪੋਰਟਸ ਅਥਾਰਿਟੀ ਆਫ਼ ਇੰਡੀਆ ਦੀ ਖੇਡਾਂ ਵਿਚ ਕੀ ਭੂਮਿਕਾ ਹੈ ?
ਉੱਤਰ-
ਸਪੋਰਟਸ ਅਥਾਰਟੀ ਆਫ ਇੰਡੀਆ ਭਾਰਤ ਸਰਕਾਰ ਦੁਆਰਾ 1984 ਵਿਚ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਸੀ ਤਾਂ ਕਿ ਖੇਡਾਂ ਦੇ ਮਿਆਰ ਨੂੰ ਦੇਸ਼ ਵਿਚ ਉੱਚਾ ਚੁੱਕਿਆ ਜਾਵੇ । ਇਸਦੇ 7 ਖੇਤਰੀ ਸੈਂਟਰ ਹਨ ਜੋ ਕਿ ਬੰਗਲੌਰ, ਭੋਪਾਲ, ਗਾਂਧੀ ਨਗਰ, ਕੋਲਕਾਤਾ, ਸੋਨੀਪਤ, ਦਿੱਲੀ, ਮੁੰਬਈ ਅਤੇ ਇੰਫ਼ਾਲ ਵਿਚ ਸਥਿਤ ਹਨ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਗੁਹਾਟੀ ਅਤੇ ਔਰੰਗਾਬਾਦ ਵਿਚ ਦੋ ਉਪ ਕੇਂਦਰ ਵੀ ਹਨ । ਇਹ ਸੰਸਥਾ ਨੇਤਾ ਜੀ ਸੁਭਾਸ਼ ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਨ (NIS), ਲਕਸ਼ਮੀ ਬਾਈ ਨੈਸ਼ਨਲ ਕਾਲਜ ਆਫ਼ ਫਿਜੀਕਲ ਐਜੂਕੇਸ਼ਨ ਆਦਿ ਵੱਡੀਆਂ ਸੰਸਥਾਵਾਂ ਨੂੰ ਚਲਾਉਂਦੀ ਹੈ । ਇਸ ਸੰਸਥਾ ਦਾ ਮੁੱਖ ਉਦੇਸ਼ ਖੇਡਾਂ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਸਹੂਲਤਾਂ ਨੂੰ ਉੱਚਿਤ ਵਰਤੋਂ ਵਿਚ ਲਿਆਉਣਾ ਅਤੇ ਖੇਡਾਂ ਦੀ ਉੱਨਤੀ ਅਤੇ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਚਲਾਉਣਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਆਈ. ਓ. ਏ. (OA) ਦੇ ਕੰਮਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਆਈ. ਓ. ਏ. (IOA) ਦੇ ਕੰਮ (Functions of IOA)-

1. ਐਸੋਸੀਏਸ਼ਨ ਦੀ ਨੀਤੀ ਨੂੰ ਤਿਆਰ ਅਤੇ ਲਾਗੂ ਕਰਨਾ ।
2. ਸੰਸਥਾ ਦੇ ਸੰਵਿਧਾਨ ਦੇ ਉਪਬੰਧਾਂ ਦੇ ਅਨੁਸਾਰ ਘੱਟੋ-ਘੱਟ ਚਾਰ ਸਾਲਾਂ ਵਿਚ ਘੱਟੋ-ਘੱਟ ਇਕ ਵਾਰ ਅਹੁਦੇਦਾਰਾਂ ਅਤੇ ਕਾਰਜਸ਼ੀਲ ਕੌਂਸਲ ਦੀ ਚੋਣ ਕਰਵਾਉਣਾ ।
3. ਐਸੋਸੀਏਸ਼ਨ ਦੇ ਫੰਡ ਅਤੇ ਹੋਰ ਸੰਪੱਤੀਆਂ ਨੂੰ ਰੱਖਣਾ ਅਤੇ ਕੰਟਰੋਲ ਕਰਨਾ ।
4. ਜਦੋਂ ਜ਼ਰੂਰੀ ਹੋਵੇ ਤਾਂ ਕਮੇਟੀ ਜਾਂ ਉਪ ਕਮੇਟੀਆਂ ਦੀ ਨਿਯੁਕਤੀ ਕਰਨਾ ।
5. ਅੰਤਰਰਾਸ਼ਟਰੀ ਓਲੰਪਿਕ ਕਮੇਟੀ ਦੇ ਪਾਸ ਕੀਤੇ ਨਿਯਮਾਂ ਨੂੰ ਲਾਗੂ ਕਰਵਾਉਣਾ ।

ਪ੍ਰਸ਼ਨ 14.
ਅਧਿਆਪਨ ਕਿੱਤੇ ਲਈ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਅਧਿਆਪਕਾਂ ਵਾਸਤੇ ਕੀ ਵਿਕਲਪ ਹਨ ?
ਉੱਤਰ-
ਇਕ ਅਧਿਆਪਨ ਦੇ ਕਿੱਤੇ ਵਜੋਂ ਕੈਰੀਅਰ (As a Teaching Profession) – ਸਰੀਰਕ ਸਿੱਖਿਆ ਨੂੰ ਅਧਿਆਪਨ ਦੇ ਤੌਰ ਤੇ ਅਪਣਾਉਣ ਲਈ ਆਪਣੇ ਕੋਲ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਕਾਲਜ ਜਾਂ ਯੂਨੀਵਰਸਿਟੀ ਤੋਂ ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਸਰਟੀਫਿਕੇਟ, ਡਿਗਰੀ ਜਾਂ ਡਿਪਲੋਮਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਉਹਨਾਂ ਨੂੰ ਸੰਬੰਧਿਤ ਖੇਤਰ ਵਿਚ ਬੀ.ਪੀ.ਈ., ਬੀ.ਪੀ.ਐੱਡ., ਐੱਮ.ਪੀ.ਐੱਡ., ਐੱਮ.ਫਿਲ, ਜਾਂ ਫਿਰ ਉੱਚੀ ਡਿਗਰੀ ਪੀ.-ਐੱਚ.ਡੀ. ਕੀਤੀ ਹੋਈ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ | ਸਰੀਰਕ ਸਿੱਖਿਆਵਾਦੀ ਲਈ ਇਸ ਖੇਤਰ ਵਿਚ ਕਈ ਮੌਕੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਡਿਗਰੀਆਂ ਦੀਆਂ ਪ੍ਰਾਪਤੀਆਂ ਤੋਂ ਬਾਅਦ ਉਹ ਸਕੂਲ ਵਿਚ ਅਧਿਆਪਕ ਜਾਂ ਕਾਲਜ ਵਿਚ ਪ੍ਰੋਫ਼ੈਸਰ ਵੀ ਹੋ ਸਕਦੇ ਹਨ ।

ਪੰਜ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ ਤੋਂ (Five Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਕੈਰੀਅਰ ਦੇ ਵਿਕਲਪਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਰੀਰਕ ਸਿੱਖਿਆ ਇਕ ਅਜਿਹੀ ਸਿੱਖਿਆ ਹੈ ਜੋ ਕਿ ਸਰੀਰਕ ਗਤੀਵਿਧੀਆਂ, ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ, ਜੀਵਨ ਸ਼ੈਲੀ, ਖੇਡਾਂ ਅਤੇ ਅੰਤਰ-ਨਿਜੀ ਹੁਨਰ ਦੇ ਰਾਹੀਂ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ | ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਵਿਚ ਕੈਰੀਅਰ ਦੇ ਮੌਕੇ ਦਿਨੋ-ਦਿਨ ਭਾਰਤ ਅਤੇ ਵਿਦੇਸ਼ਾਂ ਵਿਚ ਵੱਧ ਰਹੇ ਹਨ । ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਵਿਸ਼ੇ ਵਿਚ ਕੈਰੀਅਰ ਬਣਾਉਣ ਦਾ ਵਿਕਲਪ ਅਸਾਨ ਨਹੀਂ ਹੈ । ਇਸ ਵਿਚ ਭਾਰਤ ਦੀਆਂ ਕਈ ਸਰਕਾਰੀ ਸੰਸਥਾਵਾਂ ਜਿਵੇਂ ਸਪਰੋਟਸ ਅਥਾਰਿਟੀ ਆਫ ਇੰਡੀਆ, ਰਾਸ਼ਟਰੀ ਖੇਡ ਸੰਸਥਾਵਾਂ, ਵੱਖ-ਵੱਖ ਯੂਥ ਸੇਵਾਵਾਂ ਅਤੇ ਖੇਡ ਵਿਭਾਗ, ਰੇਲਵੇਜ਼, ਬੈਂਕ, ਭਾਰਤੀ ਏਅਰਲਾਨੀਜ, ਸੂਬਾ ਪੁਲਿਸ ਵਰਗੀਆਂ ਸੰਸਥਾਵਾਂ ਬਹੁਤ ਸਾਡੀਆਂ ਨੌਕਰੀਆਂ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ । ਇਹ ਨੌਕਰੀਆਂ ਖੇਡ ਕੋਟੇ ਦੇ ਅਧੀਨ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਅੱਜ ਦੇ ਦੌਰ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਨੌਕਰੀਆਂ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਖੇਤਰ ਮੌਕੇ ਪ੍ਰਦਾਨ ਕਰ ਰਹੇ ਹਨ | ਅਸੀ ਇਹਨਾਂ ਵਿਕਲਪਾਂ ਨੂੰ ਹੇਠ ਲਿਖੀਆਂ ਸ਼੍ਰੇਣੀਆਂ ਵਿਚ ਵੰਡ ਸਕਦੇ ਹਾਂ-

1. ਇਕ ਅਧਿਆਪਨ ਦੇ ਕਿੱਤੇ ਵਜੋਂ ਕੈਰੀਅਰ (As a teaching Profession) – ਸਰੀਰਕ ਸਿੱਖਿਆ ਨੂੰ ਅਧਿਆਪਨ ਦੇ ਤੌਰ ਤੇ ਅਪਣਾਉਣ ਲਈ ਆਪਣੇ ਕੋਲ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਕਾਲਜ ਜਾਂ ਯੂਨੀਵਰਸਿਟੀ ਤੋਂ ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਸਰਟੀਫਿਕੇਟ, ਡਿਗਰੀ ਜਾਂ ਡਿਪਲੋਮਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਉਹਨਾਂ ਨੂੰ ਸੰਬੰਧਿਤ ਖੇਤਰ ਵਿਚ ਬੀ.ਪੀ.ਈ., ਬੀ.ਪੀ.ਐੱਡ, ਐਮ.ਪੀ.ਐੱਡ., ਐਮ.ਫਿਲ. ਜਾਂ ਫਿਰ ਉੱਚੀ ਡਿਗਰੀ ਪੀ-ਐੱਚ. ਡੀ ਕੀਤੀ ਹੋਈ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ | ਸਰੀਰਕ ਸਿੱਖਿਆਵਾਦੀ ਲਈ ਇਸ ਖੇਤਰ ਵਿਚ ਕਈ ਮੌਕੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਡਿਗਰੀਆਂ ਦੀਆਂ ਪ੍ਰਾਪਤੀਆਂ ਤੋਂ ਬਾਅਦ ਉਹ ਸਕੂਲ ਵਿਚ ਅਧਿਆਪਕ ਜਾਂ ਕਾਲਜ ਵਿਚ ਪ੍ਰੋਫੈਸਰ ਵੀ ਹੋ ਸਕਦੇ ਹਨ ।

ਉਪਰੋਕਤ ਡਿਗਰੀ ਪ੍ਰਾਪਤੀ ਲਈ ਸਿੱਖਿਆਰਥੀ ਨੇ 12ਵੀਂ ਪਾਸ ਕੀਤੀ ਹੋਵੇ ਅਤੇ ਨਾਲ ਕੋਈ ਖੇਡ ਪ੍ਰਾਪਤੀ ਅਤੇ ਉਪਰੋਕਤ ਕੋਰਸ ਲਈ ਇਨਟਰੈਸ ਪੇਪਰ ਪਾਸ ਕੀਤਾ ਹੋਵੇ ।

2. ਇਕ ਕੋਚ ਦੇ ਕਿੱਤੇ ਵਜੋਂ (As a coaching Profession) – ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਕੋਚਿੰਗ ਦਾ ਇਕ ਵੱਖਰਾ ਖੇਤਰ ਹੈ । ਦੁਨੀਆਂ ਵਿਚ ਕਈ ਖੇਡਾਂ ਖੇਡੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਹਰੇਕ ਖੇਡ ਲਈ ਵਿਸ਼ੇਸ਼ ਕੋਚਿੰਗ ਦੀ ਲੋੜ ਹੈ । ਕਿਸੇ ਖਾਸ ਖੇਡ ਵਿਚ ਕੋਚਿੰਗ ਦਾ ਡਿਪੋਮਾ ਕਰਨ ਤੋਂ ਬਾਅਦ ਇਕ ਵਿਅਕਤੀ ਨੂੰ ਇਕ ਕੋਚ ਵਜੋਂ ਨੌਕਰੀ ਮਿਲਦੀ ਹੈ । ਰਾਸ਼ਟਰੀ ਜਾਂ ਅੰਤਰਰਾਸ਼ਟਰੀ ਟੀਮ ਦੀ ਕੋਚਿੰਗ ਤੋਂ ਇਲਾਵਾ ਕੋਚ ਕੋਲ ਅਜਿਹੇ ਮੌਕੇ ਹੁੰਦੇ ਹਨ । ਜਿੱਥੇ ਉਹ ਕੋਚਿੰਗ ਕਰ ਸਕਦਾ ਹੈ, ਜਿਵੇਂ ਸਕੂਲ, ਕਾਲਜ ਅਤੇ ਕਲੱਬ ਆਦਿ ।

ਉਹ ਆਪਣੀ ਖੁਦ ਦੀ ਸਪੋਰਟਸ ਅਕੈਡਮੀ ਚਲਾ ਸਕਦੇ ਹਨ । ਇਸ ਵਾਸਤੇ ਉਸ ਕੋਲ ਐੱਨ.ਆਈ.ਐੱਸ. ਡਿਪਲੋਮਾ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਉਹ ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਵੀ ਆਪਣੀ ਡਿਗਰੀ ਪੂਰੀ ਕਰ ਸਕਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਬੀ.ਪੀ.ਐਡ. ਅਤੇ ਐਮ.ਪੀ ਐਡ ਆਦਿ । ਐਨ.ਆਈ.ਐਸ. ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਕੋਚਿੰਗ ਡਿਪਲੋਮੇ ਹਨ । ਇਹ ਹੇਠ ਲਿਖੇ ਹਨ-

1. ਇਕ ਖੇਡ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਦੇ ਤੌਰ ਤੇ (As a Sports Physiotherapist) – ਜੇ ਵਿਅਕਤੀ ਨੂੰ ਖੇਡਾਂ ਵਿਚ ਲੱਗਣ ਵਾਲੀਆਂ ਸੱਟਾਂ ਅਤੇ ਪ੍ਰਬੰਧਨ ਦੀ ਜਾਣਕਾਰੀ ਹੋਏ ਤਾਂ ਉਹ ਇਸ ਕਿੱਤੇ ਨੂੰ ਖੇਡ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਦੇ ਤੌਰ ਤੇ ਅਪਣਾ ਸਕਦੇ ਹਨ । ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਬਣਨ ਦੀ ਯੋਗਤਾ ਡਿਪਲੋਮਾ, ਬੈਚਲਰ ਆਫ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਬੀ.ਐੱਸ.ਸੀ., (B.Sc.) ਇਨ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਜਾਂ ਮਾਸਿਕ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਲਾਜ਼ਮੀ ਹੈ । ਕੈਰੀਅਰ ਦੇ ਤੌਰ ‘ਤੇ ਫਿਜਿਊਥੈਰੇਪਿਸਟ ਲਈ ਸ਼ਾਨਦਾਰ ਮੌਕੇ ਹਨ । ਉਹ ਕਈ ਖੇਡ ਸੰਸਥਾਵਾਂ ਨਾਲ ਜੁੜ ਸਕਦੇ ਹਨ । ਰਾਸ਼ਟਰੀ ਟੀਮਾਂ ਜਾਂ ਫਿਰ ਨਿੱਜੀ ਫਿਜਿਉਥੈਰੇਪਿਸਟ ਦੇ ਤੌਰ ‘ਤੇ ਵੀ ਕੰਮ ਕਰ ਸਕਦੇ ਹਨ ਕਿਉਂਕਿ ਖੇਡ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਜਾਂ ਫਿਰ ਅਭਿਆਸ ਦੌਰਾਨ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸੱਟਾਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਲੱਗਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ ਅਤੇ ਇਹਨਾਂ ਦੇ ਇਲਾਜ ਵਾਸਤੇ ਭੌਤਿਕ-ਚਿਕਿਤਸਾ ਦੇ ਮਾਹਿਰਾਂ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ।

2. ਇਕ ਖੇਡ ਪੱਤਰਕਾਰ ਦੇ ਰੂਪ ਵਿਚ (As a Sports Journalist) – ਦੁਨੀਆਂ ਭਰ ਵਿਚ ਖੇਡਾਂ ਨੂੰ ਬੜੇ ਧਿਆਨ ਨਾਲ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ | ਅੱਜ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਲੋਕ ਮੀਡੀਆ, ਖਬਰਾਂ, ਮੈਗਜੀਨਾਂ ਵਿਚ ਖੇਡ ਪੱਤਰਕਾਰ ਦੇ ਰੂਪ ਵਿਚ ਕੰਮ ਕਰਦੇ ਹਨ । ਇਸ ਲਈ ਇਹ ਇਕ ਵਧੀਆ ਕੈਰੀਅਰ ਵਿਕਲਪ ਦੇ ਰੂਪ ਵਿਚ ਆ ਰਿਹਾ ਹੈ । ਖੇਡ ਪੱਤਰਕਾਰ ਨੂੰ ਮਾਸਿਕ ਸੰਚਾਰ (Mass Communication) ਵਿਚ ਡਿਗਰੀ ਦਾ ਡਿਪਲੋਮਾ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਹਨਾਂ ਡਿਗਰੀਆਂ ਵਾਸਤੇ ਖੇਡ ਪੱਤਰਕਾਰ ਨੇ 12ਵੀ ਪਾਸ ਕੀਤੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਉਸ ਕੋਲ ਵੱਖ-ਵੱਖ ਖੇਡ ਦਾ ਖੇਡ ਦੇ ਪ੍ਰਦਰਸ਼ਨ ਦਾ ਗਿਆਨ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਉਸਨੂੰ ਮੀਡੀਆ ਉਤਪਾਦਨ (Production) ਅਤੇ ਪ੍ਰਸਾਰਣ ਬਾਰੇ ਜਾਣਕਾਰੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

3. ਯੋਗਾ ਦੇ ਰੂਪ ਵਿਚ ਕਿੱਤਾ (As a Yoga Instructor) – ਅੱਜ-ਕੱਲ੍ਹ ਹਰ ਕੋਈ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਪ੍ਰਤੀ ਸੁਚੇਤ ਹੋ ਗਿਆ ਹੈ ਅਤੇ ਇਸ ਨੂੰ ਕੈਰੀਅਰ ਦੇ ਰੂਪ ਵਿਚ ਅਪਣਾ ਰਿਹਾ ਹੈ । ਇਸ ਕੈਰੀਅਰ ਵਿਚ ਚੰਗੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਪੈਦਾ ਹੋ ਰਹੀਆਂ ਹਨ ਅਤੇ ਸਮਾਜ ਦੀ ਜ਼ਰੂਰਤ ਨੂੰ ਯੋਗਿਕ ਅਭਿਆਸ ਵੱਲ ਵਧਾਇਆ ਜਾ ਰਿਹਾ ਹੈ । ਇਕ ਯੋਗਾ ਮਾਹਿਰ ਹੋਣ ਲਈ ਵਿਅਕਤੀ ਕੋਲ ਬੈਚਲਰ ਡਿਗਰੀ, ਡਿਪਲੋਮਾ, ਯੋਗ ਵਿਚ ਬੀ.ਐੱਡ. ਦਾ ਸਰਟੀਫਿਕੇਟ ਕੋਰਸ ਹੋਣਾ ਲਾਜ਼ਮੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਵੱਖ-ਵੱਖ ਕੋਰਸਾਂ ਦੀ ਜਾਣਕਾਰੀ ਦਿਓ ।
ਉੱਤਰ-
ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਕੋਰਸਾਂ ਦੇ ਨਾਂ ਹੇਠਾਂ ਦਿੱਤੇ ਗਏ ਹਨ

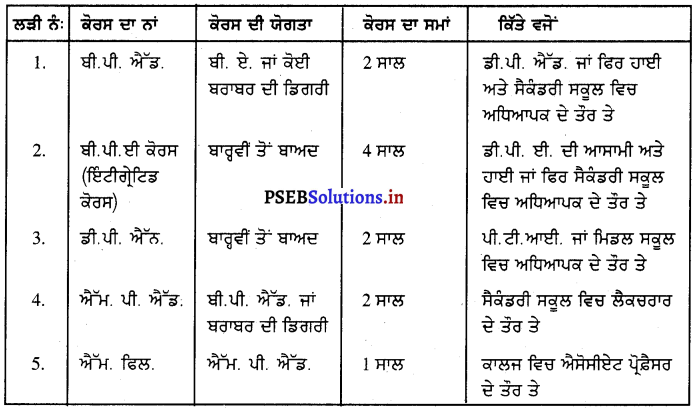
ਪ੍ਰਸ਼ਨ 3.
ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਅਵਾਰਡ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿਉ ।
ਉੱਤਰ-
ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਪੁਰਸਕਾਰ (Rajiv Gandhi Sports Awards) – ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਪੁਰਸਕਾਰ ਸਾਬਕਾ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਰਾਜੀਵ ਗਾਂਧੀ ਦੀ ਯਾਦ ਵਿਚ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਹ ਸਭ ਤੋਂ ਵੱਡੇ ਰੈਂਕ ਦਾ ਰਾਸ਼ਟਰੀ ਪੁਰਸਕਾਰ ਹੈ ਅਤੇ ਇਹ ਖਿਡਾਰੀਆਂ ਦੇ ਮਨੋਬਲ ਅਤੇ ਵਿਸ਼ਵਾਸ ਨੂੰ ਉਤਸਾਹਿਤ ਕਰਨ ਲਈ ਇਹ 1991 ਵਿਚ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ । ਇਹ ਪੁਰਸਕਾਰ ਯੁਵਾ ਮਾਮਲਿਆਂ ਅਤੇ ਖੇਡ ਮੰਤਰਾਲੇ ਦੁਆਰਾ ਖਿਡਾਰੀਆਂ ਨੂੰ ਭਾਰਤ ਵਿਚ ਖੇਡਾਂ ਵਿਚ ਸ਼ਾਨਦਾਰ ਪ੍ਰਦਰਸ਼ਨ ਲਈ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਪੁਰਸਕਾਰ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੇ 7.5 ਲੱਖ ਦਾ ਨਕਦ ਇਨਾਮ, ਅਤੇ ਤਮਗਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਇਹ ਪੁਰਸਕਾਰ ਵਿਸ਼ਵਨਾਥਨ ਆਨੰਦ (Vishwnathan Anand) ਨੇ 1992-1993 ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤਾ ਅਤੇ ਔਰਤਾਂ ਵਿਚ ਕਰਨਮ ਮਲੇਸ਼ਵਰੀ ਨੂੰ ਇਹ ਪੁਰਸਕਾਰ 1995-96 ਵਿਚ ਮਿਲਿਆ | ਪੰਕਜ ਅਡਵਾਨੀ ਇਕ ਅਜਿਹੇ ਪਹਿਲੇ ਖਿਡਾਰੀ ਹੋਏ ਹਨ ਜਿਨ੍ਹਾਂ ਨੂੰ ਦੋ ਖੇਡਾਂ ਸਨੂਕਰ (Snooker) ਅਤੇ ਬਿਲੀਅਰਡਜ਼ (Billiards) ਲਈ ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਰਤਨ ਪੁਰਸਕਾਰ ਮਿਲਿਆ ਹੈ ।

ਰਾਜੀਵ ਗਾਂਧੀ ਖੇਡ ਪੁਰਸਕਾਰ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਨਿਯਮ (Rules to get Rajiv Gandhi Sports Award) – ਭਾਰਤ ਸਰਕਾਰ ਸੰਬੰਧਿਤ ਖੇਡ ਫੈਡਰੇਸ਼ਨਾਂ ਤੋਂ ਖਿਡਾਰੀ ਦੇ ਨਾਮ ਦੀ ਸੂਚੀ ਮੰਗਵਾਉਂਦੀ ਹੈ, ਜਿਸ ਦੀ ਆਖਰੀ ਮਿਤੀ 31 ਮਈ ਹੁੰਦੀ ਹੈ । ਇੱਥੇ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਦੀ ਨਾਮਜ਼ਦਗੀ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਜਿਨ੍ਹਾਂ ਨੇ ਓਲੰਪਿਕ, ਕਾਮਨਵੈਲਥ ਗੇਮਜ਼, ਏਸ਼ੀਅਨ ਖੇਡਾਂ ਵਿਚ ਮੈਡਲ ਪ੍ਰਾਪਤ ਕੀਤੇ ਹੁੰਦੇ ਹਨ ।

2018 ਵਿਚ ਰਾਜੀਵ ਗਾਂਧੀ ਪੁਰਸਕਾਰ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੇ ਖਿਡਾਰੀ-

ਖਿਡਾਰੀ ਦਾ ਨਾਮ	ਖੇਡ
1. ਮੀਰਾਬਾਈ ਚਾਨੂੰ	ਵੇਟ ਲੇਟਟਿੰਗ
2. ਵਿਰਾਟ ਕੋਹਲੀ	ਕ੍ਰਿਕਟ

ਪ੍ਰਸ਼ਨ 4.
ਭਾਰਤ ਵਿਚ ਖਿਡਾਰੀ ਨੂੰ ਦਿੱਤੇ ਜਾਣ ਵਾਲੇ ਸਰਵੋਤਮ ਅਵਾਰਡ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਅਰਜਨ ਐਵਾਰਡ (Arjuna Award) – ਇਹ ਪੁਰਸਕਾਰ 1961 ਵਿਚ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ ਸੀ । ਇਹ ਖਿਡਾਰੀਆਂ ਨੂੰ ਦਿੱਤਾ ਜਾਣ ਵਾਲਾ ਸਭ ਤੋਂ ਵੱਡਾ ਇਨਾਮ ਹੈ ਅਤੇ ਇਹ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੇ ਲਗਾਤਾਰ ਚਾਰ ਸਾਲ ਤਕ ਕੌਮੀ ਅਤੇ ਅੰਤਰਰਾਸ਼ਟਰੀ ਪੱਧਰ ਜਿਵੇਂ ਕਿ ਓਲੰਪਿਕ ਖੇਡਾਂ, ਏਸ਼ੀਅਨ ਖੇਡਾਂ, ਕਾਮਨਵੈਲਥ ਅਤੇ ਰਾਸ਼ਟਰੀ ਪੱਧਰ ਤੇ ਬੇਹਤਰੀਨ ਪ੍ਰਦਰਸ਼ਨ ਕੀਤਾ ਹੋਏ । ਇਸ ਅਵਾਰਡ ਦੇ ਤਹਿਤ ਇਕ ਫੀ (ਅਰਜਨ ਦਾ ਕਾਂਸੀ ਦਾ ਬੁੱਤ) ਅਤੇ 5 ਲੱਖ ਰੁਪਏ ਨਕਦ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ ।

ਇਹ ਅਵਾਰਡ ਖੇਡ ਮੰਤਰਾਲੇ ਵਜੋਂ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ 1961 ਵਿਚ ਸਭ ਤੋਂ ਪਹਿਲਾਂ 6 ਖਿਡਾਰੀਆਂ ਨੂੰ ਇਹ ਅਵਾਰਡ ਦਿੱਤਾ ਗਿਆ । ਇਹ ਖਿਡਾਰੀ ਸਲੀਮ ਦੂਰਾਨੀ (Saleem Durrani) ਕ੍ਰਿਕਟ, ਗੁਰਬਚਨ ਸਿੰਘ ਰੰਧਾਵਾ (Gurbachan Singh Randhawa) ਐਥਲੈਟਿਕਸ, ਸਰਬਜੀਤ ਸਿੰਘ (Sarabjit Singh) ਬਾਸਕੇਟਬਾਲ, ਮੈਨੁਅਲ ਮੋਰਾਨ (Manuel Aaron) ਸ਼ਤਰੰਜ, ਨੰਦੁ ਨਾਟੇਕਰ (Nandhu Natekar) ਬੈਡਮਿੰਟਨ ਅਤੇ ਐਲ. ਬੀ. ਡਿਸੂਜਾ (LB D’Souza) ਬਾਕਸਿੰਗ ਮੀਨਾ ਸ਼ਾਹ (Meena Shah) ਬੈਡਮਿੰਟਨ ਪਹਿਲੀ ਮਹਿਲਾ ਸੀ ਜਿਸ ਨੂੰ 1962 ਵਿਚ ਇਹ ਅਵਾਰਡ ਦਿੱਤਾ ਗਿਆ |

ਅਰਜੁਨ ਅਵਾਰਡ ਦੇ ਨਿਯਮ-ਅਰਜੁਨ ਅਵਾਰਡ ਦੇ ਨਿਯਮ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ :-

1. ਅਰਜੁਨ ਪੁਰਸਕਾਰ ਦਾ ਉਦੇਸ਼ ਭਾਰਤ ਵਿਚ ਖੇਡਾਂ ਦੇ ਵਿਕਸਿਤ ਮਿਆਰਾਂ ਨੂੰ ਵਿਕਸਿਤ ਕਰਨਾ ਹੈ ।
2. ਭਾਰਤ ਸਰਕਾਰ ਹਰ ਸਾਲ ਮਿੱਥੇ ਸਮੇਂ ਤੇ ਖਿਡਾਰੀਆਂ ਦੇ ਨਾਮ ਸੂਚੀ ਫੈਡਰੇਸ਼ਨ ਤੋਂ ਮੰਗ ਲੈਂਦੀ ਹੈ ।
3. ਆਮ ਤੌਰ ਦੇ ਹਰੇਕ ਸਾਲ ਹਰੇਕ ਈਵੇਂਟ ਲਈ ਇਕ ਖਿਡਾਰੀ ਨੂੰ ਅਵਾਰਡ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸੇ ਈਵੈਂਟ ਵਿਚ ਨਿਰਵਿਵਾਦ ਔਰਤ ਨੂੰ ਦੂਜਾ ਇਨਾਮ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
4. ਨਾਮਜ਼ਦਗੀਆਂ ਦੀ ਸੂਚੀ ਨਿਰਧਾਰਿਤ ਸਮੇਂ ਵਿਚ ਖੇਡ ਵਿਭਾਗ ਨੂੰ ਜਮਾਂ ਕਰਵਾ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
5. ਨਾਮਜ਼ਦਗੀਆਂ ਦਾਖਲ ਕਰਨ ਲਈ ਨਿਸਚਿਤ ਮਿੱਤੀ ਸਿਰਫ ਕੇਂਦਰ ਸਰਕਾਰ ਵਲੋਂ ਵਧਾਈ ਜਾ ਸਕਦੀ ਹੈ ।
6. ਸਰਕਾਰ ਵਲੋਂ ਇਕ ਕਮੇਟੀ ਦਾ ਗਠਨ ਹੁੰਦਾ ਹੈ ਜੋ ਕਿ ਫੈਡਰੇਸ਼ਨਾਂ ਵਲੋਂ ਦਿੱਤੇ ਨਾਮਾਂ ਦੀ ਪੜਤਾਲ ਕਰਦੀ ਹੈ ।
7. ਜੇਕਰ ਸਰਕਾਰ ਫੈਡਰੇਸ਼ਨ ਤੋਂ ਕੋਈ ਸੂਚੀ ਪ੍ਰਾਪਤ ਨਹੀਂ ਕਰਦੀ ਤਾਂ ਭਾਰਤ ਸਰਕਾਰ ਖੁਦ ਹੀ ਸਰਵੋਤਮ ਖਿਡਾਰੀ ਨੂੰ ਪੁਰਸਕਾਰ ਦੇ ਸਕਦੀ ਹੈ ।
8. ਖੇਡ ਫੈਡਰੇਸ਼ਨਾਂ ਤਿੰਨ ਖਿਡਾਰੀਆਂ ਦਾ ਨਾਮ ਭਾਰਤ ਸਰਕਾਰ ਨੂੰ ਭੇਜਦੀ ਹੈ ਜਿਸ ਵਿਚ ਇਕ ਸਰਵੋਤਮ . ਖਿਡਾਰੀ ਦੇ ਰੂਪ ਵਿਚ ਚੁਣ ਲਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਦੂਜਾ ਨਾਮ ਮਹਿਲਾ ਖਿਡਾਰੀ ਦਾ ਹੋ ਸਕਦਾ ਹੈ ।
9. ਅਵਾਰਡ ਪੇਸ਼ਕਾਰੀ ਮਿਤੀ ਸਰਕਾਰ ਵਲੋਂ ਤੈਅ ਕੀਤੀ ਜਾਂਦੀ ਹੈ। ।
10. ਇਕ ਖਿਡਾਰੀ ਨੂੰ ਦੋ ਵਾਰ ਪੁਰਸਕਾਰ ਨਹੀਂ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ।
11. ਇਹ ਅਵਾਰਡ ਮਰਨ ਉਪਰੰਤ ਵੀ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
12. ਅਵਾਰਡ ਨਿਯਮਾਂ ਵਿਚ ਭਾਰਤ ਸਰਕਾਰ ਦਾ ਫੈਸਲਾ ਵੀ ਆਖਰੀ ਫੈਸਲਾ ਹੁੰਦਾ ਹੈ । ਅਗਰ ਕਿਸੇ ਕਾਰਨ ਕਰਕੇ ਅਵਾਰਡ ਵਾਪਿਸ ਲੈਣਾ ਹੋਵੇ ਤਾਂ ਖਿਡਾਰੀ ਉਸੇ ਹਾਲਤ ਵਿਚ ਵਾਪਿਸ ਕਰਦਾ ਹੈ ਇਸ ਵਿਚ ਗ੍ਰਹਿਣ ਕੀਤਾ ਸੀ ।
13. ਅਰਜਨ ਅਵਾਰਡ ਦੇ ਨਿਯਮ 1996 ਵਿਚ ਬਣਾਏ ਗਏ ਸਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਸਕੂਲ ਅਤੇ ਕਾਲਜ ਅਧਿਆਪਕ ਬਣਨ ਲਈ ਕਿਹੜੇ ਕੋਰਸ ਜ਼ਰੂਰੀ ਹਨ ਅਤੇ ਉਹਨਾਂ ਦੀ ਦਾਖਲੇ ਵਾਸਤੇ ਯੋਗਤਾ ਕੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਸਕੂਲ ਅਤੇ ਕਾਲਜ ਦੇ ਅਧਿਆਪਕਾਂ ਵਾਸਤੇ ਜ਼ਰੂਰੀ ਕੋਰਸ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ :
1. ਡੀ. ਪੀ. ਐੱਡ. – ਇਹ ਕੋਰਸ ਪਹਿਲਾਂ ਸੀ.ਪੀ. ਐੱਡ. ਦੇ ਨਾਮ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਸੀ ਅਤੇ ਬਾਅਦ ਵਿਚ ਇਸ ਨੂੰ ਡੀ.ਪੀ.ਐੱਡ. ਕਿਹਾ ਜਾਣ ਲੱਗ ਪਿਆ । ਇਸਦੇ ਨਾਲ ਹੀ ਇਸ ਦੀ ਮਿਆਦ ਇਕ ਸਾਲ ਤੋਂ ਵਧਾ ਕੇ ਦੋ ਸਾਲ ਕਰ ਦਿੱਤੀ ਗਈ ਸੀ । ਇਸ ਕੋਰਸ ਨੂੰ ਪੂਰਾ ਕਰਕੇ ਵਿਅਕਤੀ ਕਿਸੇ ਵੀ ਐਲੀਮੈਂਟਰੀ ਸਕੂਲ ਪੀ.ਟੀ.ਆਈ. ਦੇ ਤੌਰ ‘ਤੇ · ਅਧਿਆਪਕ ਵਜੋਂ ਕੰਮ ਕਰ ਸਕਦਾ ਹੈ ।

ਡੀ.ਪੀ.ਐੱਡ. ਵਿਚ ਦਾਖ਼ਲੇ ਲਈ ਯੋਗਤਾ-
(ਉ) ਵਿਅਕਤੀ ਨੇ ਕਿਸੇ ਵੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਬੋਰਡ ਤੋਂ ਬਾਰਵੀਂ 50% ਅੰਕਾਂ ਨਾਲ ਪਾਸ ਕੀਤੀ ਹੋਵੇ ।
(ਅ) ਉਹ ਫਿਜੀਕਲ ਤੌਰ ‘ਤੇ ਤੰਦਰੁਸਤ ਹੋਵੇ ।
(ਇ) , ਉਸ ਨੇ ਦਾਖ਼ਲੇ ਵਾਸਤੇ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਦਾ ਟੈਸਟ ਪਾਸ ਕੀਤਾ ਹੋਵੇ ।

2. ਬੀ. ਪੀ. ਐੱਡ. (ਇੰ ਟਿਡ ਕੋਰਸ) – ਇਹ ਕੋਰਸ ਚਾਰ ਸਾਲ ਦੀ ਮਿਆਦ ਵਾਲਾ ਹੈ ਅਤੇ ਕਈ ਕਾਲਜਾਂ ਅਤੇ ਯੂਨੀਵਰਸਿਟੀ ਵਲੋਂ ਕਰਵਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਵੀ ਬੈਚਲਰ ਆਫ ਆਰਟਸ ਦੇ ਬਰਾਬਰ ਦੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਡਿਗਰੀ ਹੁੰਦੀ ਹੈ । ਪਹਿਲਾਂ ਇਸ ਕੋਰਸ ਦੀ ਮਿਆਦ ਤਿੰਨ ਸਾਲ ਦੀ ਰੱਖੀ ਗਈ ਪਰ ਐੱਨ. ਸੀ. ਆਰ. ਟੀ. ਸੀ. ਨੇ 2016-17
ਵਿਚ ਇਸ ਦੀ ਮਿਆਦ ਬਦਲ ਕੇ ਚਾਰ ਸਾਲ ਕਰ ਦਿੱਤੀ ਗਈ ਹੈ । ਚਾਰ ਸਾਲ ਪੂਰੇ ਹੋਣ ਤੋਂ ਬਾਅਦ ਵਿਅਕਤੀ ਸਿੱਧੇ | ਤੌਰ `ਤੇ ਐੱਮ.ਪੀ.ਐੱਡ. ਵਿਚ ਦਾਖਲਾ ਲੈ ਸਕਦਾ ਹੈ । ਬੀ.ਪੀ. ਐੱਡ. ਦੀ ਡਿਗਰੀ ਪੂਰੀ ਕਰਨ ਤੋਂ ਬਾਅਦ ਵਿਅਕਤੀ ਕਿਸੇ ਵੀ ਸਕੂਲ ਵਿਚ ਪੀ.ਟੀ.ਆਈ. ਕੰਮ ਕਰ ਸਕਦਾ ਹੈ ।
ਬੀ. ਪੀ. ਐੱਡ. ਲਈ ਯੋਗਤਾ
(ਉ) ਕਿਸੇ ਵੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਬੋਰਡ ਤੋਂ ਬਾਰਵੀਂ 50% ਅੰਕਾਂ ਨਾਲ ਪਾਸ ਕੀਤੀ ਹੋਵੇ ।
(ਅ) ਦਾਖ਼ਲੇ ਵਾਸਤੇ ਇਨਟਰੈਨਸ ਪੇਪਰ ਅਤੇ ਫਿਜ਼ੀਕਲ ਟੈਸਟ ਪਾਸ ਕੀਤਾ ਹੋਵੇ ।
(ਈ) ਵਿਅਕਤੀ ਕਿਸੇ ਖੇਡ ਵਿਚ ਮਾਹਿਰ ਜ਼ਰੂਰ ਹੋਵੇ ।
(ਸ) ਡੀ.ਪੀ.ਐੱਡ. ਡਿਗਰੀ 50% ਅੰਕਾਂ ਨਾਲ ਪਾਸ ਹੋਵੇ ।

3. ਬੀ. ਪੀ. ਐੱਡ. ਡਿਪਲੋਮਾ (2 ਸਾਲ) – ਇਹ ਦੋ ਸਾਲ ਦੀ ਮਿਆਦ ਵਾਲਾ ਕੋਰਸ ਹੈ ਅਤੇ ਗੈਜੂਏਸ਼ਨ ਦੀ ਬਰਾਬਰ ਦੀ ਡਿਗਰੀ ਤੋਂ ਬਾਅਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਡਿਪਲੋਮੇ ਨੂੰ ਕਈ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਕਾਲਜ ਅਤੇ ਯੂਨੀਵਰਸਿਟੀ ਵਿਚ ਕਰਵਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਡਿਪਲੋਮੇ ਵਿਚ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਪਿਛੋਕੜ ਕਈ ਮੈਡੀਕਲ ਵਿਸ਼ਿਆਂ ਅਤੇ ਸਿੱਖਿਆ ਦੇਣ ਦੇ ਕਈ ਤਰੀਕੇ ਅਤੇ ਹੋਰਨਾਂ ਖੇਡਾਂ ਦੀ ਜਾਣਕਾਰੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਡਿਪਲੋਮੇ ਨੂੰ ਪੂਰਾ ਕਰਨ ਤੋਂ ਬਾਅਦ ਵਿਅਕਤੀ ਕਿਸੇ ਹਾਈ ਜਾਂ ਸੈਕੰਡਰੀ ਸਕੂਲ ਵਿਚ ਬਤੌਰ ਅਧਿਆਪਕ ਪੜ੍ਹਾਉਣ ਦੇ ਕਾਬਿਲ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਬੀ. ਪੀ. ਐੱਡ. ਡਿਪਲੋਮੇ ਲਈ ਯੋਗਤਾ-
(ਉ) ਕਿਸੇ ਵੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਯੂਨੀਵਰਸਿਟੀ ਤੋਂ 50% ਅੰਕਾਂ ਨਾਲ ਗੇਜਏਸ਼ਨ ਪਾਸ ਕੀਤੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ।
(ਅ) ਖਿਡਾਰੀ ਦਾ ਨੈਸ਼ਨਲ ਜਾਂ ਅੰਤਰ-ਯੂਨੀਵਰਸਿਟੀ ਜਾਂ ਫਿਰ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਪੱਧਰ ਤੇ ਕਿਸੇ ਇਕ ਖੇਡ ਵਿਚ ਭਾਗ ਲਿਆ ਜਾਂ ਫਿਰ ਮੈਡਲ ਜ਼ਰੂਰ ਪ੍ਰਾਪਤ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
(ਈ) ਸਰੀਰਕ ਯੋਗਤਾ ਦਾ ਟੈਸਟ ਪਾਸ ਕਰਨਾ ਲਾਜ਼ਮੀ ਹੈ ।

4. ਐੱਮ. ਪੀ. ਐੱਡ. – ਇਹ ਦੋ ਸਾਲ ਦੀ ਮਿਆਦ ਦਾ ਕੋਰਸ ਹੈ ਅਤੇ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਕਾਲਜਾਂ ਅਤੇ ਯੂਨੀਵਰਸਿਟੀਆਂ ਦੁਆਰਾ ਕਰਵਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਇਕ ਮਾਸਟਰ ਡਿਗਰੀ ਹੈ ਜਿਸ ਨੂੰ ਕਰਨ ਤੋਂ ਬਾਅਦ ਵਿਅਕਤੀ ਕਿਸੇ ਵੀ ਹਾਈ ਸੈਕੰਡਰੀ ਵਿਚ ਬਤੌਰ ਲੈਕਚਰਾਰ ਅਧਿਆਪਕ ਵਜੋਂ ਕੰਮ ਕਰ ਸਕਦਾ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਉਹ ਯੂ. ਸੀ. ਨੈੱਟ ਅਤੇ ਪੀ. ਐੱਚ. ਡੀ. ਕਰਕੇ ਕਾਲਜਾਂ ਵਿਚ ਇਸੀਟੈਟ ਪ੍ਰੋਫੈਸਰ ਵੀ ਲੱਗ ਸਕਦਾ ਹੈ ।
ਐੱਮ. ਪੀ. ਐੱਡ. ਲਈ ਯੋਗਤਾ-
(ਉ) ਇਹ ਕੋਰਸ ਵਿਚ ਦਾਖ਼ਲੇ ਵਾਸਤੇ ਬੀ.ਪੀ.ਐੱਡ. (2 ਸਾਲ) ਦਾ ਬੀ.ਪੀ.ਐੱਡ. (ਇੰਟੀਗ੍ਰਡ) ਕੋਰਸ 50% ਅੰਕਾਂ ਨਾਲ ਪਾਸ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
(ਅ) ਖਿਡਾਰੀ ਕਿਸੇ ਖੇਡ ਦਾ ਮਾਹਿਰ ਅਤੇ ਕਿਸੇ ਵੀ ਪੱਧਰ ਤੇ ਖੇਡਿਆ ਹੋਵੇ ।
(ਇ) ਸਰੀਰਕ ਯੋਗਤਾ ਦਾ ਟੈਸਟ ਪਾਸ ਕੀਤਾ ਹੋਵੇ ।

5. ਐੱਮ. ਫਿਲ. (ਮਾਸਟਰ ਆਫ ਫਿਲਾਸਫੀ)-ਇਹ ਇਕ ਖੋਜ ਨਾਲ ਜੁੜਿਆ ਖੇਤਰ ਹੈ ਜਿਸ ਵਿਚ ਵਿਅਕਤੀ ਆਪਣੀ ਰੁਚੀ ਦੇ ਹਿਸਾਬ ਨਾਲ ਖੋਜ ਕਰਨਾ ਅਤੇ ਉਸਦੇ ਤਰੀਕਿਆਂ ਦਾ ਅਧਿਐਨ ਕਰਦੇ ਹਨ ।
ਯੋਗਤਾ-

1. ਵਿਅਕਤੀ ਨੇ ਐੱਮ.ਪੀ.ਐੱਡ. ਜਾਂ ਮਾਸਟਰ ਡਿਗਰੀ ਘੱਟੋ-ਘੱਟ 55% ਪਾਸ ਕੀਤੀ ਹੋਵੇ ।
2. ਵਿਅਕਤੀ ਨੇ ਪ੍ਰਵੇਸ਼ ਪ੍ਰੀਖਿਆ ਪਾਸ ਕੀਤੀ ਹੋਣੀ ਲਾਜ਼ਮੀ ਹੈ ।

6. ਪੀ-ਐੱਚ. ਡੀ. (ਡਾਕਟਰ ਆਫ ਫਿਲਾਸਫੀ) – ਇਹ ਸਭ ਤੋਂ ਉੱਚੀ ਡਿਗਰੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਦੀ ਮਿਆਦ 3 ਸਾਲ ਤੋਂ 4 ਸਾਲ ਤੱਕ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਵਿਅਕਤੀ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਕਿਸੇ ਵੀ ਵਿਸ਼ੇ ਤੇ ਆਪਣੀ ਰੁਚੀ ਮੁਤਾਬਿਕ ਨਵੀਂ ਖੋਜ ਕਰਦਾ ਹੈ ਅਤੇ ਜੋ ਨਤੀਜੇ ਆਉਂਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਸਰੀਰਕ ਸਿੱਖਿਆ ਦੇ ਵਿਕਾਸ ਵਿਚ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਡਿਗਰੀ ਨੂੰ ਪੂਰਾ ਕਰਨ ਤੋਂ ਵਿਅਕਤੀ ਨੂੰ ਡਾਕਟਰ ਦੀ ਉਪਾਧੀ ਨਾਲ ਨਿਵਾਜਿਆ ਜਾਂਦਾ ਹੈ ।
ਯੋਗਤਾ-

1. ਇਸ ਵਿਚ ਪ੍ਰਵੇਸ਼ ਪ੍ਰੀਖਿਆ ਪਾਸ ਕਰਨੀ ਜ਼ਰੂਰੀ ਹੁੰਦੀ ਹੈ ਜੇਕਰ ਵਿਅਕਤੀ ਨੇ ਯੂ.ਜੀ.ਸੀ. ਨੈੱਟ ਨਹੀਂ ਪਾਸ ਕੀਤਾ ।
2. ਐੱਮ.ਪੀ.ਐੱਡ. ਮਾਸਟਰ ਡਿਗਰੀ ਅਤੇ ਐੱਮ. ਫਿਲ ਤੋਂ ਬਾਅਦ ਇਸ ਨੂੰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

7. ਯੋਗ ਮਾਹਿਰ-ਅੱਜ-ਕੱਲ੍ਹ ਹਰ ਕੋਈ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਪ੍ਰਤੀ ਸੁਚੇਤ ਹੋ ਗਿਆ ਹੈ ਅਤੇ ਇਸ ਨੂੰ ਕਿੱਤੇ ਵਜੋਂ ਅਪਣਾਉਣਾ ਚਾਹੁੰਦੇ ਹਨ । ਯੋਗ ਮਾਹਿਰ ਕੋਲ ਹੇਠ ਲਿਖਿਆਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਡਿਗਰੀ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ :-

1. ਸਰਟੀਫਿਕੇਟ ਇੰਨ ਯੋਗਾ-ਇਸ ਕੋਰਸ ਨੂੰ ਕਰਨ ਵਾਸਤੇ ਘੱਟੋ-ਘੱਟ ਬਾਰਵੀਂ ਪਾਸ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਇਹ ਛੇ ਹਫ਼ਤਿਆਂ ਦੀ ਮਿਆਦ ਵਾਲਾ ਕੋਰਸ ਹੁੰਦਾ ਹੈ ਜਿਸ ਵਿਚ ਯੋਗਾ ਦੇ ਆਸਨਾਂ ਦਾ ਗਿਆਨ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
2. ਬੈਚਲਰ ਆਫ਼ ਯੋਗਾ-ਇਹ ਤਿੰਨ ਸਾਲ ਦੀ ਮਿਆਦ ਦੀ ਡਿਗਰੀ ਹੈ ਅਤੇ ਗੈਜੂਏਸ਼ਨ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਦਾਖ਼ਲਾ ਲੈਣ ਲਈ ਬਾਰੂਵੀ ਪਾਸ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ।
3. ਡਿਪਲੋਮਾ ਇੰਨ ਯੋਗਾ-ਇਹ ਇਕ ਸਾਲ ਦੀ ਮਿਆਦ ਵਾਲਾ ਕੋਰਸ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਹ ਬੈਚਲਰ ਡਿਗਰੀ ਤੋਂ ਬਾਅਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
4. ਐੱਮ. ਐੱਸ. ਸੀ. ਇੰਨ ਯੋਗਾ-ਇਹ ਦੋ ਸਾਲ ਦੀ ਮਿਆਦ ਦਾ ਕੋਰਸ ਹੈ ਅਤੇ ਇਸ ਵਿਚ ਦਾਖ਼ਲੇ ਵਾਸਤੇ ਵਿਅਕਤੀ ਕੋਲ ਗੈਜੂਏਸ਼ਨ ਜਾਂ ਬੈਚਲਰ ਡਿਗਰੀ ਕੀਤੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਇਹਨਾਂ ਉਪਰੋਕਤ ਕੋਰਸਾਂ ਨੂੰ ਕਈ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਕਾਲਜ ਅਤੇ ਯੂਨੀਵਰਸਿਟੀਆਂ ਕਰਵਾਉਂਦੀਆਂ ਹਨ ।

8. ਮਾਸਟਰ ਡਿਗਰੀ ਇਨ-ਸਪੋਰਟਸ ਕੋਚਿੰਗ (Master Degree in Sports Coaching) – ਇਹ ਦੋ ਸਾਲ ਦੀ ਮਿਆਦ ਵਾਲੀ ਡਿਗਰੀ ਹੈ ਜਿਸ ਵਿਚ ਕੋਚਾਂ ਵਿਚ ਰਿਸਰਚ ਵਿਵਹਾਰ ਦਾ ਵਿਕਾਸ ਕਰਨਾ ਹੈ । ਇਹ ਡਿਗਰੀ ਐਥਲੈਟਿਕਸ, ਬਾਸਕੇਟਬਾਲ, ਫੁੱਟਬਾਲ, ਹਾਕੀ, ਸਵੀਮਿੰਗ, ਵਾਲੀਬਾਲ, ਵੇਟ ਲਿਫਟਿੰਗ ਅਤੇ ਕੁਸ਼ਤੀ ਲਈ ਮੌਜੂਦ ਹੈ। ਅਤੇ ਇਹ ਪੰਜਾਬੀ ਯੂਨੀਵਰਸਿਟੀ ਪਟਿਆਲਾ ਤੋਂ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੈ । ਇਸ ਡਿਗਰੀ ਵਾਸਤੇ ਵਿਅਕਤੀ ਗੈਜੂਏਟ ਅਤੇ ਐੱਸ.ਏ.ਆਈ. (SAI) ਜਾਂ ਐੱਨ.ਐੱਸ.ਐੱਨ.ਆਈ.ਐੱਸ. (NSNIS) ਤੋਂ 60% ਨਾਲ ਡਿਪਲੋਮਾ ਪਾਸ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

9. ਪੋਸਟ ਗ੍ਰੈਜੂਏਟ ਡਿਪਲੋਮਾ ਇਨ ਸਪੋਰਟਸ ਮੈਡੀਸਨ (Post Graduate Diploma in Sports Medicine) – ਇਹ ਡਿਗਰੀ ਦਾ ਐੱਮ.ਬੀ.ਬੀ.ਐੱਸ. (MBBS) ਦੇ ਡਾਕਟਰਾਂ ਵਾਸਤੇ ਆਯੋਜਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਡਿਗਰੀ ਵਾਸਤੇ ਗੈਜੂਏਟ ਡਿਗਰੀ ਜਾਂ ਮੈਡੀਕਲ ਤੋਂ ਕੀਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਦੀ ਮਿਆਦ ਦੋ ਸਾਲ ਦੀ ਹੈ । ਇਹ ਬਾਬਾ ਫ਼ਰੀਦ ਯੂਨੀਵਰਸਿਟੀ ਆਫ਼ ਸਾਇੰਸਜ਼ ਨਾਲ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੈ ।

10. ਸਰਟੀਫਿਕੇਟ ਕੋਰਸ ਇਨ ਸਪੋਰਟਸ ਕੋਚਿੰਗ (Certificate Course in Sports Coaching) – ਇਹ ਛੇ ਹਫਤਿਆਂ ਦਾ ਸਰਟੀਫਿਕੇਟ ਕੋਰਸ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸ ਵਿਚ ਸਕੂਲ, ਕਾਲਜਾਂ, ਯੂਨੀਵਰਸਿਟੀ ਜਾਂ ਕਿਸੇ ਵੀ ਸਪੋਰਟਸ ਏਜੰਸੀ ਦੇ ਅਧਿਆਪਕ ਜਾਂ ਕੋਚ ਇਸ ਨੂੰ ਕਰ ਸਕਦੇ ਹਨ ।

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.6

Direction (1 – 4): Examine the consistency of the following system of equations.

Question 1.
x + 2y = 2, 2x + 3y = 3.
Solution.
The given system of equations is
x + 2y = 2
2x + 3y = 3
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{ll}
1 & 2 \\
2 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\)

Now, |A| = 1(3) – 2(2) = 3 – 4 = – 1 ≠ 0
So, A is non-singular. Therefore, A^-1 exists.
Hence, the given system of equations is consistent.

Question 2.
2x – y = 5, x + y = 4.
Solution.
The given system of equations is
2x – y = 5
x + y = 4
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{cc}
2 & -1 \\
1 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
5 \\
4
\end{array}\right]\)
Now, |A| = 2(1) – (- 1) = 2 + 1 = 3 ≠ 0.
So, A is non-singular. Therefore, A^-1 exists.
Hence, the given system of equations is consistent.

Question 3.
x + 3y = 5, 2x + 6y = 8
Solution.
The given system of equations is
x + 3y = 5
2x + 6y = 8
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 6
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
5 \\
8
\end{array}\right]\).
Now, |A| = 1(6) – 3(2) = 6 – 6 = 0
So, A is a singular matrix.
Now, (adj A) = \(\left[\begin{array}{rr}
6 & -3 \\
-2 & 1
\end{array}\right]\)
(adj A) B = \(\left[\begin{array}{cc}
6 & -3 \\
-2 & 1
\end{array}\right]\left[\begin{array}{l}
5 \\
8
\end{array}\right]\)
= \(\left[\begin{array}{c}
30-24 \\
-10+8
\end{array}\right]=\left[\begin{array}{c}
6 \\
-2
\end{array}\right]\) ≠ 0.
Thus, the solution of given system of equations does not exist.
Hence, tne system or equations is inconsistent.

Question 4.
x + y + z = 1, 2x + 3y + 2z = 2, ax + ay + 2az = 4.
Solution.
The given system of equations is
x + y + z = 1
2x + 63y + 2z = 2
czx + ay + 2az = 4
This system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
2 & 3 & 2 \\
a & a & 2 a
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
2 \\
4
\end{array}\right]\)
Now, |A| = 1(6a – 2a) – 1 (4a – 2a) + 1 (2a – 3a)
= 4a – 2a – a
= 4a – 3a = a ≠ 0.
So, A is non-singular. Therefore, A^-1 exists.
Hence, the given system of equations is consistent.

Question 5.
3x – y – 2z = 2, 2y – z = – 1, 3x – 5y = 3.
Solution.
The given system of equations is
3x – y – 2z = 2
2y – z = – 1
3x – 5y = 3
This system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{ccc}
3 & -1 & -2 \\
0 & 2 & -1 \\
3 & -5 & 0
\end{array}\right]\), X = \(=\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
2 \\
-1 \\
3
\end{array}\right]\)
Now, |A| = 3(0 – 5) – 0 + 3(1 + 4)
= – 15 + 15 = 0
So, A is a singular matrix.
Now, (adj A ) = \(\left[\begin{array}{ccc}
-5 & 10 & 5 \\
-3 & 6 & 3 \\
-6 & 12 & 6
\end{array}\right]\)

(adj A) B = \(\left[\begin{array}{ccc}
-5 & 10 & 5 \\
-3 & 6 & 3 \\
-6 & 12 & 6
\end{array}\right]\left[\begin{array}{r}
2 \\
-1 \\
3
\end{array}\right]\)

= \(\left[\begin{array}{c}
-10-10+15 \\
-6-6+9 \\
-12-12+18
\end{array}\right]=\left[\begin{array}{c}
-5 \\
-3 \\
-6
\end{array}\right] \neq 0\)

Thus, the solution of the given system of equations does not exist.
Hence, the system of the equations is inconsistent.

Question 6.
5x – y + 4z = 5, 2x + 3y + 5z = 2, 5x – 2y + 6z = – 1.
Solution.
The given system of equations is
5x – y + 4z = 5
2x + 3y + 5z =2
5x – 2y + 6z = – 1
This system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{rrr}
5 & -1 & 4 \\
2 & 3 & 5 \\
5 & -2 & 6
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
5 \\
2 \\
-1
\end{array}\right]\)
5 -2 6 z -1
Now, |A| = 5(18 + 10) + 1 (12 – 25) + 4(- 4 – 15)
= 5 (28) + 1 (- 13) + 4 (- 19)
= 140 – 13 – 76 = 51 ≠ 0
So, A is non-singular. Therefore, A’ exists.
Hence, the given system of equations is consistent.

Direction (7 – 14): Solve the system of linear equations, using matrix method.

Question 7.
5x + 2y = 4, 7x + 3y = 5.
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{ll}
5 & 2 \\
7 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
4 \\
5
\end{array}\right]\)
Now, |A| = 15 – 14 = 1 ≠ 0.
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 3,
A₁₂ = – 7,
A₂₁ = – 2,
A₂₂ = 5

Question 8.
2x – y = – 2, 3x + 4y = 3
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{rr}
2 & -1 \\
3 & 4
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{r}
-2 \\
3
\end{array}\right]\).
Now, |A| = 8 + 3 = 11 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 4,
A₁₂ = – 3,
A₂₁ = 1,
A₂₂ = 2

Question 9.
4x – 3y = 3, 3x – 5y = 7.
Solution.
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{cc}
4 & -3 \\
3 & -5
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
3 \\
7
\end{array}\right]\)
Now, |A| = – 20 + 9 = – 11 ≠ 0.
Thus, A is non-singular. Therefore, its inverse exists.
Determinants 179
Cofactors of A are
A₁₁ = – 5,
A₁₂ = – 3,
A₂₁ = 3,
A₂₂ = 4

Question 10.
5x + 2y = 3, 3x + 2y = 5.
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{ll}
5 & 2 \\
3 & 2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\).
Now, |A| = 10 – 6 = 4 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 2,
A₁₂ = – 3,
A₂₁ = – 2,
A₂₂ = 5

Question 11.
2x + y + z = 1, x – 2y – z = \(\frac{3}{2}\), 3y – 5z = 9.
Solution.
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{rrr}
2 & 1 & 1 \\
1 & -2 & -1 \\
0 & 3 & -5
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
\frac{3}{2} \\
9
\end{array}\right]\)

Now, |A| = 2(10 + 3) – 1 (- 5 – 3) + 0
= 2 (13) – 1 (- 8) = 26 + 8 = 34 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 13,
A₁₂ = 5,
A₁₃ = 3
A₂₁ = 8,
A₂₂ = – 10,
A₂₃ = – 6
A₃₁ = 1,
A₃₂ = 3,
A₃₃ = – 5

Question 12.
x – y + z = 4, 2x + y – 3z = 0, x + y + z = 2.
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
2 & 1 & -3 \\
1 & 1 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
4 \\
0 \\
2
\end{array}\right]\)
Now |A| = 1 (1 + 3) + 1 (2 + 3) + 1 (2 – 1)
= 4 + 5 + 1 = 10 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 4,
A₁₂ = – 5,
A₁₃ = 1
A₂₁ = 2,
A₂₂ = 0,
A₂₃ = – 2
A₃₁ = 2,
A₃₂ = 5,
A₃₃ = 3

∴ adj (A) = \(\left[\begin{array}{rrr}
4 & 2 & 2 \\
-5 & 0 & 5 \\
1 & -2 & 3
\end{array}\right]\)

Question 13.
2x + 3y + 3z = 5, x – 2y + z = – 4, 3x – y – 2z = 3.
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{rrr}
2 & 3 & 3 \\
1 & -2 & 1 \\
3 & -1 & -2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{r}
5 \\
-4 \\
3
\end{array}\right]\)
Now, |A| = 2(4 + 1) – 3 (- 2 – 3) + 3 (- 1 + 6)
= 2(5) – 3 (- 5) + 3(5)
= 10 + 15 + 15 =40 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 5,
A₁₂ = 5,
A₁₃ = 5,
A₂₁ = 3,
A₂₂ = – 13,
A₃₂ = 11
A₃₁ = 9,
A₃₂ = 1,
A₃₃ = – 7

Question 14.
x – y + 2z = 7, 3x + 4y – 5z = – 5, 2x – y + 3z = 12.
Solution.
The given system of equations can be written in the form of AK = B,
where
A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
7 \\
-5 \\
12
\end{array}\right]\)
Now, |A| = 1 (12 – 5) + 1 (9 + 10) + 2(- 3 – 8)
= 7 + 19 – 22 = 4 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 7,
A₁₂ = -19,
A₁₃ = -11
A₂₁ = 1,
A₂₂ = – 1,
A₂₃ = – 1
A₃₁ = – 3,
A₃₂ = 11,
A₃₃ = 7

Question 15.
If A = \(\) find A^-1. Using A^-1, solve the system of equations 2x – 3y + 5z = 11, 3x + 2y – 4z = – 5, x + y – 2z = – 3
Solution.
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{rrr}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{r}
11 \\
-5 \\
-3
\end{array}\right]\)
Now, |A| = 2(- 4 + 4) + 3(- 6 + 4) + 5 (3 – 2)
= 0 – 6 + 5 = – 1 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 0,
A₁₂ = 2,
A₁₃ = 1,
A₂₁ = – 1,
A₂₂ = – 9,
A₂₃ = – 5
A₃₁ = 2,
A₃₂ = 23,
A₃₃ = 13.

Question 16.
The cost of 4 kg onion, 3kg wheat and 2 kg rice is ₹ 60. The cost of 2kg onion, 4kg wheat and 6kg rice is ₹ 90. The cost of 6 kg onion, 2 kg wheat and 3 kg rice is ₹ 70. Find the cost of each item per kg by matrix method.
Solution.
Let the cost of onions, wheat and rice per kg be ₹ x, ₹ y and ₹ z respectively.
Then, the given situation can be represented by a system of equations as
4x + 3y + 2z = 60
2x + 4y + 6z = 90
6x + 2y + 3z = 70
This system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{lll}
4 & 3 & 2 \\
2 & 4 & 6 \\
6 & 2 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
60 \\
90 \\
70
\end{array}\right]\)
∴ |A| = 4 (12 – 12) – 3 (6 – 36) + 2 (4 – 24)
= 0 + 90 – 40 = 50 ≠ 0
Thus, A is non-singular. Therefore its inverse exists.
Cofactors of A are
A₁₁ = 0,
A₁₂ = 30,
A₁₃ = – 20,
A₂₁ = – 5,
A₂₂ = 0,
A₂₃ = 10,
A₃₁ = 10,
A₃₂= – 20,
A₃₃ = 10.

∴ x = 5, y = 8 and z = 8.
Hence, the cost of onion is ₹ 5 per kg, the cost of wheat is ₹ 8 per kg and the cost of rice is ₹ 8 per kg.

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.2

Direction (1 – 5): Using the property of determinants and without expanding.

Question 1.
\(\left|\begin{array}{lll}
x & a & x+a \\
y & b & y+b \\
z & c & z+c
\end{array}\right|\) = 0
Solution.
We have, \(\left|\begin{array}{lll}
x & a & x+a \\
y & b & y+b \\
z & c & z+c
\end{array}\right|=\left|\begin{array}{lll}
x & a & a \\
y & b & b \\
z & c & c
\end{array}\right|\) = 0 [applying C₃ → C₃ – C₁]

[Since, the two columns of the determinants are identical.]

Question 2.
\(\left|\begin{array}{lll}
a-b & b-c & c-a \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\) = 0
Solution.
∆ = \(\left|\begin{array}{lll}
a-b & b-c & c-a \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\)

[applying R₁ → R + R₂]

∆ = \(\left|\begin{array}{ccc}
a-c & b-a & c-b \\
b-c & c-a & a-b \\
-(a-c) & -(b-a) & -(c-b)
\end{array}\right|=-\begin{array}{ccc}
a-c & b-a & c-b \\
b-c & c-a & a-b \\
a-c & b-a & c-b
\end{array} \mid\) = 0
[Since the two rows R₁ and R₃ are identical].

Question 3.
\(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|\) = 0
Solution.
\(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|=\left|\begin{array}{lll}
2 & 7 & 2 \\
3 & 8 & 3 \\
5 & 9 & 5
\end{array}\right|\) = 0 (applying C₃ → C₃ – 9 C₂)
[Since, two columns are identical]

Question 4.
\(\left|\begin{array}{lll}
1 & b c & a(b+c) \\
1 & c a & b(c+a) \\
1 & a b & c(a+b)
\end{array}\right|\) = 0
Solution.
∆ = \(\left|\begin{array}{lll}
1 & b c & a(b+c) \\
1 & c a & b(c+a) \\
1 & a b & c(a+b)
\end{array}\right|\)

∆ = \(\left|\begin{array}{lll}
1 & b c & a b+b c+c a \\
1 & c a & a b+b c+c a \\
1 & a b & a b+b c+c a
\end{array}\right|\) (applying C₃ → C₃ – 9 C₂)

On taking (ab + bc + ca) common from C₃, we have

∆ = (ab + bc + ca) \(\left|\begin{array}{ccc}
1 & b c & 1 \\
1 & c a & 1 \\
1 & a b & 1
\end{array}\right|\)
= 0 × (ab + bc + ca) = 0
[Since, two columns C₁ and C₃ are identical]

Question 5.
\(\left|\begin{array}{lll}
b+c & q+r & y+z \\
c+a & r+p & z+x \\
a+b & p+q & x+y
\end{array}\right|=2\left|\begin{array}{lll}
a & p & x \\
b & q & y \\
c & r & z
\end{array}\right|\)
solution.

Direction (6 – 14): By using properties of determinants.

Question 6.
\(\left|\begin{array}{ccc}
0 & a & -b \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\) = 0
Solution.
We have, ∆ = \(\left|\begin{array}{ccc}
0 & a & -b \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\)

∆ = \(=\frac{1}{c}\left|\begin{array}{ccc}
0 & a c & -b c \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\) (applying R₁ → cR₁)

∆ = \(\frac{1}{c}\left|\begin{array}{ccc}
a b & a c & 0 \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|=\frac{a}{c}\left|\begin{array}{ccc}
b & c & 0 \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\) = 0
(applying R₁ → R₁ – bR₂)
[Since, the two rows R₁ and R₃ are identical].

Question 7.
\(\left|\begin{array}{ccc}
-a^{2} & a b & a c \\
b a & -b^{2} & b c \\
c a & c b & -c^{2}
\end{array}\right|\) = 4 a² b² c²
Solution.

[Applying R₂ → R₂ + R₁ and R₃ R₃ + R₁], we have

∆ = a² b² c² \(\left|\begin{array}{ccc}
-1 & 1 & 1 \\
0 & 0 & 2 \\
0 & 2 & 0
\end{array}\right|\)

= a² b² c² \(\left|\begin{array}{ll}
0 & 2 \\
2 & 0
\end{array}\right|\)
= a² b² c² (0 – 4)
= 4 a² b² c² = R.H.S.

Question 8.
(i) \(\left|\begin{array}{lll}
1 & a & a^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\) = (a – b) (b – c) (c – a)

(ii) \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^{3} & b^{3} & c^{3}
\end{array}\right|\) = (a – b) (b – c) (c – a) (a + b + c)
Solution.
(i)

By expanding along C₁, we have

∆ = (a – b) (b – c) (c – a) \(\left|\begin{array}{cc}
0 & -1 \\
1 & b+c
\end{array}\right|\)
= (a – b) (b – c) (c – a)

(ii) Let ∆ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^{3} & b^{3} & c^{3}
\end{array}\right|\)
Applying C₁ → C₁ – C₃, C₂ → C₂ – C₃, we have

By expanding along C₁, we have
∆ = (a – b) (b – c) (c – a) (a + b + c) (- 1) \(\left|\begin{array}{cc}
0 & 1 \\
1 & c
\end{array}\right|\)
= (a – b) (b – c) (c – a) (a + b + c)

Question 9.
\(\left|\begin{array}{lll}
x & x^{2} & y z \\
y & y^{2} & z x \\
z & z^{2} & x y
\end{array}\right|\) = (x – y) (y – z) (z – x) (xy + yz + zx)
Solution.
L.H.S = \(\mid \begin{array}{lll}
x & x^{2} & y z \\
y & y^{2} & z x \\
z & z^{2} & x y
\end{array}\)

Applying R₂ → R₂ – R₁ and R₃ → R₃ – R₁, we have

∆ = \(\left|\begin{array}{ccc}
x & x^{2} & y z \\
y-x & y^{2}-x^{2} & z x-y z \\
z-x & z^{2}-x^{2} & x y-y z
\end{array}\right|\)

= (x – y) (z – x) (z – y) [(- xz – yz) + (- x² – xy + x²)]
= – (x – y) (z – x) (z – y) (xy + yz + zx)
= (x – y) (y – z) (z – x) (xy + yz + zx) = R.H.S.
Hence, the given result is proved.

Question 10.
(i) \(\left|\begin{array}{ccc}
x+4 & 2 x & 2 x \\
2 x & x+4 & 2 x \\
2 x & 2 x & x+4
\end{array}\right|\) = (5x + 4) (4 – x)²

(ii) \(\left|\begin{array}{ccc}
y+k & y & y \\
y & y+k & y \\
y & y & y+k
\end{array}\right|\) = k² (3y + k)
Solution.
(i)

= (5x + 4)(4 – x) (4 – x) \(\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 x & 1 & 0 \\
2 x & 0 & 1
\end{array}\right|\)
By expanding along C₃, have
∆ = (5x + 4) (4 – x)² \(\left|\begin{array}{cc}
1 & 0 \\
2 x & 1
\end{array}\right|\)
= (5x + 4) (4 – x)²
Hence, the given result is proved.

(ii)

Question 11.
(i) \(\left|\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\) = (a + b + c)²

(ii) \(\left|\begin{array}{ccc}
x+y+2 z & x & y \\
z & y+z+2 x & y \\
z & x & z+x+2 y
\end{array}\right|\) = 2(x + y + z)²
Solution.
(i) Let ∆ = \(\left|\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\)

Applying R₁ → R₁ + R₂ + R₃, we have
∆ = \(\left|\begin{array}{ccc}
a+b+c & a+b+c & a+b+c \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\)

= (a + b + c) \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\) (Taking out (a + b+ c) common from R₁)

Applying C₂ → C₂ – C₁ and C₃ → C₃ – C₁, we have
∆ = (a + b + c) \(\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 b & -(a+b+c) & 0 \\
2 c & 0 & -(a+b+c)
\end{array}\right|\)

= (a + b + c)³ \(\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 b & -1 & 0 \\
2 c & 0 & -1
\end{array}\right|\)

By expanding along C₃, we have
∆ = (a + b + c)³ (- 1) (- 1) = (a + b + c)³
Hence, the given result is proved.

(ii)

By expanding along R₃, we have
= 2(x + y+ z)² (1)(1 – 0) = 2(x + y+ z)³
Hence, the given result is proved.

Question 12.
\(\left|\begin{array}{ccc}
1 & x & x^{2} \\
x^{2} & 1 & x \\
x & x^{2} & 1
\end{array}\right|\) = (1 – x³)²
Solution.
∆ = \(\left|\begin{array}{ccc}
1 & x & x^{2} \\
x^{2} & 1 & x \\
x & x^{2} & 1
\end{array}\right|\)

Applying R₁ → R₁ + R₂ + R₃, we have

Question 13.
\(\left|\begin{array}{ccc}
1+a^{2}-b^{2} & 2 a b & -2 b \\
2 a b & 1-a^{2}+b^{2} & 2 a \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\) = (1 + a² + b²)³
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
1+a^{2}-b^{2} & 2 a b & -2 b \\
2 a b & 1-a^{2}+b^{2} & 2 a \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\)

Applying R₁ → R₁ + bR₂ and R₂ → R₂ – aR₃

∆ = \(\left|\begin{array}{ccc}
1+a^{2}+b^{2} & 0 & -b\left(1+a^{2}+b^{2}\right) \\
0 & 1+a^{2}+b^{2} & a\left(1+a^{2}+b^{2}\right) \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\)

= (1 + a² + b²)² \(\left|\begin{array}{ccc}
1 & 0 & -b \\
0 & 1 & a \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\)

By expanding along R₁, we have
∆ = (1 + a² + b²)² \(\left[(1)\left|\begin{array}{cc}
1 & a \\
-2 a & 1-a^{2}-b^{2}
\end{array}\right|-b\left|\begin{array}{cc}
0 & 1 \\
2 b & -2 a
\end{array}\right|\right]\)

= (1 + a² + b²)² [1 – a² – b² + 2a² – b(- 2b)]
= (1 + a² + b²)² (1 + a² + b²)
= (1 + a² + b²)³

Hence, the given result is proved.

Question 14.
\(\left|\begin{array}{ccc}
a^{2}+1 & a b & a c \\
a b & b^{2}+1 & b c \\
c a & c b & c^{2}+1
\end{array}\right|\) = 1 + a² + b² + c²
Solution.

By expanding along R₃, we have
∆ = \(-1\left|\begin{array}{cc}
b^{2} & c^{2} \\
1 & 0
\end{array}\right|+1\left|\begin{array}{cc}
a^{2}+1 & b^{2} \mid \\
-1 & 1
\end{array}\right|\)

= – 1(- c²) + (a² + 1 + b²)
= 1 + a² + b² + c²

Direction (15 – 16): Choose the correct answer in the following questions.

Question 15.
Let A be a square matrix of order 3 × 3 then |KA| is equal to
(A) k |A|
(B) k² |A|
(C) k³ |A|
(D) 3k |A|
Solution.
A is a square matrix of order 3 × 3. (Given)

Question 16.
Which of the following is correct?
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of these
Solution.
We know that to every square matrix, A [a_ij] of order n. We can associate a number called the determinant of square matrix A, where a_ij = (i, j)th element of A.
Thus, the determinant is a number associated to a square matrix. Hence, the correct answer is (C).

Punjab State Board PSEB 9th Class Physical Education Book Solutions Chapter 1 शारीरिक शिक्षा-इसके गुण एवं उद्देश्य Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Physical Education Chapter 1 शारीरिक शिक्षा-इसके गुण एवं उद्देश्य

PSEB 9th Class Physical Education Guide शारीरिक शिक्षा-इसके गुण एवं उद्देश्य Textbook Questions and Answers

बहुत छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
शारीरिक शिक्षा का लक्ष्य क्या है ?
उत्तर-
शारीरिक शिक्षा का उद्देश्य व्यक्ति के लिए ऐसा वातावरण प्रदान करना है जो उसके शरीर, दिमाग तथा समाज के लिए लाभदायक हो।

प्रश्न 2.
शारीरिक शिक्षा क्या है ?
उत्तर-
शारीरिक शिक्षा बच्चे के सम्पूर्ण व्यक्तित्व के विकास के लिए शारीरिक कार्यक्रम द्वारा, शरीर, मन तथा आत्मा को पूर्णता की ओर ले जाती है।

प्रश्न 3.
शारीरिक शिक्षा के कोई दो उद्देश्यों के नाम लिखो।
उत्तर-
(1) शारीरिक विकास (2) मानसिक विकास।

प्रश्न 4.
व्यक्ति और समाज के विकास में शारीरिक शिक्षा के कोई दो योगदानों के नाम लिखें।
उत्तर-
(1) खाली समय का उचित प्रयोग, (2) जीवन के लक्ष्य की प्राप्ति में सहायक, 3. सामाजिक भावना।

प्रश्न 5.
खेल के मैदान में आप कौन-कौन से शारीरिक शिक्षा के उद्देश्य ग्रहण करते हो ? किसी दो के नाम लिखें।
उत्तर-
(1) सहनशीलता, (2) अनुशासन, (3) चरित्र विकास ।

प्रश्न 6.
खेलें व्यक्ति में कैसे गुण विकसित करती हैं ?
उत्तर-
नेतृत्व के गुण।

बड़े उत्तरों वाले प्रश्न

प्रश्न 1.
शारीरिक शिक्षा का क्या लक्ष्य है ?
(What is the aim of Physical Education ?)
उत्तर-
शारीरिक शिक्षा का लक्ष्य (Aim of Physical Education)-शारीरिक शिक्षा साधारण शिक्षा की भान्ति उच्च मंजिल पर पहुंचने के लिए शिक्षा प्रदान करती है।
सुप्रसिद्ध शारीरिक शिक्षा शास्त्री जे० एफ० विलिअम्ज (J.F. Williams) का कहना है .. कि यदि हमें शारीरिक शिक्षा की मंजिल प्राप्त करनी है तो यह हमारा उद्देश्य होना चाहिए। शारीरिक शिक्षा का उद्देश्य एक कुशल तथा योग्य नेतृत्व देना तथा ऐसी सुविधाएं प्रदान करना है जो किसी एक व्यक्ति या समुदाय को कार्य करने का अवसर दें तथा ये सभी क्रियाएं शारीरिक रूप से सम्पूर्ण, मानसिक रूप से उत्तेजक तथा सन्तोषजनक तथा सामाजिक रूप से निपुण हों। इसके अनुसार व्यक्ति के लिए केवल उन्हीं क्रियाओं का चयन करना चाहिए जो शारीरिक रूप से लाभदायक हों।

प्रत्येक व्यक्ति केवल वे क्रियाएँ करे जो शरीर को तेज़ करने वाली हों तथा उसकी चिन्तन शक्ति बढ़ाने वाली हों। खेलों में कुछ उलझनें तथा प्रतिबन्ध इस प्रकार लगाये जाते हैं कि व्यक्ति का दिमाग ताज़ा रहे और उसे मानसिक सन्तोष मिले। इन क्रियाओं को समाज का समर्थन भी प्राप्त होना चाहिए। इसके अतिरिक्त समाज के अन्य सदस्य भी इन्हें आदर की दृष्टि से देखें। . संक्षेप में, समूचे तौर पर शारीरिक शिक्षा का लक्ष्य व्यक्ति के लिए ऐसा वातावरण प्रदान करना है जो उसके शारीरिक, मानसिक तथा सामाजिक पक्ष के लिए उपयोगी हो। इस प्रकार व्यक्ति का सर्वपक्षीय विकास (All-round Development) ही शारीरिक शिक्षा का एकमात्र लक्ष्य है।

प्रश्न 2.
खाली समय का उचित प्रयोग किस प्रकार किया जा सकता है ? संक्षेप में लिखो।
(How can Leisure time be usefully spent ? Describe in brief.)
उत्तर-
किसी ने ठीक ही कहा है कि “खाली मन शैतान का घर होता है।” (“An idle brain is a devil’s workshop.”) यह प्रायः देखा भी जाता है कि बेकार आदमी को शरारतें ही सूझती हैं। कई बार तो वह ऐसे गलत काम करने लगता है जो सामाजिक तथा नैतिक दृष्टि से उचित नहीं ठहराये जा सकते। इसका कारण यह है कि उसके पास फालतू समय तो है परन्तु उसके पास इसे व्यतीत करने का ढंग नहीं है। फालतू समय का उचित प्रयोग न होने के कारण उसका दिमाग कुरीतियों में फंस जाता है और कई बार अनेक उलझनों में उलझ कर रह जाता है जिनसे बाहर निकलना उसके वश से बाहर होता है।

यदि व्यक्ति इस फालतू समय का सदुपयोग जानता हो तो वह जीवन में उच्च शिखरों को छू सकता है। संसार के अनेक आविष्कार उन व्यक्तियों ने किये जो फालतू समय को कुशल ढंग से व्यतीत करने की कला से परिचित थे। इस प्रकार संसार के अनेक आविष्कार फालतू समय की ही देन हैं।।

यदि बच्चों के फालतू समय व्यतीत करने के लिए कोई उचित प्रबन्ध न हो तो वे बुरी आदतों का शिकार हो जाएंगे। इस प्रकार वे समाज पर बोझ बनने के साथ-साथ इसके लिए कलंक भी बन जाएंगे। इसलिए उनके फालतू समय के उचित प्रयोग की अच्छी व्यवस्था करनी चाहिए। स्कूलों, कॉलेजों, पंचायतों या नगरपालिकाओं या सरकार को अच्छे खेल के मैदानों तथा खेलों के सामान का पूरा प्रबन्ध करना चाहिए ताकि बच्चे खेलों में भाग लेकर अपने खाली समय का उचित प्रयोग कर सकें। इस प्रकार हम देखते हैं कि फालतू समय के प्रभावशाली उपयोग का सर्वोत्तम साधन खेलें हैं।

प्रश्न 3.
‘खेलें अच्छे नेता बनाती हैं।’ कैसे ?
(Games make good Leader. How ?)
अथवा
खेलें एक अच्छे नेता के गुण कैसे पैदा करती हैं?
(How sports produce the qualities of a good Leader ?)
उत्तर-
खेलें व्यक्ति में अच्छे नेतृत्व के गुण विकसित करती हैं। शारीरिक शिक्षा का क्षेत्र अत्यधिक विशाल है। खेलों में एक खिलाड़ी को अनेक ऐसे अवसर मिलते हैं जब उसे टीम के कप्तान, सैक्रेटरी, रैफरी या अम्पायर की भूमिका निभानी पड़ती है। इन परिस्थितियों में वह अपनी योग्यता के अनुसार आचरण करता है। एक कप्तान के रूप में वह अपनी टीम के खिलाड़ियों को समय-समय पर निर्देश देकर उन्हें उचित ढंग से तथा पूर्ण विश्वास के साथ खेलने की प्रेरणा देता है। एक रैफरी या अम्पायर के रूप में वह निष्पक्ष रूप से उचित निर्णय देता है। सैक्रेटरी के रूप में वह टीम का ठीक ढंग से गठन एवं संचालन करता है। इस प्रकार उसमें एक सफल और अच्छे नेता के गुण विकसित हो जाते हैं।

एक नेता में अच्छे चारित्रिक गुणों का होना आवश्यक है। उसमें आज्ञा-पालन, समय की पाबन्दी, सभी के साथ समान व्यवहार, प्रेम, सहानुभूति, सहनशीलता आदि गुण प्रचुर मात्रा में होने चाहिएं। ये सभी गुण वह खेल के मैदान से ग्रहण कर सकता है। एक नेता को अपने आस-पास के लोगों के साथ सद्भावना से रहना चाहिए। खेलें उसमें यह गुण विकसित करती हैं। जब एक खिलाड़ी अन्य स्थानों के खिलाड़ियों के साथ मिल-जुल कर खेलता है, वह उनके स्वभाव तथा सभ्यता के साथ भली-भान्ति परिचित हो जाता है। उसमें उनके प्रति सद्भावना उत्पन्न हो जाती है। यह सद्भावना ही एक नेता का महत्त्वपूर्ण गुण है।

नेता को चुस्त और फुर्तीला होना चाहिए। खेलों में भाग लेने से व्यक्ति में चुस्ती और स्फूर्ति आती है। इस प्रकार खेलें अच्छे नेताओं के निर्माण में विशेष योगदान देती हैं।

बड़े स्तरों वाले प्रश्न

प्रश्न 1.
शारीरिक शिक्षा के मुख्य उद्देश्य कौन-कौन से हैं ?
(Describe the main objectives of Physical Education.)
उत्तर-
शारीरिक शिक्षा के उद्देश्य (Objectives of Physical Education)किसी भी कार्य को आरम्भ करने से पहले उसके उद्देश्य निर्धारित कर लेना आवश्यक है। बिना उद्देश्य के किया गया काम छाछ को मथने के समान है। उद्देश्य निश्चित कर लेने से
हमारे यत्नों को प्रोत्साहन मिलता है और उस काम को करने में लगाई गई शक्ति व्यर्थ नहीं जाती है। आज तो शारीरिक शिक्षा के उद्देश्य की जानकारी प्राप्त करना और भी ज़रूरी हो गया है क्योंकि अब तो स्कूलों में एक विषय (Subject) के रूप में इसका अध्ययन किया जाता है।

साधारणतया शारीरिक शिक्षा के निम्नलिखित उद्देश्य हैं-

• शारीरिक वृद्धि एवं विकास (Physical Growth and Development)
• मानसिक विकास (Mental Development) (3) सामाजिक विकास (Social Development)
• चरित्र निर्माण या नैतिक विकास (Formation of Character or Moral Development)
• नाड़ियों और मांसपेशियों में समन्वय (Neuro-muscular Co-ordination )
• बीमारियों से बचाव (Prevention of Diseases)

1. शारीरिक वृद्धि एवं विकास (Physical Growth and Development)अच्छा, सफल तथा सुखद जीवन व्यतीत करने के लिए सुदृढ़, सुडौल तथा स्वस्थ शरीर का होना परमावश्यक है। हमारे शरीर का निर्माण मज़बूत हड्डियों से हुआ है। इसमें काम करने वाले सभी अंग उचित रूप से अपने कर्तव्य का पालन कर रहे हैं। शरीर के अंगों के सुचारु रूप से कार्य करते रहने से शरीर का निरन्तर विकास होता है। इसके विपरीत इनके भलीभान्ति काम न करने से शारीरिक विकास भी रुक जाता है। इस प्रकार शारीरिक प्रफुल्लता के उद्देश्य की प्राप्ति के लिए शारीरिक शिक्षा सुखद वातावरण जुटाती है।

2. मानसिक विकास (Mental Development)- शारीरिक विकास के साथसाथ मानसिक विकास की भी आवश्यकता है। शारीरिक शिक्षा ऐसी क्रियाएं प्रदान करती हैं जो व्यक्ति के मस्तिष्क को उत्तेजित करती हैं। उदाहरणस्वरूप, बास्केटबाल के खेल में एक टीम के खिलाड़ियों को विरोधी टीम के खिलाड़ियों से गेंद (बॉल) को बचा कर रखना होता है तथा इसके साथ-साथ अपना लक्ष्य भी देखना पड़ता है । अपनी शक्ति का अनुमान लगा कर बॉल को ऊपर लगी बास्केट में भी डालना होता है। कोई भी खिलाड़ी जो शारीरिक रूप से हृष्ट-पुष्ट है, परन्तु मानसिक रूप में विकसित नहीं है, कभी भी अच्छा खिलाड़ी नहीं बन सकता है। शारीरिक शिक्षा मानसिक विकास के लिए उचित वातावरण प्रदान करती है। इसलिए खेलों में भाग लेने वाले व्यक्ति का शारीरिक विकास के साथ-साथ मानसिक विकास भी हो जाता है।

प्रायः शारीरिक रूप से अस्वस्थ तथा मानसिक रूप से सुस्त व्यक्ति बहुत ही भावुक हो जाते हैं। वे जीवन की साधारण समस्याओं को हंसी-हंसी में सुलझा लेने के स्थान पर उनमें उलझ कर रह जाते हैं। वे अपनी खुशी, गम, पसन्द तथा नफ़रत को आवश्यकता से कहीं अधिक महत्त्व देने लगते हैं और वे अपना कीमती समय तथा शक्ति व्यर्थ ही गंवा देते हैं। इस प्रकार कोई महान् सफलता प्राप्त करने से वंचित रह जाते हैं। शारीरिक शिक्षा इन भावनाओं पर नियन्त्रण पाने की कला सिखाती है।

3. सामाजिक विकास (Social Development) शारीरिक शिक्षा व्यक्ति को अपने इर्द-गिर्द के लोगों के साथ सद्भावना से रहने की शिक्षा प्रदान करती है। जब एक व्यक्ति विभिन्न स्थानों के खिलाड़ियों के साथ मिल कर खेलता है तो सामाजिक विकास का अच्छा वातावरण पनपता रहता है। प्रत्येक खिलाड़ी अन्य खिलाड़ियों के स्वभाव, रीति-रिवाज, पहनावा, सभ्यता तथा संस्कृति से भली-भान्ति परिचित हो जाता है। कई बार दूसरों की अच्छी बातें तथा गुण ग्रहण कर लिए जाते हैं। देखने में आता है कि यूनिवर्सिटी, राज्यीय, राष्ट्रीय तथा अन्तर्राष्ट्रीय स्तरों पर खेल मुकाबलों का आयोजन किया जाता है। इनका मुख्य उद्देश्य लोगों में प्रेम तथा आदर की भावनाएं विकसित करना होता है।

4. चरित्र-निर्माण अथवा नैतिक विकास (Character Formation or Moral Development)-खेल का मैदान चरित्र-निर्माण की पाठशाला है। इसका कारण यह है कि खेल के मैदान में ही व्यक्ति खेल के नियमों को निभाते हैं। यहीं से वे अच्छा जीवन व्यतीत करने की कला सीखते हैं तथा सुलझे हुए इन्सान बन जाते हैं। खेल खेलते समय यदि रैफरी कोई ऐसा निर्णय दे देता है जो उन्हें पसन्द नहीं तो भी वे खेल जारी रखते हैं और कोई अभद्र व्यवहार नहीं करते। खेल के मैदान में ही आज्ञा-पालन, अनुशासन, प्रेम तथा दूसरों से सहयोग आदि के गुण सीखे जाते हैं। इस प्रकार प्रत्येक व्यक्ति का चरित्र-निर्माण और नैतिक विकास होता है।

5. नाड़ियों और मांसपेशियों में समन्वय (Neuro-muscular Coordination)-हमारी प्रतिदिन की क्रियाओं को समुचित ढंग से पूर्ण करना अनिवार्य है ताकि नाड़ियों और मांसपेशियों में समन्वय पैदा हो। शारीरिक शिक्षा इनमें समन्वय पैदा करने में सहायता देती है।

6. बीमारियों से बचाव (Prevention from Diseases) शारीरिक शिक्षा का उद्देश्य विद्यार्थियों को बीमारी से बचाना भी है। बहुत-सी बीमारियां अज्ञानता के कारण लग जाती हैं। शारीरिक शिक्षा का उद्देश्य बच्चों की बीमारियों के कारणों का ज्ञान देना है। वे इन कारणों से बच कर स्वयं भी बीमारियों से बच सकते हैं।

अन्त में, हम कह सकते हैं कि शारीरिक शिक्षा मनुष्य के सर्वपक्षीय विकास के लिए, नागरिकता के लिए, मानवीय भावनाओं के निर्माण तथा राष्ट्रीय एकता के लिए बहुत ही उपयोगी है।

प्रश्न 2.
हॉकी के खेल के मैदान में आप कौन-कौन से शारीरिक शिक्षा के उद्देश्य ग्रहण करते हो ?
(What are the objectives of Physical Education that one acquires in the game of Hockey ?)
उत्तर-
हॉकी का मैदान भी एक तरह की पाठशाला है जहां से विद्यार्थी शारीरिक शिक्षा के अनेक गुण ग्रहण करता है जिनसे वह जीवन में उन्नति के उच्च शिखर को छूता है और जीवन का हर पक्ष से भरपूर आनन्द उठाता है। हॉकी के क्रीड़ा-क्षेत्र में हम शारीरिक शिक्षा के निम्नलिखित गुणों को ग्रहण करते हैं –

1. सहनशीलता (Toleration) खेल के मैदान में हम सहनशीलता का पाठ पढ़ते हैं। वैसे तो सभी खिलाड़ी चाहते हैं कि जीत उनकी टीम की ही हो। परन्तु कई बार लाख चाहने पर भी विरोधी टीम विजयी हो जाती है। ऐसी स्थिति में पराजित टीम के खिलाड़ी दिल छोड़ कर नहीं बैठ जाते बल्कि अपना मनोबल ऊंचा रखते हैं। वे हार-जीत को एक ही समान समझते हैं। इस प्रकार खेल के मैदान से विद्यार्थियों को सहनशीलता की व्यावहारिक ट्रेनिंग मिलती है।

2. अनुशासन (Discipline)-खेल के मैदान में खिलाड़ी अनुशासन में रहने की कला सीखते हैं। उन्हें पता चलता है कि अनुशासन ही सफलता की कुंजी है। वे खेल में भाग लेते समय अनुशासन का पालन करते हैं। वे अपने कप्तान की आज्ञा मानते हैं तथा रैफरी के निर्णयों को सहर्ष स्वीकार करते हैं। खेल में पराजय को सामने स्पष्ट शारीरिक शिक्षा-इसके गुण एवं उद्देश्य देखते हुए भी वे कोई ऐसा अभद्र व्यवहार नहीं करते जिससे कोई उन्हें अनुशासनहीन – कह सके।

3. चरित्र विकास (Character Development) हॉकी के खेल में भाग लेने से विद्यार्थियों में सहयोग, प्रेम, सहनशीलता, अनुशासन आदि गुणों का विकास होता है जिनसे उनके चरित्र का विकास होता है। इस खेल में भाग लेने से उनमें सहयोग की भावना विकसित होती है। वे निजी हितों को समूचे हितों पर न्योछावर कर देते हैं।

4. व्यक्तित्व का विकास (Development of Personality) हॉकी के खेल में भाग लेने से विद्यार्थियों में कुछ ऐसे गुण विकसित हो जाते हैं, जिनसे उनके व्यक्तित्व का विकास हो जाता है। उनमें सहयोग तथा सहनशीलता आदि गुण विकसित होते हैं तथा उनका शरीर सुन्दर एवं आकर्षक बन जाता है। ये सभी अच्छे व्यक्तित्व के चिन्ह हैं।

5. अच्छे नागरिक बनाना (Creation of Good Citizens)-हॉकी के मैदान में खिलाड़ी में कर्त्तव्य-पालन, आज्ञा पालन, सहयोग, सहनशीलता आदि गुण विकसित हो जाते हैं जो उन्हें एक अच्छा नागरिक बनने में पर्याप्त सहायता पहुंचाते हैं। वे नागरिकता के सभी कर्तव्यों का भली-भान्ति पालन करते हैं। इस प्रकार हॉकी का मैदान अच्छे नागरिकों के निर्माण में महत्त्वपूर्ण भूमिका निभाता है।

6. सहयोग (Co-operation) हॉकी के खेल में भाग लेने वाला खिलाड़ी प्रत्येक खिलाड़ी का कहना मानता है। वह अपना विचार दूसरों पर बलात् लागू नहीं करवाता है, अपितु अपने विचार विनिमय के द्वारा खेल के मैदान में संयुक्त विचारधारा बनाता है। इस प्रकार सहयोग की भावना उत्पन्न होती है।

7. राष्ट्रीय भावना (National Spirit)-हॉकी का मैदान एक ऐसा स्थान है जहां हम बिना धर्म और वर्ग के आधार पर भाग ले सकते हैं। कोई भी खिलाड़ी खेल के मैदान में से किसी खिलाड़ी को धर्म के आधार पर टीम से बाहर नहीं निकाल सकता। इस प्रकार . खेल के मैदान में समानता और राष्ट्रीय एकता की भावना पैदा होती है।

8. आत्म-विश्वास की भावना (Self-Confidence) हॉकी के खेल के मैदान में खिलाड़ियों में आत्म-विश्वास की भावना पैदा होती है। जैसे, वह विजय-पराजय को एक समान समझता है। वही खिलाड़ी खेल के मैदान में सफल होता है जो धैर्य
और विश्वास के साथ खेले। इससे सिद्ध होता है कि हॉकी के खेल के द्वारा खिलाड़ियों में आत्म-विश्वास की भावना पैदा होती है।

9. विजय-पराजय को समान समझने की भावना (Spirit of giving equal importance to Victory of Defeat) हॉकी के खेल के द्वारा खिलाड़ियों में विजय-पराजय को एक समान समझने की भावना पैदा होती है।

हमें कभी भी विरोधी टीम का मज़ाक नहीं उड़ाना चाहिए या विजय की प्रसन्नता में पागल नहीं होना चाहिए। पराजित टीम को सदैव प्रोत्साहन देना चाहिए। यदि उसकी पराजय होती है तो उसे निराश और उत्साहहीन नहीं होने देना चाहिए अपितु उसका हौसला बढ़ाना चाहिए।

10. त्याग की भावना (Spirit of Sacrifice)-हॉकी के खेल के मैदान में त्याग की भावना अत्यावश्यक है। जब हम खेल में भाग लेते हैं तो हम अपने स्कूल, प्रान्त, क्षेत्र और सारे राष्ट्र के लिए अपने हित का त्याग करके उसकी विजय का श्रेय राष्ट्र को देते हैं। अत: यह सिद्ध होता है कि खेलें सदैव त्याग चाहती हैं। – ड्यूक ऑफ़ विलिंग्टन ने नेपोलियन को वाटरलू (Waterloo) के युद्ध में पराजित करने के पश्चात् कहा था, “वाटरलू का युद्ध एटन और हैरो के खेल के मैदानों में जीता गया।” (“The Battle of Waterloo was won at the playing-fields of Eton and Harrow.”)
इससे यह सिद्ध होता है कि खेलें अच्छे नेता पैदा करने में सहायक होती हैं।

शारीरिक शिक्षा-इसके गुण एवं उद्देश्य PSEB 9th Class Physical Education Notes

• .शारीरिक शिक्षा-शारीरिक क्रियाओं से हमें जो अनुभव प्राप्त होता है, उसे शारीरिक शिक्षा कहते हैं।
• शारीरिक शिक्षा का लक्ष्य-मनुष्य का सर्वोन्मुखी विकास ही शारीरिक शिक्षा का लक्ष्य है।
• शारीरिक शिक्षा के उद्देश्य-शारीरिक, मानसिक और नैतिक विकास ही शारीरिक शिक्षा के उद्देश्य हैं।
• खेल के मैदान में शारीरिक शिक्षा का उद्देश्य-खेल के मैदान से सहनशीलता, अनुशासन और चरित्र का विकास होता है।
• खाली समय का उचित प्रयोग-खेलों में भाग लेने से बच्चे खाली समय का उचित प्रयोग करते हैं जिससे उनमें बुरी आदतें नहीं पनपती हैं।
• खेलों के नेतृत्व का गुण-एक नेता में अच्छे चारित्रिक गुणों का होना आवश्यक है और ये खेलें मनुष्य में नेतृत्व के गुण पैदा करती हैं।