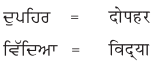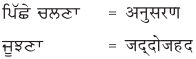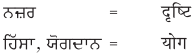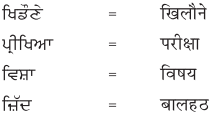Punjab State Board PSEB 8th Class Hindi Book Solutions Chapter 9 मन के जीते जीत Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Hindi Chapter 9 मन के जीते जीत (2nd Language)
Hindi Guide for Class 8 PSEB मन के जीते जीत Textbook Questions and Answers
![]()
मन के जीते जीत अभ्यास
1. नीचे गुरुमुखी और देवनागरी लिपि में दिये गये शब्दों को पढ़ें और हिंदी शब्दों को लिखने का अभ्यास करें :


उत्तर :
छात्र स्वयं अभ्यास करें।
![]()
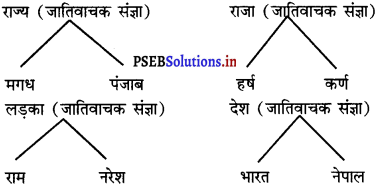
2. नीचे एक ही अर्थ के लिए पंजाबी और हिंदी भाषा में शब्द दिये गये हैं। इन्हें ध्यान से पढ़ें और हिंदी शब्दों को लिखें :


उत्तर :
छात्र स्वयं पढ़ें एवं लिखें।
3. शब्दार्थ :
- विकलांग = अंग से हीन, बेकाम अंग वाला
- अनथक = न थकने वाला
- दूषित – गंदा, मैला
- कर्णप्रिय = कानों को प्रिय लगने वाला
- विभूतियाँ – ऐश्वर्यशाली व्यक्तित्व
- अस्थि = हड्डी
- अन्यत्र = दूसरी जगह, और कहीं
- व्यक्तित्व = व्यक्ति की विशेषता या गुण
- कंठहार = गले का हार
- एकाग्रता = तल्लीन होने का भाव
- बुलंदी = ऊँचाई, उत्कर्ष
- जज़्बा = भाव, जोश, भावना
उत्तर :
छात्र स्वयं अभ्यास करें।
4. इन प्रश्नों के उत्तर एक या दो वाक्यों में लिखें :
(क) जीवन में मुश्किलों से पार कौन लोग जा पाते हैं ?
उत्तर :
जीवन में मुश्किलों से पार वही लोग जा पाते हैं जो मुसीबतों और रुकावटों के आगे सिर नहीं झुकाते। उनका साहस एवं दृढ़ विश्वास के साथ सामना करते हैं।
(ख) राजा जनक के दरबार में अष्टावक्र को देखकर सभी क्यों हँसने लगे?
उत्तर :
राजा जनक के दरबार में अष्टावक्र को देखकर सभी हँसने लगे क्योंकि उनका शरीर टेढ़ा-मेढ़ा था। उनके शरीर में आठ वक्र थे।
![]()
(ग) राजा जनक तथा दरबारी अष्टावक्र के सामने क्यों नतमस्तक हुए?
उत्तर :
अष्टावक्र के ज्ञान विद्वता के कारण राजा जनक तथा दरबारी नतमस्तक हो गए।
(घ) सूरदास ने किसकी आराधना में काव्य रचना की?
उत्तर :
सूरदास ने श्रीकृष्ण की आराधना में काव्य रचना की।
(ङ) जायसी के प्रसिद्ध महाकाव्य का नाम लिखें।
उत्तर :
पद्मावत।
(च) रामानन्द सागर द्वारा टेलीविज़न पर प्रसारित प्रख्यात धारावाहिक ‘रामायण’ में संगीत मुख्य रूप से किसने दिया?
उत्तर :
रवीन्द्र जैन ने रामायण में संगीत दिया।
(छ) बिजली के बल्ब का आविष्कार किसने किया?
उत्तर :
थामस अल्वा एडीसन ने बिजली के बल्ब का आविष्कार किया।
(ज) ब्रेल लिपि का आविष्कार किसने किया?
उत्तर :
ब्रेल लिपि का आविष्कार लई ब्रेल ने किया।
(झ) महाराजा रणजीत सिंह ने कितनी आयु में लाहौर पर अधिकार कर लिया था?
उत्तर :
उन्नीस वर्ष की आयु में।
![]()
(ज) बाबा आम्टे को भारत सरकार ने समाज सेवा के लिए पद्मश्री तथा पद्मभूषण का सम्मान कब दिया?
उत्तर :
बाबा आम्टे को भारत सरकार ने समाज सेवा के लिए पद्मश्री 1971 ई० में तथा पद्मभूषण सन् 1986 ई० में दिया।
5. इन प्रश्नों के उत्तर लगभग चार या पाँच वाक्यों में लिखें :
(क) राजा जनक के दरबार में अष्टावक्र को देखकर जब सभी हँसने लगे तो अष्टावक्र ने क्या कहा?
उत्तर :
अष्टावक्र ने कहा कि गन्ने के टेढ़े-मेढ़े होने से उसकी मिठास में कमी नहीं आती। फूल की पंखुड़ी के टेढ़े होने से उसकी खुशबू खत्म नहीं हो जाती और नदी की धारा के टेढ़े होने से उसका जल दूषित नहीं हो जाता।
(ख) शेरशाह क्यों लज्जित हुआ और उसने जायसी को क्यों सम्मान दिया?
उत्तर :
जायसी के मुख से मोहि का हँससि के कोहरहिं? अर्थात् तुम मुझ पर हँसे हो अथवा उस ईश्वर रूपी कुम्हार पर हँस रहे हो यह सुनकर शेरशाह लज्जित हुआ और उसने जायसी को उनकी विद्वता के कारण सम्मान दिया।
(ग) थामस एडीसन के ध्वनि संबंधी आविष्कारों से लोग क्यों आश्चर्यचकित हो जाते थे?
उत्तर :
लोग इसलिए आश्चर्यचकित हो जाते थे कि जो व्यक्ति पूरी तरह स्वयं नहीं सुन सकता। वह किस प्रकार ध्वनि के हर पहलू को अच्छी प्रकार से समझ लेता है।
(घ) लुई ब्रेल द्वारा नेत्रहीनों के पढ़ने के लिए बनाई लिपि की क्या विशेषता है?
उत्तर :
ब्रेल लिपि कागज़ पर उभरे हुए चिहन होते हैं जिन्हें स्पर्श करके लोग पढ़ते हैं।
![]()
(ङ) बाबा आम्टे का समाज सेवा में क्या योगदान रहा?
उत्तर :
बाबा आम्टे सारी उम्र कुष्ठ रोगियों तथा समाज से परित्यक्त लोगों की सेवा में लगे रहे। इन्हीं की प्रेरणा से आनंदवन आश्रम के अनेक कुष्ठ रोगियों ने भीख मांगना छोड़कर स्वयं श्रम करना आरंभ कर दिया। इस तरह बाबा आम्टे का समाज सेवा में महान् योगदान रहा है।
(च) भारतीय स्पिनर चन्द्रशेखर का क्रिकेट में क्या योगदान रहा?
उत्तर :
चंद्रशेखर का एक हाथ पोलियोग्रस्त हो गया था किन्तु वह इसी हाथ से गेंदबाजी करते थे और बल्लेबाजों को पैविलियन पहुंचा देते थे। उन्होंने 58 टैस्ट मैच खेले तथा 7199 रन देकर 242 विकेट लिए।
(छ) राणा सांगा और महाराजा रणजीत सिंह की वीरता के विषय में आप क्या जानते हैं ?
उत्तर :
राणा सांगा की वीरता एवं साहस से बड़े-बड़े शासक थर-थर काँपते थे। उन्होंने इब्राहिम लोदी जैसे अनेक शत्रुओं को पराजित किया। महाराजा रणजीत सिंह ने अपनी वीरता से केवल उन्नीस वर्ष की आयु में लाहौर पर अधिकार कर लिया था। इसके बाद धीरे-धीरे जम्मू कश्मीर, अमृतसर, मुलतान, पेशावर आदि पर अधिकार कर लिया।
(ज) भाग्य संवरता नहीं, संवारना पड़ता है – इन पंक्तियों में लेखक क्या कहना चाहता है ?
उत्तर :
इन पंक्तियों में लेखक कहना चाहता है कि व्यक्ति का भाग्य अपने आप नहीं संवरता बल्कि वह परिश्रम, आत्मविश्वास एवं दृढ़ निश्चय से बदला जाता है। इसके लिए हमें लगातार कठिन संघर्ष करना पड़ता है।
![]()
6. इन मुहावरों के अर्थ बताते हुए उन्हें वाक्यों में प्रयोग करें :
- घुटने टेकना
- सिर न झुकाना
- दाँत खट्टे करना
- लोहा मनवाना
- थर-थर काँपना
- बुलंदियाँ छूना
उत्तर :
- घुटने टेकना = हारना-दुश्मनों ने भारतीय सेना के सामने घुटने टेक दिए।
- सिर न झुकाना = हार न मानना-साहसी लोग कभी मुसीबतों के सामने सिर नहीं झुकाते।
- दाँत खट्टे करना = बुरी तरह हराना-कारगिल में भारतीय सेना ने शत्रुओं के दाँत खट्टे कर दिए।
- लोहा मनवाना = जय-जयकार करवाना-महाराजा रणजीत सिंह ने अपने साहस एवं बल से दुनिया में लोहा मनवाया।
- थर-थर काँपना = डरना-शेर को देखकर रवि थर-थर काँपने लगा।
- बुलंदियाँ छूना = तरक्की करना-रवि अपनी मेहनत से बुलंदियाँ छू रहा है।
7. इन शब्दों के दो-दो पर्यायवाची शब्द लिखें :
- चुनौती = _____________
- सेवा = _____________
- अनूठा =_____________
- पुरस्कार = _____________
- दृढ़ता = _____________
- हाथ = _____________
- उपहास =_____________
- अधिकार = _____________
- शक्ति = _____________
- भाग्य = _____________
- मस्तिष्क = _____________
- लक्ष्य = _____________
- प्रयत्न = _____________
- पैर = _____________
- अध्यापक = _____________
- अंधकार = _____________
- लज्जित = _____________
- जल = _____________
उत्तर :
- चुनौती = ललकार, आह्वान
- सेवा = परिचर्या, खिदमत
- अनूठा = अनुपम, अनोखा
- पुरस्कार = उपहार, इनाम
- दृढ़ता = मज़बूती, प्रगाढ़ता
- हाथ = हस्त, कर
- उपहास = हँसी, दिल्लगी
- अधिकार = हक़, प्रभुत्व
- शक्ति = बल, पौरुष
- भाग्य = किस्मत, तकदीर
- मस्तिष्क = भेजा, दिमाग
- लक्ष्य = मंजिल, उद्देश्य
- प्रयत्न = प्रयास, कोशिश
- पैर = पाँव, चरण
- अध्यापक = शिक्षक, गुरु
- अंधकार = अन्धेरा, तम
- लज्जित = शर्मसार, शर्मिंदा
- जल = पानी, नीर।
![]()
8. अनेक शब्दों के लिए एक शब्द लिखें :
- जिसे आँखों से दिखाई न देता हो _____________
- गले का हार _____________
- संगीत देने वाला _____________
- अपने पर विश्वास होना _____________
- जिसका कोई मोल न हो _____________
- कानों को प्रिय लगने वाला _____________
- आविष्कार करने वाला _____________
उत्तर :
- जिसे आँखों से दिखाई न देता हो – नेत्रहीन
- गले का हार – कंठहार
- संगीत देने वाला – संगीतकार
- अपने पर विश्वास होना – आत्मविश्वास
- जिसका कोई मोल न हो – अनमोल
- कानों को प्रिय लगने वाला – कर्णप्रिय
- आविष्कार करने वाला – आविष्कारक
रचनात्मक अभिव्यक्ति :
(क) मौखिक अभिव्यक्ति – इस पाठ में आप किस महान विभूति से प्रेरित हुए हैं ? क्यों ?
उत्तर :
इस पाठ में अनेक महान् विभूतियां हैं जिन्होंने अपनी विकलांगता पर विजय पाकर भी महानता प्राप्त की। हम महाराणा रणजीत सिंह से प्रेरित हुए क्योंकि वे अधिक साहसी, वीर बलशाली, निडर योद्धा थे। वे बहुत दयालु, दयावान एवं धैर्यशाली थे।
(ख) लिखित अभिव्यक्ति – मन के जीते जीत, मन के हारे हार है– पर पाँच-सात वाक्य लिखें।
उत्तर :
- मन पर विजय पाने से ही उन्नति होती है।
- मन विजयी है तो तभी मनुष्य विकास कर सकता है।
- यदि मन हार जाए तो आदमी हार जाता है।
- मन की जीत से ही जीवन का विकास सम्भव हो सकता है।
- मन सभी ज्ञानेन्द्रिय से महत्त्वपूर्ण है।
- वह मन एक सारथि के समान है जो अन्य सभी को अपने अनुसार चलाता है।
![]()
10. इस पाठ में आए ‘र’ वर्ण के प्रयोग वाले शब्द ढूँढकर लिखें :

उत्तर
[ र ] : भारत, राणा, द्वारा
[ ‘ ] : स्पर्श, अर्जुन, दुर्लभ
[ , ] : अष्टावक्र, ब्रेल, माइक्रोफोन
[ ^ ] : रवीन्द्र, महाराष्ट्र, केन्द्रित।
11. इन शब्दों के विशेषण बनाएं :
भारत _____________
सम्मान _____________
स्वर्ग _____________
साहित्य _____________
प्रभाव _____________
दया _____________
परीक्षोपयोगी अन्य प्रश्नोत्तर
प्रश्न 1.
मनुष्य कब निराश एवं हताश हो जाता है?
उत्तर :
जब मनुष्य के अपने जीवन में चारों तरफ अंधेरा दिखाई देता है। कहीं कोई रास्ता नजर नहीं आता। वह संघर्ष करने की अपेक्षा अपने भाग्य को कोसने लगता है तब निराश एवं हताश हो जाता है।
![]()
प्रश्न 2.
अपने भाग्य को कौन लोग कोसते हैं?
उत्तर :
जो लोग मुसीबतों एवं रुकावटों का डटकर सामना नहीं करते और उनके आगे हार मान लेते हैं वही भाग्य को कोसते हैं।
प्रश्न 3.
मुश्किलों से कौन लोग पार पा सकते हैं?
उत्तर :
मुश्किलों से वही लोग पार पा सकते हैं कि जो उनके आगे सिर नहीं झुकाते बल्कि उनका साहस, आत्मविश्वास एवं दृढ़ता से सामना करते हैं।
प्रश्न 4.
लेखक ने किन-किन महान् विभूतियों का चित्रण किया है?
उत्तर :
लेखक ने निम्नलिखित महान् विभूतियों का चित्रण किया है
- अष्टावक्र
- सूरदास
- जायसी
- भारतीय संगीतकार रवीन्द्र जैन
- विश्व के महान् आविष्कारक थामस अल्वा एडीसन
- लुई ब्रेल
- बाबा आम्टे
- भारतीय स्पिनर चंद्रशेखर
- राणा सांगा
- महाराजा रणजीत सिंह।
प्रश्न 5.
महाराजा रणजीत सिंह का चरित्र-चित्रण कीजिए।
उत्तर :
महाराजा रणजीत सिंह के चरित्र की निम्नलिखित विशेषताएं हैं
- महान् वीर-महाराजा रणजीत सिंह एक महान् वीर सेनानी थे।
- न्याय प्रिय-वे बहुत न्यायप्रिय शासक थे।
- दयालुता-वे बहुत दयालु थे। उनकी दयालुता सुप्रसिद्ध है।
- दानशीलता-वे गरीबों को बहुत दान दिया करते थे। उनकी दानशीलता चारों ओर प्रसिद्ध है।
![]()
प्रश्न 6.
भक्तिकाल में सूरदास पर एक नोट लिखो।
उत्तर :
हिन्दी-साहित्य के भक्तिकाल में सूरदास का नाम बहुत प्रसिद्ध है। वे जन्म से ही नेत्रहीन थे। उन्होंने अपने आराध्य श्रीकृष्ण की लीलाओं का बहुत सजीव एवं प्रभावशाली ढंग से वर्णन किया है। उन जैसा लीला वर्णन अन्यत्र दुलर्भ है। उनकी अमरवाणी जन-जन का कंठहार बनी हुई है।
प्रश्न 7.
रवीन्द्र जैन कौन थे? उनके चरित्र की विशेषताएं लिखिए।
उत्तर :
रवीन्द्र जैन भारतीय सिनेमा के सुप्रसिद्ध संगीतकार थे। उनके चरित्र की विशेषताएं निम्नलिखित हैं
- दृढ़ इच्छा शक्ति-उनमें दृढ़ इच्छा शक्ति थी।
- एकाग्रता-उनका मन एकाग्रता से मुक्त था। इसी के कारण वे महान् बने।
- आत्मविश्वास-उनमें अटूट आत्मविश्वास था।
प्रश्न 8.
थामस अल्वा एडीसन ने कौन-से आविष्कार किए हैं?
उत्तर :
थामस अल्वा एडीसन ने बल्ब, माइक्रोफोन, फोनोग्राफ, कार्बन टेलिफोन, ट्रांसमीटर आदि हजारों आविष्कार किए हैं।
प्रश्न 9.
निम्नलिखित सही कथन पर सही (✓) और गलत कथन पर गलत (✗) का निशान लगाइए:
(क) धर्म शब्द में आधे ‘र’ (रेफ) का प्रयोग हुआ है।
उत्तर :
(✓) सही।
![]()
बहुविकल्पीय प्रश्न
निम्नलिखित प्रश्नों के उत्तर सही विकल्प चुनकर लिखें :
प्रश्न 1.
जीवन में आने वाली मुश्किलों का करना चाहिए
(क) घबराना चाहिए
(ख) भागना चाहिए
(ग) सामना करना चाहिए
(घ) आँखें मूंद लेना चाहिए।
उत्तर :
(ग) सामना करना चाहिए
प्रश्न 2.
अष्टावक्र किस युग में हुए थे?
(क) सतयुग
(ख) त्रेतायुग
(ग) द्वापर युग
(घ) कलयुग।
उत्तर :
(ख) त्रेतायुग
प्रश्न 3.
अष्टावक्र किसके दरबार में गए थे?
(क) दशरथ
(ख) जनक
(ग) रावण
(घ) बालि।
उत्तर :
(ख) जनक
![]()
प्रश्न 4.
अष्टावक्र के किस गुण से सभी नतमस्तक हुए?
(क) वीरता
(ख) दया
(ग) विद्वता
(घ) करुणा।
उत्तर :
(ग) विद्वता
प्रश्न 5.
भक्तिकाल में प्रसिद्ध कृष्णभक्त जन्मांध कवि कौन था?
(क) नंददास
(ख) सूरदास
(ग) कृष्णदास
(घ) गोपालदास।
उत्तर :
(ख) सूरदास
प्रश्न 6.
शेरशाह ने किस कवि का उपहास उड़ाया था?
(क) रसखान
(ख) जायसी
(ग) सूरदास
(घ) रामदास।
उत्तर :
(ख) जायसी
![]()
प्रश्न 7.
रवीन्द्र जैन फिल्म जगत के क्या थे?
(क) निर्देशक
(ख) संगीतकार
(ग) नायक
(घ) खलनायक।
उत्तर :
(ख) संगीतकार
प्रश्न 8.
थामस अल्बा एडिसन किस शक्ति से रहित थे?
(क) श्रवण की
(ख) देखने की
(ग) बोलने की
(घ) चलने की।
उत्तर :
(क) श्रवण की
प्रश्न 9.
कुष्ट रोगियों की सेवा किसने की?
(क) विनोबा भावे
(ख) महात्मा गांधी
(ग) बाबा आम्टे
(घ) बाबा साहब अंबेडकर।
उत्तर :
(ग) बाबा आम्टे
![]()
प्रश्न 10.
महाराजा रणजीत सिंह ने किस कारण एक आँख खो दी थी?
(क) चोट के
(ख) चेचक के
(ग) कैंसर के
(घ) तीर लगने से।
उत्तर :
(ख) चेचक के
मन के जीते जीत Summary in Hindi
मन के जीते जीत पाठ का सार
‘मन के जीते जीत’ लेखक डॉ० सुनील बहल द्वारा लिखित है। इसमें लेखक ने मन पर विजय पाने से ही सफलता मिलती है-इसका वर्णन किया है। जीवन में छोटी-बड़ी परेशानियां सबके जीवन में आती हैं। हम उनके आने से निराश हो जाते हैं। सभी के जीवन में मुश्किल घड़ियां आती हैं किन्तु इन पर वही विजय प्राप्त करते हैं जो मुश्किलों के सामने घुटने नहीं टेकते बल्कि उनका साहस के साथ मुकाबला करते हैं।
दुनिया में सामान्य लोगों ने ही नहीं बल्कि विकलांग लोगों ने भी ऐसा साहस दिखाया है, जिसके कारण उनकी विकलांगता उनके सामने झुक गई। त्रेतायुग में अष्टावक्र विकलांग हुए जो आठ जगह से टेढ़े थे। एक बार उन्हें राजा जनक के दरबार में देखकर सब हँसने लगे तो अष्टावक्र ने उन्हें बताया कि गन्ने के टेढ़े-मेढ़े होने से उसकी मिठास कम नहीं होती न फूल की पंखुड़ी टेढ़े होने से उसकी खुशबू खत्म होती है, न नदी की धारा टेढ़ी होने से उसका जल दूषित होता है। यह सुनकर राजा जनक तथा दरबारी बहुत लज्जित हुए और उसकी विदवता के सामने नतमस्तक भी हुए।
हिंदी-साहित्य में भक्तिकाल में सूरदास जो जन्म से ही अन्धे थे। किन्तु उन्होंने श्री कृष्ण की लीलाओं का बहुत ही सजीव वर्णन किया है जो संसार में दुर्लभ है। इसी तरह जायसी भी एक आँख और एक कान से रहित थे। शेरशाह के उपहास उड़ाने पर उन्होंने उनको कहा था कि तुम मुझ पर हँसों अथवा उस ईश्वर पर जिसने मुझे बनाया है। इससे शेरशाह बहुत लज्जित हुए थे। जायसी का महाकाव्य पद्मावत बहुत प्रसिद्ध है। नेत्रहीन एवं गरीब मिल्टन कभी जीवन से निराश नहीं हुए इसीलिए अंग्रेजी साहित्य में उनका अद्वितीय स्थान रहा।
![]()
भारतीय सिनेमा में रवीन्द्र जैन की दृढ़ इच्छा शक्ति, एकाग्रता और आत्म विश्वास के आगे अपनी विकलांगता को भी हरा दिया। वे अद्भुत संगीतकार थे। इन्होंने रामानंद सागर द्वारा प्रसारित ‘रामायण’ में भी संगीत दिया। इसके साथ अलिफ लैला, जय हनुमान, श्री कृष्ण आदि महान् धारावाहिकों में सभी कर्णप्रिय संगीत दिया।
विश्व के महान् आविष्कारक थामस अल्वा एडीसन सुनने की श्रवण शक्ति खो चुके थे। किन्तु वे जीवन से निराश नहीं हुए। उन्होंने अपने साहस के बल पर हजारों आविष्कार किए। बिजली के बल्ब का आविष्कार उनकी बड़ी उपलब्धि है। तीन वर्ष की आयु में नेत्रहीन हो जाने वाले लुई ब्रेल भी अपनी इच्छा शक्ति के बल पर नेत्रहीन स्कूल में पढ़े और अध्यापक बने। उन्होंने अपने अनथक प्रयासों से नेत्रहीनों के किए ब्रेल नामक लिपि का आविष्कार किया जो दुनिया में आज भी प्रयुक्त हो रही है।
महान् समाज सेवी बाबा आम्टे को कौन नहीं जानता। वे भयंकर अस्थि विकलांगता से पीड़ित थे किन्तु फिर भी इन्होंने सारी उम्र कुष्ट रोगियों की सेवा की। इनको समाज सेवा के कारण ही भारत सरकार ने सन् 1971 ई० में पदम्श्री तथा सन् 1986 ई० में पद्मभूषण सम्मान से सम्मानित किया। भारतीय क्रिकेट में भी विकलांग होने के बावजूद स्पिनर चंद्रशेखर ने क्रिकेट में अपनी जगह बनाई। उनका एक हाथ पोलियोग्रस्त था किन्तु वे उसी हाथ से गेंदबाजी करते थे। उन्होंने भारतीय टीम की ओर से 58 टैस्ट मैच तथा 7199 रन देकर 242 विकट लिए। उन्हें अर्जुन पुरस्कार प्रदान किया गया।
भारतीय इतिहास में वीर राणा सांगा, जिन्होंने बचपन में अपनी एक आँख खो दी थी, अपने वीरता बल एवं साहस से दुनिया में अपनी ताकत का लोहा मनवाया। युद्ध में एक पैर और हाथ भी खो दिया पर वे इससे बिल्कुल भी घबराये नहीं। इन्होंने इब्राहिम लोदी जैसे अनेक विरोधियों को हराया।
इसी तरह महाराजा रणजीत सिंह की चेचक के कारण एक आँख खराब थी किन्तु फिर भी उन्होंने उन्नीस वर्ष की आयु में लाहौर पर अधिकार कर लिया था और धीरे-धीरे जम्मू-कश्मीर, अमृतसर, मुलतान, पेशावर आदि क्षेत्रों पर अधिकार कर लिया। उन्हें कुशल प्रबन्ध, वीरता, न्यायप्रियता, दयालुता और दानशीलता के कारण जाना जाता है।
इस प्रकार यदि मनुष्य के दिल में कुछ कर गुजरने की इच्छा हो तो मुसीबतें हार जाती हैं इसलिए हमें अपने आत्म-विश्वास, दृढ़ निश्चय, चित्र की एकाग्रता और अपनी शक्तियों को केंद्रित करके अपने लक्ष्य की ओर आगे बढ़ना चाहिए। यह सत्य है कि ईश्वर भी केवल साहसी लोगों की ही सहायता करते हैं।
![]()
मन के जीते जीत शब्दार्थ :
- हताश = निराश।
- विकलांगता = विकलांग पन।
- विभूतियों = महान् व्यक्तियों।
- अष्टावक्र = आठ वक्र वाला।
- दूषित = खराब।
- विद्वता = ज्ञान, बुद्धि।
- नतमस्तक = सुभगाय।
- नेत्रहीन = अंधा।
- दुर्लभ = कठिन।
- अन्यत्र = दूसरी जगह, कठहार वाले का हार।
- उपहास = मजाक।
- निस्संदेह = वास्तव में।
- अस्थि = हड्डी।
- परितयक्त = त्यागे हुए।
- अनथक = बिना थके।
- तमन्ना = इच्छा।
- ज़ज्बा = साहस।
मन के जीते जीत सप्रसंग व्याख्या
1. बच्चो ! हम जीवन में आने वाली छोटी-छोटी परेशानियों से निराश और हताश हो जाते हैं। हमें अपने चारों ओर अंधकार ही अंधकार दिखाई देता है। कहीं कोई रास्ता दिखाई नहीं देता। हम थक कर बैठ जाते हैं। कभी भाग्य को, कभी अपने आपको तो कभी किसी को कोसने लगते हैं। पर मोचो ! रुकावटें किसके रास्ते में नहीं आती? सभी के जीवन में मुश्किल भरे पल आते हैं किन्तु उन मुश्किलों से पार वे ही जा पाते हैं जो उनके आगे सिर नहीं झुकाते, उनका दृढ़ता से सामना करते हैं। सामान्य व्यक्तियों की तो बात ही छोड़ो, दुनिया में ऐसे विकलांग व्यक्ति भी हुए हैं जिन्होंने अपनी विकलांगता को चुनौती के रूप में लिया और परिणाम यह हुआ कि खुद विकलांगता ने ही उनके अदम्य साहस और दृढ़ निश्चय के आगे घुटने टेक दिये।

प्रसंग-यह गद्यांश लेखक डॉ० सुनील बहल द्वारा रचित ‘मन के जीते जीत’ शीर्षक पाठ से लिया गया है। इसमें लेखक ने बच्चों के जीवन में आने वाली मुसीबतों का डटकर सामना करने की प्रेरणा दी है।
![]()
व्याख्या-लेखक बच्चों को प्रेरणा देते हुए कहता है कि हे बच्चो! हम जीवन में आने वाली छोटी-छोटी परेशानियों एवं कठिनाइयों से निराश एवं हताश हो जाते हैं। हमें अपने चारों तरफ अन्धेरा ही अन्धेरा दिखाई देता है। कहीं भी कोई रास्ता नज़र नहीं आता जिससे हम थक हारकर बैठ जाते हैं। हम कुछ करने की अपेक्षा अपने भाग्य अपने आपको तथा किसी दूसरे को कोसने लगते हैं। परन्तु बच्चों तुम सोच विचार करो कि जीवन में किसके रास्ते में रुकावटें नहीं आतीं।
सभी के मार्ग में बाधाएं, मुसीबतें आती हैं। सभी के जीवन में मुश्किलों से भरे क्षण आते हैं किन्तु उन मुश्किलों पर वे ही लोग विजय प्राप्त कर पाते हैं जो उनके आगे अपना सिर नहीं झुकाते, उनसे हार नहीं मानते बल्कि उनका साहस के साथ मुकाबला करते हैं। सामान्य व्यक्तियों की बात तो छोड़िए दुनिया में ऐसे विकलांग व्यक्ति भी हुए हैं जिन्होंने अपनी विकलांगता को चुनौती के रूप में लिया अर्थात् विकलांग होते हुए भी संघर्ष और परिश्रम किया जिसके परिणाम यह हुआ कि विकलांगता स्वयं ही उनके अटूट साहस और दृढ़ निश्चय के सामने झुक गई।
भावार्थ-बच्चों को जीवन में साहस एवं दृढ़ निश्चय के साथ मुसीबतों का सामना करने की प्रेरणा दी है एवं विकलांगता पर विजय पाने वालों की ओर संकेत है।
2. त्रेता युग में एक विद्वान् हुए जिनका नाम था अष्टावक्र। जब उनका जन्म हुआ तो वे आठ जगह से टेढ़े थे। आठ प्रकार की वक्रता के कारण ही उनका नाम अष्टावक्र पड़ा। एक बार वे राजा जनक के दरबार में गये तो उसके टेढ़े-मेढ़े शरीर को देखकर सभी हँसने लगे। अष्टावक्र ने कहा, “गन्ने के टेढ़े-मेढ़े होने से उसकी मिठास में कमी नहीं आती। फूल की पंखुड़ी के टेढ़े होने से उसकी खुशबू खत्म नहीं हो जाती और नदी की धारा के टेढ़े होने से उसका जल दूषित नहीं हो जाता।” यह सुनकर राजा जनक तथा दरबारी न केवल लज्जित हुए बल्कि अष्टावक्र की विद्वता के सामने नतमस्तक हुए।

प्रसंग-यह गद्यांश लेखक डॉ. सुनील वहल द्वारा रचित ‘मन के जीते जीत’ नामक पाठ से लिया गया है। इसमें लेखक ने त्रेतायुग में अपनी विकलांगता पर विजय पाने वाले विद्वान् अष्टावक्र का चित्रण किया है।
![]()
व्याख्या-लेखक कहता है कि त्रेता युग में अष्टावक्र नामक एक महान् विद्वान् हुआ। वे अपने जन्म के समय से ही आठ जगह से टेढे थे। इसी आठ प्रकार के टेढेपन के कारण ही उनका नाम अष्टावक्र पड़ा था। एक बार वे राजा जनक के दरबार में गए तो उनके टेढ़े-मेढे शरीर को देखकर सभी लोग हँसने लगे।
उन्हें हँसता देखकर अष्टावक्र ने कहा कि गन्ने के टेढ़े-मेढ़े होने से उसकी मिठास में कमी नहीं आती। फूल की पंखुड़ी के टेढ़े होने से उसकी खुशबू खत्म नहीं होती तथा न ही नदी की धारा के टेढ़े होने से उसका जल दूषित हो जाता है। उनके मुख से इस बात को सुनकर राजा जनक तथा सभी दरबारी केवल लज्जित ही नहीं हुए बल्कि अष्टावक्र की विद्वता के सामने नतमस्तक भी हो गए।
भावार्थ-अष्टावक्र के गुणों और विद्वता का उल्लेख किया गया है।
3. भारतीय सिनेमा में प्रसिद्ध संगीतकार रवीन्द्र जैन का महत्त्वपूर्ण स्थान रहा है। बचपन से ही इन्हें न के बराबर दिखाई देता था। आँखों के आप्रेशन के बाद भी इनकी आँखें ठीक नहीं हुईं किन्तु रवीन्द्र जैन की दृढ़ इच्छा शक्ति, एकाग्रता और आत्मविश्वास के आगे विकलांगता की एक न चली। उन्होंने फिल्मों में अद्भुत संगीत दिया। जो आज भी लोगों के मन-मस्तिष्क पर छाया हुआ है। रामानन्द सागर द्वारा टेलीविज़न पर प्रसारित ‘रामायण’ में भी इन्होंने ही संगीत दिया जो बहुत लोकप्रिय हुआ। इसके अतिरिक्त उन्होंने अलिफ लैला, जय हनुमान, श्रीकृष्ण आदि धारावाहिकों में भी कर्णप्रिय संगीत दिया।

प्रसंग-यह पंक्तियाँ डॉ० सुनील बहल द्वारा लिखित ‘मन के जीते जीत’ नामक पाठ से लिया गया है। इसमें लेखक ने सुप्रसिद्ध संगीतकार रवीन्द्र जैन के संघर्ष का वर्णन किया है।
व्याख्या-लेखक कहता है कि भारतीय सिनेमा में प्रसिद्ध संगीतकार रवीन्द्र जैन का महत्त्वपूर्ण स्थान रहा है। बचपन से ही इन्हें न के बराबर दिखाई देता था। इन्होंने अपनी आँखों का आप्रेशन करवाया। इसके बाद इनकी आँखें ठीक ही नहीं हुईं। किन्तु रवीन्द्र जैन की दढ इच्छा शक्ति, एकाग्रता और अपने विश्वास के आगे इनकी विकलांगता हार गई।
अर्थात् इन्होंने अपने आत्मविश्वास के बल से अपनी विकलांगता पर विजय पा ली। इन्होंने फिल्मों में अद्भुत संगीत दिया। जो आज भी लोगों के मन-मस्तिष्क पर छाया हुआ है। इन्होंने रामानंद सागर द्वारा टेलीविज़न पर प्रसारित रामायण में संगीत दिया जो बहुत लोकप्रिय हुआ। इसके अलावा इन्होंने अलिफ लैला, जय हनुमान, श्रीकृष्ण, आदि धारावाहिकों में भी बहुत मधुर संगीत दिया।
![]()
भावार्थ-भारतीय संगीतकार रवीन्द्र जैन की दृढ़ इच्छा शक्ति और आत्म विश्वास को दर्शाया गया है।
4. इस तरह मात्र तीन वर्ष की आयु में नेत्रहीन हो जाने वाले लुई ब्रेल ने भी जीवन में अनेक कष्ट सहे। वे स्वयं दृष्टिहीन लोगों के स्कूल में पढ़े व अध्यापक बने किन्तु उस समय तक नेत्रहीनों के लिए सीखने के लिए कोई बढ़िया तकनीक नहीं थी। अतएव लुई ब्रेल ने अनथक प्रयत्नों के बाद नेत्रहीनों के लिए एक ऐसी लिपि का आविष्कार किया जिससे नेत्रहीन पढ़ने में समर्थ हो सके। इस लिपि को ब्रेल लिपि कहते हैं। यह लिपि कागज़ पर उभरे चिह्न होते हैं जिन्हें स्पर्श कर वे पढ़ते हैं। बेशक यह लिपि दुनिया भर में आज प्रयुक्त हो रही है।

प्रसंग-यह गद्यांश खंड डॉ० सुनील बहल द्वारा रचित ‘मन के जीते जीत ही’ शीर्षक पाठ से लिया गया है। इसमें नेत्रहीन लुई ब्रेल के परिश्रम, साहस एवं आविष्कार को दर्शाया है।
व्याख्या-लेखक कहता है कि लुई ब्रेल केवल तीन वर्ष के आयु में नेत्रहीन हो जाने पर अनेक कष्ट सहन किए। वे अपने आप नेत्रहीन लोगों के स्कूल में पढ़े तथा अध्यापक बने। किन्तु उस समय तक नेत्रहीन लोगों को सीखने के लिए कोई अच्छी तकनीक नहीं थी। इसीलिए लई ब्रेल ने अपने अनथक प्रयासों के बाद, नेत्रहीन लोगों के लिए एक ऐसी लिपि का आविष्कार किया जिससे नेत्रहीन पढ़ने में समर्थ हो सके। इस लिपि को ब्रेल लिपि कहते हैं। यह लिपि कागज़ पर उभरे चिह्न होते हैं, जिन्हें स्पर्श कर वे पढ़ते हैं। यह लिपि सारी दुनिया में आज प्रयोग में लाई जा रही है।
![]()
भावार्थ-लई ब्रेल के प्रयासों तथा ब्रेल लिपि के आविष्कार को प्रयासों में बताया है।
5. भारतीय इतिहास में ऐसे व्यक्तित्व भी हैं जिन्होंने अपनी विकलांगता से कभी हार नहीं मानी अपितु वीरता एवं साहस के बल पर दुनिया में अपनी ताकत का लोहा मनवाया। राणा सांगा ने बचपन में अपनी एक आँख खो दी थी और बाद में युद्धों में एक हाथ और एक पैर को भी इन्होंने खो दिया किन्तु इस विकलांगता का उनकी वीरता और साहस पर कोई असर नहीं पड़ा। बड़े-बड़े शासक उनके नाम से थर-थर काँपते थे। राणा सांगा ने इब्राहिम लोदी जैसे अनेक विरोधियों के दाँत खट्टे किये। इसी तरह महाराजा रणजीत सिंह की चेचक के कारण एक आँख खराब हो गयी थी। किन्तु फिर भी वे निराश नहीं हुए। उन्नीस वर्ष की आयु में उन्होंने लाहौर पर अधिकार कर लिया था। फिर धीरे-धीरे जम्मू कश्मीर, अमृतसर, मुलतान, पेशावर आदि क्षेत्रों पर इन्होंने अधिकार कर लिया। अपने कुशल प्रबन्ध, वीरता, न्यायप्रियता, दयालुता और दानशीलता के कारण महाराज रणजीत सिंह को जाना जाता है।

प्रसंग-यह पंक्तियाँ लेखक डॉ० सुनील बहल द्वारा लिखित है। यह ‘मन के जीते जीत है’ शीर्षिक पाठ से ली गई हैं। इनमें लेखक ने राणा सांगा की वीरता, साहस तथा महाराजा रणजीत सिंह की वीरता और दयालुता को दर्शाया है।
व्याख्या-भारत के इतिहास में ऐसे महान् लोग भी हुए हैं जिन्होंने अपनी विकलांगता से जीवन में कभी हार नहीं मानी अपितु वीरता एवं साहस के बल पर दुनिया में अपनी शक्ति का लोहा मनवाया। राणा सांगा ने बचपन में अपनी एक आँख खो दी थी किन्तु इस विकलांगता का उनकी वीरता और साहस पर कोई प्रभाव नहीं पड़ा। बड़े-बड़े शासक उनके नाम से थर-थर काँपते थे। राणा सांगा ने इब्राहिम लोदी जैसे अनेक विरोधियों को बुरी तरह से हराया था।
इस तरह महाराजा रणजीत सिंह की चेचक के कारण एक आँख खराब हो गई थी किन्तु फिर भी वे निराश नहीं हुए उन्होंने केवल उन्नीस वर्ष की आयु में लाहौर पर अधिकार कर लिया था। इसके बाद धीरे-धीरे जम्मू-कश्मीर, अमृतसर, मुलतान, पेशावर आदि क्षेत्रों पर पुस्तकीय भाग इन्होंने अधिकार कर लिया। उसका प्रबन्ध अत्यंत कुशल था। वे अत्यन्त वीर तथा न्यायप्रिय थे, उनके दयालुता और दानशीलता सभी जलते हैं। इसी कारण उनकी वीरता, न्यायप्रियता, दयालुता एवं दानवीरता के कारण महाराजा रणजीत सिंह को जाना जाता है।
![]()
भावार्थ-राणा सांगा की वीरता एवं साहस को दर्शाया गया है और महाराजा रणजीत सिंह की वीरता, न्यायप्रियता, दानशील और दयालुता का वर्णन है।
6. अतएव बच्चो ! यदि दिल में कुछ कर गुजरने की तमन्ना और जज्बा हो तो तमाम मुसीबतों को आखिरकार घुटने टेकने ही पड़ते हैं। अब आप ही बताइये यदि इन विभूतियों ने जीवन के संघर्ष में अपनी हार मान ली होती तो क्या वे आज दुनिया के लिए प्रेरणा स्रोत बन पाते? आइए, उठिये, अपने आत्मविश्वास, दृढ़निश्चय, चित्त की एकाग्रता और अपनी शक्तियों को केन्द्रित करें और अपने लक्ष्य की ओर बढ़ें। कहा भी है, “भाग्य संवरता नहीं संवारना पड़ता है और भी कहा गया है, “ईश्वर भी उन्हीं की सहायता करते हैं जो अपनी सहायता अपने आप करते हैं।”

प्रसंग-यह गद्यांश लेखक डॉ० सुनील बहल द्वारा लिखित है। यह ‘मन के जीते जीत है’ शीर्षक पाठ से लिया गया है। इसमें लेखक ने बच्चों को साहस, आत्मविश्वास एवं दृढ़ निश्चय से जीवन में आगे बढ़ने की प्रेरणा दी है।
व्याख्या-लेखक बच्चों को प्रेरणा देकर कहता है कि हे बच्चो! यदि दिल में कुछ करने की इच्छा हो और हिम्मत एवं साहस हो तो सभी मुसीबतें अवश्य खत्म हो जाती हैं। अब आप ही बताइए कि यदि सूरदास, जायसी, रवीन्द्र जैन, चन्द्रशेखर, राणा सांगा, महाराजा रणजीत सिंह, लुई ब्रेल आदि महान् विद्वानों ने जीवन के संघर्ष में अपनी हार मान ली होती तो क्या वे आज इस संसार के प्ररेणा स्रोत बन पाते अर्थात् नहीं।
वे सभी विकलांग होते हुए भी संघर्ष करते रहे और विजयी हुए इसीलिए दुनिया उनसे प्रेरणा ले रही है। इसलिए आओ फिर से अपने आत्मविश्वास, दृढ़ निश्चय, मन की एकाग्रता और शक्तियों को केन्द्रित करें और अपने लक्ष्य की तरफ बढ़े। यहाँ सच ही कहा गया है कि भाग्य अपने आप नहीं संवरता बल्कि उसे तो संवारना पड़ता है। ईश्वर भी संसार के केवल उन्हीं लोगों की सहायता करते हैं जो अपनी सहायता स्वयं करते हैं। इसलिए हम साहस आत्मविश्वास परिश्रम से आगे बढ़ें।
![]()
भावार्थ-सूरदास, मिल्टन, जायसी, अष्टावक्र, महाराजा रणजीत सिंह जैसी विभूतियों से प्रेरणा लेने को कहा है।