Punjab State Board PSEB 10th Class Physical Education Book Solutions ਗਤਕਾ (Gatka) Game Rules.
ਗਤਕਾ (Gatka) Game Rules – PSEB 10th Class Physical Education
ਯਾਦ ਰੱਖਣ ਦਾ ਹੀਲਾ
(Points to Remember)
- ਗਤਕੇ ਦਾ ਪਲੇਟ ਫਾਰਮ ਦਾ ਆਕਾਰ = ਗੋਲ
- ਪਲੇਟ ਫਾਰਮ ਦਾ ਘੇਰਾ = 30″, 20cm
- ਗਤਕੇ ਦੀ ਲੰਬਾਈ = 3′.3″, 100cm
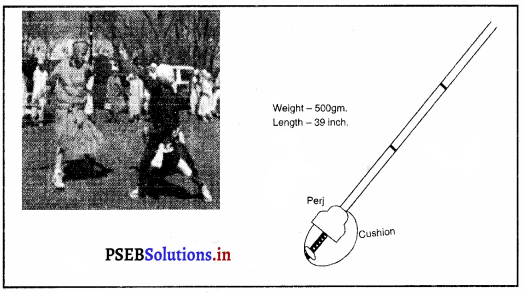
- ਗਤਕੇ ਦਾ ਭਾਰ = 500gm
- ਗਤਕੇ ਦੀ ਬਨਾਵਟ = ਬੈਂਤ
- ਗਤਕੇ ਦੀ ਮੋਟਾਈ = 1/2 to 3/4, 2cm to 3cm
- ਬਾਉਟ ਦਾ ਸਮਾਂ = 3 ਮਿੰਟ (11/2,1/2 ਮਿੰਟ ਦੇ ਦੋ ਹਾਫ਼)
- ਖਿਡਾਰੀ ਦੀ ਪੌਸ਼ਾਕ = ਜਰਸੀ ਜਾਂ ਕਮੀਜ਼, ਸਿਰ ਤੇ ਪਟਕਾ ਜ਼ਰੂਰੀ ਹੈ |
- ਅਧਿਕਾਰੀ = 1 ਰੈਫਰੀ, 2 ਤਕਨੀਕ ਅਧਿਕਾਰੀ, 1 ਜੱਜ, 1 ਸਕੋਰਰ, 1 ਟਾਈਮ ਕੀਪਰ
ਖੇਡ ਸੰਬੰਧੀ ਮਹੱਤਵਪੂਰਨ ਜਾਣਕਾਰੀ
- ਗਤਕੇ ਵਿਚ 7 ਖਿਡਾਰੀ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿਚੋਂ 5 ਖੇਡਦੇ ਹਨ ਅਤੇ ਦੋ ਖਿਡਾਰੀ ਬਦਲਵੇਂ ਹੁੰਦੇ ਹਨ |
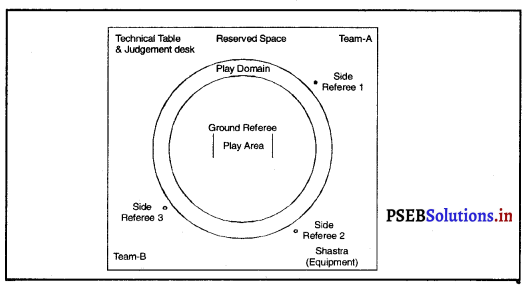
- ਗਤਕੇ ਦਾ ਪਲੇਟਫਾਰਮ ਗੋਲ ਅਤੇ ਇਸਦਾ ਮਾਪ 71/2 ਮੀਟਰ ਰੇਡੀਅਸ ਹੁੰਦਾ ਹੈ ।
- ਗਤਕੇ ਦੀ ਲੰਬਾਈ ਮੁੱਠ ਤੋਂ ਤਿੰਨ ਫੁੱਟ ਤਿੰਨ ਇੰਚ ਹੁੰਦੀ ਹੈ ।
- ਗਤਕੇ ਵਿਚ ਬਾਉਟ ਦਾ ਸਮਾਂ ਤਿੰਨ ਮਿੰਟ ਹੁੰਦਾ ਹੈ ।
- ਗਤਕੇ ਦੀ ਖੇਡ ਵਿਚ ਤਿੰਨ ਜੱਜ, ਇਕ ਰੈਫਰੀ ਅਤੇ ਇਸ ਟਾਈਮ ਕੀਪਰ ਹੁੰਦਾ ਹੈ ।
ਪਲੇਟ ਫਾਰਮ-
ਗਤਕੇ ਦਾ ਪਲੇਟਫਾਰਮ ਗੋਲ ਹੁੰਦਾ ਹੈ ਜਿਸ ਦਾ ਸਾਈਜ਼ 15 ਮੀਟਰ ਹੁੰਦਾ ਹੈ ।
ਪੋਸ਼ਾਕ-
ਪ੍ਰਤੀਯੋਗੀ ਇਕ ਜਰਸੀ ਜਾਂ ਕਮੀਜ਼ ਪਾ ਸਕਦਾ ਹੈ ਪਰ ਸਿਰ ‘ਤੇ ਪਟਕਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ।
ਗਤਕੇ ਦਾ ਸਾਈਜ਼-
ਗਤਕਾ ਬੈਂਤ ਦਾ ਹੁੰਦਾ ਹੈ ਜਿਸਦੇ ਮੁੱਢ ਤੇ ਤਿੰਨ ਫੁੱਟ ਲੰਬੀ ਬੈਂਤ ਦੀ ਛੜ ਲੱਗੀ ਹੁੰਦੀ ਹੈ ।
ਮਿਆਦਾ-
ਸਾਰੇ ਮੁਕਾਬਲਿਆਂ ਲਈ ਇਸ ਬਾਊਟ ਦੀ ਮਿਆਦ ਪੰਜ ਮਿੰਟ ਹੁੰਦੀ ਹੈ ।
![]()
ਡਰਾਅ, ਬਾਈ, ਵਾਕ ਓਵਰ
(Draw, Byes And Walk Over)
1. ਸਾਰੇ ਮੁਕਾਬਲਿਆ ਲਈ ਡਰਾਅ ਕੱਢਣ ਤੋਂ ਪਹਿਲਾਂ ਬਾਉਟ ਦੇ ਨਾਂ A, B, C, D, E ਲਏ ਜਾਂਦੇ ਹਨ ।
2. ਗਤਕੇ ਵਿਚ A ਬਾਊਟ ਦਾ ਖਿਡਾਰੀ ਦੂਸਰੀ ਟੀਮ ਦੇ A ਬਾਊਟ ਦੇ ਖਿਡਾਰੀ ਨਾਲ ਹੀ ਖੇਡੇਗਾ ਅਤੇ B ਵਾਲਾ B ਨਾਲ ।
3. ਉਹ ਪ੍ਰਤੀਯੋਗਤਾਵਾਂ ਜਿਨ੍ਹਾਂ ਵਿਚ ਚਾਰ ਤੋਂ ਵੱਧ ਪ੍ਰਤੀਯੋਗੀ ਹੋਣ ਪਹਿਲੀ ਸੀਰੀਜ਼ ਵਿਚ ਕਾਫ਼ੀ ਸਾਰੀਆਂ ਬਾਈਆਂ ਕੱਢੀਆਂ ਜਾਣਗੀਆਂ ਤਾਂਕਿ ਦੁਜੀ ਸੀਰੀਜ ਵਿਚ ਪ੍ਰਤੀਯੋਗੀਆਂ ਦੀ ਸੰਖਿਆ ਘੱਟ ਰਹਿ ਜਾਵੇ ।
4. ਪਹਿਲੀ ਸੀਰੀਜ਼ ਵਿਚ ਜਿਹੜੇ ਖਿਡਾਰੀ ਬਾਈ ਵਿਚ ਆਉਂਦੇ ਹਨ, ਉਹ ਦੂਜੀ ਸੀਰੀਜ਼ ਵਿਚ ਪਹਿਲਾਂ ਗਤਕਾ ਖੇਲਣਗੇ ਜੇਕਰ ਬਾਈਆ ਦੀ ਸੰਖਿਆ ਵਿਖਮ ਹੋਵੇ, ਤਾਂ ਅਖੀਰਲੀ ਬਾਈ ਦਾ ਖਿਡਾਰੀ ਦੂਸਰੀ ਸੀਰੀਜ਼ ਵਿਚ ਪਹਿਲੇ ਮੁਕਾਬਲੇ ਦੇ ਜੇਤੂ ਨਾਲ ਮੁਕਾਬਲਾ ਕਰੇਗਾ ।
5. ਕੋਈ ਵੀ ਪ੍ਰਤੀਯੋਗੀ ਪਹਿਲੀ ਸੀਰੀਜ਼ ਵਿਚ ਬਾਈ ਅਤੇ ਦੂਜੀ ਸੀਰੀਜ਼ ਵਿਚ ਵਾਕ ਓਵਰ ਨਹੀਂ ਲੈ ਸਕਦਾ ਨਾ ਹੀ ਦੋ ਲਗਾਤਾਰ ਵਾਕ ਓਵਰ ਲੈ ਸਕਦਾ ।
ਪ੍ਰਸ਼ਨ 1.
ਗਤਕੇ ਵਿਚ ਸਾਰਣੀ-ਬਾਉਟ ਤੋਂ ਬਾਈਆਂ ਕਿਵੇਂ ਕੱਢੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਸਾਰਣੀ-ਬਾਉਟ ਤੋਂ ਬਾਈਆਂ ਕੱਢਣਾ ।
| ਐਂਟਰੀਆਂ ਦੀ ਸੰਖਿਆ | ਬਾਊਟ | ਬਾਈ |
| 5 | 1 | 3 |
| 6 | 2 | 2 |
| 7 | 3 | 1 |
| 8 | 4 | – |
| 9 | 1 | 7 |
| 10 | 2 | 6 |
| 11 | 3 | 5 |
| 12 | 4 | 4 |
| 13 | 5 | 3 |
| 14 | 6 | 2 |
| 15 | 7 | 1 |
| 16 | 8 | – |
| 17 | 1 | 15 |
| 18 | 2 | 14 |
| 19 | 3 | 13 |
| 20 | 4 | 12 |
ਗਤਕੇ ਵਿਚ ਮੁਕਾਬਲੇ
ਪ੍ਰਤੀਯੋਗੀਆਂ ਦੀ ਸੀਮਾ (Limitation of Competitors) – ਕਿਸੇ ਵੀ ਪ੍ਰਤੀਯੋਗਤਾ ਵਿਚ ਪੰਜ ਪ੍ਰਤੀਯੋਗੀਆਂ ਨੂੰ ਭਾਗ ਲੈਣ ਦੀ ਆਗਿਆ ਹੈ ।
ਨਵਾਂ ਡਰਾਅ (Fresh, draw) – ਜੇਕਰ ਕਿਸੇ ਇੱਕੋ ਹੀ ਸਕੂਲ/ਕਾਲਜ ਜਾਂ ਕਲੱਬ ਦੇ ਦੋ ਮੈਬਰਾਂ ਦਾ ਪਹਿਲੀ ਸੀਰੀਜ਼ ਵਿਚ ਡਰਾਅ ਨਿੱਕਲ ਜਾਵੇ ਅਤੇ ਉਹਨਾਂ ਵਿਚੋਂ ਇਕ-ਦੂਜੇ ਦੇ ਹੱਕ ਵਿਚ ਪ੍ਰਤੀਯੋਗਤਾ ਚੋਂ ਨਿਕਲਣਾ ਚਾਹੇ ਤਾਂ ਡਰਾਅ ਨਵਾਂ ਕੱਢਿਆ ਜਾਵੇਗਾ ।
ਵਾਪਸੀ (withdrawal) – ਡਰਾਅ ਕੱਢੇ ਜਾਣ ਤੋਂ ਬਾਅਦ ਜੇਕਰ ਕੋਈ ਪ੍ਰਤੀਯੋਗੀ ਬਿਨਾਂ ਕਿਸੇ ਕਾਰਨ ਤੋਂ ਪ੍ਰਤੀਯੋਗਿਤਾ ‘ਚੋਂ ਹਟਣਾ ਚਾਹੇ, ਤਾਂ ਅਧਿਕਾਰੀ ਪ੍ਰਬੰਧਕਾਂ ਨੂੰ ਇਸ ਦੀ ਸੂਚਨਾ ਦੇਵੇਗਾ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
ਗਤਕੇ ਵਿਚ ਸਕੋਰਿੰਗ ਕਿਵੇਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
- ਗਤਕੇ ਦਾ ਖਿਡਾਰੀ ਆਪਣੇ ਵਿਰੋਧੀ ਨੂੰ ਗਤਕੇ ਨਾਲ ਜਿੰਨੀ ਵਾਰ ਛੂਹ ਲਵੇਗਾ ਉਸ ਨੂੰ ਉੱਨੇ ਹੀ ਅੰਕ ਮਿਲਣਗੇ ਸਿਰ ਤੋਂ ਛੂਹਣ ਦੇ ਦੋ ਅੰਕ ਅਤੇ ਬਾਕੀ ਇਕ ਅੰਕ ਮਿਲੇਗਾ ।
- ਜੇਕਰ ਬਾਊਟ ਦੇ ਅੰਤ ਵਿਚ ਦੋਹਾਂ ਖਿਡਾਰੀਆਂ ਨੂੰ ਮਿਲੇ ਅੰਕ ਬਰਾਬਰ ਹੋਣ, ਤਾਂ ਜਿਸ ਖਿਡਾਰੀ ਨੇ ਸਿਰ ਨੂੰ ਜ਼ਿਆਦਾ ਵਾਰ ਛੂਹਿਆ ਹੋਵੇ, ਉਸ ਨੂੰ ਜੇਤੂ ਮੰਨਿਆ ਜਾਵੇਗਾ । ਜੇਕਰ ਸਿਰ ਨੂੰ ਛੂਹਣ ਦੇ ਅੰਕ ਵੀ ਬਰਾਬਰ ਹੋਣ, ਤਾਂ ਜੱਜ ਆਪਣਾ ਫੈਸਲਾ ਉਸ ਖਿਡਾਰੀ ਦੇ ਪੱਖ ਵਿਚ ਦੇਵੇਗਾ ਜਿਸ ਨੇ ਚੰਗੀ ਸੁਰੱਖਿਆ (Defence) ਦਾ ਪ੍ਰਦਰਸ਼ਨ ਕੀਤਾ ਹੋਵੇ ।
ਬਾਊਟ ਰੋਕਣਾ (Stopping the bout)-
- ਜੇਕਰ ਰੈਫਰੀ ਦੇ ਵਿਚਾਰ ਅਨੁਸਾਰ ਖਿਡਾਰੀ ਚੋਟ ਲੱਗਣ ਕਰਕੇ ਖੇਡ ਜਾਰੀ ਨਹੀਂ ਰੱਖ ਸਕਦਾ ਜਾਂ ਉਹ ਬਾਉਟ ਨੂੰ ਬੰਦ ਕਰ ਦਿੰਦਾ ਹੈ, ਤਾਂ ਉਸ ਦੇ ਵਿਰੋਧੀ ਨੂੰ ਜੇਤੂ ਕਰਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
- ਰੈਫਰੀ ਨੂੰ ਬਾਉਟ ਰੋਕਣ ਦਾ ਅਧਿਕਾਰ ਹੈ ।
- ਜੇਕਰ ਕੋਈ ਖਿਡਾਰੀ ਸਮੇਂ ਸਿਰ ਬਾਊਟ ਕਰਨ ਵਿਚ ਅਸਫਲ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ” ਬਾਊਟ ਹਾਰਿਆ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
ਸੰਕਿਤ ਫਾਉਲ (Suspected foul) – ਜੇਕਰ ਰੈਫਰੀ ਨੂੰ ਫਾਉਲ ਦਾ ਸ਼ੱਕ ਹੋਵੇ, ਜਿਸ ਨੂੰ ਉਸ ਨੇ ਆਪ ਸਾਫ਼ ਨਹੀਂ ਦੇਖਿਆ, ਉਹ ਜੱਜਾਂ ਦੀ ਸਲਾਹ ਵੀ ਲੈ ਸਕਦਾ ਹੈ ਅਤੇ ਉਸ ਦੇ ਅਨੁਸਾਰ ਆਪਣਾ ਫੈਸਲਾ ਦੇ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਗਤਕੇ ਦੇ ਕੋਈ ਦਸ ਫਾਉਲ ਲਿਖੋ ।
ਉੱਤਰ-
ਫਾਊਲ (Foul)-
- ਕੂਹਣੀ ਨਾਲ ਮਾਰਨਾ
- ਗਰਦਨ ਜਾਂ ਸਿਰ ਦੇ ਪਿੱਛੇ ਜਾਣ-ਬੁੱਝ ਕੇ ਚੋਟ ਕਰਨਾ |
- ਹੇਠਾਂ ਡਿੱਗੇ ਪ੍ਰਤੀਯੋਗੀ ਨੂੰ ਮਾਰਨਾ
- ਪਕੜਨਾ
- ਸਿਰ ਦੀ ਨਾਜਾਇਜ ਵਰਤੋਂ ਕਰਨਾ
- ਸਿਰ ਜਾਂ ਸਰੀਰ ਦੇ ਭਾਰ ਲੇਟਣਾ
- ਰੀਫੰਗ
- ਮੋਢੇ ਮਾਰਨਾ ।
- ਕੁਸ਼ਤੀ ਕਰਨਾ
- ਲਗਾਤਾਰ ਸਿਰ ਢੱਕ ਕੇ ਰੱਖਣਾ । ‘




